Factor completely or state that the polynomial is prime.2x^4-2
Answers
2(x²+1)(x+1)(x-1)
1) Let's examine that polynomial to check whether that polynomial can be factored or not.
\(2x^4-2\)2) Examining we can see that the coefficient of the x-term (2) and the constant (2), are the same. So we can find the GCD, between 2,2 and write it as a factor.
GCD (2, 2) = 2
Now we'll divide every term by the GCD, and write it inside the parentheses just like this
\(\begin{gathered} 2x^4-2 \\ \frac{2x^4}{2}=x^4 \\ \frac{-2}{2}=-1 \\ \\ 2(x^4-1)^{} \end{gathered}\)2.2) Now let's proceed with the factorization of the binomial x^4-1
Remembering that (a+n)(a-b)=a²-b²
Notice that we are dealing with a 4th-degree polynomial, so we can write it as:
So we can rewrite it as
\(2(x^4-1)=2(x^2+1)(x^2-1^2)\text{ =}2(x^2+1)(x+1)(x-1)\)3) So our polynomial is not prime, for it can be reduced. And it can be written as 2(x²+1)(x+1)(x-1) in its simplest form.
Related Questions
Which of the following is the equation of a line with a slope of -5/9
Answers
Answer:
Please help me important question in image
Please help me important question in image
Please help me important question in image
Step-by-step explanation:
Please help me important question Please help me important question in image
in image
Please help me iPlease help me important question in image
Please help me important question in image
mportant question in image
Please help me important question in image
What is the length of BC?

Answers
Answer: BC = 24
Step-by-step explanation:
Given:
AB = x+33
AC = 3x - 15
BC = x
<B = <C
Solution:
Because <B = <C, you can say the corresponding sides AB and AC are equal as well
AB = AC
x + 33 = 3x -15
48 = 2x
x = 24
Since x = BC
BC = x
BC = 24
PLS I NEED HELP!!! What is the equivalent Celsius temperature to 120 degrees Fahrenheit? Rearrange and use the formula F = (9/5)C + 32. ( AND PLS PUT THE WORK U DID HERE)
Answers
Answer:
49.8 degrees celcius
Step-by-step explanation:
solve the following inequality, algebra 1.
will give brainliest answer !!

Answers
Step-by-step explanation:
Given:
\( \cfrac{m - 8}{2} < 2 \: \: \: \: \: ...1\)
\( \cfrac{3m + 1}2 > - 1 \: \: \: \: \: ...2\)
Inequality 1:
Simplify:
1/2 m - 4 < 2Add 4 to both sides:
1/2 m - 4 + 4 < 2+41/2 m < 6Multiply both sides by 2:
1/2 m * 2 < 6*2 m < 12Hence,m < 8
Inequality 2:
\( \cfrac{3m + 1}2 > - 1\)
This inequality can't be solved because the absolute values can't be less than 0,and can't be negative.
No solutions.ABCD is a parallelogram.
The coordinates of point A are (2,5)
x = (4,0) and y = (5,12)
Find the coordinates of points B and C.

Answers
Answer:
B(6, 5), C(1, -7)
Step-by-step explanation:
A(2, 5)
From A to B, there is translation x, (4, 0).
Add 4 to A's x-coordinate, and add 0 to A's y-coordinate.
B(2 + 4, 5 + 0) = B(6, 5)
From C to B there is the translation y, (5, 12).
Since we are going from B to C, we undo translation y.
The translation from B to C is (-5, -12).
C(6 - 5, 5 - 12) = C(1, -7)
Write the following number in standard decimal form.
five and two hundredths
Answers
Step-by-step explanation:
5.02 is the answer as five and two hundredths
A certain element decays at a constant rate of 6% per year. If you start with 20 grams of the element, how long will it take before there are only four grams left?
Answers
Answer:
26.0 years
Step-by-step explanation:
It will take approximately 16.79 years (to the nearest hundredth) for the initial mass of 20 grams to decay to four grams, given a constant decay rate of 6% per year.
To determine how long it will take for the 20 grams of the element to decay to four grams, we need to calculate the time using the given decay rate.
Given:
Initial mass (M₀) = 20 grams
Decay rate: 6% per year
Let's set up an equation to represent the decay of the element:
M(t) = M₀ * (1 - r)^t
Here, M(t) represents the mass at time t in years, M₀ is the initial mass, r is the decay rate (expressed as a decimal), and t is the time in years.
We want to find the value of t when M(t) = 4 grams:
\(4 = 20 * (1 - 0.06)^t\)
Dividing both sides by 20:
\(0.2 = (1 - 0.06)^t\)
Taking the natural logarithm of both sides:
\(ln(0.2) = ln[(1 - 0.06)^t]\)
Using logarithmic properties, we can simplify further:
\(ln(0.2) = t * ln(1 - 0.06)\)
Now, we can solve for t by dividing both sides of the equation by ln(1 - 0.06):
t =\(ln(0.2) / ln(1 - 0.06)\)
Using a calculator, we find:
t ≈ 16.79 years
Therefore, it will take approximately 16.79 years (to the nearest hundredth) for the initial mass of 20 grams to decay to four grams, given a constant decay rate of 6% per year.
For more such questions on constant decay.
https://brainly.com/question/31314266
#SPJ8
The temperature in a hotel is 21 °C.
The temperature in the hotel is 26,7°C warmer than at the top of the mountain.
The temperature at the top of the mountain is 3.2°C colder than at the bottom of the mountain.
Work out the temperature at the bottom of the mountain.
Answers
The temperature at the bottom of the mountain is 50.9 °C.
Let's work through the given information step by step to find the temperature at the bottom of the mountain.
The temperature in the hotel is 21 °C.
The temperature in the hotel is 26.7 °C warmer than at the top of the mountain.
Let's denote the temperature at the top of the mountain as T_top.
So, the temperature in the hotel can be expressed as T_top + 26.7 °C.
The temperature at the top of the mountain is 3.2 °C colder than at the bottom of the mountain.
Let's denote the temperature at the bottom of the mountain as T_bottom.
So, the temperature at the top of the mountain can be expressed as T_bottom - 3.2 °C.
Now, let's combine the information we have:
T_top + 26.7 °C = T_bottom - 3.2 °C
To find the temperature at the bottom of the mountain (T_bottom), we need to isolate it on one side of the equation. Let's do the calculations:
T_bottom = T_top + 26.7 °C + 3.2 °C
T_bottom = T_top + 29.9 °C
Since we know that the temperature in the hotel is 21 °C, we can substitute T_top with 21 °C:
T_bottom = 21 °C + 29.9 °C
T_bottom = 50.9 °C
Therefore, the temperature at the bottom of the mountain is 50.9 °C.
for such more question on temperature
https://brainly.com/question/14820864
#SPJ8
A right triangle has a hypotenuse with a length 12 and a leg with
length 5. How long is the triangle's other leg?
Answers
Answer:
13
Step-by-step explanation:
pythagorean theorum
a^2+b^2=c^2
12^2+5^2=c^2
144+25=c^2
c^2=169
c=13
The length of the triangle's other leg is approximately 10.908.
What is a triangle?A triangle is a 2-D figure with three sides and three angles.
The sum of the angles is 180 degrees.
We can have an obtuse triangle, an acute triangle, or a right triangle.
We have,
We can use the Pythagorean theorem to solve for the length of the other leg of the right triangle.
The Pythagorean theorem states that for any right triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides (the legs).
That is, for a right triangle with legs a and b and hypotenuse c:
c² = a² + b²
In this case,
We know that the hypotenuse has a length of 12 and one of the legs has a length of 5.
Let's denote the length of the other leg as "x".
So we can set up the equation:
12² = 5² + x²
Simplifying, we get:
144 = 25 + x^2
Subtracting 25 from both sides, we get:
119 = x²
Taking the square root of both sides, we get:
x ≈ 10.908
Therefore,
The length of the triangle's other leg is approximately 10.908.
Learn more about triangles here:
https://brainly.com/question/25950519
#SPJ7
a convex mirror, like the passenger-side rearview mirror on a car, has a focal length of -2.8 m. an object is 5.6 m from the mirror.
Answers
The image's distance from the mirror is -1.87, by using the mirror equation.
Note:- Although the question is missing, I believe the issue is asking where the image is located.
To find the solution to the problem, the mirror equation can be used:
Mirror equation = \(\frac{1}{f}+\frac{1}{d_{o} }+\frac{1}{d_{i} }\)
Where,
f = mirror's focal length
\(d_{o}\) = object's distance from the mirror
\(d_{i}\) = image's distance from the mirror
The focal length is assumed to be negative for a convex mirror in our problem.
f = -2.8 m
The object's distance (do) = 5.6m
By using the mirror equation, the image's distance from the mirror can be determined
\(\frac{1}{f}+\frac{1}{d_{o} }+\frac{1}{d_{i} }\)
i.e, \(\frac{1}{d_{i} } = \frac{1}{f} -\frac{1}{d_{o} }\)
= \(-\frac{1}{2.8} -\frac{1}{5.6}\) = \(-\frac{3}{5.6}\)
= - 0.5357
\(d_{i} =\) \(-\frac{5.6}{3}\)
= -1.87 m
The virtual nature of the image is indicated by the negative sign (located behind the mirror)
To know more about Convex mirror visit here:
https://brainly.com/question/27518252
#SPJ4
Which of the following is a true statement of the figure?
An image of a triangle ABC. The angle bisector of angle B is ray BD. Point D lies on side AC.
Question 1 options:
A
D
D
C
=
D
C
C
B
A
C
A
B
=
D
B
D
C
A
D
D
C
=
A
B
C
B
B
C
B
A
=
D
C
C
B
Answers
Angle ∠EBD is congruent to angle ∠DBA. Option D is the true statement.
What is an angle bisector?An angle bisector is the line segment that bisects the angle into two equal halves.
Orientation of the one line with respect to the horizontal or other respective line is known as a measure of orientation and this measure is known as the angle.
Here,
Ray BE is a bisector of angle CBA,
∠CBE = ∠EBA = 60°
∠EBD = ∠EBA - ∠DBA
∠EBD = 60 - 30 = 30
So,
∠EBD = ∠DBA [DB becomes angle bisector of angle EBA]
Thus, ∠EBD is congruent with ∠DBA is the only correct answer among the option.
Learn more about True Statement at:
https://brainly.com/question/30414310
#SPJ1
Full Question:
Although part of your question is missing, you might be referring to this full question:
Which of the following statements is true if ray BE is a bisector of angle CBA?
A. Ray BD is a bisector of angle CBA.
B. ∠EBD is congruent to ∠CBE.
C. Ray BE is a bisector of angle ABE.
D. ∠EBD is congruent to ∠DBA.

Một hộp thuốc có 5 ống thuốc tốt và 3 ống kém chất lượng. Chọn ngẫu
nhiên lần lượt không trả lại 2 ống. Tính xác suất ñể:
a/ Cả hai ống ñược chọn ñều tốt.
b/ Chỉ ống ñược chọn ra ñầu tiên là tốt.
c/ trong hai ống có ít nhất một ống thuốc tốt.
Answers
Answer:
Step-by-step explanation:
a) Gọi A là biến cố cả 2 ống đã chọn đều tốt. Ta có:
P(A)=A25A28=2056≈0,36.
b) Gọi B là biến cố ống thuốc chọn đầu tiên là tốt.
P(B)=C15.C13A28=1556≈0,27.
c) Gọi C là biến cố 2 ống chọn được có ít nhất một ống thuốc tốt.
P(C)=1−P(C¯¯¯¯)=1−A23A28=5056≈0,89
According to a Pew Research Center report from 2012, the average commute time to work in California is 27.5 minutes. To investigate whether the small city she lives in has a different average, a California high school student surveys 45 people she knows (her teachers, her parents, and their friends and co-workers) and finds the average commute time for this sample to be 24.33 minutes with a standard deviation of 9.53 minutes. The data are not too skewed. The null and alternative hypotheses of her study are: H0 : µ = 27.5 versus Ha : µ 6= 27.5
Required:
a. Identify the observational units for this study.
b. Identify the variable of interest and state whether it is categorical or quantitative.
c. Identify (in words and using an appropriate symbol) the parameter of interest
d. Use the 2SD approach to find a 95% confidence interval for the parameter.
e. Interpret the interval from part d. in context.
Answers
Suppose that the relationship between the tax rate t on imported shoes and the total sales S (in millions of dollars) is given by the function below. Find the tax rate t that maximizes revenue for the government. (Round your answer to three decimal places.)
Answers
The given function for the sales of \(S(t) = 7 - 6 \cdot \sqrt[3]{t} \), gives the tax rate that maximizes government revenue as t = 343/512
What is a government tax rate?The tax rate is the percentage of an amount that is paid to the government as tax.
The given function is presented as follows;
\(S(t) = 7 - 6 \cdot \sqrt[3]{t} \)
Where;
t = The tax rate on imported shoes
S = The total sales
Taking the total sales as contributing to the government revenue, R(t), we have;
Revenue = R(t)
Which gives;
\(R(t) = t \times (7 - 6 \cdot {t}^{ \frac{1}{3} }) \)
At the maximum total sales, we have;
\( \frac{dR(t)}{dt} = \frac{d t \times\left(7 - 6 \cdot {t}^{ \frac{1}{3} } \right) }{dt} = 0 \)
\(\frac{d t \times\left(7 - 6 \cdot {t}^{ \frac{1}{3} } \right) }{dt} = 7- 8 \cdot \sqrt[3]{t} = 0\)
Which gives;
At maximum revenue, t = (7/8)³
t ≈ 0.669921875
The tax rate that maximizes the government revenue is t = 343/512Learn more about government tax rate here:
https://brainly.com/question/9479161
#SPJ1
School starts in 45 minutes and you live 13 miles from school. What average speed (in miles per hour) would allow you to arrive at school on tim
Answers
Answer:
8.2 minutes
So 13 miles would take you roug.hly 8.2 minutes... so going the average speed limit would get you there very
Step-by-step explanation:
One side of a rectangle is 4 m longer than four times another side. The area of the rectangle is 224 m².
Find the length of the shorter side.
m
Answers
Let the another side be x m.
Therefore, the longer side = (4 + 4x) m.
Now,
\({\sf{→x \times (4 + 4x) = 224 \\ →4x + 4x {}^{2} - 224 = 0 \\→ x {}^{2} + x - 56 = 0 \\ →x {}^{2} + 8x - 7x - 56 = 0 \\ →x(x + 8) - 7(x + 8) = 0 \\ →(x - 7)(x +8 ) = 0 \\ →x = 7 \: or \: x = - 8 \\ \\ length \: cannot \: be \: negative \\ possible \: solution \: (x) = 7}}\)
Length of shorter side = x = 7 metres.
\({\sf{answer\: \\ss}}\)
Select the correct months.
The balance of Jim's account on the first day of the month for the first six months of 2013 is given. Identify the months when the balance was
less than the balance in January.
Please answer.

Answers
Answer:
June I got u bro it was easy but there u got
Answer:
june,april,march
Step-by-step explanation:
yeeeeeeeeeeeeeeee i <3 waaaaaaaaafuls
Which of these numbers are perfect squares or perfect cubes? Select the THREE answers that apply. 8 16 32/ 64 128 6 Omestian 12
Answers
Answer:
8, 16, 64
Step-by-step explanation:
8 = 2^3 . . . a perfect cube
16 = 4^2 . . . a perfect square
32 = 2^5 . . . neither a cube nor a square
64 = 2^6 = 4^3 = 8^2 . . . both a perfect cube and a perfect square
128 = 2^7 . . . neither a cube nor a square
Angus earns $8.80 an hour at his Saturday job and $7.50 per hour at his after school job. Last week he earned a total of $127.80. The hours he worked after school were four hours more than he worked on Saturday. How many hours did he work on Saturday?
Answers
Based on equations, Angus worked 6 hours on Saturday and 10 hours at his after-school job last week earning a total of $127.80.
How the hours are determined:The hourly rate at Angus' Saturday job = $8.80
The hourly rate at Angus' after-school job = $7.50
The total earnings last week = $127.80
Let the hours Angus worked at Saturday job = x
Let the hours Angus worked after-school = 4 + x
The total hours worked = x + x + 4
2x + 4
Equations:The total earnings last week 127.80 = 8.8x + 7.5x + 4 (7.5)
127.80 = 8.8x + 7.5x + 30
127.8 - 30 = 16.3x
Hours worked at Saturday Job:x = 6 hours
Hours worked at After-School Job:x + 4 = 10 hours
2x + 4 = 16 (12 + 4)
Check:
Earnings at Saturday job = $52.80 ($8.80 x 6)
Earnings at after-school job = $75.00 ($7.50 x 10)
Total earnings = $127.80
Learn more about equations at https://brainly.com/question/2972832.
#SPJ1
Problem of the week, provide step-by-step please!

Answers
Answer:
Step-by-step explanation:
The smallest perfect square that has three different prime numbers as factor is 900
900 = 30 * 30
Factors = 2² * 3² * 5² = 900
find an equation of the circle that has center (6, -1) and passes through (1, -5)
Answers
an equation of the circle that has center (6, -1) and passes through (1, -5) is 17. one of two numbers and/or letters indicating a point's precise location on a map or graph: Zoom in on the map after entering the GPS coordinates.
What is meant by XY coordinates?The horizontal and vertical addresses of a point in any two-dimensional (2D) space, such as a sheet of paper or a computer display screen, are called the X and Y coordinates, respectively. These coordinates work as a pair to pinpoint a point's precise location.Use the formula (x a) 2 + (y b) 2 = r 2 to determine a circle's equation when you are aware of its radius and center. Here, stands for the circle's center, and is its radius.The equation of a circle has the following formula: (x – h)
2+ (y – k) (y – k)
2 = r2, where (h, k) denotes the circle's center's coordinates and r denotes the circle's radius.
(1-5)
2 +(5—1) (5—1)
2\s=(-4)
2+(-1)
2\s=16+1\s=17
To learn more about XY coordinates refer to:
https://brainly.com/question/28045011
#SPJ1
Answer please i need answer by 11:00 est

Answers
Step-by-step explanation:
2*(1/4)=0.25*2= 0.5 = (2/4)
(2/4) + (3/4)= (5/4) =

(question 15) Find the derivative of the function
using logarithmic differentiation.

Answers
Answer:
\(\textsf{A.} \quad (2+x)^x\left[\dfrac{x}{2+x}+\ln(2+x)\right]\)
Step-by-step explanation:
Replace f(x) with y in the given function:
\(y=(x+2)^x\)
Take natural logs of both sides of the equation:
\(\ln y=\ln (x+2)^x\)
\(\textsf{Apply the log power law to the right side of the equation:} \quad \ln a^n=n \ln a\)
\(\ln y=x\ln (x+2)\)
Differentiate using implicit differentiation.
Place d/dx in front of each term of the equation:
\(\dfrac{\text{d}}{\text{d}x}\ln y=\dfrac{\text{d}}{\text{d}x}x\ln (x+2)\)
First, use the chain rule to differentiate terms in y only.
In practice, this means differentiate with respect to y, and place dy/dx at the end:
\(\dfrac{1}{y}\dfrac{\text{d}y}{\text{d}x}=\dfrac{\text{d}}{\text{d}x}x\ln (x+2)\)
Now use the product rule to differentiate the terms in x (the right side of the equation).
\(\boxed{\begin{minipage}{5.5 cm}\underline{Product Rule for Differentiation}\\\\If $y=uv$ then:\\\\$\dfrac{\text{d}y}{\text{d}x}=u\dfrac{\text{d}v}{\text{d}x}+v\dfrac{\text{d}u}{\text{d}x}$\\\end{minipage}}\)
\(\textsf{Let}\; u=x \implies \dfrac{\text{d}u}{\text{d}x}=1\)
\(\textsf{Let}\; v=\ln(x+2) \implies \dfrac{\text{d}v}{\text{d}x}=\dfrac{1}{x+2}\)
Therefore:
\(\begin{aligned}\dfrac{1}{y}\dfrac{\text{d}y}{\text{d}x}&=x\cdot \dfrac{1}{x+2}+\ln(x+2) \cdot 1\\\\\dfrac{1}{y}\dfrac{\text{d}y}{\text{d}x}&= \dfrac{x}{x+2}+\ln(x+2)\end{aligned}\)
Multiply both sides of the equation by y:
\(\dfrac{\text{d}y}{\text{d}x}&=y\left( \dfrac{x}{x+2}+\ln(x+2)\right)\)
Substitute back in the expression for y:
\(\dfrac{\text{d}y}{\text{d}x}&=(x+2)^x\left( \dfrac{x}{x+2}+\ln(x+2)\right)\)
Therefore, the differentiated function is:
\(f'(x)=(x+2)^x\left[\dfrac{x}{x+2}+\ln(x+2)\right]\)
\(f'(x)=(2+x)^x\left[\dfrac{x}{2+x}+\ln(2+x)\right]\)
K
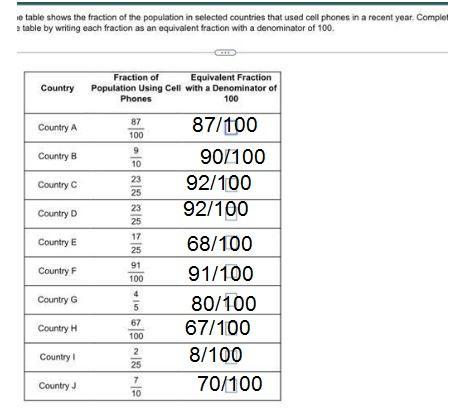
The table shows the fraction of the population in selected countries that used cell phones in a recent year. Complete
the table by writing each fraction as an equivalent fraction with a denominator of 100.
Country
Country A
Country B
Country C
Country D
Country E
Country F
Country G
Country H
Country I
Country J
Fraction of
Equivalent Fraction
Population Using Cell with a Denominator of
Phones
100
87
100
9
10
23
25
23
25
17
25
91
100
4
5
67
100
2
25
...
7
10

Answers
The solution is given below.
What is fraction?A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters.
here, we have,
from the given chart we get,
the solution is attached below.
To learn more on fraction click:
brainly.com/question/10354322
#SPJ1
please the answer fast i need it very importent

Answers
The length of line having mid point B ⇒ 7x - 2.
Given that,
B is the mid point of AC
And also given that
length of segment AB = 2x+5
And length of segment BC = 5x - 7
A straight path established by linking a group of points in a plane is known as a line. It is a one-dimensional form with only a length and no width or height. A line can extend indefinitely in both ends in opposite directions. To indicate a line, we can use upper case characters.
Now since B is the mid point of AC,
So, The line AC is sum of the line segment AB and line segment BC.
Therefore,
AC = AB+BC
= (2x+5)+(5x - 7)
= 7x - 2
Hence,
The length of AC is 7x - 2
Learn more about the equation of line visit:
https://brainly.com/question/18831322
#SPJ1
its Z because it's on -3.5 and 4....its on the graph just look
Answers
Answer:
.,. uhh Where's the question?
Q: give answer in decimal to the nearest tenth of a cm

Answers
Answer:
the nearest tenth of the cm is 6.9 cm
) Assume that a simple random sample has been selected from a normally distributed population and test the given claim at α = 0.05. State the claim mathematically. Identify the null and alternative hypotheses, test statistic, critical region(s), and the decision regarding the null hypothesis. State the conclusion that addresses the original claim. A local group claims that police issue at least 60 speeding tickets a day in their area. To prove their point, they randomly select two weeks. Their research yields the number of tickets issued for each day. The data are listed below. 70 48 41 68 69 55 70 57 60 83 32 60 72 58
Answers
We cannot conclude that there are more than 70,000 defined words in the dictionary.
To test the claim that there are more than 70,000 defined words in the dictionary, we can set up the null and alternative hypotheses as follows:
Null Hypothesis (H0): The mean number of defined words on a page is 48.0 or less.
Alternative Hypothesis (H1): The mean number of defined words on a page is greater than 48.0.
So, sample mean
= (59 + 37 + 56 + 67 + 43 + 49 + 46 + 37 + 41 + 85) / 10
= 510 / 10
= 51.0
and, the sample standard deviation (s)
= √[((59 - 51)² + (37 - 51)² + ... + (85 - 51)²) / (10 - 1)]
≈ 16.23
Next, we calculate the test statistic using the formula:
test statistic = (x - μ) / (s / √n)
In this case, μ = 48.0, s ≈ 16.23, and n = 10.
test statistic = (51.0 - 48.0) / (16.23 / √10) ≈ 1.34
With a significance level of 0.05 and 9 degrees of freedom (n - 1 = 10 - 1 = 9), the critical value is 1.833.
Since the test statistic (1.34) is not greater than the critical value (1.833), we do not have enough evidence to reject the null hypothesis.
Therefore, based on the given data, we cannot conclude that there are more than 70,000 defined words in the dictionary.
Learn more about test statistic here:
https://brainly.com/question/31746962
#SPJ1
How many miles does he run in one year

Answers
Answer Key:
1. Since the question says Mr. Smith runs 2.7 miles every day of the week, you will need to multiply it with 365, the days of the year. The total answer you would get D. 985.5 miles.
| I just want to help you with #2 anyway
A bakery sold 224 chocolate cupcakes in a day, which was 56% of the total number of cupcakes sold that day. How many total cupcakes did the bakery sell that day?
Answers
Hence, 440 cupcakes were sold on that day.
The bakery sold a total of 400 cupcakes that day, with 224 of them being chocolate cupcakes, representing 56 precent of the total.
Use the concept of percentage defined as:
A figure or ratio that may be stated as a fraction of 100 is a percentage. If we need to calculate a percentage of a number, we should divide it by its entirety and then multiply it by 100. The proportion, therefore, refers to a component per hundred.
Given that,
A bakery sold 224 chocolate cupcakes in a day.
The 224 chocolate cupcakes represent 56% of the total number of cupcakes sold that day.
To find the total number of cupcakes sold,
Use the percentage given and some simple math.
If 56% of the cupcakes sold were chocolate cupcakes and that amounts to 224 cupcakes,
Set up the following equation:
0.56 x Total number of cupcakes = 224 cupcakes
To find the total number of cupcakes,
Divide both sides of the equation by 0.56:
Total number of cupcakes = 224 cupcakes / 0.56
Calculating this,
The bakery sold a total of 400 cupcakes that day.
Learn more about the percentage visit:
https://brainly.com/question/24877689
#SPJ3