Which equation represents a line perpendicular to the line shown on the graph?
On a coordinate plane, a line goes through (negative 2, 0) and (0, 4).
y = one-half x minus 2
y = negative one-half x + 3
y = 2 x + 1
y = negative 2 x + 4
Answers
Answer:
A
Step-by-step explanation:
The equation of the perpendicular line is y = -1/2x + 3. The correct option is (B).
What is a Linear equation?A linear equation is a equation that has degree as one.
To find the solution of n unknown quantities n number of equations with n number of variables are required.
The coordinates of the given points are (-2, 0) and (0, 4).
The equation of the line for the given points can be written as follows,
(y - 4)/(x - 0) = (4 - 0)/(0 - (-2))
=> y - 4 = 2x
=> y = 2x + 4
Comparing the above equation with the general equation y = mx + c the slope is given as,
m = 2
Now, the product of the slopes of two perpendicular lines is -1.
Thus, the slope of the perpendicular line is,
m' = -1/2.
In order to find the the correct answer compare all the options with general equation y = mx + c and check if the slope is -1/2 as below,
(a) y = 1/2x - 2
m = 1/2
(b) y = -1/2x + 3
m = -1/2
(c) y = 2x + 1
m = 2
(d) y = -2x + 4
m = -2
Hence, the equation for the line perpendicular to the given line is y = -1/2x + 3.
To know more about linear equation click on,
https://brainly.com/question/11897796
#SPJ2
Related Questions
Find the 66th
term in the following
arithmetic sequence
-92, -85, -78, -71, ...
Answers
Answer:
The \(66\)th term is \(363\).
Step-by-step explanation:
To find the \(n\)th term, the formula is \(7n - 99\). Since we want to find the \(66\)th term, we can plug \(n\) for \(66\). So our expression is now \(7 \cdot 66 - 99 =\) \(66\)th term. Solving this we have
\(462 - 99 = 66\text{th term}\\363 = 66\text{th term}\\\). Therefore, the \(66\)th term is \(\boxed{363}\).
Answer:
a₆₆ = 363
Step-by-step explanation:
the nth term of an arithmetic sequence is
\(a_{n}\) = a₁ + (n - 1)d
where a₁ is the first term and d the common difference
here a₁ = - 92 and d = a₂ - a₁ = - 85 - (- 92) = - 85 + 92 = 7 , then
a₆₆ = - 92 + (65 × 7)
= - 92 + 455
= 363
A car’s odometer measures distance to the nearest 0.1 miles. Which is the most appropriate way to report the distance driven using the car’s odometer?
A. 182 miles
B. 200 miles
C. 181.7 miles
D. 181.77 miles
Answers
Answer:
C. 181.7 miles
Solve 7/2x+7/9x=−17+25/6
Answers
1. Jon waits on tables and is paid $6.75an hour. In a 40-hour period, he earned $310.50 in tips. What were his total earnings?
Answers
Answer:
$617.25
Step-by-step explanation:
$617.25 Because, $310.50(tips) + $306.75(hourly wage)=$617.25
Answer:$580.50
Step-by-step explanation:
:)
What is an equation for the parabola with focus (0, -12) and directrix y = 12
Answers
Given:
Focus of a parabola is (0, -12) and directrix is y = 12.
To find:
The equation of the parabola.
Solution:
General form of a parabola is
\((x-h)^2=4p(y-k)\) ...(i)
where, (h,k) is vertex, (h,k+p) is focus and y=k-p is directrix.
Focus is (0, -12).
\((h,k+p)=(0,-12)\)
\(h=0\)
\(k+p=-12\) ...(ii)
Directrix is y = 12.
\(k-p=12\) ...(iii)
Adding (ii) and (iii), we get
\(2k=0\)
\(k=0\)
Putting k=0 in (ii), we get
\(0+p=-12\)
\(p=-12\)
Putting h=0, k=0 and p=-12 in (i).
\((x-0)^2=4(-12)(y-0)\)
\(x^2=-48y\)
\(-\dfrac{1}{48}x^2=y\)
Therefore, the required equation of parabola is \(y=-\dfrac{1}{48}x^2\).
Brian opens a new savings account, with an interest rate of 3.5% compounded annually. If his
initial deposit is GBP 3000, how many years will it take for his money to grow to GBP 9000?
Answers
If initial deposit is GBP 3000 and the rate is 3.5%,then after 32 years it will reach to GBP 9000.
Given that the initial deposit is GBP 3000 and the rate is 3.5%.
We are required to find the number of years after which the amount will reach to GBP 9000.
Compound interest is basically the addition of interest to the principal sum of a loan or deposit, or in other words, interest on principal plus interest.
Amount after compounding=P\((1+r)^{n}\), where P is principal ,r is rate of interest and n is number of years.
The number of years can be calculated as under:
9000=3000\((1+0.035)^{n}\)
3=\((1.035)^{n}\)
\((1.035)^{32}\)=\((1.035)^{n}\)
By comparing both sides,we will get n=32.
Hence if initial deposit is GBP 3000 and the rate is 3.5%,then after 32 years it will reach to GBP 9000.
Learn more about compound interest at https://brainly.com/question/24924853
#SPJ9
In a math class, the teacher asked the students to find the approximate value of one of the x-coordinates of a point of intersection of two functions: f(x) = 2x2 − 3x + 4 g(x) = 5x − 1 Her students gave her different answers. Which answer is the most accurate?
A.
0.8
B.
0.9
C.
1.9
D.
1.1
Answers
Answer:
A. 0.8Step-by-step explanation:
An easy way is to substitute values into both equations and compare:
A. x = 0.8
f(x) = 2(0.8)² - 3(0.8) + 4 = 2.88g(x) = 5(0.8) - 1 = 3B. x = 0.9
f(x) = 2(0.9)² - 3(0.9) + 4 = 2.92g(x) = 5(0.9) - 1 = 3.5C. x = 1.9
f(x) = 2(1.9)² - 3(1.9) + 4 = 5.52g(x) = 5(1.9) - 1 = 8.5D. x = 1.1
f(x) = 2(1.1)² - 3(1.1) + 4 = 3.12g(x) = 5(1.1) - 1 = 4.5As we see the most accurate one is A
Let's graph both function(Attached)
Let's round 0.775
\(\\ \sf\longmapsto 0.775\)
\(\\ \sf\longmapsto 0.77\)
\(\\ \sf\longmapsto 0.8\)
Option A is correct

When finding the area of a rectangular prism, do you prefer to find the area of the base first and then multiply it by the height or to multiply all three dimensions at once?
Answers
Answer: I prefer to find the area of the base first and then multiply by the height
Graph a line with a slope of 2/5 that contains the point (-2 4)
Answers
Answer:
The equation for the line is y = 2/5x + 24/5
Step-by-step explanation:
If you need the exact points, go to m4thway and plug that equation in.
10. Julio's father is 3 times as old as Julio. The sum of their ages is no less than 50. What is the youngest age Julio can be?A. Write an equality that shows the relationship between Julio’s and his father’s ages.B. Solve the equation using a T-chart. Justify each step with a mathematical propertyGiven InequalityC. What does your solution tell you?


Answers
• Letter A)
If 'y' is the age of Julio's father and 'x' the age of Julio, the equality will be:
\(3x=y\)• Letter B)
To solve the equation we have to consider the second part of the exercise: "The sum of their ages is no less than 50". This means:
\(x+y\ge50\)Now we can put the value of y that we have found in the letter A to find the value of 'x':
\(x+3x\ge50\)\(4x\ge50\)\(x\text{ }\ge\text{ 12.5}\)Then the youngest age that Julio can be is 12.5 years! If x is equal to 12.5, Julio's father will have:
\(3\times12.5\text{ = }37.5\text{ years}\)• Letter C)
The solution tells that if Julio has 12.5 years old, his father will have 37.5 years old!
A
Angle ABC Is a right angle.
The measure of angle
DBC is 55°.
The measure of angle ABD Is x
55°
What is the value of x?
B

Answers
Answer:
25
Step-by-step explanation:
ABC is a right angle so ABD and DBC are complementary angles and their sum is equal to 90:
x + 55 = 90 subtract 55 from both sides
x = 25
If 5 is increased to 9, the increase is what percentage of the original number
Answers
Answer: It's a 80% increase
Step-by-step explanation:
help me I don't get this ?
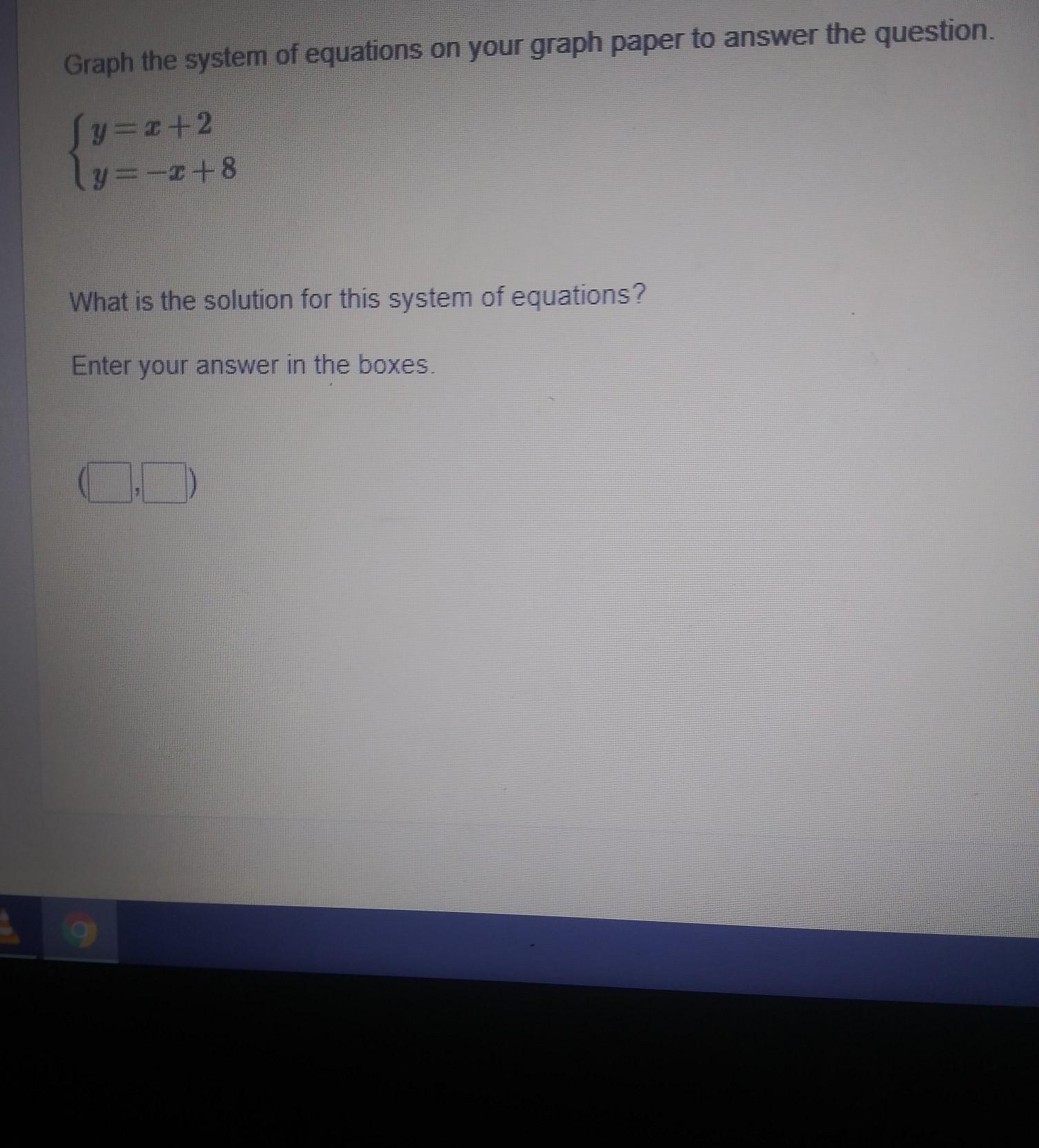
Answers
Answer:
Solution: (3,5)
Step-by-step explanation:
y = x + 2 and
y = - x + 8
y = y
x + 2 = -x + 8
x + x = 8 - 2
2x = 6
x = 6/2
x = 3
Substitute x for 3 in one of the equations to find y.
y = 3 + 2
y = 5
Jayson reads the first 48 pages of a 480-page book in 3 days. Marcus reads the first 50 pages of a 400-page book in 4 days. Nina reads the first 120 pages of a 600-page book in 5 days. If they continue to read at these rates, who will finish first?
Answers
Answer:
Nina will finish first.
Step-by-step explanation:
Let's calculate how many pages each person reads in one day:
Jayson ⇒ 48 pages / 3 days = 16 pages/dayMarcus ⇒ 50 pages / 4 days = 12.5 pages/dayNina ⇒ 120 pages / 5 days = 24 pages/dayThen we divide the number of pages of each book by reading speed of the respective person:
Jayson ⇒ 480 pages ÷ 16 pages/day = 30 days Marcus ⇒ 400 pages ÷ 12.5 pages/day = 32 days Nina ⇒ 600 pages ÷ 24 pages/day = 25 daysThus Nina will take the shortest time finishing her book.
Answer:
Step-by-step explanation:
the amswer is nina
Help solve this thanks

Answers
Answer:
Step-by-step explanation:
7h - 5 = 4
7h = 9
h = 9/7
21(9/7) - 15 = 12
This season, the probability that the Yankees will win a game is 0.56 and the probability that the Yankees will score 5 or more runs in a game is 0.61. The probability that the Yankees lose and score fewer than 5 runs is 0.32. What is the probability that the Yankees will lose when they score fewer than 5 runs? Round your answer to the nearest thousandth.
Answers
The probability that the Yankees will lose when they score fewer than 5 runs is 0.821 (nearest to the thousandth).
What is the chain rule in probability for two events?For two events A and B:
The chain rule states that the probability that A and B both occur is given by:
\(P(A \cap B) = P(A)P(B|A) = P(B)P( A|B)\)
Lets suppose here that:
A = event that Yankees win a gameB = event that Yankees will score ≥ 5 in a gameSuppose A' and B' are their complementary events, then we have:
A' = event that Yankees will lose a gameB' = event that Yankees will score < 5 in gameThen, by the given data, we have:
\(P(A) = 0.56\\P(B) = 0.61\\P(A' \cap B') = 0.32\)
We've to find \(P(A' | B')\)
Using chain rule, we have:
\(P(A'|B') = \dfrac{P(A' \cap B')}{P(B')}\)
Since P(B') = 1-P(B) = 100.61 = 0.39, therefore, we get:
\(P(A'|B') = \dfrac{P(A' \cap B')}{P(B')} = \dfrac{0.32}{0.39} \\\\P(A'|B') \approx 0.821\)
Thus, the probability that the Yankees will lose when they score fewer than 5 runs is 0.821
Learn more about probability here:
brainly.com/question/1210781
Select the exact value of x that can be approximated to x≈0.41 when rounded to the nearest hundredth.

Answers
In order to find the correct option, let's calculate the value of x in each option and round it to the nearest hundredth:
\(\begin{gathered} x=\frac{log94}{5log9} \\ x=\frac{1.9731278}{5*0.9542425} \\ x=\frac{1.9731278}{4.7712125} \\ x=0.41 \\ \\ x=\frac{log65}{12log14} \\ x=\frac{1.8129}{12*1.146128} \\ x=\frac{1.8129}{13.753536} \\ x=0.13 \\ \\ x=\frac{log450}{22} \\ x=\frac{2.6532}{22} \\ x=0.12 \\ \\ x=\frac{3log66}{log7} \\ x=\frac{3*1.81954}{0.8451} \\ x=\frac{5.45862}{0.8451} \\ x=6.46 \end{gathered}\)Therefore the correct option is the first one.
Give another name for line r

Answers
Answer:
line AC
Step-by-step explanation:
because those are two points along line r
it can't be line AB because that would make it a line segment
Answer:
Line ac
Step-by-step explanation:
Which of the following transformations to ∆ABC would NOT preserve size and shape
Answers
Answer:
The answer is below
Step-by-step explanation:
The question is not complete, but I would show how to solve it.
Transformation is the movement of a point from its initial location to a new location. Transforming an object involves transforming all its points. Types of transformation is reflection, rotation, translation and dilation.
Rigid transformations are transformations that preserves the size and shape of an object. There are three types of rigid transformation which are:
Rotation: This involves rotating a shape about a point.Reflection: This is the flipping of a shape across a lineTranslation: This is the sliding of an object up or down.Dilation is the enlargement or reduction of shape of an object. Dilation is not a rigid transformation because it does not preserve the shape or size of the object.
Find the value of n for which the division of x^2n-1 by x+3 leave remainder of -80.
Answers
The value of 'n' for which the division of x^(2n-1) by x + 3 leaves a remainder of -80 is n = 1.
To find the value of 'n' for which the division of x^(2n-1) by x + 3 leaves a remainder of -80, we can use polynomial long division. Let's perform the division step by step:
Write the dividend and divisor in polynomial long division format:
_________________________
x + 3 │ x^(2n-1) + 0x^(2n-2) + 0x^(2n-3) + ...
Divide the leading term of the dividend (x^(2n-1)) by the leading term of the divisor (x). The result is x^(2n-1)/x = x^(2n-2).
Multiply the divisor (x + 3) by the quotient obtained in the previous step (x^(2n-2)). The result is x^(2n-2) * (x + 3) = x^(2n-1) + 3x^(2n-2).
Subtract the result obtained in step 3 from the original dividend:
x^(2n-1) + 0x^(2n-2) + 0x^(2n-3) + ... - (x^(2n-1) + 3x^(2n-2)) = -3x^(2n-2) + 0x^(2n-3) + ...
Bring down the next term of the dividend (which is 0x^(2n-3)) and repeat steps 2-4 until the remainder is constant.
Since we are given that the remainder is -80, we can set the remainder equal to -80 and solve for 'n'.
-3x^(2n-2) + 0x^(2n-3) + ... = -80
Since the remainder is constant (-80), it means that all the terms with x have been canceled out in the division process. Therefore, we can deduce that the highest power of x in the divisor (x + 3) is 0.
This implies that x^(2n-2) = 0, and for any value of 'n', the exponent 2n-2 should be equal to zero. Solving this equation:
2n-2 = 0
2n = 2
n = 1
Therefore, the value of 'n' for which the division of x^(2n-1) by x + 3 leaves a remainder of -80 is n = 1.
for such more question on remainder
https://brainly.com/question/825875
#SPJ8
If m rst= 12x-1, m rsu = 9x-15 and m ust = 53 find each measure

Answers
Answer:
x = 13
m<RST = 155°
m<RSU = 102°
Step-by-step explanation:
m<RST = (12x - 1)°
m<RSU = (9x - 15)°
m<UST = 53°
m<UST + m<RSU = m<RST (angle addition postulate)
53 + (9x - 15) = (12x - 1) (substitution)
Solve for x
53 + 9x - 15 = 12x - 1
53 - 15 + 9x = 12x - 1
38 + 9x = 12x - 1
Subtract 12x from each side
38 + 9x - 12x = 12x - 1 - 12x
38 - 3x = - 1
Subtract 38 from each side
38 - 3x - 38 = -1 - 38
-3x = -39
Divide both sides by -3
x = 13
m<RST = (12x - 1)°
Plug in the value of x
m<RST = 12(13) - 1 = 156 - 1 = 155°
m<RSU = (9x - 15)°
m<RSU = 9(13)x - 15 = 117 - 15 = 102°
The measures of each angle are:
m<RSU = 102°
m<RST = 155°
m<UST = 53°
The given parameters are:
m<RST = (12x - 1)°
m<RSU = (9x - 15)°
m<UST = 53°
Note that:
m<RST = m<RSU + m<UST
Substitute m<RST = 12x - 1, m<RSU = 9x - 15, and m<UST = 53 into the equation above in order to solve for x
m<RST = m<RSU + m<UST
12x - 1 = 9x - 15 + 53
12x - 9x = -15 + 53 + 1
3x = 39
x = 39/3
x = 13
To find the measure of <RST, substitute x = 3 into m<RST = 12x - 1
m<RST = 12(13) - 1
m<RST = 155°
To find the measure of <RSU, substitute x = 3 into m<RSU = 9x - 15
m<RSU = 9(13) - 15
m<RSU = 102°
Learn more on angles here: https://brainly.com/question/14362353
Question 1(Multipl no e Choice Worth 2 points)
(04.04 LC) b
Soybean type 1 yielded 125 bushels per acre last year at a research farm. This year, soybean type 2, planted in the same location, yielded only 100 bushels per acre and there was a
drought. The researchers do not know whether the difference is a result of the superiority of type 1 soybeans or the drought. What is this an example of?
O Bias
O Matched-pairs design
O The placebo effect
O Confounding variable
O Replication
Answers
Answer: Confounding Variable
Step-by-step explanation:
Answer: Confounding variables
Step-by-step explanation:
Took exam and got it correct
Show your work please help me it’s due tomorrow!!!!

Answers
Answer: Consider me the brainiest. The answer is... Decimal form =4.083
Exact form= 49/12
The mixed number form=4 1/12
How do we solve fractions step by step?
Conversion a mixed number 2 1/3 to a improper fraction: 2 1/3 = 2 1/3 = 2 3 + 1/3 = 6 + 1/3 = 7/3
To find a new numerator
A; Multiply the whole number 2 by the denominator 3. Whole number 2 equally 2 * 3/3 = 6/3
b) Add the answer from the previous step 6 to the numerator 1. The new numerator is 6 + 1 = 7
c) Write a previous answer (new numerator 7) over the denominator 3.
Two and one-third are seven-thirds.
Conversion a mixed number 1 3/4 to a improper fraction: 1 3/4 = 1 3/4 = 1 · 4 + 3/4 = 4 + 3/4 = 7/4
To find a new numerator:
a) Multiply the whole number 1 by the denominator 4. Whole number 1 equally 1 * 4/4 = 4/4
b) Add the answer from the previous step 4 to the numerator 3. The new numerator is 4 + 3 = 7
c) Write a previous answer (new numerator 7) over the denominator 4. One and three quarters are seven quarters.
Add: 7/3 + 7/4 = 7 · 4/3 · 4 + 7 · 3/4 · 3 = 28/12 + 21/12 = 28 + 21/12 = 49/12 It
is suitable to adjust both fractions to a common (equal, identical) denominator for adding, subtracting, and comparing fractions. The common denominator you can calculate as the least common multiple of both denominators - LCM(3, 4) = 12. It is enough to find the common denominator (not necessarily the lowest) by multiplying the denominators: 3 × 4 = 12. In the following intermediate step, it cannot further simplify the fraction result by cancelling. In other words - seven thirds plus seven quarters is forty-nine twelfths.
An investment of $8500 increases in value by 4.5% every year. How long until the investment reaches about $17323.
Answers
Answer:
It would take 16 years and 64 days until the investment reaches about $ 17323
Step-by-step explanation:
Given that an investment of $ 8500 increases in value by 4.5% every year, to determine how long it would take until the investment reaches about $ 17323, the following calculation must be performed:
8,500 x (1 + 0.045 / 1) ^ X = 17,323
8,500 x 1,045 ^ X = 17,323
1,045 ^ X = 17,323 / 8,500
1.045 ^ X = 2.038
1,045 ^ 16,175 = 2,038
X = 16.175
1 = 365
0.175 = X
0.175 x 365 = X
63.875 = X
Therefore, it would take 16 years and 64 days until the investment reaches about $ 17323
If f(-5)=7 identify a point on the graph of f
Answers
Answer:
If f(-5) = 7, then the point P(-5, 7) will be on the graph of f
where -5 is the x-coordinate and 7 is the y-coordinate
Step-by-step explanation:
In 2005 an area vocational school had an enrollment of 325 men and 123 women. In 2006 there were 149 women. what was the percent increase of women students. The answer should be rounded to the nearest whole percent
Answers
The nearest Whole percent, the percent increase of women students is approximately 21%.
The percent increase of women students, we need to compare the number of women students in 2005 and 2006.
In 2005, the number of women students was 123.
In 2006, the number of women students was 149.
To find the increase, we subtract the initial value (2005) from the final value (2006):
Increase = Final Value - Initial Value
Increase = 149 - 123
Increase = 26
Next, we need to calculate the percent increase. The percent increase is given by the formula:
Percent Increase = (Increase / Initial Value) * 100
Plugging in the values:
Percent Increase = (26 / 123) * 100
Calculating the percent increase:
Percent Increase ≈ 21.14%
Rounding to the nearest whole percent, the percent increase of women students is approximately 21%.
Therefore, the answer is 21%.
To know more about Whole percent.
https://brainly.com/question/24877689
#SPJ11
Instead of building the enclosure of maximum area, the company wishes to build only a 20,000 square foot enclosure still using up all the fencing and situated with one side on the river. Find the dimensions of the enclosure that will satisfy these requirements by doing the following: 14. What equation can be solved to find the possible widths
Answers
Answer:
x = 80000/L f
Step-by-step explanation:
When using only three sides for fencing a rectangular area, sides will be
"x " and "y " x = 2*y x is the largest side of the rectangular area
we only fence one y side ( the other side is a river
So the perimeter is L = x + 2*y or L = 4*y
On the other hand if now the area will be 20000 f²
A = x*y = 20000 ⇒ y = 20000/ x
As the fence material is the same as that of the maximum area
L = 4*y L = 4* 20000 / x
L*x = 80000
Then x = 80000/L
Where L is the quantity of fencing material
What is the area of the figure? A 80 square inches 88 square inches C. 96 square inches D. 120 square inches
Answers
Answer:
88
Step-by-step explanation:
Daisy cream is sold in a bulk of 76 cups of cream. Kremlin cream is sold in a bulk of 4 1/2 gallons of cream. Marble cream is sold in a bulk of 40 pints of cream. Which one has the most cream?
Answers
Therefore , the solution of the given problem of unitary method comes out to be Daisy cream and Kremlin cream both have less cream per bulk 1 gallon and 4.5 gallons, respectively than Marble cream.
An unitary method is what?The objective can be accomplished by utilising what has already been discovered, taking advantage of this worldwide access, and including all essential components from earlier changeable study who employed a certain technique. If the anticipated claim outcome actually occurs, it will either be possible to contact the variable again or both important processes will undoubtedly miss the statement.
Here,
We must convert cups to gallons because daisy cream is sold in bulks of cups. Since a gallon of Daisy cream comprises 16 cups, one quantity of Daisy cream contains:
=> 16 cups per bulk = 1 gallon 16 cups per bulk = 1 gallon
Moscow cream is offered in bulk quantities of 4 1/2 gallons, which is one gallon.
Thus, we must convert pints to gallons. A gallon of Marble cream comprises eight pints, hence one quantity of Marble cream contains:
=> 40 pints in a bulk equal 1 gallon, 8 pints, or 5 gallons.
As a result, we can see that Marble cream, with 5 gallons per bulk, has the most cream.
Daisy cream and Kremlin cream both have less cream per bulk (1 gallon and 4.5 gallons, respectively) than Marble cream.
To know more about unitary method visit:
https://brainly.com/question/28276953
#SPJ1
Describe at least two advantages to using stemplots rather than frequency distributions
Answers
Answer:
Suppose that a data set has a minimum value of 18 and a max of 83 and that you want 5 classes. Explain how to find the class width for this frequency table. What happens if you mistakenly use a class width of 13 instead of 14?
Step-by-step explanation: