Answers
The answer is \(\frac{a+2}{a-1}\)
\(\frac{\frac{a^{2}+5 a+6}{a^{2}-1}}{\frac{a^{2}-9}{a^{2}-2 a-3}}\)
Apply the fraction rule: \($\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{a \cdot d}{b \cdot c}$\)
\($\frac{\left(a^2+5 a+6\right)\left(a^2-2 a-3\right)}{\left(a^2-1\right)\left(a^2-9\right)}$\)
Factor \($a^2+5 a+6: \quad(a+2)(a+3)$\)
\($=\frac{(a+2)(a+3)\left(a^2-2 a-3\right)}{\left(a^2-1\right)\left(a^2-9\right)}$\)
Factor \($a^2-9: \quad(a+3)(a-3)$\)
\($=\frac{(a+2)(a+3)\left(a^2-2 a-3\right)}{\left(a^2-1\right)(a+3)(a-3)}$\)
Cancel the common factor: \($a+3$\)
\(=\frac{(a+2)\left(a^2-2 a-3\right)}{\left(a^2-1\right)(a-3)}\)
Factor \($a^2-2 a-3: \quad(a+1)(a-3)$\)
\(=\frac{(a+2)(a+1)(a-3)}{\left(a^2-1\right)(a-3)}\)
Cancel the common factor: \(a-3$ $=\frac{(a+2)(a+1)}{a^2-1}$\)
Factor \(a^2-1: \quad(a+1)(a-1)$ $=\frac{(a+2)(a+1)}{(a+1)(a-1)}$\)
Cancel the common factor: \(a+1$ $=\frac{a+2}{a-1}$\)
The mathematical method for expressing a portion of a whole is through fractions. They take the shape of a denominator and a numerator. The bottom component (which shows how many equal parts we have divided into a whole) is known as the denominator, and the higher part (or the part that reflects how much of anything entire we are examining) is known as the numerator.
To divide fractions, we must memorize a number of rules and take a number of actions. The reciprocal of the second fraction must be multiplied by the first fraction. Division requires the following actions to be taken: Substitute the multiplicand (×) for the division sign (÷). The reciprocal of the second term or fraction must be written if the sign of division is changed from division to multiplication. To reach the needed result, we just multiply them at the end.
Learn more about fraction rule https://brainly.com/question/18315507
#SPJ9
Related Questions
El costo de producir 10 juegos de video al día es de 350 dólares , mientras que producir 30 juegos del mismo tipo al día cuestan 850 dólares . Si suponemos un modelo lineal como el descrito anteriormente , determine
Answers
Answer:
El coste de producir un juego de vídeo es de 125 dólares.
Step-by-step explanation:
(This exercise is written in Spanish and is incomplete. Complete statement will be presented below)
El costo de producir 10 juegos de video al día es de 350 dólares , mientras que producir 30 juegos del mismo tipo al día cuestan 850 dólares . Si suponemos un modelo lineal como el descrito anteriormente , determine:
¿Cuál es el costo de producir un juego de vídeo?
(Explanation will be held in Spanish)
El modelo lineal es un polinomio de primer orden de la forma:
\(y = a\cdot x + b\)
Donde:
\(x\) - Variable independiente (eje x - Cantidad de juegos de vídeo producidos - Adimensional)
\(y\) - Variable dependiente (eje y - Coste de producción de juegos de vídeo - Dólares)
\(a\) - Pendiente de la función.
\(b\) - Intercepto en el eje y.
Dados los dos costes para dos cuotas distintas de producción, se construye el siguiente sistema de ecuaciones lineales:
\(10\cdot a + b = 350\)
\(30 \cdot a + b = 850\)
Se resuelve el sistema con algo de manipulación algebraica:
\((30\cdot a + b) - (10\cdot a + b) = 850 - 350\)
\(20 \cdot a = 500\)
\(a = 25\)
Luego:
\(b = 850 - 30\cdot a\)
\(b = 100\)
La ecuación lineal es:
\(y = 25\cdot x +100\)
Finalmente, el coste de producir un juego de vídeo es:
\(y = 25 \cdot (1) + 100\)
\(y = 125\)
El coste de producir un juego de vídeo es de 125 dólares.
Determine if the function f is an exponential function. If so, identify the base. If not, why not? f(x) = x^e
Answers
Answer:
It is not exponential because it is f(x)= x-3.141.
Step-by-step explanation:It is a slope-intercept formula. An exponential formula is y=a^x
Mr.Jones bought a box of 144 chocolate bars for $72.00 for his convenience store. He marks the price up by 50% . What is the price of one chocolate bar?
Answers
Answer:
A box of 144 chocolate bars for 72 dollar.
Then each chocolate bar costs: 144/72 = 2 dollar
=> Price up to 50%: P = 2 x (1 + 50/100) = 2 x 3/2 = 3 dollar
Hope this helps!
:)
I'm confused on it i need a explanation

Answers
Answer:
x = 19°
Step-by-step explanation:
are adjacent angles, so the sum is 180°
so
8x-7+x+16=180°
9x = 180 + 7 - 16
9x = 171
x = 171 : 9
x = 19
---------------------------
check
8 * 19 - 7 + 19 + 16 = 180 (remember PEMDAS)
180 = 180
the answer is good
5. Domingo earns $13 dollars per hour and worked 47.5 hours that week. He is paid
double time for all hours worked over 40 hours in one week. What is his gross pay
for the week?
Answers
Answer:
$715
Step-by-step explanation:
$13 x 40 hours = $520
47.5 hours - 40 hours = 7.5 overtime hours
2 x $13 = $26 per overtime hour
$26 x 7.5 = $195
$520 + $195 = $715
What are the x-intercept and the y-intercept of the graph of 9x − 7y = −63?A.x-intercept: 7; y-intercept: −9B.x-intercept: −7; y-intercept: 9C.x-intercept: 9; y-intercept: −7D.x-intercept: −9; y-intercept: 7
Answers
Equation of a line:
9x - 7y = -63
To find the x-intercept we have to substitute y = 0 into the equation, as follows:
9x - 7*0 = -63
9x = -63
Dividing by 9 at both sides of the equation:
9x/9 = -63/9
x = -7
To find the y-intercept we have to substitute x = 0 into the equation, as follows:
9*0 - 7y = -63
-7y = -63
Dividing by -7 at both sides of the equation:
-7y/(-7) = -63/(-7)
y = 9
Answer
x-intercept: −7; y-intercept: 9
A number which was tripled and added to 4, totals 40. What is the number?
Answers
Answer:
x=12
Step-by-step explanation:
Our equation: 3x + 4= 40
40-4=36. 36/3 = 12
the following table shows the number of miles a hiker walked on a trail each day for 6 days. day 1 2 3 4 5 6 number of miles 8 5 7 2 9 8 what was the mean number of miles the hiker walked for the 6 days? responses 3.5 3.5 4.5 4.5 6.5 6.5 7.5 7.5 8
Answers
The mean number of miles the hiker walked for the 6 days was 6.5 miles.
To calculate the mean or average of a set of numbers, we add up all the numbers and then divide the sum by the number of items in the set. In this case, we have the number of miles the hiker walked on each of the six days. To find the total number of miles the hiker walked, we simply add up all the numbers
8 + 5 + 7 + 2 + 9 + 8 = 39
Next, we divide the total number of miles by the number of days (which is 6) to get the average or mean number of miles the hiker walked per day:
Mean number of miles = Total number of miles / Number of days
= 39 / 6
= 6.5
Learn more about mean here
brainly.com/question/22871228
#SPJ4
Find the velocity of the car at the end of a drag race. Round to the nearest whole number.

Answers
Answer:
183 miles per hour.
Explanation:
The estimated velocity(v) at the end of a drag race is modeled using the formula below:
\(v=234\sqrt[3]{\frac{p}{w}}\)Given:
• The horsepower, p = 1311
,• The weight (in pounds), w = 2744 pounds.
Substitute into the formula above:
\(\begin{gathered} v=234\sqrt[3]{\frac{1311}{2744}}=182.9 \\ v\approx183\text{ miles per hour} \end{gathered}\)The velocity is approximately 183 miles per hour.
Multiply the following radicals (do NOT simplify)
2/4 x 4/6
Answers
Answer:
0.33333333333
Step-by-step explanation:
You divide 2÷4×4÷6= 0.33333333333
Answer:
8/24
Step-by-step explanation:
2/4 x 4/6
All you need to do is multiply from across
2*4 = 8 (numerator)
6 * 4 = 24 (denominator)
8/24
PLEASE HELP WILL GIVE BRAINLIEST
An object is launched into the air. The projectile motion of the object can be modeled using the function
h(t) = –16t2 + 72t + 5, where t is the time in seconds since the launch and h(t) represents the height in feet of the object after t seconds. What is true about the projectile motion of this object? Check all that apply.
The initial height is 5 feet.
The initial velocity of the object is –72 feet/second.
The object will hit the ground after approximately 4.57 seconds.
After 3 seconds, the object is 173 feet high.
At t = 0, h(t) = 0.
Answers
Answer:
The initial height is 5 feet.
The initial velocity of the object is –72 feet/second.
The object will hit the ground after approximately 4.57 seconds.
After 3 seconds, the object is 173 feet high.
So t = 0, h(t) = 0
Step-by-step explanation:
Write the equation g(x) of the transformation of the parent graph f(x) = |x| reflected over the x axis.
Answers
Answer:
g(x) = -|x|
Step-by-step explanation:
f(x) = |x|
y = −f(x) Reflects it about x-axis
g(x) = -|x|
We start off with: f(x) = |x|
Reflection across x-axis
y = -f(x)
After: g(x) = -|x|
Best of Luck!
4x(x + y) - y (x + y)
=
Answers
Answer:
=4x2+3xy−y2
Hope this helps you
Simplify |(1/4-1/5)+(-3/4+1/8)|
Answers
The simplified expression of |(1/4-1/5)+(-3/4+1/8)| is |-0.57|.
What is LCM?In mathematics, the value that is equally divided by the two supplied numbers is known as the LCM of any two. Least Common Multiple is its full name. Another name for it is the Least Common Divisor (LCD). As an illustration, LCM (4, 5) = 20. In this case, the LCM 20 may be divided by both 4 and 5, hence these two numbers are referred to as the divisors of 20.
When the fractions' denominators differ, LCM can also be used to add or subtract any two fractions. LCM is used to make the denominators common when doing any arithmetic operations using fractions, such as addition and subtraction.
The given expression is:
|(1/4-1/5)+(-3/4+1/8)|
Take the LCM:
|(5 - 4)/ 20 + (-24 + 4) 32|
|1/20 - 20/32|
Take the LCM:
|(32 - 400) / 640|
|-368 / 640|
|-0.57|
Hence, the simplified expression of |(1/4-1/5)+(-3/4+1/8)| is |-0.57|.
Learn more about LCM here:
https://brainly.com/question/24510622
#SPJ1
Hailey invested $95,000 in an account paying an interest rate of 7\tfrac{1}{4}7 4 1 % compounded continuously. Brooklyn invested $95,000 in an account paying an interest rate of 6\tfrac{5}{8}6 8 5 % compounded monthly. After 10 years, how much more money would Hailey have in her account than Brooklyn, to the nearest dollar?
Answers
Answer:12220
Step-by-step explanation:
2t−5=−10
Helpppppp
Plz
Answers
Answer:
t= -2.5
Step-by-step explanation:
2t−5=−10
add 5 to both sides
2t= -5
divide by 2
t= -2.5
A parachutist's rate during a free fall reaches 207 kilometers per hour. What is this rate in meters per second? At this rate, how many meters will the parachutist fall during 10 seconds of a free fall?
Answers
To convert kilometers per hour to meters per second, we need to divide by 3.6. Therefore, the parachutist's rate during free fall in meters per second is:
207 km/h ÷ 3.6 = 57.5 m/s
To find the distance the parachutist will fall during 10 seconds of free fall, we can use the formula:
distance = 1/2 x acceleration x time^2
The acceleration due to gravity is approximately 9.8 m/s^2. Therefore, the distance the parachutist will fall during 10 seconds of free fall is:
distance = 1/2 x 9.8 m/s^2 x (10 s)^2 = 490 m
So the parachutist will fall 490 meters during 10 seconds of free fall at a rate of 207 kilometers per hour, which is equivalent to 57.5 meters per second.
To know more about speed,distance and time, visit:
https://brainly.com/question/18212279
#SPJ11
Consider the function z = f(x,y) = 6x^2 - 2x + 2y^2-3y+7xy+3
a. Compute the partial derivatives
dz/dx:
dz/dy:
b. Find the critical point of f
(x,y) =
c. starting at (x,y) = (3,4); a small increase in y with x held constant will lead to a ___ increase in z than a small increase in x with y held constant
d. suppose a and b are fixed positive numbers and that a is greater than b. Which of the following is larger?
the slope of f(a,y) at y =3
the slope of f(b,y) at y = 3
Answers
dz/dx = 12x + 7y - 2; dz/dy = 4y + 7x - 3
The critical point of f(x,y) is (1/6,3/4).
A small increase in y with x held constant will lead to a larger increase in z than a small increase in x with y held constant.
The slope of f(a,y) at y = 3 is larger.
a) To find the partial derivative dz/dx, differentiate the function with respect to x, treating y as a constant:
dz/dx = 12x + 7y - 2.
To find the partial derivative dz/dy, differentiate the function with respect to y, treating x as a constant:
dz/dy = 4y + 7x - 3.
b) To find the critical point of f(x,y), set both partial derivatives equal to zero and solve for x and y: 12x + 7y - 2 = 0 and 4y + 7x - 3 = 0. Solving these equations simultaneously, we get x = 1/6 and y = 3/4, which is the critical point.
c) To determine the effect of small increases in x and y on z, we can compare the partial derivatives. Since dz/dy is larger than dz/dx at (3,4), a small increase in y with x held constant will lead to a larger increase in z than a small increase in x with y held constant.
d) To compare the slopes of f(a,y) and f(b,y) at y = 3, we need to compute dz/dy at y = 3 for both functions. Substituting y = 3 into the expression for dz/dy from part (a), we get dz/dy = 25a - 5 for f(a,y) and dz/dy = 25b - 5 for f(b,y). Since a is greater than b, it follows that the slope of f(a,y) at y = 3 is larger.
For more questions like Slope click the link below:
https://brainly.com/question/3605446
#SPJ11
please help me. this is a geometry problem

Answers
Step-by-step explanation:
"bisects" means "cuts in half".
that is the whole "secret" for that problem.
now we know, that both line segments are equally long (exactly half of the total length of UV).
so,
4x - 9 = 2x + 5
2x = 14
x = 7
This is just a question to answer to boost your points. (students who need points to find answers only!)
What is the correct answer to 5x5/2?
Answers
Answer:
it would be 12.5
Step-by-step explanation:
brainly deleted my answer from before
May someone please help me.

Answers
Answer: x=9
Step-by-step explanation:
Here the given angles are,
50,80,6x-4
The sum of the angles of a triangle is 180 degrees and hence
50+80+6x-4=180
130+6x-4=180
126+6x=180
6x=180-126
6x=54
x=54/6
x=9
For further explanation about the question,
https://brainly.com/question/18533481
Short answer needed ASAP.
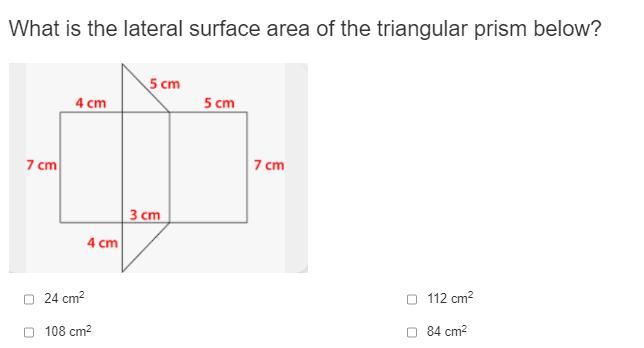
Answers
The triangular prism has a lateral area of 84 square inches. (Correct choice: D)
How to determine the lateral area of a triangular prism
In this problem we find the case of right prism with two right triangular bases, then the lateral area is the sum of the area of three rectangles. The area formula for a rectangle is:
A = w · l
Where:
w - Width, in centimeters.l - Length, in centimeters.Finally, we determine the lateral area of the triangular prism is:
A = (4 cm) · (7 cm) + (3 cm) · (7 cm) + (5 cm) · (7 cm)
A = 28 cm² + 21 cm² + 35 cm²
A = 84 cm²
The lateral area of the triangular prism is equal to 84 square centimeters.
To learn more on lateral areas of prisms: https://brainly.com/question/29007884
#SPJ1
what is one characteristic of a cosine function
Answers
Answer:
c. Its graph is symmetric about the y-axis.
Step-by-step explanation:
need help please this is plato recovery

Answers
\(3\leqslant |x+2|\leqslant 6\implies \begin{cases} 3\leqslant |x+2|\\\\ |x+2|\leqslant 6 \end{cases}\implies \begin{cases} 3 \leqslant \pm (x+2)\\\\ \pm(x+2)\leqslant 6 \end{cases} \\\\[-0.35em] ~\dotfill\)
\(3\leqslant +(x+2)\implies \boxed{3\leqslant x+2}\implies 1\leqslant x \\\\[-0.35em] ~\dotfill\\\\ 3\leqslant -(x+2)\implies \boxed{-3\geqslant x+2}\implies -5\geqslant x \\\\[-0.35em] ~\dotfill\\\\ +(x+2)\leqslant 6\implies \boxed{x+2\leqslant 6}\implies x\leqslant 4 \\\\[-0.35em] ~\dotfill\\\\ -(x+2)\leqslant 6\implies \boxed{x+2\geqslant -6}\implies x\geqslant -8\)
The Wright family purchased a portable movie screen for their backyard. It is held up with poles and guy wires on each side of the screen, as shown in the diagram.
a. If AE = 6 feet, what is the angle of elevation of the guy wire AD? Round to the nearest degree.
b. What is the length of the guy wire? Round to the nearest tenth
c. How much wire is needed for the two guy wires?
d. How long is AB?

Answers
Considering the diagram,
the angle of elevation of the guy wire AD 56.31 degrees
the length of the guy wire 10.8 ft
for the two guy wires 21.6 ft
length AB = 24 ft
How to find the the angle of elevation of the guy wire ADThe angle of elevation is worked using SOH CAH TOA
Sin = opposite / hypotenuse - SOH
Cos = adjacent / hypotenuse - CAH
Tan = opposite / adjacent - TOA
Using tan, TOA
let the angle be x
tan x = Opposite / Adjacent
tan x = 9 / 6
x = arc tan 3/2
x = 56.31 degrees
The length of the guy wire
length of guy wire = √(9^2 + 6^2) = 3√13 = 10.8 ft
for the two guy wires = 10.8 * 2 = 21.6 ft
length AB
= 6 + 12 + 6
= 24 ft
Learn more about SOH CAH TOA here:
https://brainly.com/question/29402966
https://brainly.com/question/29334128
#SPJ1
Explain why the set of natural numbers {1,2,3,4,...} and the set of even numbers {2, 4, 6, 8, . . .} of positive even numbers
Answers
The set of natural numbers {1,2,3,4,...} and the set of positive even numbers {2, 4, 6, 8, . . .} are different because natural numbers include all positive integers, while even numbers only include those that are divisible by 2 with no remainder.
About the setsTwo important sets of numbers are natural numbers and even numbers. The set of natural numbers consists of numbers that are not negative, beginning with 1 and continuing indefinitely with 2, 3, 4, and so on.
The set of even numbers, on the other hand, consists of numbers that are divisible by 2, beginning with 2, 4, 6, and so on.
Positive integers refer to natural numbers. Any integer greater than zero is a positive integer.
Zero is not a positive integer. Hence, the set of natural numbers consists of {1,2,3,4,…}
On the other hand, the set of even numbers consists of {2, 4, 6, 8, . . .}.
Therefore, {1,2,3,4,…} and {2, 4, 6, 8, . . .} are two different sets of numbers where one set is composed of positive integers (natural numbers) and the other is composed of positive even numbers.
Learn more about set in math at
https://brainly.com/question/30339736
#SPJ11
Square RSTU is inside trapezoid RSVU. What is the measure, in degrees, of angle VSR? R. REN T Only 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, -, -, and / are allowed in your answer. Answers that are mixed numbers must be entered as an improper fraction or decimal. Your answer

Answers
Answer:
135°
Step-by-step explanation:
m<VSR = m<RST + m<VST
Each angle at the vertices of a square is equal to 90°. <RST is one of the vertices of square RSTU, therefore,
m<RST = 90°
also, m<VST = 90 - 45 = 45°
m<VSR = m<RST + m<VST
Thus:
m<VSR = \( 90 + 45 = 135 \)
Measure of angle VSR is 135°
The angle VSR will be equal to 135°.
What is an angle?
The angle is defined as the span between two intersecting lines or surfaces at or close to the point where they meet.
m∠VSR = m∠RST + m∠VST
Each angle at the vertices of a square is equal to 90°. ∠RST is one of the vertices of square RSTU, therefore,
m∠RST = 90°
also, m∠VST = 90 - 45 = 45°
m∠VSR = m∠RST + m∠VST
Thus:
m∠VSR = 135
Therefore the measure of angle VSR is 135°
To know more about an angle follow
https://brainly.com/question/25770607
#SPJ5
the distribution of iq (intelligence quotient) is approximately normal in shape with a mean of 100 and a standard deviation of 15.according to the standard deviation rule, % of people have an iq between 55 and 145. do not round.
Answers
According to the standard deviation rule, 99.7% of people have an IQ between 55 and 145.
How to use the Empirical Rule in statistics?The standard deviation rule which is the empirical rule in statistics tells us that for distributions that have the normal shape, approximately 99.7% of the observations will fall within 3 standard deviations of the mean.
Now, In this question the mean is 100, and the standard deviation is 15. Thus, we can say that approximately 99.7% of the observations (IQ scores) fall between 100 − (3 * 15) and 100 + (3 * 15) or between 55 and 145.
Now, approximately 100% − 99.7% = 0.3% of the observations fall outside this interval. Since the normal shape is symmetric, approximately 0.15% of the observations fall above 145.
Read more about Empirical Rule in Statistics at; https://brainly.com/question/10093236
#SPJ4
Solve the following equations. Will give brainliest.

Answers
Answer:
\(x=10^{\frac{4}{3}}=\sqrt[3]{10000}\)
Step-by-step explanation:
Given equation:
\(9^{\log_3 (\log x)}= \log x-2\log^2x+4\)
Rewrite 9 as 3²:
\(\implies (3^2)^{\log_3 (\log x)}= \log x-2\log^2x+4\)
\(\textsf{Apply exponent rule} \quad (a^b)^c=a^{bc}:\)
\(\implies 3^{2\log_3 (\log x)}= \log x-2\log^2x+4\)
\(\textsf{Apply the log power law}: \quad \log_ax^n=n\log_ax\)
\(\implies 3^{\log_3 (\log x)^2}= \log x-2\log^2x+4\)
\(\textsf{Apply log law}: \quad a^{\log_ab}=b\)
\(\implies (\log x)^2= \log x-2\log^2x+4\)
Simplify:
\(\implies\log ^2 x= \log x-2\log^2x+4\)
\(\implies 3\log ^2 x- \log x-4=0\)
Let log(x) = u:
\(\implies 3u^2-u-4=0\)
Factor:
\(\implies 3u^2+3u-4u-4=0\)
\(\implies 3u(u+1)-4(u+1)=0\)
\(\implies (3u-4)(u+1)=0\)
Apply the zero-product property:
\(\implies 3u-4=0 \implies u=\dfrac{4}{3}\)
\(\implies u+1=0 \implies u=-1\)
Substitute u=log(x) back in:
\(\implies \log x = -1\)
\(\implies \log x= \dfrac{4}{3}\)
On the left side of the original equation, we have log₃ (log x).
As logs of negative numbers cannot be taken, log(x)=-1 is not a valid solution since this would give log₃(-1) which is undefined.
Therefore, the only valid solution is:
\(\implies \log x= \dfrac{4}{3}\)
\(\implies x=10^{\frac{4}{3}}\)
\(\implies x=\left(10^4\right)^{\frac{1}{3}}\)
\(\implies x=10000^{\frac{1}{3}}\)
\(\implies x=\sqrt[3]{10000}\)
Note: If a log has no base, assume that the base is 10.
Jaleel made three times as many baskets as John during basketball practice
Answers
Answer:
3x
Step-by-step explanation:
The answer would be 3 times however much john has. So basically like a multiplication question.
