Answers
Answer:
32
Step-by-step explanation:
Related Questions
For the following relation to be considered a function, x cannot be
(12, 13), (-11, 22), (33, 101), (x, 56)
Answers
Answer:
The given relation is not a function if there exist multiple values of y for a single value of x.
We cannot determine whether the relation is a function or not by looking at the first three pairs.
For the fourth pair, we need to ensure that there is only one value of y for any given value of x. Therefore, x cannot be equal to 12, -11, or 33 because those values have already been assigned a specific y value. If x is equal to any of those values, it would create a situation where there are multiple y values for the same x value, violating the definition of a function.
Therefore, x cannot be equal to 12, -11, or 33.
Please help is a choose al that apply

Answers
Answer:
Your answers are:
A, B and C
Step-by-step explanation:
So 12 over 3 is equal to 4 which is a Whole number. meaning Not a fraction, an Integer is a whole number (not a fractional number) that can be positive, negative, or zero. Rational numbers would include this example as well
Hope this helped have a wonderful day/night/afternoon
6. How can you use an equation to make a prediction from a pattern? (1 point)
Answers
Answer: because it has the same numbers
Step-by-step explanation:
prove that ∑ n=2
[infinity]
xln x
n
1
is contimuons on (1,[infinity]) (2) 15∑ n=2
[infinity]
xln x
n
1
uniformly convergent on (1,[infinity]) ? why?
Answers
To prove that the series ∑_(n=2)^(∞) (x ln x)^(n-1) is continuous on the interval (1, ∞), we need to show that the series converges for all x in (1, ∞), and the limit of the series as x approaches any value in (1, ∞) exists.
Let's analyze the convergence of the series. We have:
∑_(n=2)^(∞) (x ln x)^(n-1)
This is a geometric series with the common ratio r = x ln x. In order for the series to converge, the absolute value of the common ratio should be less than 1:
|r| = |x ln x| < 1
Now, let's consider the interval (1, ∞). For any x in this interval, we have:
1 < x
Taking the natural logarithm of both sides, we get:
ln 1 < ln x
0 < ln x
Multiplying by x, we have:
0 < x ln x
Therefore, for all x in (1, ∞), we have 0 < x ln x < 1, which implies that |x ln x| < 1. Hence, the common ratio of the series is less than 1, and the series ∑_(n=2)^(∞) (x ln x)^(n-1) converges for all x in (1, ∞).
Now, let's analyze the uniform convergence of the series on (1, ∞). For uniform convergence, we need to show that the series converges uniformly on the interval (1, ∞), meaning that the series converges to the same limit for all x in (1, ∞).
To determine if the series converges uniformly, we can use the Weierstrass M-test. We need to find a sequence of positive constants M_n such that |(x ln x)^(n-1)| ≤ M_n for all x in (1, ∞) and n ≥ 2, and the series ∑ M_n converges.
Consider the function f(x) = x ln x for x in (1, ∞). Taking the derivative, we have:
f'(x) = 1 + ln x
Since ln x is positive for x in (1, ∞), f'(x) is always positive. This implies that f(x) is an increasing function on (1, ∞).
Let's choose M_n = f(2)^(n-1), where f(2) = 2 ln 2. Now, for all x in (1, ∞) and n ≥ 2, we have:
|(x ln x)^(n-1)| = |f(x)^(n-1)| ≤ |f(2)^(n-1)| = M_n
The series ∑ M_n = ∑ (2 ln 2)^(n-1) is a geometric series with the common ratio r = 2 ln 2, which converges since |r| = |2 ln 2| < 1.
By the Weierstrass M-test, since |(x ln x)^(n-1)| ≤ M_n and ∑ M_n converges, the series ∑_(n=2)^(∞) (x ln x)^(n-1) converges uniformly on the interval (1, ∞).
To summarize:
The series ∑_(n=2)^(∞) (x ln x)^(n-1) is continuous on the interval (1, ∞) because it converges for all x in (1, ∞).
The series ∑_(n=2)^(∞) (x ln x)^(n-1) is uniformly convergent on the interval (1, ∞) because it converges uniformly, as shown by the Weierstrass M-test.
Therefore, the series ∑_(n=2)^(∞) (x ln x)^(n-1) is both continuous and uniformly convergent on the interval (1, ∞).
Learn more about convergent here:
brainly.com/question/31701016
#SPJ11
Which two sets of angles are corresponding angles?
∠a and ∠d; ∠b and ∠c
∠a and ∠e; ∠b and ∠d
∠a and ∠c; ∠b and ∠d
∠a and ∠e; ∠b and ∠c

Answers
Answer:
∠a and ∠d; ∠b and ∠c
Step-by-step explanation:
The two triangles as similar triangles and the scale factor is 2 : 1
The sides measuring 6 and 3 are corresponding sides
The sides measeuring 8 and 4 are ocrreposnding sides
⇒ ∠a and ∠d are corresponding angles
The sides measuring 8 and 4 are corresponding sides
The sides measeuring 4 and 2 are ocrreposnding sides
⇒ ∠b and ∠c are corresponding angles
Use a definite integral to find the area under the curve between the given \( x \)-values. \[ f(x)=\frac{3}{x} \text { from } x=1 \text { to } x=9 \] square units"
Answers
The area under the curve f(x)=3/x from x=1 to x=9 is 3 ln 9 square units.
The definite integral is a mathematical tool used to evaluate the area under a curve. Definite integrals are used to calculate the area between two points on a graph, which is a measure of the total amount of change between the two points.
A definite integral has a lower limit (a) and an upper limit (b). The formula for the definite integral of a function f(x) over the interval [a, b] is given as:∫[a,b] f(x) dx= [F(b) - F(a)]
Where F(x) is the antiderivative of the function f(x).
We can use this formula to find the area under the curve of the given function f(x)=3/x between x=1 and x=9. ∫[1,9] 3/x dx = [3 ln|x|] [1,9] = 3 [ln|9| - ln|1|] = 3 ln|9|
The area under the curve between x=1 and x=9 is approximately 8.69 square units, and it is equal to 3 ln(9).
Hence, the area under the curve f(x)=3/x from x=1 to x=9 is 3 ln 9 square units.
Learn more about Definite integral from the given link!
https://brainly.com/question/27746495
#SPJ11
Please Help 50 POINTS!!

Answers
Answer:
D. \(\frac{(x-7)^2}{8^2} -\frac{(y-2)^2}{7^2}\)
Step-by-step explanation:
hope this helps
Answer: D has the largest perimeter
Step-by-step explanation:
The top numbers of fractions describe the vertex and the bottom number square rooted tells you how long each or wide each part of the asymptote rectangle is.
A.
P = 2(11) + 2(3)
P = 22+6
P=28
B.
P = 2(4) + 2(9)
p = 8 +18
P = 26
C.
P = 2(5) + 2(9)
P = 10 +18
P = 28
D.
P = 2(8) + 2(7)
P = 16 +14
P = 30
A new car is purchased for \$41,000$41,000 and over time its value depreciates by one half every 4 years. What is the value of the car 6 years after it was purchased, to the nearest hundred dollars?
Answers
Calculate the average rate of change from the information provided. Flex Baumgartner set the world record for skydiving when he jumped from approximately 24 miles above the Earth on October 14th, 2012. On one of his text jumps on March 15th, 2012, he jumped from a height of 13.56 miles. It took him approximately 8.13 minutes to land safely. a−0.60 miles per minute b−2.95 miles per minute c−1.67 miles per minute d−1.28 miles per minute
Answers
Answer:
Calculus Applied Calculus In Exercises 1–18, calculate the average rate of change of the given function over the given interval. Where appropriate, specify the units of measurement. [ HINT: See Example 1.] Interval: [ 0.1 , 0.2 ] t ( hours ) 0 1.0 0.2 D ( t ) ( miles ) 0 3 6
Step-by-step explanation:
Please helpp, thank youuu.

Answers
Answer:
16ft
Step-by-step explanation:
use pythagreom thereom
12^2+b^2=20^2 solve
144+b^2=400
b^2= 256 square it
b= 16
Answer:
b=16
Step-by-step explanation:
Solve each system by elimination. 2 x+4 y = 10 3 x+5y = 14.
Answers
The solution to the given system of equations is x = 3 and y = 1.
To solve the system of equations by elimination, we'll eliminate one variable by multiplying one or both of the equations by appropriate constants so that the coefficients of one variable will cancel each other out when we add or subtract the equations.
Let's solve the given system:
1. Multiply the first equation by 3 and the second equation by 2 to make the coefficients of 'x' equal:
Equation 1: 2x + 4y = 10
Equation 2: 3x + 5y = 14
Multiply Equation 1 by 3: 3(2x + 4y) = 3(10) becomes 6x + 12y = 30
Multiply Equation 2 by 2: 2(3x + 5y) = 2(14) becomes 6x + 10y = 28
2. Now, subtract the equation (6x + 10y = 28) from (6x + 12y = 30) to eliminate 'x':
(6x + 12y) - (6x + 10y) = 30 - 28
6x - 6x + 12y - 10y = 2
2y = 2
y = 1
3. Substitute the value of 'y' (which we found to be 1) back into either of the original equations. Let's use the first equation:
2x + 4y = 10
2x + 4(1) = 10
2x + 4 = 10
2x = 10 - 4
2x = 6
x = 6/2
x = 3
Therefore, the solution to the given system of equations is x = 3 and y =1.
Learn more about Variables here:
https://brainly.com/question/15078630
#SPJ11
What is the lateral surface area of the triangular prism shown below?
Responses
40 cm2
150 cm 2
170 cm2
170 cm 2,
190 cm

Answers
The lateral surface area of the triangular prism shown below is C.170 cm².
How can the lateral surface area of the triangular prismbe calculated?The concept that will be used here is triangular prism breakdown and calculation.
We can break down the triangular prism so as to make it simpler as :
We have (2 triangles) as well as ( 2 side rectangles) and (1 back rectangle)
We can calculate the area of triangle as ( ¹/₂ * base * height)
= (¹/₂ * 5 * 4)
=10cm
We can calculate the area of rectangle as ( length * width)
=(10 * 5)
=50
Then the Area of trapezoid = 2(10) + 3(50)
=20 + 150
= 170 cm²
Therefore, option C is correct.
Learn more about triangular prism at:
https://brainly.com/question/30501511
#SPJ1
someone please help me

Answers

Which is a complete list of factors of each term in the expression 15 + 20x?
Answers
Answer: A
Step-by-step explanation:
what is the direction of the cross product ?
a. x direction
b. -x direction c.y direction d.-y direction e.z direction f.-z direction
Answers
The direction of the cross product is perpendicular to both of the vectors being multiplied. So, the answer to the question of what is the direction of the cross product could be any of the six options provided (x direction, -x direction, y direction, -y direction, z direction, -z direction), depending on the orientation of the vectors being multiplied.
The direction of the cross product is determined by the right-hand rule. When you have two vectors, A and B, the cross product (A x B) will be perpendicular to both A and B in a third direction. To find this direction, point your fingers in the direction of vector A, and then curl them towards vector B. Your thumb will point in the direction of the cross product. The options you provided (x, -x, y, -y, z, -z) depend on the specific vectors you are working with. In general, the cross product direction will be in the z direction or -z direction for vectors lying in the xy plane.
To learn more about cross product click here: brainly.com/question/29097076
#SPJ11
Mhanifa please help this is due soon
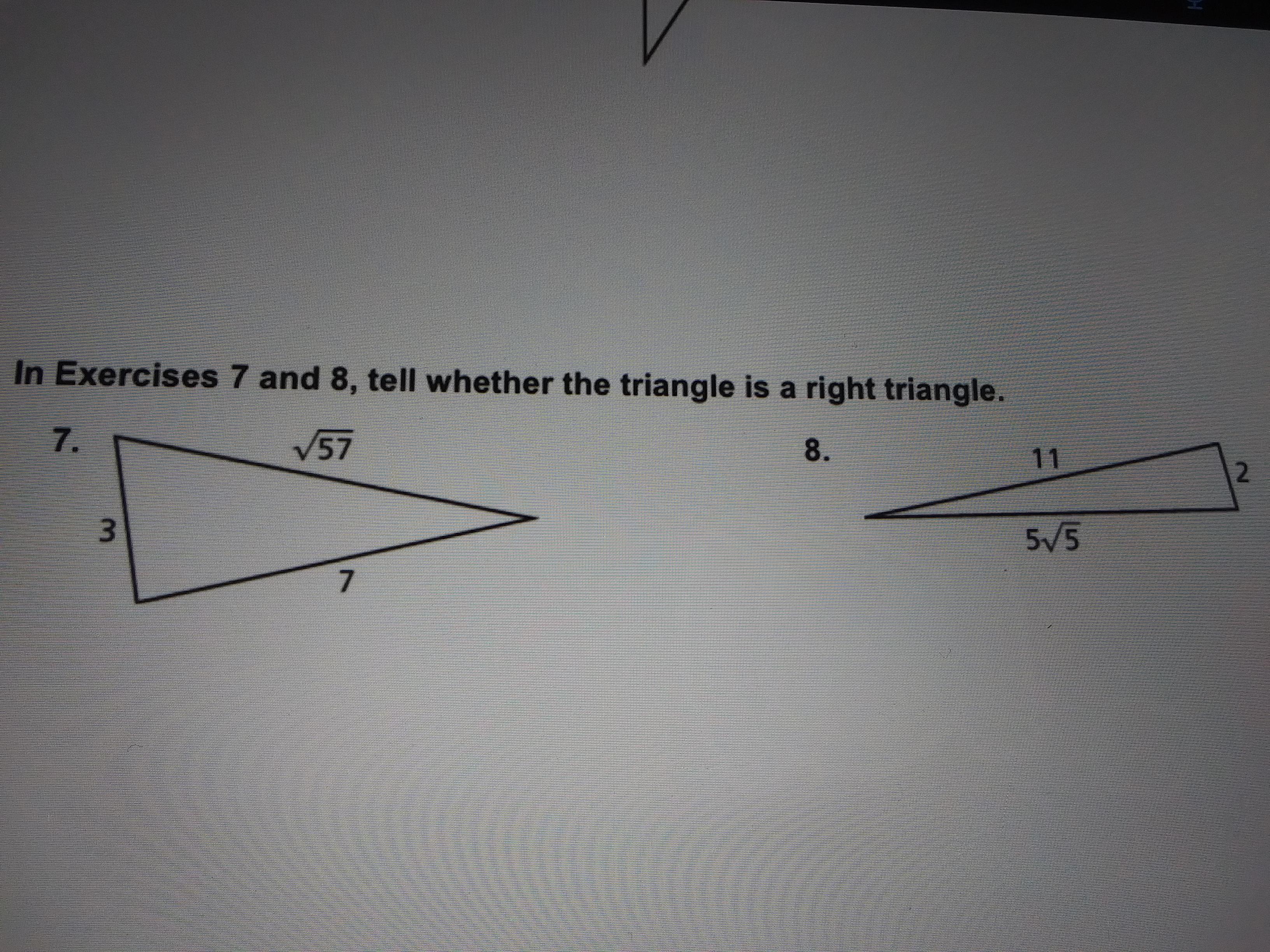
Answers
Answer:
Use Pythagorean theorem:
a² + b² = c²#7
3² + 7² = 9 + 49 = 58 (√57)² = 5758 ≠ 57No#8
11² + 2² = 121 + 4 = 125(5√5)² = 25*5 = 125125 = 125YesAccording to a study done by the Gallup organization, the proportion of Americans who are satisfied with the way things are going in their lives is 0. 82.
a. Suppose a random sample of 100 Americans is asked, "Are you satisfied with the way things are going in your life?" Is the response to this question qualitative or quantitative? Explain.
A. The response is qualitative because the responses can be classified based on the characteristic of being satisfied or not.
B. The response is quantitative because the responses can be classified based on the characteristic of being satisfied or not.
C. The response is quantitative because the responses can be measured numerically and tho values added or subtracted, providing meaningful results
D. The response is qualitative because the response can be measured numerically and the value added or subtracted, providing meaningful results.
b. Explain why the sample proportion, p, is a random variable. What is the source of the variability?
c. Describe the sampling distribution of p, the proportion of Americans who are satisfied with the way things are going in their life. Be sure to verify the model requirements.
d. In the sample obtained in part (a), what is the probability the proportion who are satisfied with the way things are going in their life exceeds 0. 85?
e. Would it be unusual for a survey of 100 Americans to reveal that 75 or fewer are satisfied with the way things are going in their life? Why?
Answers
A. The response is qualitative because the responses can be classified based on the characteristic of being satisfied or not.
B. The source of the variability is due to chance or sampling error, which arises from taking a sample instead of surveying the entire population.
C. The sampling distribution of p is approximately normal.
D. We find that the probability is 0.0912 or about 9.12%.
E. We get:z = (0.75 - 0.82) / sqrt[0.82(1-0.82)/100] = -2.29
a. The response is qualitative because the responses can be classified based on the characteristic of being satisfied or not.
b. The sample proportion, p, is a random variable because it varies from sample to sample. The source of the variability is due to chance or sampling error, which arises from taking a sample instead of surveying the entire population.
c. The sampling distribution of p is approximately normal if the sample size is sufficiently large and if np ≥ 10 and n(1-p) ≥ 10, where n is the sample size and p is the population proportion. In this case, we have:
Sample size (n) = 100
Population proportion (p) = 0.82 Thus, np = 82 and n(1-p) = 18, both of which are greater than 10. Therefore, the sampling distribution of p is approximately normal.
d. To calculate the probability that the proportion who are satisfied with the way things are going in their life exceeds 0.85, we need to find the z-score and then look up the corresponding probability from the standard normal distribution table. The formula for the z-score is:
z = (p - P) / sqrt[P(1-P)/n]
where p is the sample proportion, P is the population proportion, and n is the sample size. Substituting the given values, we get:
z = (0.85 - 0.82) / sqrt[0.82(1-0.82)/100] = 1.33
Looking up the corresponding probability from the standard normal distribution table, we find that the probability is 0.0912 or about 9.12%.
e. Yes, it would be unusual for a survey of 100 Americans to reveal that 75 or fewer are satisfied with the way things are going in their life. To check if it is unusual or not, we need to calculate the z-score and find its corresponding probability from the standard normal distribution table. The formula for the z-score is:
z = (p - P) / sqrt[P(1-P)/n]
where p is the sample proportion, P is the population proportion, and n is the sample size. Substituting the given values, we get:
z = (0.75 - 0.82) / sqrt[0.82(1-0.82)/100] = -2.29
Looking up the corresponding probability from the standard normal distribution table, we find that the probability is 0.0106 or about 1.06%. Since this probability is less than 5%, it would be considered unusual to observe 75 or fewer Americans being satisfied with the way things are going in their life.
Learn more about distribution from
https://brainly.com/question/23286309
#SPJ11
A sample of size n=92 is drawn from a normal population whose standard deviation is σ=6.5. The sample mean is
x
ˉ
=46.17. Parte: Part 1 of 2 (a) Construct un 80% confidence interval for μ. Round the answer to at least two decimal places. An 80% confidence interval for the mean is
Answers
We are 80% confident that the true population mean falls within this interval based on the given sample data. To construct an 80% confidence interval for the population mean (μ), we can use the formula:
Confidence Interval = x ± Z * (σ/√n) Where:
x is the sample mean (46.17)
Z is the Z-score corresponding to the desired confidence level (80% confidence level corresponds to a Z-score of 1.28)
σ is the population standard deviation (6.5)
n is the sample size (92)
Substituting the given values into the formula, we get:
Confidence Interval = 46.17 ± 1.28 * (6.5/√92)
Calculating the expression inside the parentheses first:
6.5/√92 ≈ 0.679. Then, plugging it back into the formula:
Confidence Interval = 46.17 ± 1.28 * 0.679
Calculating the product of 1.28 and 0.679: 1.28 * 0.679 ≈ 0.868
Finally, the confidence interval is: Confidence Interval = 46.17 ± 0.868
Rounding to two decimal places: Confidence Interval ≈ (45.30, 47.04)
Therefore, the 80% confidence interval for the population mean (μ) is approximately (45.30, 47.04).
Learn more about mean here: brainly.com/question/31101410
#SPJ11
Fill in the table using this function rule. y=5+3x M 4 7

Answers
all you have to do is substitute all the Xs to and get a final y output.
for example:
if we take the number x is -1 all you do is:
y=-4(-1)+2
y=4+2
y=6
Help with this math question. It’s phythagorean theorem im pretty sure, but please show working out. Once completed, you’ll have 25 points.

Answers
Answer:
80 degrees
Step-by-step explanation:
The sum of the interior angles of any quadrilateral is 360 degrees. Adding up the known measures gives you 95 + 123 + 62 = 280. Then you can subtract that from 360. 360 - 280 = 80. So x has to be 80 degrees.
After watching Donald Duck in Mathmagic Land, please type out three things that you learned from the video. Did you like the video? Why or why not? Please answer all parts to the question
Answers
Answer:
Hope this helps
Step-by-step explanation:
Mathmagic Land had taught me more about math that I never knew before. I learned that everything can be involved with math. It all starts at the Pythagoreans which were the Greek. An example of how math is used today, is by playing billiards.
In billiards, you have to have a good technique of how your going to hit the ball, (good angles,) and you have to have a precise calculation of the angle your going to hit it at.I also learned when you cut shapes like a sphere, it just makes more and more shapes.
This is what I learned watching the Mathmagic Land Video.
Yes, Donald Duck in Mathmagic Land taught me alot of things I did not know before.
Given f(x) = 3x - 4, find f(5). Write your answer as a number.
Answers
F(5) means replace x with 5 then solve:
3x-4 = 3(5)-4 = 15-4 = 11
F(5) = 11
Can someone please help me with math.

Answers
Answer:
A. B.
Step-by-step explanation:
ALGEBRA 1:
FIND THE PRODUCT OF THE FOLLOWING:
(x^2+2)(5x+1)
please somebody help me, if you’re correct i’ll give you an extra 50 points for helping. please do not use my question for points as i am failing and truly need help i’m so stressed lol.
Answers
use the distribution method
=5x^3+x^2+10x+2
You burn a log on a fire. You use the fire to warm yourself and to light up the
room to read a book. Which energy transformation is taking place?
O A. Thermal energy is transformed to light energy and chemical
energy
B. Chemical energy is transformed to nuclear energy and thermal
energy
C. Nuclear energy is transformed to potential energy and thermal
energy.
D. Chemical energy is transformed to light energy and thermal
energy.

Answers
: D. Chemical energy is transformed to light and thermal energy
(a) Find the values of z, zER, for which the matrix
x3 x
9 1
has inverse (marks-2 per part)
x=
x=
x=
(b) Consider the vectors - (3,0) and 7- (5,5).
(i.) Find the size of the acute angle between i and ü. Angle-
(ii). If -(k, 3) is orthogonal to , what is the value of ke k [2 marks]
(c) Let J be the linear transformation from R2 R2 which is a reflection in the horizontal axis followed by a scaling by the factor 2.
(i) If the matrix of J is W y 1₁ what are y and z
y= [2 marks]
z= [2 marks] U N || 62 -H 9 has no inverse. [6 marks-2 per part] [2 marks]
(d) Consider the parallelepiped P in R³ whose adjacent sides are (0,3,0), (3, 0, 0) and (-1,1, k), where k € Z. If the volume of P is 180, find the two possible values of k. [4 marks-2 each]
k=
k=
(e) Given that the vectors = (1,-1,1,-1, 1) and =(-1, k, 1, k, 8) are orthogonal, find the magnitude of . Give your answer in surd form. [3 marks]
v=
Answers
(a) To find the values of z for which the matrix does not have an inverse, we can set up the determinant of the matrix and solve for z when the determinant is equal to zero.
The given matrix is:
|x3 x|
|9 1|
The determinant of a 2x2 matrix can be found using the formula ad - bc. Applying this formula to the given matrix, we have:
Det = (x3)(1) - (9)(x) = x3 - 9x
For the matrix to have an inverse, the determinant must be non-zero. Therefore, we solve the equation x3 - 9x = 0:
x(x2 - 9) = 0
This equation has two solutions: x = 0 and x2 - 9 = 0. Solving x2 - 9 = 0, we find x = ±3.
So, the values of x for which the matrix has no inverse are x = 0 and x = ±3.
(b) (i) To find the size of the acute angle between the vectors (3,0) and (5,5), we can use the dot product formula:
u · v = |u| |v| cos θ
where u and v are the given vectors, |u| and |v| are their magnitudes, and θ is the angle between them.
Calculating the dot product:
(3,0) · (5,5) = 3(5) + 0(5) = 15
The magnitudes of the vectors are:
|u| = sqrt(3^2 + 0^2) = 3
|v| = sqrt(5^2 + 5^2) = 5 sqrt(2)
Substituting these values into the dot product formula:
15 = 3(5 sqrt(2)) cos θ
Simplifying:
cos θ = 15 / (3(5 sqrt(2))) = 1 / (sqrt(2))
To find the acute angle θ, we take the inverse cosine of 1 / (sqrt(2)):
θ = arccos(1 / (sqrt(2)))
(ii) If the vector (-k, 3) is orthogonal to (5,5), it means their dot product is zero:
(-k, 3) · (5,5) = (-k)(5) + 3(5) = -5k + 15 = 0
Solving for k:
-5k = -15
k = 3
So, the value of k is 3.
(c) Let J be the linear transformation from R2 to R2 that reflects points in the horizontal axis and then scales them by a factor of 2. The matrix of J can be found by multiplying the reflection matrix and the scaling matrix.
The reflection matrix in the horizontal axis is:
|1 0|
|0 -1|
The scaling matrix by a factor of 2 is:
|2 0|
|0 2|
Multiplying these two matrices:
J = |1 0| * |2 0| = |2 0|
|0 -1| |0 2| |0 -2|
So, the matrix of J is:
|2 0|
|0 -2|
Therefore, y = 2 and z = -2.
(d) The volume of a parallelepiped can be found by taking the dot product of two adjacent sides and then taking the absolute value of the result.
The adjacent sides of the parallelepiped P are (0,3,0)
To learn more about scaling matrix click here : brainly.com/question/16662440
#SPJ11
why is it important to be able to calculate percentages?
Answers
Answer:
We use percentages to make calculations easier. It is much simpler to work with parts of 100 than thirds, twelfths and so on, especially because quite a lot of fractions do not have an exact (non-recurring) decimal equivalent.
Step-by-step explanation:
3] Question 5 Consider the vector field F(x, y, z) = y cos (xy) i + x cos (xy)j – sin zk. (i) Calculate the curl of the vector field F. State whether F is conservative. (ii) Let C be the curve joining the origin (0,1,-1) to the point with coordinates (1, 2V2,2) defined by the following parametric curve r(t) = n* i + t}j + tcos atk, 15t52. Calculate the scalar line integral of the vector field. F. dr. F.dr.
Answers
Given vector field, F(x, y, z) = y cos (xy) i + x cos (xy) j – sin z k To calculate the curl of F, we need to take the curl of each component and subtract as follows,∇ × F = ( ∂Q/∂y - ∂P/∂z ) i + ( ∂P/∂z - ∂R/∂x ) j + ( ∂R/∂x - ∂Q/∂y ) k...where P = y cos(xy), Q = x cos(xy), R = -sin(z)
Now we calculate the partial derivatives as follows,
∂P/∂z = 0, ∂Q/∂y = cos(xy) - xy sin(xy), ∂R/∂x = 0...
and,
∂P/∂y = cos(xy) - xy sin(xy), ∂Q/∂z = 0, ∂R/∂y = 0
Therefore,
∇ × F = (cos(xy) - xy sin(xy)) i - sin(z)j
The curl of F is given by:
(cos(xy) - xy sin(xy)) i - sin(z)j.
To state whether F is conservative, we need to determine if it is a conservative field or not. This means that the curl of F should be zero for it to be conservative. The curl of F is not equal to zero. Hence, the vector field F is not conservative. Let C be the curve joining the origin (0,1,-1) to the point with coordinates (1, 2V2,2) defined by the following parametric curve:
r(t) = n* i + t}j + tcos atk, 15t52.
The curve C is defined as follows,r(t) = ni + tj + tk cos(at), 0 ≤ t ≤ 1Given vector field, F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk Using the curve parameterization, we get the line integral as follows,∫CF.dr = ∫10 F(r(t)).r'(t)dt...where r'(t) is the derivative of r(t) with respect to t
= ∫10 [(t cos(at))(cos(n t)) i + (n cos(nt))(cos(nt)) j + (-sin(tk cos(at)))(a sin(at)) k] . [i + j + a tk sin(at)] dt
= ∫10 [(t cos(at))(cos(n t)) + (n cos(nt))(cos(nt)) + (-a t sin(at) cos(tk))(a sin(at))] dt
= ∫10 [(t cos(at))(cos(n t)) + (n cos(nt))(cos(nt)) - a^2 (t/2) (sin(2at))] dt
= [sin(at) sin(nt) - (a/2) t^2 cos(2at)]0^1
= sin(a) sin(n) - (a/2) cos(2a)
The vector field F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk is given. Firstly, we need to calculate the curl of F. This involves taking the curl of each component of F and subtracting. After calculating the partial derivatives of each component, we get the curl of F as (cos(xy) - xy sin(xy)) i - sin(z)j. Next, we need to determine whether F is conservative. A conservative field has a curl equal to zero. As the curl of F is not equal to zero, it is not a conservative field. In the second part of the problem, we have to calculate the scalar line integral of the vector field F. dr along the curve C joining the origin to the point with coordinates (1, 2V2, 2). We use the curve parameterization to calculate the line integral. After simplifying the expression, we get the answer as sin(a) sin(n) - (a/2) cos(2a).
The curl of the given vector field F(x, y, z) = y cos(xy) i + x cos(xy)j – sin zk is (cos(xy) - xy sin(xy)) i - sin(z)j. F is not conservative as its curl is not zero. The scalar line integral of the vector field F along the curve C joining the origin to the point with coordinates (1, 2V2,2) is sin(a) sin(n) - (a/2) cos(2a).
To learn more about curve parameterization visit:
brainly.com/question/12982907
#SPJ11
Use the image to answer the question.
С
(x-2)
(2x - 3)
B
(3x-427
D
А
What is the measure of
Answers
I need help with these, this will be split up in parts. I know this is asking for a lot and I'm sorry





Answers
1.
Collinear : Points on the same line
Non-collinear: Points not on same line
Line: All points between any two points extending in opposite directions.
Space: Where things exist
Coplaner: Points and lines on the same plane
Geometry: Earth measure
Plane: A flat surface
Non-coplaner: Points and lines not on the same plane
2. EF
3. EGD
4. AD
5. G
