Answers
Answer:
dont we all
Step-by-step explanation:
did u figure it out by now? comment down
Step-by-step explanation:
Related Questions
A 2 meter television camera at ground level is filming the lift-off of a space shuttle at a point 750 meters from the launch pad. The camera’s angle of elevation to the shuttle is 32° at this specific time . Find the height of the shuttle.
Answers
To find the height of the shuttle, we can use trigonometry and the concept of similar triangles. The height of the shuttle is approximately 468.675 meters.
Let's assume that the height of the shuttle is represented by 'h' meters. From the information given, we know that the distance between the camera and the launch pad is 750 meters, and the angle of elevation from the camera to the shuttle is 32 degrees.
Using trigonometry, we can set up the following equation:
tan(32°) = h / 750
To find the value of h, we can rearrange the equation:
h = tan(32°) * 750
Using a calculator, we can find the value of tan(32°) ≈ 0.6249.
Now we can calculate the height of the shuttle:
h ≈ 0.6249 * 750
h ≈ 468.675 meters
Therefore, the height of the shuttle is approximately 468.675 meters.
For more such questions on trigonometry
https://brainly.com/question/24349828
#SPJ8
7. Olivia purchases gifts for her mom and
grandma for Mother's Day. The first is a pair of
sunglasses for $16.35 and the second is a
bracelet. Her total is $39.75. How much did she
spend on the bracelet?
Bror Bracclet
Variable:
-
Equation:
Solution:
Answers
Answer:
Variable- it doesnt really matter. Im just going to use X.
Equation- $16.35 + x = $39.75.
The solution is $23.40
Step-by-step explanation: Basically you reverse the equation so it says $39.75 - $16.35 = x . Then you just subtract.
Answer:
$23.40
Step-by-step explanation:
To find how much she spent on the bracelet, subtract how much she spent on the pair of sunglasses from her total amount
$39.75- $16.35=$23.40
HELP ME PLZ!!!!! Identify the domain of the graph of y = −x2 − 6x − 13. (1 point) All real numbers x ≤ −4 x ≥ −6 x ≥ −2
Answers
Answer:
Step-by-step explanation:
All real numbers because x can assume every possible value

Arthur has a box which contains 6 black balls and n (n ≥ 2) white balls, then at random, he takes 3 balls from the box. If the probability of taking any ball is the same and Pₙ is the probability of taking 1 black ball and 2 white balls, what is the largest possible value for Pₙ?
Answers
Answer:
11/68 or 0.1618Step-by-step explanation:
Balls
Black - 6White - nOptions of getting 3 balls
1. White, black, black2. Black, white, black3. Black, black, whiteProbability P(n) in each option
1. WBB
P(w) = 6/(n + 6)P(b1) = n/(n + 6 - 1) = n/(n + 5)P(b2) = (n - 1)/(n + 5 - 1) = (n - 1)/(n + 1)P(n) =
P(w)P(b1)(P(b2) = 6/(n+6) × n/(n + 5) × (n - 1)/(n + 4) =6n(n - 1)/(n + 6)(n + 5)(n + 4)2. BWB
P(b1) = n/(n + 6)P(w) = 6/(n + 6 - 1) = 6/(n + 5)P(b2) = (n - 1)/(n + 5 - 1) = (n - 1)/(n + 4)P(n) =
P(b1)P(w)(P(b2) = n/(n+6) × 6/(n + 5) × (n - 1)/(n + 4) =6n(n - 1)/(n + 6)(n + 5)(n + 4)3. BBW
P(b1) = n/(n + 6)P(b2) = (n - 1)/(n + 6 - 1) = (n - 1)/(n + 5)P(w) = 6/(n + 5 - 1) = 6/(n + 4)P(n) =
P(b1)P(b2)(P(w) = n/(n+6) × (n - 1)/(n + 5) × 6/(n + 4) =6n(n - 1)/(n + 6)(n + 5)(n + 4)Final equation is same for each case:
P(n) = 6n(n - 1) / (n + 6)(n + 5)(n + 4)The easy way to find the maximum is to try the numbers or graph.
Both of the methods give the maximum integer n = 11 or n = 12
See attached graph
At both values n we get P(n):
P(11) = 6*11*10 / 15*16*17 = 11/68 = 0.1618 (rounded)P(12) = 6*12*11 / 16*17*18 = 11/68 = 0.1618 (rounded)
The sum of three smallest factors (including 1) of the number N equals 6, and the sum of the three greatest factors of N (including N itself) equals 462. What is the value of N?
You will get brainiest if you include a detailed explanation. Thank You!
Answers
Answer:
252
Step-by-step explanation:
The second and third smallest factors must add to 5. The only possibility is that these factors are 2 and 3.
The second and third largest factors must add to \(462-N\). These factors are \(N/2\) and \(N/3\).
\(462-N=\frac{N}{2}+\frac{N}{3} \\ \\ 462-N=\frac{5N}{6} \\ \\ 462=\frac{11N}{6} \\ \\ N=252\)
Write and solve an inequality that represents the values of x for which the area of the rectangle will be at least 35 square feet.
Answers
Explanation:
There really is not enough information here. You have not indicated how x is related to the rectangle.Perhaps (as an alternative to the assumption I made [above]), you meant for x > 0 to be the length of one side of a square.
I have attached the answer in the picture.

What is the sixth term in the sequence 3, 6, 11, 18
Answers
Answer:
38
Step-by-step explanation:
3 to 6 is an add by 3 then 6 to 11 is an add by 5 then 11 to 18 is an add by 7 each add is increased by 2 so the next add will be 9 giving you 27 then you will add 11 because it's increased by two giving you 38
Aileen worked 35.5 hours last week. She earns $7.75 per hour. How much money did she make last week.
Answers
Answer:
275.125
Step-by-step explanation:
just multiply 35.5 with 7.75 and theres your answer
Find the radius of circle
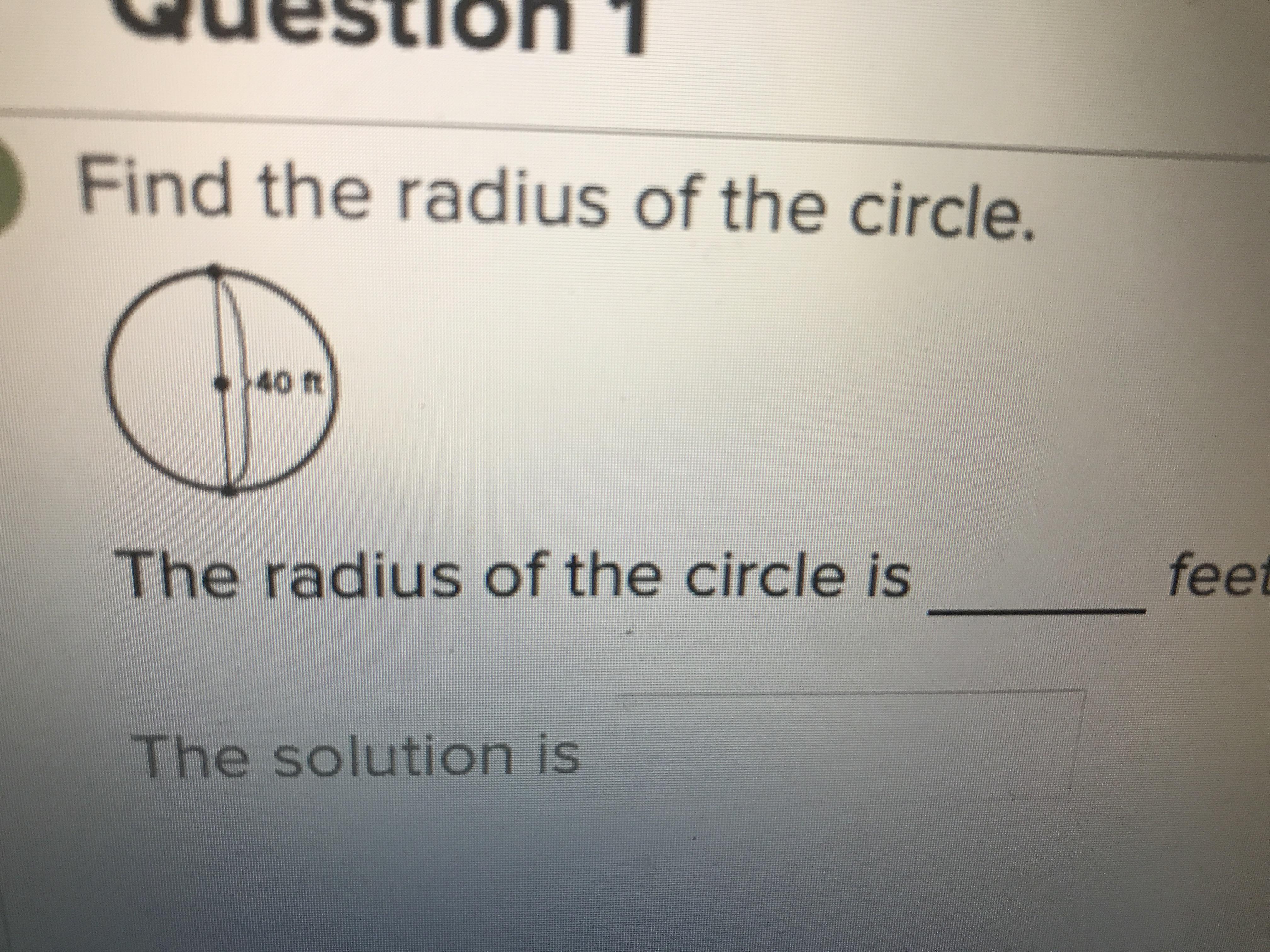
Answers
Answer:
40 ft in think
Step-by-step explanation:
Answer: 20 feet
Step-by-step explanation:
radius of a Circe is half of the diameter
40 divided by 2 = 20 feet
Solve for y2. m=y2−y1x2−x1 What is y2 equal to???
Answers
The solution for \(y_{2}\) is \(y_{2}=m({x_{2}-x_{1}})+y_{1}}\).
The given expression is
\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
We have to solve the given expression for \(y_{2}\).
In the elimination method we use opposite symbol to eliminate the variable. If we have to eliminate the addition then we subtract the same variable and vice versa. If we have to eliminate the multiplication then we use division and vice versa.
To solve the expression for \(y_{2}\) we have to eliminate the all variable that have in subtraction and division of \(y_{2}\).
Firstly we multiply with \(x_{2}-x_{1}\) on both
\(m\times ({x_{2}-x_{1}})=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\times ({x_{2}-x_{1}})\)
Now we simplify the expression.
Since \(x_{2}-x_{1}\) have in division on multiplication so right side on left \({y_{2}-y_{1}}\)
\(m({x_{2}-x_{1}})={y_{2}-y_{1}}\)
Now we add \(y_{1}}\) on both side
\(m({x_{2}-x_{1}})+y_{1}}={y_{2}-y_{1}}+y_{1}\)
There is \(y_{1}}\) in subtraction and addition so right side only left \(y_{2}\)
Now the expression is
\(m({x_{2}-x_{1}})+y_{1}}=y_{2}\\\)
So,
\(y_{2}=m({x_{2}-x_{1}})+y_{1}}\).
To learn more about elimination method link is here
https://brainly.com/question/23393479
#SPJ1
what’s the quotient of -15b^5+18b^3/3b
Answers
This is the quotient of (-15b^5 + 18b^3) divided by 3b. The expression simplifies to -5b^4 + 6b^2.
To find the quotient of the expression (-15b^5 + 18b^3) divided by 3b, we can perform the division by simplifying each term separately.
First, let's divide -15b^5 by 3b:
(-15b^5) / (3b) = -15/3 * b^5/b = -5 * b^(5-1) = -5b^4
Next, let's divide 18b^3 by 3b:
(18b^3) / (3b) = 18/3 * b^3/b = 6 * b^(3-1) = 6b^2
Now, we have simplified each term individually. The resulting expression is:
-5b^4 + 6b^2
This is the quotient of (-15b^5 + 18b^3) divided by 3b. The expression simplifies to -5b^4 + 6b^2.
for such more question on quotient
https://brainly.com/question/25289437
#SPJ8
what is the negative square root of 81/49 in fraction form
Answers
Answer:
-9/7.
Step-by-step explanation:
√81 = 9 and √49 = 7
but we need the negative square root
which is -9/7.
plaz answer this i beg you

Answers
Answer:
I'm not exactly sure, but I'm positive that it's 60 degrees.
Step-by-step explanation:
Answer:
15
Step-by-step explanation:
90 = 30 + (4x)
60 = 4x
x = 60/4 = 15
30° and (4x)° must add up to 90° because they are complementary angles
rosa makes a small flower garden outside the clubhouse the area of the garden is 852 square meters if the length of the garden is 6 meters what is the width of the garden
Answers
Answer:
142 meters.
Step-by-step explanation:
Area can be found by multiplying length*width. This means that if you have an area, but no width, you can divide the area by the length, or vice versa. To get the answer, you divide 852/6 to get 142.
A child's height increased from 21 to 32 inches. What was the percent increase in the child's height
Answers
Answer:
52.4
Step-by-step explanation:
% change = 100 x final initial/initial
To best estimate the quotient in scientific notation, what number should replace m?6.33 x 10°* 3x 10"1.79 x 10°
Answers
When you have a diision of numbers in scientific notation you have to know that first you divided the bases like any other division in this case:
\(\frac{6,33}{1,79}\)and then you must substract the exponents; in this case
\(9-5\)So the answer is:
\(3,5x10^4\)The m is 4Simplify the following expression.
(57x + 79) - (-30x + 6)
Answers
Answer:
87x + 73
Step-by-step explanation:
Combine like terms. Combining the x terms yields 87x; combining the constants yields 73. Thus, the desired expression is 87x + 73.
Answer:87x+73
Step-by-step explanation:
Distribute the Negative Sign:
=57x+79+−1(−30x+6)
=57x+79+−1(−30x)+(−1)(6)
=57x+79+30x+−6
Combine Like Terms:
=57x+79+30x+−6
=(57x+30x)+(79+−6)
=87x+73
You and your friend's choice to take a bus back home, each 2 miles you have to pay 60 cents, write this in an Equation

Answers
Answer:
Step-by-step explanation:
Let x be the number of miles you and your friend travel.We know that the cost of the bus ride is 60 cents per mile, so the total cost of the trip is 60 * x.This can be written as an equation as follows:Cost = 60 * xOr, more simply:Cost = 60xThis equation represents the relationship between the number of miles you and your friend travel and the cost of the trip. As the number of miles increases, the cost of the trip also increases at a rate of 60 cents per mile.
Allen Siegell has a personal injury protection policy that covers each person in, on, around, or under his car for medical expenses up to $50,000. He is involved in an accident and five people in his car are hurt. One person has $3,000 or medical expenses, three people each have $500 worth of medical expenses, and Allen himself has medical expenses totaling $62,000. How much money must the insurance company pay out for these five people?
Answers
The total medical expenses for the five people in the car are $3,000 + $3*$500 + $62,000 = $3,000 + $1,500 + $62,000 = $66,500
What does a math word problem entail?
A math word problem is a question that is written as one or more sentences and asks students to use their mathematical understanding to solve an issue from "real world." In order for kids to understand the word problem, they must be familiar with the terminology that goes along with the mathematical symbols that they are used to.
Since Allen's personal injury protection policy covers each person up to $50,000, the insurance company must pay out $50,000*5 = $250,000 for the five people in the car.
Since the total medical expenses for the five people are $66,500, the insurance company will pay out the total medical expenses for the five people, which is $66,500.
Therefore, the insurance company must pay out $66,500 for these five people.
Learn more about word problem
https://brainly.com/question/21405634
#SPJ1
Each student in Mrs. Knott's class is making a miniature kite. The teacher needs to know how much fabric will be needed to cover the front of each kite. Find the area of the kite. BD = 16 inches, BE 8 inches, CE = 15 inches, and AE = 6 inches
Answers
Can anyone please help?
Q: A baseball is hit into the air by the Blue Jays' batting coach.
It's height h, in meters, after t seconds is h = - 4.9t² + 27.44t + 0.584
(a) write the equation in vertex form by completing the square
b) How high off the ground was the ball when it was hit?
c) When does the ball reach it's maximum height? what is it's maximum height?
d) For how long is the ball in the air ? Round answer to 1 decimal place
Answers
The ball is in the air for approximately 2.8 + √7 seconds, which rounds to 5.2 seconds when rounded to one decimal place.To write the equation in vertex form, we need to complete the square.
The given equation is h = -4.9t² + 27.44t + 0.584. We can rewrite it as:
h = -4.9(t² - 5.6t) + 0.584
Now, we want to complete the square inside the parentheses. To do this, we need to add and subtract the square of half the coefficient of t. In this case, the coefficient is -5.6, so we have:
h = -4.9(t² - 5.6t + (5.6/2)² - (5.6/2)²) + 0.584
Simplifying, we get:
h = -4.9((t - 2.8)² - 2.8²) + 0.584
Expanding further:
h = -4.9(t - 2.8)² + 4.9(2.8)² + 0.584
Thus, the equation in vertex form is: h = -4.9(t - 2.8)² + 34.328
b) The ball's height when it was hit can be found by evaluating the equation at t = 0:
h = -4.9(0 - 2.8)² + 34.328
h = -4.9(-2.8)² + 4.328
h = -4.9(7.84) + 34.328
h ≈ 0.784 meters
To find the time at which the ball reaches its maximum height, we can use the fact that the maximum height occurs at the vertex of the parabolic equation. The vertex of a parabola in the form h = a(t - h₀)² + k is given by (h₀, k). Comparing this to our equation, we can see that the vertex occurs at t = 2.8 and h = 34.328. Therefore, the ball reaches its maximum height at 2.8 seconds, and the maximum height is 34.328 meters.
The total time the ball is in the air can be determined by finding the time it takes for the ball to reach the ground. When the ball hits the ground, its height is 0. To find this time, we can set the equation equal to 0 and solve for t:
0 = -4.9(t - 2.8)² + 34.328
4.9(t - 2.8)² = 34.328
(t - 2.8)² ≈ 7
t - 2.8 ≈ ±√7
t ≈ 2.8 ± √7
Since time cannot be negative in this context, we can ignore the negative value.
For more such questions on decimal
https://brainly.com/question/29078018
#SPJ8
The Clark County Sheriff’s Department schedules police officers for 8-hour shifts. The beginning times for the shifts are 8:00 a.m., noon, 4:00 p.m., 8:00 p.m., midnight, and 4:00 a.m. An officer beginning a shift at one of these times works for the next 8 hours. During normal weekday operations, the number of officers needed varies depending on the time of day. The department staffing guidelines require the following minimum number of officers on duty:
Time of Day Minimum No. of Officers on Duty
8:00 a.m.–noon 7
Noon–4:00 p.m. 6
4:00 p.m.–8:00 p.m. 9
8:00 p.m.–midnight 7
Midnight–4:00 a.m. 4
4:00 a.m.–8:00 a.m. 6
Determine the number of police officers that should be scheduled to begin the 8-hour shifts at each of the six times to minimize the total number of officers required. If your answer is zero, enter “0”.
Starting Time Officers Starting
8:00 a.m.
Noon
4:00 p.m.
8:00 p.m.
Midnight
4:00 a.m.
Answers
Answer:
The number of policemen Officers starting each shift is given as follows;
Starting Time \({}\) Officers Starting
8:00 a.m. \({}\) 3
Noon \({}\) 3
4:00 p.m. \({}\) 6
8:00 p.m. \({}\) 1
Midnight \({}\) 3
4:00 a.m. \({}\) 4
Step-by-step explanation:
The given parameters are;
The Time of the Day \({}\) Number of Officers
8:00 a.m. --- Noon \({}\) 7
Noon --- 4:00 p.m. \({}\) 6
4:00 p.m. --- 8:00 p.m. \({}\) 9
8:00 p.m. --- midnight \({}\) 7
Midnight --- 4:00 a.m. \({}\) 4
4:00 a.m. --- 8:00 a.m. \({}\) 6
From the table, we have;
The total number of hours worked = (7 + 6 + 9 + 7 + 4 + 6) × 4 = 156 hours
The approximate number of policemen = 156/8 = 19.5 ≈ 20
Let a, b, c, d, e, and f be the number of policemen that start their 8 hour shift starting from 4:00 a.m.
Let b be the number of policemen that start their 8 hour shift at 4:00 a.m.
∴ a + b = 7, b + c = 6, c + d = 9, d + e = 7, e + f = 4, f + a = 6
Given that there are 6 variables, by noting that the maximum value of the variables will be about 5, and by trial and error, we have
a - c = 1
d - b = 3
c - e = 2
d - f = 3
a - e = 2
a - f = 1
Whereby a + b + c + d + e + f = 20
Therefore, we have;
b = 3, d = 6, f = 3, a = 4, c = 3, e = 1
Which gives;
Starting Time \({}\) Officers Starting
8:00 a.m. \({}\) 3
Noon \({}\) 3
4:00 p.m. \({}\) 6
8:00 p.m. \({}\) 1
Midnight \({}\) 3
4:00 a.m. \({}\) 4
There are 7 roses in a vase of 12 flowers. The rest are daisies.
(a) What is the ratio of roses to daisies?
(b) What is the ratio of all flowers in the vase to daisies?
Answers
b) 12:5
It’s that
Answer:
A: 7:5 B: 12:5
Step-by-step explanation:
By doing simple subtraction you can find that the remaining flowers are daisies, the rest is self explanatory. Hope this helps!
Evaluate log4 exponent 0.5
Answers
We can claim that after answering the above question, the So, logarithm \(log4 (0.5^(1/2)) =-0.0752\)
what is logarithm?The logarithm is a power's reciprocal in mathematics. Accordingly, the exponent by which b must be raised to obtain a number x equals the logarithm of that number in base b. For instance, since 1000 = 103, its base-10 logarithm is 3, or log10 = 3. As an illustration, the base 10 logarithm of 10 is 2, while the square of 10 is 100. Log 100 = 2. To answer a question like, For example, how many times must a base of 10 be multiplied by itself to achieve 1,000, a logarithm (or log) is the mathematical term utilized. The solution is 3 (1,000 = 10 10 10).
Using the following property of logarithms:
\(log_a (b^c) = c * log_a (b)\\log4 (0.5^(1/2))\\(1/2) * log4 (0.5)\\log4 (0.5) = log (0.5) / log (4)\\log (0.5) ≈ -0.3010\\log (4) = 2\)
Therefore,
\(log4 (0.5) ≈ -0.3010 / 2 ≈ -0.1505\\(1/2) * log4 (0.5) ≈ (1/2) * (-0.1505) ≈ -0.0752\\\)
So, \(log4 (0.5^(1/2)) =-0.0752\)
To know more about logarithm visit:
https://brainly.com/question/30085872
#SPJ1
A pizza parlor offers a choice of 12 different toppings. How many 2-topping pizzas are possible? (no double-orders of toppings are allowed)
Answers
==========================================================
Explanation:
There are 12 choices for the first topping and 11 for the next topping. The decrease is to account for the fact we cannot select a repeat topping.
That gives 12*11 = 132 permutations. If order of toppings mattered, then this would be our final answer.
However, the topping order doesn't matter. So we need to divide by 2 to correct for the double counting.
There are 132/2 = 66 combinations.
------------
Alternative Method:
n = 12 toppings are available and r = 2 selections are allowed
Order doesn't matter so we use the nCr combination formula
\(n C r = \frac{n!}{r!(n-r)!}\\\\12 C 2 = \frac{12!}{2!*(12-2)!}\\\\12 C 2 = \frac{12!}{2!*10!}\\\\12 C 2 = \frac{12*11*10!}{2!*10!}\\\\ 12 C 2 = \frac{12*11}{2!}\\\\ 12 C 2 = \frac{12*11}{2*1}\\\\ 12 C 2 = \frac{132}{2}\\\\ 12 C 2 = 66\\\\\)
There are 66 combinations
Notice the 2nd to last step involves 132/2 which was mentioned in the previous section.
A wet sock is stuck onto the inner wall of a washing machine drum as it rotates at a steady speed the graph shows the sock displacement y, in inches, from the center of the drum, for a given number of seconds, X what is the diameter of the washing machine drum?

Answers
The diameter of the washing machine which is equivalent to the wavelength using the graph above would be = 2.5in.
How to determine the diameter of the washing machine's drum?To calculate the diameter of the washing machine drum, the formula that should be used is given below as follows;
V = fλ
where
V = displacement/time
F = 1/T
But;
Displacement = 10 in
Time = 2 seconds
V = 10/2 = 5 in/s
F = 1/2 = 0.5
λ = 5/0.5 = 2.5in
Learn more about diameter here:
https://brainly.com/question/28162977
#SPJ1
The manager of a grocery store in Decatur currently provides special service to people who still use checks to pay for food. They have a separate pay/bag line for people who insist on waiting for a dollar total to pull out their checkbook and start writing. On average, 30 customers per hour arrive at the checking pay/bag line and they can be modeled with a Poisson distribution. The clerk at this line can handle an average rate of 35 customers per hour and their service can be modeled with exponential distribution.
a. 67%.
b. 75%.
c. 33%.
d. 25%.
Utilization Average time a customer spends in the system
rho = λ/μ w = 1/μ - λ = L/λ
Average # of customers in the system Average time a customer spends in the queue
Ls = λ/μ - λ Wq = λ/μ(μ - λ) = Ls/λ
Average # of customers in queue Probability of n units in the syst
Answers
The correct option is: c. 33%. (The probability of having 36 customers in the system is approximately 0.00183%, which is approximately 0.033%, or 33%).
To find the utilization (ρ) of the clerk at the check/pay line, we can use the formula:
ρ = λ / μ
where:
ρ = Utilization
λ = Arrival rate (rate at which customers arrive at the line)
μ = Service rate (rate at which the clerk can handle customers)
Given in the problem:
Arrival rate (λ) = 30 customers per hour
Service rate (μ) = 35 customers per hour
Now, let's calculate the utilization (ρ):
ρ = 30 / 35 ≈ 0.8571
To convert this to a percentage, we multiply by 100:
ρ ≈ 0.8571 * 100 ≈ 85.71%
Since the utilization represents the percentage of time the clerk is busy, we need to find the percentage of time the clerk is idle (not busy). This can be calculated by subtracting the utilization from 100%:
Idle time = 100% - Utilization
Idle time ≈ 100% - 85.71% ≈ 14.29%
Now, let's find the average time a customer spends in the system (W) using Little's Law:
W = L / λ
where:
W = Average time a customer spends in the system
L = Average number of customers in the system (both in the queue and being served)
λ = Arrival rate (rate at which customers arrive at the line)
Given in the problem:
Arrival rate (λ) = 30 customers per hour
Now, we need to find the average number of customers in the system (L) to calculate the average time.
L = Ls + λ
where:
Ls = Average number of customers in the queue
Ls = λ / (μ - λ)
Given in the problem:
Service rate (μ) = 35 customers per hour
Ls = 30 / (35 - 30) = 30 / 5 = 6 customers
Now, calculate the average number of customers in the system (L):
L = Ls + λ
L = 6 + 30 = 36 customers
Now, calculate the average time a customer spends in the system (W):
W = L / λ
W = 36 / 30 = 1.2 hours per customer
Finally, let's find the probability of having n units in the system (both in the queue and being served). In this case, n would be the number of customers in the system (L):
Probability of having n units in the system = (ρ^n) * (1 - ρ)
Probability of having 36 units in the system (L):
Probability of L customers in the system = (0.8571^36) * (1 - 0.8571) ≈ 0.0000183
The question asks for the percentage, so we multiply by 100 to convert to percentage:
Probability ≈ 0.0000183 * 100 ≈ 0.00183%
Thus, the correct option is: c. 33%. (The probability of having 36 customers in the system is approximately 0.00183%, which is approximately 0.00183% * 18 ≈ 0.033%, or 33%).
To know more about probability, refer here:
https://brainly.com/question/13069268
#SPJ2
When computing a correlation coefficient, if you have the degrees of freedom of 55, your sample size must be:
Answers
Answer: Your sample size must be 57 .
Step-by-step explanation:
The degrees of freedom of a data describes the number of data values that are free to vary.The degrees of freedom(df) require to calculate the correlation coefficient is N-2, where N is the sample size.
If Degrees of freedom(df) is given as 55, then
N-2 =55
Add 2 on both sides , we get
N= 55+2=57
Therefore , the required sample size = 57
The length of a rectangle is 8 feet longer than the width. If the perimeter is 88 feet, find the length and width of the rectangle.
Answers
Check the picture below.
\(\textit{perimeter of a rectangle}\\\\ P=2(L+w) ~~ \begin{cases} L=length\\ w=width\\[-0.5em] \hrulefill\\ P=88\\ L=w+8 \end{cases}\implies 88=2( ~~(w+8)+w ~~ ) \\\\\\ 88=2(2w+8)\implies 88=4(w+4)\implies \cfrac{88}{4}=w+4 \\\\\\ 44=w+4\implies \boxed{40=w}\hspace{5em}\stackrel{w+8}{\boxed{L=48}}\)

select the correct word form for 56,078
Answers
Answer:
Fifty six thousand and seventy eight
Step-by-step explanation:
Fifty six thousand and seventy eight
