X2+5xy+6y2 challenge question
Answers
Answer:
Step-by-step explanation:
\(x^2+5xy+6y^2\\ \\ x^2+2xy+3xy+6y^2\\ \\ x(x+2y)+3y(x+2y)\\ \\ (x+3y)(x+2y)\)
Related Questions
Please help I need the answer by today
Use the graph shown to the right to find each of the following.
(a) The x-intercept(s) is/are 1
(Type an ordered pair. Use a comma to separate answers as needed.)
(a) the x-intercept(s), and (b) the zero(s) of the function,
-2

Answers
Answer:
the x intercepts of the parabola are -2.
0=-8m-12m²+24
solve using quadratic formula
Answers
After solving using quadratic equation we get,
x = 1.12 or x = -1.79
Given, 0=-8m-12m²+24
-8m-12m²+24 = 0
8m+12m²-24 = 0
12m²+8m-24 = 0
Now, taking 4 common from the expression
4(3m²+2m-6) = 0
3m²+2m-6 = 0
Now, applying Quadratic Formula
\(x=\frac{-b±\sqrt{b^{2}-4ac } }{2a}\)
x = (-2 ± √4 + 72)/6
x = (-2 ± √76)/6
x = (-2 ± 8.72)/6
x = (-2 + 8.72)/6 or x = (-2 - 8.72)/6
x = 6.72/6 or x = -10.72/6
x = 1.12 or x = -1.79
Hence, x = 1.12 or x = -1.79
Learn more about Quadratic Equations here https://brainly.com/question/1214333
#SPJ1
Which of the binomials below is a factor of this trinomial?
x² + 5x-36

Answers
Answer:
A. x + 9
Step-by-step explanation:
x² + 5x - 36 = (x + 9) (x - 4)
The carrying capacity of a drain pipe is directly proportional to the area of its cross- section. If a cylindrical drain pipe can carry 36 litres per second, determine the percentage increase in the diameter of the drain pipe necessary to enable it to carry 60 litres per second.
Answers
Step-by-step explanation:
Let's start by using the formula for the volume of a cylinder:
V = πr^2h
where V is the volume of the cylinder, r is the radius of the cylinder, h is the height of the cylinder, and π is a mathematical constant (approximately equal to 3.14).
Since we are dealing with a drain pipe, we can assume that the height of the cylinder is fixed and does not change. Therefore, we can rewrite the formula as:
V = πr^2h = Ah
where A is the cross-sectional area of the cylinder.
Now, let's use the given information that the drain pipe can carry 36 litres per second. We know that the volume of water that passes through the pipe in one second is equal to 36 litres. We can therefore write:
36 = Ahv
where v is the velocity of the water flowing through the pipe. Since we are assuming that the height of the cylinder is fixed, we can simplify this equation to:
36 = Av
Now we need to determine the percentage increase in the diameter of the drain pipe necessary to enable it to carry 60 litres per second. Let's call the new diameter d2 and the old diameter d1. We can set up a proportion to solve for d2:
A1/A2 = d1^2/d2^2
We know that A1 and A2 are proportional to the volumes of water the pipe can carry, so we can write:
A1/A2 = 36/60
Simplifying this equation, we get:
A1/A2 = 3/5
Substituting in the formula for the cross-sectional area of a cylinder, we get:
πd1^2/4 / πd2^2/4 = 3/5
Simplifying further, we get:
d1^2/d2^2 = 3/5
Taking the square root of both sides, we get:
d1/d2 = sqrt(3/5)
Now we can solve for d2:
d2 = d1 / sqrt(3/5)
We want to know the percentage increase in the diameter, which we can find using the formula:
% Increase = (New Value - Old Value) / Old Value x 100%
Substituting in our values, we get:
% Increase = (d1 / sqrt(3/5) - d1) / d1 x 100%
Simplifying, we get:
% Increase = (1 / sqrt(3/5) - 1) x 100%
Using a calculator, we get:
% Increase ≈ 34.64%
Therefore, the percentage increase in the diameter of the drain pipe necessary to enable it to carry 60 litres per second is approximately 34.64%.
If A(0, 4), B(5, y), and AB = 13. What is y?
Answers
The required value of y for the given segment AB is given as y = 16, -8.
A line is a straight curve connecting two points or more showing the shortest distance between the initial and final points.
here,
A(0, 4), B(5, y), and AB = 13.
Applying the distance formula,
D = √[[x₂ - x₁]² + [y₂- y₁]²]
Substitue the value in the above expression,
13 = √[[5 - 0]² + [y - 4]²]
169 = 25 + [y - 4]²
[y - 4]² = 144
y - 4 = ± 12
y = 16, -8
Thus, the required value of y for the given segment AB is given as y = 16, -8.
Learn more about lines here:
brainly.com/question/2696693
#SPJ1
Please look at photo. Thank you!
Polynomial and rational functions:
A) Find all x and y intercepts. Check all that apply:
X intercepts: 4, 0, 1, and/or none.
Y intercepts: 1, 4, 0 and/or none.
B) write the equations for all vertical and horizontal asymptotes. Enter the equations by writing “and” or “none” when necessary.
C) find the domain and range of f. Write each answer as an interval or union of intervals.

Answers
A) All x- and y-intercepts include the following:
x-intercepts: none.
y-intercept: 1.
B) The equation for vertical asymptote is x = 4 and the equation for horizontal asymptote is y = 0.
C) The domain and range of f are:
Domain = [-∞, 4) U [4, ∞]
Range = [0, ∞]
What is the x-intercept?In Mathematics, the x-intercept is the point at which the graph of a function crosses or touches the x-coordinate and the y-value or value of "y" is equal to zero (0).
Part A.
Based on the graph of this rational function, the x-intercept and y-intercept include the following:
x-intercept: none.
y-intercept: 1.
Part B.
An equation that represents the vertical asymptote is x = 4 while the equation represents the horizontal asymptote is y = 0 because the line does not cross those points.
Part C.
By critically observing the graph of this rational function, we can logically deduce the following domain and range:
Domain = [-∞, 4) U [4, ∞] or {x|x ≠ 4}.
Range = [0, ∞] or {y|y ≥ 0}.
Read more on horizontal asymptote here: brainly.com/question/25566825
#SPJ1
A carpenter is building four picture frames in the shape of right triangles. He calculates the lengths of the longest side of each triangle, in inches. Which list of lengths is in order from shortest to longest?
Answers
Answer:
Step-by-step explanation:
This problem requires the use of the Pythagorean Theorem to find the lengths of the sides of a piece of property in the shape of a right triangle
Example:
Taylor finds a piece of property in the shape of a right triangle. She finds that the longer leg is 10 m shorter than twice the length of the shorter leg and the hypotenuse is 20 m longer than the longer leg. Find the lengths of the sides of the triangular lot.
What is the slope of the line through (- 1, - 7) and (3, 9) ?
Choose 1 answer:
A - 1/4
B
- 4
C 4
D 1/4
Answers
Answer:
C. 4
Step-by-step explanation:
Use the slope formula:
\(m=\frac{y2}{x2} -\frac{y1}{x1}\)
m = the slope.
Substitute the values into the formula:
\(\frac{9}{3} -\frac{-7}{-1} =\frac{?}{?}\)
Solve:
\(\frac{9}{3} -\frac{-7}{-1} =\frac{16}{4}\)
Simplify 16/4:
\(\frac{16/4}{4/4} =\frac{4}{1}=4\)
Help I need answers now

Answers
Answer:
The Answer in Exact Form:
-3/22
In Decimal Form:
-0.136
Step-by-step explanation:
-\(\frac{3}{2}\)÷5\(\frac{1}{2}\)=-3/22
Lie detectors are controversial instruments, barred from use as evidence in many courts. Nonetheless, many employers use lie detector screening as part of the hiring process in the hope that they can avoid hiring people who might be dishonest. There has been some research, but no agreement, about reliability of polygraph tests. Based on the research, suppose a polygraph can detect 65% of lies, but incorrectly identifies 15% of true statements as lies.
A certain company believes 95% of job applicants are trustworthy. The company gives everyone a polygraph test asking, "Have you ever stolen anything from your work place?" Naturally, all applicants answer "No", but the polygraph identifies some of the answers as lies, making the person ineligible for a job. What is the probability that a job applicant rejected under suspicion of dishonesty was actually trustworthy?A) 0.143
B) 0.618
C) 0.333
D) 0.814
Answers
the probability that a job applicant rejected under suspicion of dishonesty was actually trustworthy is 0.814
What is mean by probability?Probability is a measure of the likelihood of a particular event occurring, expressed as a number between 0 and 1. It is a mathematical tool used to quantify the likelihood of an event occurring, or the likelihood of a proposition being true.
Step 1: Calculate the probability that an applicant is trustworthy:
P(trustworthy) = 95% = 0.95
Step 2: Calculate the probability that an applicant is untrustworthy:
P(untrustworthy) = 100% - 95% = 5% = 0.05
Step 3: Calculate the probability that the lie detector correctly identifies a trustworthy applicant as trustworthy:
P(trustworthy applicant correctly identified) = 65% = 0.65
Step 4: Calculate the probability that the lie detector incorrectly identifies a trustworthy applicant as untrustworthy:
P(trustworthy applicant incorrectly identified) = 15% = 0.15
Step 5: Calculate the probability that a job applicant rejected under suspicion of dishonesty was actually trustworthy:
P(job applicant rejected under suspicion of dishonesty was actually trustworthy) = P(trustworthy applicant correctly identified) x P(trustworthy) + P(trustworthy applicant incorrectly identified) x P(trustworthy)
= 0.65 x 0.95 + 0.15 x 0.95
= 0.814
To learn more about probability refer to:
https://brainly.com/question/24756209
#SPJ1
x less than the quantity y divided by 9 is more than 21.
What is a way to write this sentence as an algebraic inequality?

Answers
Answer:
It's C.
Step-by-step explanation:
Did the test
The inequality is y/9 - x > 21.
What is Inequality?Mathematical expressions with inequalities are those in which the two sides are not equal. Contrary to equations, we compare two values in inequality. Less than (or less than or equal to), greater than (or greater than or equal to), or not equal to signs are used in place of the equal sign.
Given:
x less than the quantity y divided by 9 is more than 21.
Now, writing the mathematical Inequality for the given statement is
x less than the quantity y divided by 9
y/9 -x
and, more than 21.
y/9 - x > 21
Hence, the inequality is y/9 - x > 21.
Learn more about Inequality here:
https://brainly.com/question/30231190
#SPJ2
A nine-month old baby drank an average of 7 1/4 oz during each of four feedings. If the baby drank 7 1/2oz, 7 3/8oz, & 6 3/8oz in the first three feedings, how many ounces were taken during the fourth feeding?
A) 7 3/8
B) 6 3/8
C) 6 3/4
D) 7 3/4
Show work please
Answers
Answer: D) 7 3/4
Step-by-step explanation:
With averages, we add all the values and divide by the number of values. Here, we know three out of the four days, let's label the day we don't know x. There are four days, so we can divide by four. 7 1/4 is the average, so we can set the equation equal to 7 1/4.
7 1/4 = (7 1/2 + 7 3/8 + 6 3/8 + x) / 4
Let's multiply both sides by 4 to get rid of the fraction. Let's also add what is in the parentheses
29 = 21 1/4 + x
Now we can isolate x by subtracting 29-21 1/4
so
x = 7 3/4 thus the answer is D
Answer:
D) 7 3/4
Step-by-step explanation:
Let x = amount of last feeding.
7 1/4 = (7 1/2 + 7 3/8 + 6 3/8 + x)/4
4 × 7 1/4 = 7 1/2 + 7 3/8 + 6 3/8 + x
28 + 1 = 7 4/8 + 7 3/8 + 6 3/8 + x
29 = 20 10/8 + x
(20 10/8 is the same as 20 + 10/8 = 20 + 8/8 + 2/8 = 20 + 1 + 1/4 = 21 + 1/4 = 21 1/4)
29 = 21 2/8 + x
29 = 21 1/4 + x
x = 29 - 21 1/4
x = 28 4/4 - 21 1/4
x = 7 3/4
Answer: 7 3/4
The percentage of total variation in the dependent variable that is described by the independent variable is expressed by_________.
a. coefficient of determination
b. correlation coefficient
c. coefficient of covariation
d. regression coefficient
a. coefficient of determination
Answers
The percentage of total variation in the dependent variable that is described by the independent variable is expressed by coefficient of determination . So, correct answer is option (a).
The coefficient of determination R² is equal to the square of the correlation coefficient, r² expressed as a percentage, represents the percentage of variation in the dependent variable y that can be explained by variation in the independent variable x using the regression line. Coefficient of determination is a statistical measure that examines how differences in one variable can be explained by differences in her second variable. In other words, this coefficient, commonly known as R-squared (or R²), measures how strong the linear relationship between two variables is. This coefficient is commonly known as the R-square (or R²) and is sometimes called the "goodness of fit". This measurement is expressed as a value between 0.0 and 1.0..
To learn more about Cofficient of determination, refer:
https://brainly.com/question/17237825
#SPJ4
Which two ratios represent quantities that are proportional?
20
24
10
O A. and
O B. and
O c. and 1
O D. 1 and 14

Answers
Answer:
c. 1 and 14
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
i did the quiz
Determine which integers in the set S: {−2, −3, −4, −5} will make the inequality 4p − 7 ≥ 9p + 8 true.
PLS HELP ME
Answers
The integers in the set s: {-2,-3,-4,-5} will make the inequality 4p-7 \(\geq\) 9p+8 true are : -3, -4, -5
Let's solve the inequality first
4p -7 \(\geq\) 9p +8
Taking p's on the same side we will get :
-7 - 8 \(\geq\) 9p - 4p
-15 \(\geq\) 5p
Divide by 5 into both sides
-3 \(\geq\) p
i.e. p \(\leq\) -3
Therefore p must be less than or equal to -3
From the set, we have the numbers -3,-4,-5 which are less than or equal to -3
Hence the integers -3,-4,-5 will make the inequality 4p-7 \(\geq\) 9p+8 true
To learn more about inequality:
https://brainly.com/question/30238989
The perimeter of a rectangle is 245 feet. The short sides are each 30 feet long, but the lengths of the long sides are unknown. What equation represents this situation?
Answers
Answer:
2(30) + 2x = 245
Step-by-step explanation:
As u know a rectangle has four sides, two equally long sides and two equally short sides. If each of the short sides are 30, that means 30 times 2 adding the 2 missing long sides would equal 245. So the long sides are going to be represented with x in this equation:
2(30) + 2x = 245
To make sure our equation is right, lets try solving it:
2(30) + 2x = 245
60 + 2x = 245
subtract 60 from both sides
2x = 185
x = 92.5
Now put 92.5 in the equation instead of x to confirm:
2(30) + 2(92.5) = 245
60 + 185 = 245
245 = 245
what is the value of x

Answers
\(\text{In}~ \triangle ABC,\\\\~~~~~~~~\sin 45^{\circ} =\dfrac{BC}{AC} \\\\\implies \dfrac 1{\sqrt 2} = \dfrac{BC}{6\sqrt 2}\\\\\\ \implies BC= 6\\\\\text{Now, In}~ \triangle BCD\\\\~~~~~~\cos 60^{\circ} = \dfrac{BD}{BC}\\\\\ \implies \dfrac 12 = \dfrac{x}{6}\\\\\\\implies x = \dfrac 62\\\\\\\implies x = 3\)
Answer:
x = 3
Step-by-step explanation:
using the sine ratio in right triangle ABC and the exact value
sin45° = \(\frac{1}{\sqrt{2} }\) , then
sin45° = \(\frac{opposite}{hypotenuse}\) = \(\frac{BC}{AC}\) = \(\frac{BC}{6\sqrt{2} }\) = \(\frac{1}{\sqrt{2} }\) ( cross- multiply )
BC × \(\sqrt{2}\) = 6\(\sqrt{2}\) ( divide both sides by \(\sqrt{2}\) )
BC = 6
using the cosine ratio in right triangle BCD and the exact value
cos60° = \(\frac{1}{2}\) , then
cos60° = \(\frac{adjacent}{hypotenuse}\) = \(\frac{BD}{BC}\) = \(\frac{x}{6}\) = \(\frac{1}{2}\) ( cross- multiply )
2x = 6 ( divide both sides by 2 )
x = 3
A pack of gum costs $1.00. There are 10 sticks of gum in a pack. The unit rate is____ cents.
Answers
Answer:
the unit rate is 10 cents
Step-by-step explanation:
divide $1.00 and 10 which is $0.10 or 0.1
Help please will mark brainliest!!!

Answers
Answer:
18
Step-by-step explanation:
BRAINLIEST TO CORRECT ANSWER!
The amount of energy taken in by a plant in the form of solar radiant energy, should be equal to the sum of the amount of energy that the plant uses in life processes such as growing and respiration.
Group of answer choices
True
False
Answers
Answer:
True
Step-by-step explanation:
In order to grow, a plant needs all the radient energy that it can get.
make e the subject
e-5=2f
Answers
Answer:
e-5=2f
take '-5' to the other side where '2f' is
e=2f+5
Can someone pls help me with this
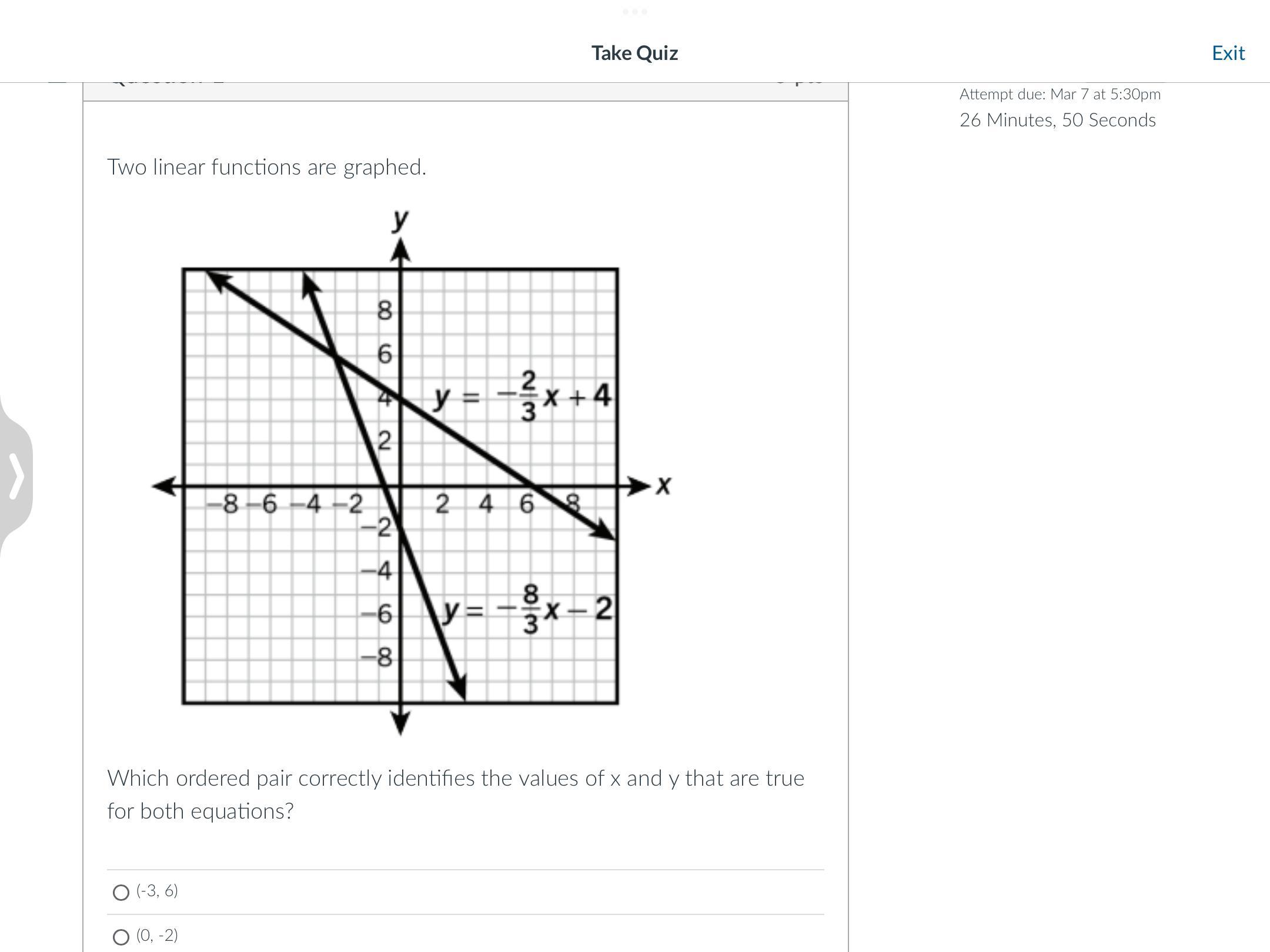
Answers
Answer: The first one (-3,6)
Step-by-step explanation:
Both linear functions meet at (-3,6).
You can graph both linear functions on the Desmos graphing calculator website to verify your answer.
A pebble dropped from a bridge strikes the water in exactly 9.5 seconds. How high is the bridge?
Answers
The height of the bridge is 442.23m.
In the question ,
it is given that
time taken(t) to reach the pebble from bridge to the water = 9.5 sec
the initial velocity(u) = 0 ....as the ball was at rest ,
the acceleration(a) is the gravity = 9.8 m/s
let s be the distance between bridge and water , which means the height of the bridge = h
Now by the second equation of motion , we have
h = u*t + (1/2)*a*t²
Substituting the values of u, a, t from above , we get
h = 0*9.5 + (1/2)*9.8*(9.5)²
h = 0 + (1/2)*9.8*90.25
h = 0 + 884.45/2
h = 884.45/2
h = 442.225
h ≅ 442.23
Therefore , if a pebble dropped from a bridge strikes the water exactly 9.5 sec then the height of the bridge is 442.23m .
Learn more about Distance here
https://brainly.com/question/559832
#SPJ1
The average number of points a basketball team scored for three games was 63 points. They scored the same number of points, which was 6 points more than they scored in the third game
Answers
a class has 28 students 13 boys and 15 girls what is rstio girls to boys
Answers
Answer:
15 : 13
Step-by-step explanation:
Girls : Boys
15 : 13
If
f(x) = 2x² + 3x - 6, determine the value of f(2).
Answers
Answer:
8
Step-by-step explanation:
2x² + 3x - 6
plug in x with 2
2(2)^2+3(2)-6
2(4)+6-6
8+6-6
14-6
8
A virus takes 5 days to grow from 90 to 200. How many days will it take to grow from 90 to 410? Round to the nearest whole number.
Answers
The number of days it will take the virus to grow from 90 to 410 is 15 days.
What is the growth rate of the virus?The growth rate of the virus is calculated as follows;
growth rate = (200 - 90) / 5
growth rate = 22 per day
The number of days it will take the virus to grow from 90 to 410 is calculated as follows;
growth = 410 - 90
growth = 320
Number of days = 320 / 22/day = 14.55 ≈ 15 days
Learn more about growth rate here: https://brainly.com/question/25849702
#SPJ1
What is 858 divided by 57 show your work
Answers
Answer: 286/19, 15.052632 and 1
15
19
Calculate; 858/57
You can see the division procedure, below.
\(\bf{\red{ \ \ \ \ \ 1 \ 5 }} \\ \bf{57 \ |\overline{8 \ 5 \ 8}}\\ \bf{ \ \ \underline{ - \ 5 \ 7}}\\ \bf{ \ \ \ \ \ 2 \ 8 \ 8}\\ \bf{ \ \ \underline{- \ 2 \ 8 \ 5}}\\ \bf{\ \ \ \ \ \ \ \ \ \ \ 3}\)
Good luck.Solve....3(x+3)=-4x+30
Answers
Answer:
x=3
Step-by-step explanation:
Hey there!
In order to solve this equation, we must first distribute the 3
3x + 9 = -4x + 30
Now we combine like terms
7x = 21
Then we divide both sides by 7 to get x by itself
x = 21/7
x = 3
Answer: x=3
Step-by-step explanation:
To solve the given equation, it means to find the value of x. We want to use inverse properties to isolate x. The inverse properties are add/subtract and multiply/divide. Be sure to use the corresponding inverse operation.
3(x+3)=-4x+30 [distribute]
3x+9=-4x+30 [add both sides by 4x]
7x+9=30 [subtract both sides by 9]
7x=21 [divide both sides by 7]
x=3
Therefore, we get x=3.
find the volume V of the solid generated by revolving the region bounded by the given lines and curves about x axis for y = x^2, y =0, x =2.
Answers
The volume of the solid generated is V=8π and 32/5π
Given functions are x=y², x=2 and y=0
The equation y=x² is a parabola opening to right and has a vertex at O(0,0)
and another y=0 is the x-axis and x=2 is a line parallel to the y-axis
The region bounded by the above will be formed once their intersection points are known.
y²=2⟹y=±√2
OFB is bounded by O(0,0), F(2,0) and B(2,√2)
Let V be the volume of solid generated when the region OFB is revolved around line x=2.
\(V=\pi \int\limits^2_0 {x^4} \, dx \\\)
V=π[x⁵/5]²₀
V=π[(2)⁵/5]
V=32/5 π.
\(V=\pi \int\limits^4_0 {(2^2)_2-(\sqrt{y}^2)_3 } \, dy\\\\ V=\int\limits^4_0 {(4-y)} \, dx\)
V=8π.
when the shaded region revolves the bout x-axis:
\(V=\pi \int\limits^b_a {y^2} \, dx \\\\V=\pi \int\limits^2_0 {y^2} \, dx =\pi \int\limits^2_0 {x^4} \, dx =\pi [\frac{1}{5}.x^5]_0^2\\\\ V=\pi [\frac{32}{5}-0]\)
V=32/5
when the shaded region revolves the bout y-axis:
\(V=\pi \int\limits^c_d [(x^2)_2-(x^2)_1} \, dx \\V=\pi \int\limits^4_0 [(2^2)_2-(\sqrt{y} ^2)_1} \, dy \\V=\pi \int\limits^4_0 {(4-y)} \, dy =\pi [4y-\frac{1}{2}y^2]_0^4\)
V=π[16-8]
V=8π
To know more about the Volume of a solid:
https://brainly.com/question/16717260
#SPJ4