Write an equation in standard form for the line that has an undefined slope and passes through (–6, 4).
Answers
Answer:
Step-by-step explanation:
so if has an undefined slope it would have to be x= something
the equation that works here is x=-6
Related Questions
if carpet cost s $1.50 per square foot including the cost of installation how much would it cost to carpet the entire living room floor of the cabin shown at the right?
Answers
The amount of cost to carpet the entire rectangular living room floor of the cabin is given by A = $ 420
What is the Area of a Rectangle?The area of the rectangle is given by the product of the length of the rectangle and the width of the rectangle
Area of Rectangle = Length x Width
Given data ,
Let the area of the rectangular living room be A
The scale factor is 1 cm of graph = 4 feet
Now , the length of rectangular floor be L = 5 cm
So , the length of the rectangular floor L = 20 feet
And , the width of the rectangular floor W = 3.5 cm
So , the width of the rectangular floor W = 14 feet
The cost per unit area of carpet = $ 1.50
The area of rectangular floor = L x W
On simplifying , we get
The area of rectangular floor = 20 x 14 = 280 feet²
Now , the cost to carpet 280 feet² of living room = 280 x cost per unit area of carpet
The amount of cost to carpet the entire living room floor = 280 x 1.5
The amount of cost to carpet the entire living room floor = $ 420
Hence , the cost to carpet the living room is $ 420
To learn more about area of rectangle click :
https://brainly.com/question/15225905
#SPJ7
The complete question is :
If carpet cost s $1.50 per square foot including the cost of installation how much would it cost to carpet the entire living room floor of the cabin shown at the right?

lect the correct answer.
Under which condition is the sample proportion, , a point estimate of the population proportion?
A.
The sample proportion is never a point estimate of the population proportion.
B.
The sample represents a proportion of the population.
C.
The sample proportion is unbiased.
D.
The sample size, n, is small enough.
Reset Next
Answers
The correct answer is B. The sample represents a proportion of the population.
What is the sample population ?
A point estimate is a single value used to estimate a population's unknown parameter. The sample proportion (denoted by p), in the context of determining the population proportion, is a widely used point estimate. The sample proportion is determined by dividing the sample's success rate by the sample size.
The sample must be representative of the population for it to be a reliable point estimate of the population proportion. To accurately reflect the proportions of various groups or categories present in the population, the sample should be chosen at random.
Learn more about population:https://brainly.com/question/30324262
#SPJ1
Tomas combined 7.28 ounces of strawberries with 8.06 ounces of blueberries to make fruit bowls. He pours the fruit equally into four bowls and has a 1.58 ounces of fruit left over. How many ounces of fruit
Answers
Given :
Tomas combined 7.28 ounces of strawberries with 8.06 ounces of blueberries to make fruit bowls.
He pours the fruit equally into four bowls and has a 1.58 ounces of fruit left over.
To Find :
Weight of each ounces of fruit bowl.
Solution :
Sum of fruits , S = 7.28 + 8.06 = 15.34 ounces.
Weight of put he filled in 4 bowls, W = 15.34 - 1.58 = 13.76 ounces.
So, weight of each fruit bowl is :
\(w=\dfrac{13.76}{4}\\\\w=3.44\ pounds\)
Hence, this is the required solution.
Use geometry to evaluate

Answers
Refer to the images attached. Now I am guessing when it says "use geometry" was to graph it? I wasn't completely sure. I attached how I would normally evaluate that problem and a graph of the piecewise function. It has been a while since I have dealt with integrating piecewise function, please let me know what process you were supposed to use if you figure it out. Hope this helps you a bit, have a good one!


How do i solve this question?

Answers
1. Volume of Water= 35.25 unit³
2. Volume of 1 ice = 1.4 unit³
3. Volume of 3 ice cubes submerged = 3.78 unit³
1. Volume of Water
= πR²H
= 3.14 x 3/2 x 3/2 x 5
= 3.14 x 45/4
= 35.25 unit³
2. Volume of 1 ice
= π(r2² - r1²)h
= 3.14 x [(4/6)² - (2/6)²] x 4/3
= 3.14 x 12/36 x 4/3
= 3.14 x 1/3 x 4/3
= 1.395
= 1.4 unit³
3. Volume of 3 ice cubes submerged
= 3 x (9/10 x 1.4)
= 3.78 unit³
4 . Total Height displacement
= 5 - 4/3
= 11/3 unit
Learn more about Volume here:
https://brainly.com/question/28058531
#SPJ1
This is a multiple step question

Answers
Answer:
Step-by-step explanation:
In this type of question , if the difference b/w the numerator and the denominator is 1 , then simply check the numerator . Whichever is big , it will be the larger .
In this question ,
\(\frac{8}{9} \\\frac{7}{8} \\\\\)
here , we can see that 9 - 8 = 1 & 8 - 7 = 1
∵ 8 > 7
∴ \(\frac{8}{9} > \frac{7}{8}\)
For common denominator , find its LCM : LCM(8,9) = 72
∴ Common denominator is 72 .
P= 9000, r= 2.0%, t= 15 months. Find the simple interest owed for the use of the money. Assume there are 360 days in a year
Answers
Answer:
Step-by-step explanation:
S.I= PTR/100
=9000*(15/12)*2/100
=90*5/2
=450/2
=225
Find the slope and the -intercept of the line -8x-4y=-5
Answers
Answer:
The slope is -2 and y-intercept is (0, 5/4).
Step-by-step explanation:
-8x-4y=-5
4y=-8x-(-5)
4y=-8x+5
y=-8/4x+5/4
y=-2x+5/4
y=mx+b where m=slope and b=y-intercept.
Thus, m=-2 and b=5/4.
The difference between x and 2 is less than 9
Answers
Answer:
difference between x and 2
Step-by-step explanation:
x-2< 9
x< 11
Pls help only one question :( im stuck!

Answers
Answer:
-√26, 5.15, 5.2, 16/3
Step-by-step explanation:
-√26 = -5.09
16/3 = 5.33
M = I1+I₂ 31 +32 2 Now let's substitute in our given values. (-2 , 2) = ((-5 Find 2 and y2 We will now set up two equations to solve for our two unknowns of x2 and y₂. (-5 X2 (-5+₂) -5+22), (7+)) 2 - +₂)/2 = We will first want to multiply by 2 on both sides and will get −5+₂= -4 Adding 5 to both sides we get = 7 This is the coordinate of point B. Now we will set up the equation to solve for y2 +y2)/2 =
Answers
The coordinates of point B are (-3, 17).
The given equation is M = I₁ + I₂ = 31 + 32.
Now let's substitute in our given values:
(-2, 2) = ((-5 + x₂) / 2, (-5 + 2 + y₂) / 2)
We will now set up two equations to solve for our two unknowns, x₂ and y₂:
Equation 1: (-5 + x₂) / 2 = -4
Multiply both sides by 2:
-5 + x₂ = -8
Add 5 to both sides:
x₂ = -3
This gives us the x-coordinate of point B.
Equation 2: (-5 + 2 + y₂) / 2 = 7
Simplify:
(-3 + y₂) / 2 = 7
Multiply both sides by 2:
-3 + y₂ = 14
Add 3 to both sides:
y₂ = 17
This gives us the y-coordinate of point B.
Therefore, the coordinates of point B are (-3, 17).
For more such questions on coordinates
https://brainly.com/question/29660530
#SPJ8
An office manager orders one calculator or one calendar for each of the office's 60 employees. Each calculator costs $15, and each calendar costs $10. The entire order totaled $800.
Part A: Write the system of equations that models this scenario. (5 points)
Part B: Use substitution method or elimination method to determine the number of calculators and calendars ordered. Show all necessary steps. (5 points)
Answers
The system of equations is.
\(\begin{cases}\text{x}+\text{y}=60 \\15\text{x}+10\text{y}=800 \end{cases}\)
And the solutions are y = 50 and x = 10.
How to write and solve the system of equations?Let's define the two variables:
x = number of calculators.y = number of calendars.With the given information we can write two equations, then the system will be:
\(\begin{cases}\text{x}+\text{y}=60 \\15\text{x}+10\text{y}=800 \end{cases}\)
Now let's solve it.
We can isolate x on the first to get:
\(\text{x} = 60 - \text{y}\)
Replace that in the other equation to get:
\(15\times(60 - \text{y}) + 10\text{y} = 800\)
\(-2\bold{y} = 900 - 800\)
\(-2\bold{y} = 100\)
\(\text{y} = \dfrac{100}{-2} = \bold{50}\)
Then \(\bold{x=10}\).
Therefore, the solutions are y = 50 and x = 10.
Learn more about systems of equations at:
https://brainly.com/question/31812807
Find the slope (2,5) (9,3)
Answers
Answer:
-0.2857
Step-by-step explanation:
\(\frac{3-5}{9-2}\)
= -2/7
= -0.2857
Answer:
the slope is 1/2
Step-by-step explanation:
the formula you use for this is (x1 - y1)/(x2 - y2) then after subtracting you will have a fraction and you will have to simplify, so (2-5)/(9-3) + -3/6, then you simplify that to 1/2 and that should give you your answer!
what is ( 5 x 1 ) + ( 5 x 1/3)
Answers
Answer:
The answer is 20/3
Step-by-step explanation:
(5 x 1 ) + ( 5 x 1/3)
5 + ( 5 × 1/3 )
5 + 5/3 = 20/3
4. The two legs of a right triangle are equal and the square of its hypotenuse is 50. Find the
length of each leg.
Answers
Answer:
\(Opposite = Adjacent= 5\)
Step-by-step explanation:
Given
\(Hypotenuse^2 = 50\)
\(Opposite = Adjacent\)
Required
Find the length of each leg
This is calculated using Pythagoras Theorem
\(Opposite^2 + Adjacent^2 = Hypotenuse^2\)
\(Opposite^2 + Adjacent^2 = 50\)
Represent the opposite and adjacent with x
\(x^2 + x^2= 50\)
\(2x^2 = 50\)
Divide both sides by 2
\(x^2 = 25\)
Take square roots
\(x = 5\)
Hence:
\(Opposite = Adjacent= 5\)
Given the figure below, find the values of x and z.
108
(12x+24)

Answers
We know that two vertical angles are equal.
\(108° \: = \: (12x \: + \: 24)°\)
\( - 12x \: = \: 24 \: - \: 108\)
\( - 12x \: = \: -84\)
\( \boxed{ \bold{x \: = \: 7°}}\)
We calculate "x":We know that a complete angle measures 360°.
\(108° \: + \: 108° \: + \: z \: + \: z \: = \: 360°\)
\(216 \: + \: 2z \: = \: 360\)
\(2z \: = \: 360 \: - \: 216\)
\(2z \: = \: 144\)
\( \boxed{ \bold{z \: = \: 72°}}\)
Answer: x = 7 z = 72 °the scale drawing of a rectangular room measures 10 cm long by 6 cm wide. the actual width of the room is 15 feet. what is the actual perimeter of the room, in feet?
Answers
Answer:
80 feet
Step-by-step explanation:
6 cm = 15 feet
1 cm = 5/2 feet
32 cm = 90 feet
The actual perimeter of the room is 90 feet.
What is a scale factor?A scale factor is defined as the ratio between the scale of a given original object and a new object,
We have,
The scale drawing of a rectangular room measures 10 cm long by 6 cm wide.
The actual width of the room is 15 feet.
This means,
6cm = 15 feet
1 cm = 15/6 feet
1 cm = 5/2 feet
Now,
The perimeter of the rectangular room.
= 2(10 + 6)
= 2 x 16
= 32 cm
1 cm = 5/2 feet
So,
32 cm = 32 x 5/2 feet
32 cm = 16 x 5 feet
32 cm = 90 feet
Thus,
The actual perimeter of the room is 90 feet.
Learn more about scale factors here:
https://brainly.com/question/20759556
#SPJ2
max is using a hose to fill an above ground swimming pool, which is shaped like a rectangular prism. the pool is 7meters long and 3 meters wide, and max plans to fill the pool with water 0.75 meters deep. the house flows at a rate of 2,250 liters, or 2.25 cubic meters, per hour.
how long does it take to fill the pool?
write your answer as a whole number or decimal. do not round.
Answers
Using the volume of the rectangular prism, it is found that it takes 7 hours to fill the pool.
What is the volume of a rectangular prism?The volume of a rectangular prism of dimensions l, w and h is given by the multiplication of it's dimensions, that is:
V = lwh.
In this problem, the dimensions in meters are: l = 7, w = 3, h = 0.75. Hence, the volume in cubic meters is:
V = lwh = 7(3)(0.75) = 15.75.
It fill 2.25 cubic meters per hour, hence, for 15.75 cubic meters, the time taken is:
15.75/2.25 = 7 hours.
More can be learned about volume of a rectangular prism at https://brainly.com/question/17223528
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
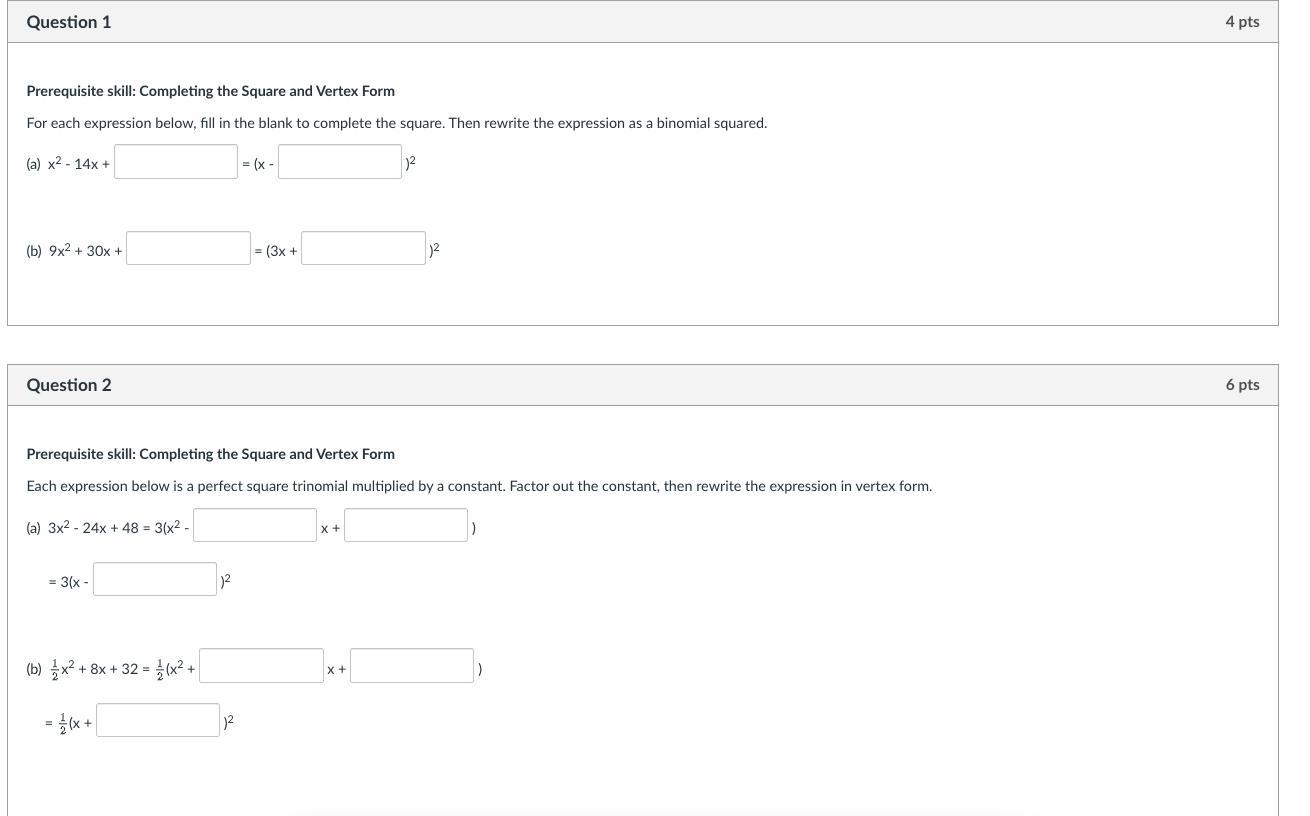
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
Which of the following is equivalent to the radical expression below when X>7? √x-7•√x+1 OA. √x²+8x-7 OB. √x²-6x+7 OC. square root x^2+8x+7OD. square root x²-6x-7

Answers
Given:
The given radical expression is,
\(\sqrt{x-7}\cdot\sqrt{x+1}\)Required:
To find the expression equivalent to the given radical expression when
\(x>7\)Explanation:
Let us solve the given expression.
\(\begin{gathered} \sqrt{x-7}\cdot\sqrt{x+1} \\ =\sqrt{(x-7)\cdot(x+1)} \\ =\sqrt{x^2+x-7x-7} \\ =\sqrt{x^2-6x-7} \end{gathered}\)Final Answer:
The expression equivalent to the given radical expression when
\(x>7\)is given by,
\(\sqrt{x^2-6x-7}\)Option D is correct.
In ΔWXY, w = 320 inches, y = 740 inches and ∠Y=169°. Find all possible values of ∠W, to the nearest 10th of a degree.
Answers
$dfrac{sinangle W}{320}=dfrac{sin169°}{740}$
Multiplying both sides by 320, we have:
$sinangle W=dfrac{320sin169°}{740}$
Using a calculator, we find that $sinangle W approx 0.7555$. Taking the inverse sine of both sides, we have:
$angle W approx sin^{-1}(0.7555)$
There are two possible values for $angle W$: $angle W approx 49.5°$ and $angle W approx 130.5°$ (since $sin^{-1}(0.7555) approx 49.5°$ and $angle W = 180° - sin^{-1}(0.7555) approx 130.5°$).
Therefore, the two possible values of $angle W$ are approximately 49.5° and 130.5°.
what is the largest number that can divide 35,50 and 40 exactly?
Answers
the answer is 5 cuz the gcf of the given numbers is 5
A right circular cone has a height of 10 centimeters and a base of 9cm. What is the volume of the cone
Answers
Answer:
19cm
Step-by-step explanation:
The volume of the give cone is 21.40 cm³
What is a cone?A cone is a shape formed by using a set of line segments or the lines which connects a common point, called the apex or vertex, to all the points of a circular base(which does not contain the apex). The distance from the vertex of the cone to the base is the height of the cone.
Given that, A right circular cone has a height of 10 centimetres and a base of 9 cm.
The circumference of the base is 9 cm
Therefore, 2πr = 9
r = 9/3.14×2
r = 1.43 cm
Volume of a cone = πr²h/3
V = 3.14(1.43)²10/3
V = 21.40 cm³
Hence, The volume of the give cone is 21.40 cm³
For more references on cones, click;
https://brainly.com/question/16394302
#SPJ2
help please!! 10 points!

Answers
log x/ y^9
log x - log y^9
log x - 9log y
If you want me to explain the rules I’m using more in depth lmk!
Tyler is 6 feet tall and Blake measures his shadow to be 10 ½ feet long. Maddie measures the shadow of the tree to be 21 feet long. How tall is the tree to the nearest tenth of a foot.
20 Points

Answers
The tree is approximately 12 feet tall to the nearest tenth of a foot.
We have,
To find the height of the tree, we can set up a proportion using the measurements of the shadow.
Since we know that Tyler is 6 feet tall and his shadow is 10 ½ feet long, we can set up the following expression:
Tyler's height / Tyler's shadow length = Tree's height / Tree's shadow length
6 feet / 10.5 feet = Tree's height / 21 feet
To find the tree's height, we can cross-multiply and solve for it:
6 feet x 21 feet = 10.5 feet x Tree's height
126 feet = 10.5 feet x Tree's height
Dividing both sides of the expression by 10.5 feet:
126 feet / 10.5 feet = Tree's height
12 feet = Tree's height
Therefore,
The tree is approximately 12 feet tall to the nearest tenth of a foot.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
Select the correct answer.
Which investment data is best modeled by an exponential function?
A.
The chart shows the Growth of dollars 1,000 in years on the x-axis and on the y-axis is the account balance. The account balance was 1000 dollars on year 1 and with a linear growth reached 2900 dollars at the end of 18 years.
B.
The chart shows the Growth of dollars 1,000 in years on the x-axis and on the y-axis is the account balance. The account balance was 1000 dollars in year 1. It reached 4000 dollars after 11 years and at the end of 18 years, it falls to 1000 dollars.
C.
The chart shows the Growth of dollars 1,000 in years on the x-axis and on the y-axis is the account balance. The account balance was 1000 dollars on year 1 and at the end of 18 years, it was 58,000 dollars.
D.
The chart shows the Growth of dollars 1,000 in years on the x-axis and on the y-axis is the account balance. The account balance remained stable at 1000 dollars for 15 years, and then increased to 1400 dollars after 18 years.
E.
The graph depicts the Growth of dollar 1,000 with the x-axis representing time in years and the y-axis representing account balance. The account balance was 1000 dollars in the first year. It reached the peak of 1800 dollars in year 14.
Answers
Answer:
Letter (C)
Step-by-step explanation:
The chart shows the Growth of dollars 1,000 in years on the x-axis and on the y-axis is the account balance. The account balance was 1000 dollars on year 1 and at the end of 18 years, it was 58,000 dollars. This type of data is best modeled by an exponential function because it shows a continuous increase in the account balance over time.
Evaluate the expression when y = 4. 5 + y + 8
Answers
Answer: 17
Step-by-step explanation:
Answer:
12.5
Step-by-step explanation:
To evaluate an algebraic expression, you have to substitute a number for each variable ( y for 4.5 as in the question ) and perform the arithmetic operations ( then add 4.5 + 8 )
4.5 + 8 = 12.5
HOPE THIS HELPED
what is the value of x?
help would be so appreciated!

Answers
Answer:
x =23
Step-by-step explanation:
ok first, the full degree of a straight line is 180°
subtract 38° out of 180°
180-38= 142
so 6x+4= 142°
subtract 4 from both sides of the equation
6x +4 -4= 142-4
6x=138
divide 6 from 6x and 138
x=23
Determine whether the given value is a solution of the equation. Show your work.
21 = x − 5; x = 16
Answers
Step-by-step explanation:
No Not an answer
21=x-5
x=26
A travel agent makes the hypothesis:
More holiday refunds are given in the winter than in the summer.
a) Use the information in the bar chart to work out:
- i) the mean number of refunds given in the summer.
- ii) the mean number of refunds given in the winter.
b) Does your answer to part a) support the hypothesis or not?

Answers
a)
i) The mean number of refunds given in the summer is 21.
ii) The mean number of refunds given in the winter is 20.
b) The answer to part a) does NOT support the hypothesis.
How is this so?To calculate the mean number of refunds given in the summer and winter,we need to find the average of the values for each season over the given years. Let's calculate -
a) Mean number of refunds given in the summer -
(20 + 15 + 10 + 15 + 32 + 34) / 6
= 126 / 6
= 21
b) Mean number of refunds given in the winter -
(24 + 10 + 15 + 18 + 26 + 27) / 6
= 120 / 6
= 20
The mean number of refunds given in thesummer is 21, and the mean number of refunds given in the winter is 20.
b) Based on the calculated means, the answer to part a) does NOT support the hypothesis.
The mean number of refunds given in the summer (21) is greater than the mean number of refunds given in thewinter (20), indicating that more refunds are given in the summer than in the winter, contrary to the hypothesis.
Learn more about hypothesis at:
https://brainly.com/question/606806
#SPJ1