Which situation is best modeled with a division expression?
finding the number of equal-sized parts into which a number can be split
finding the combined value of several different numbers
finding the distance between two numbers on a number line
finding the total value when several of the same number are grouped together
Answers
Answer: Finding the number of equal-sized parts into which a number can be split
Step-by-step explanation:
Hi, a division expression is the division of 2 numbers that results in a quotient.
The quotient is the number of times that the second number in the division is contained in the first number.
For example 20 ÷ 2 = 10
Number 2 is contained 10 times in the number 10, or in other words, 20 can be split into ten equal-sized parts.
Feel free to ask for more if needed or if you did not understand something.
Answer:
A
Step-by-step explanation:
for edge
Related Questions
A study on students drinking habits wants to determine the true average number of alcoholic drinks all uf greek students have in a one week period. We know from preliminary studies that the standard deviation is around 6. 3. How many students should be sampled to be within 0. 5 drink of population mean with 95% probability?.
Answers
Number of students need to be sampled = 610
A study to determine the true average number of alcoholic drinks consumed by Greek students is conducted.
Standard Deviation, σ = 6.3
Margin Error of population mean, E = 0.5
Probability = 95% = 0.95
The p-value corresponding to 0.95 probability = (1+0.95)/2 = 0.975
The z-score corresponding to this p-value = 1.96 [from the z-tables]
Now, The margin error, E = zσ/√n, where n is the sample size
⇒ n = (zσ/E)²
⇒ n = (1.96 x 6.3/0.5)²
⇒ n ≈ 610
Hence 610 students need to be sampled.
Learn more about z-score at https://brainly.com/question/25638875
#SPJ4
whats the answer for 0.2x-6=11
Answers
Answer:
\(\huge\boxed{\sf x = 85}\)
Step-by-step explanation:
Given equation:0.2x - 6 = 11
Add 6 to both sides0.2x = 11 + 6
0.2x = 17
Divide both sides by 0.2x = 17/0.2
x = 85\(\rule[225]{225}{2}\)
Given:-
\( \rm \: 0.2x - 6 = 11\)\( \: \)
Solution:-
\( \rm{0.2x - 6 = 11}\)\( \: \)
\( \rm \: 0.2x = 11 + 6\)\( \: \)
\( \rm \: 0.2x = 17\)\( \: \)
\( \rm \: x = \cancel \frac{17}{0.2} \)\( \: \)
\( \underline { \boxed{ \rm \color{skyblue} \: x = 85 \: }}\)\( \: \)
\( \purple {━━━━━━━━━━━━━━━━━━━━━━━━━━━━}\)
hope it helps!
studious athletes a university is concerned about the academic standing of its intercollegiate athletes. a study committee chooses an srs of 50 of the 316 athletes to interview in detail. suppose that 40% of the athletes have been told by coaches to neglect their studies on at least one occasion. what is the probability that at least 15 in the sample are among this group?
Answers
The probability that at least 15 in the sample are among this group is given as follows:
0.9441 = 94.41%.
How to obtain probabilities using the normal distribution?The z-score of a measure X of a variable that has mean symbolized by \(\mu\) and standard deviation symbolized by \(\sigma\) is obtained by the rule presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The binomial distribution is the probability of x successes on n trials, with p probability of a success on each trial. It can be approximated to the normal distribution with \(\mu = np, \sigma = \sqrt{np(1-p)}\).
The parameters for the binomial distribution are given as follows:
n = 50, p = 0.4.
Hence the mean and the standard deviation for the approximation are of:
\(\mu = np = 50 \times 0.4 = 20\)\(\sigma = \sqrt{np(1-p)} = \sqrt{50 \times 0.4 \times 0.6} = 3.46\)Using continuity correction, the probability that at least 15 in the sample are among this group is one subtracted by the p-value of Z when X = 14.5, hence:
\(Z = \frac{X - \mu}{\sigma}\)
Z = (14.5 - 20)/3.46
Z = -1.59
Z = -1.59 has a p-value of 0.0559.
1 - 0.0559 = 0.9441 = 94.41%.
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
QuestionSelect the graph with the final image of ABC after the given sequence of transformations. Rotate ABC90° clockwise about the origin and then reflected over the x-axis.
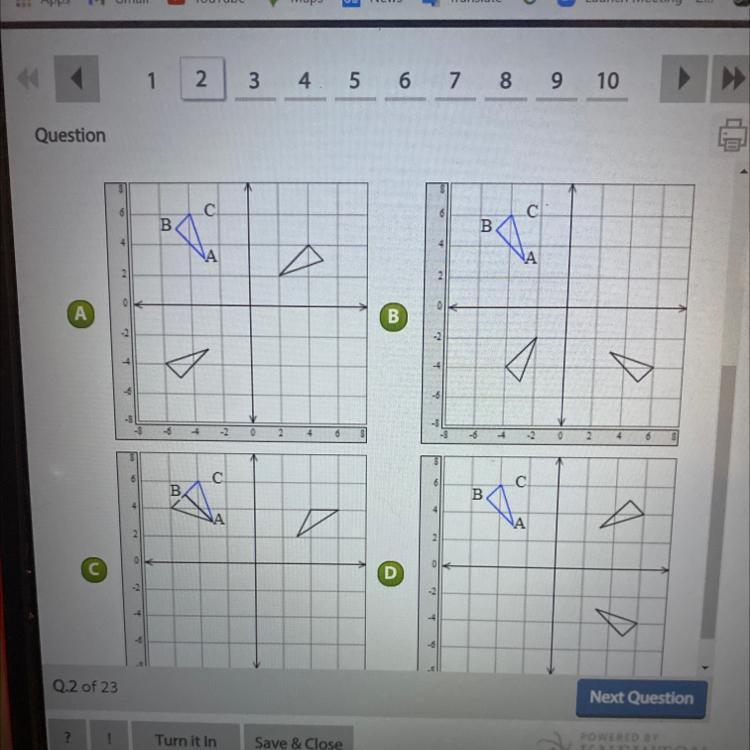
Answers
So first of all we need to list the three points A, B and C so we can properly calculate the transformation:
\(\begin{gathered} A=(-3,3) \\ B=(-5,5) \\ C=(-4,6) \end{gathered}\)The first transformation we have to perform is a 90° clockwise rotation about the origin. If we perform this rotation on a point (x,y) we get:
\((x,y)\rightarrow(y,-x)\)Then we apply this to A, B and C:
\(\begin{gathered} A=(-3,3)\rightarrow A^{\prime}=(3,3) \\ B=(-5,5)\rightarrow B^{\prime}=(5,5) \\ C=(-4,6)\rightarrow C^{\prime}=(6,4) \end{gathered}\)Then we must perform a reflection over the x-axis on the points of triangle A'B'C'. A reflection over the x-axis is achieved by applying this transformation:
\((x,y)\rightarrow(x,-y)\)If we transform points A', B' and C' with this we get:
\(\begin{gathered} A^{\prime}=(3,3)\rightarrow A^{\prime}^{\prime}=(3,-3) \\ B^{\prime}=(5,5)\rightarrow B^{\prime\prime}=(5,-5) \\ C^{\prime}=(6,4)\rightarrow C^{\prime\prime}=(6,-4) \end{gathered}\)Then if we graph all the three triangles in the same grid we get the following picture:
As you can see this image is the same as the one in option D. This means that the answer to this question is graph D.

The graph of the function f(x) = 5 cos (2x) is a reflection over the x-axis of the graph of g(x) =
Answers
Answer:
\(g(x)=-5\cos (2x)\)
Step-by-step explanation:
The given function is
\(f(x)=5\cos (2x)\)
If a function reflected over the x-axis, then x-coordinate remains same but the sign of y-coordinate is changed.
\(P(x,y)\Rightarrow P'(x,-y)\)
If function f(x) is a reflection over the x-axis to get the of g(x), then the resultant function is
\(g(x)=-f(x)\)
Substituting the value of function f(x), we get
\(g(x)=-5\cos (2x)\)
Therefore, the required function is \(g(x)=-5\cos (2x)\).
Hello Freinds
Pls answer
1 micron is equal to ?
the right answer will be marked as brainlist! ✌
Answers
Answer:
Step-by-step explanation:
1 micron = 1 * \(10^{-3} \ milli meter = \frac{1}{1000} \ millemeter\)
1 micron = 0.00003937 inches
Answer:
hello good morning ✌☺
I hope you are fine ❗
its may help you !!!!¡¡¡¡¡¡¿¿¿¿¿¿♤♤♤
llxXKHaNZaDaXxll 《《~_^)⌐╦╦═─

need some help (Geo)

Answers
Answer:
b
Step-by-step explanation:bb
Step-by-step explanation:
Angle 6 and Angle 3 must be supplementary to show that the 2 lines are parallel (D).
Select all pairs of corresponding angles. assume the lines are parallel.
none
2 and 5
1 and 5
4 and 8
1 and 6
4 and 7
2 and 6
3 and 8
3 and 7

Answers
Answer:
1 and 5
2 and 6
3 and 7
4 and 8
What is the greatest
common factor (GCF)
of 18 and 54?
Answers
Answer:
GCF of 18 and 54 is 18.
Step-by-step explanation:
Which inequality represents the sentence? the sum of negative 3.2 and 1.5 times a number is a maximum of 8.6. â€""3.2n 1.5 less-than-or-equal-to 8.6 â€""3.2n 1.5 greater-than-or-equal-to 8.6 â€""3.2 1.5n less-than-or-equal-to 8.6 3.2 1.5n less-than-or-equal-to 8.6
Answers
Inequality (C) -3.2 + 1.5n ≤ 8.6 correctly represents the sentence "the sum of negative 3.2 and 1.5 times a number is a maximum of 8.6."
What is inequality?In mathematics, "inequality" refers to a relationship between two expressions or values that are not equal to one another.
Both mathematical phrases, equations, and inequalities are created by connecting two expressions.
The equal sign (=) indicates that two expressions in an equation are believed to be equivalent.
The symbols >, <, ≤ or ≥ indicate that the two expressions in inequality are not always equal.
So, the sentence we have is:
the sum of negative 3.2 and 1.5 times a number is a maximum of 8.6
Which can be written in inequality as:
-3.2 + 1.5n ≤ 8.6
Therefore, inequality (C) -3.2 + 1.5n ≤ 8.6 correctly represents the sentence "the sum of negative 3.2 and 1.5 times a number is a maximum of 8.6."
Know more about inequality here:
https://brainly.com/question/28964520
#SPJ4
Correct question:
Which inequality represents the sentence?
the sum of negative 3.2 and 1.5 times a number is a maximum of 8.6.
a. -3.2n + 1.5 less-than-or-equal-to 8.6
b. -3.2n - 1.5 greater-than-or-equal-to 8.6
c. -3.2 + 1.5n less-than-or-equal-to 8.6
d. -3.2 - 1.5n less-than-or-equal-to 8.6
A veterinarian knows that a 50-pound dog gets 0.5 milligram of a certain medicine, and that the number of milligrams, m, varies directly with the weight of the dog, w. The vet uses these steps to find the amount of medicine to give a 10-pound dog. Step 1 Find the constant of variation. Step 2 Write the direct variation equation. Step 3 Substitute 10 into the equation to find the dosage for a 10-pound dog. Step 4 Solve for w. The 10-pound dog needs 1000 milligrams. In which step did the veterinarian make the first error? Step 1 Step 2 Step 3 Step 4
Answers
1. Divide the amount needed by the weight:
0.5 milligram / 50 pounds = 0.01 milligram per pound.
2. m = 0.01w
3. m = 0.01(10)
4 m = 0.01 x 10
0.1 milligrams
The error was step 1.
Answer:
Step 3
Step-by-step explanation:
They put the 10 in the wrong place.
Hey um can somone help me out please i dont know what is correct and wrong

Answers
2. Calculator Boy is correct, while Mathy Girl is wrong. After Calculator Boy distributed the 2, he correctly calculated that the 8x could not be subtracted by the “-6 -7”. It left his equation with “8x -13” as the -6 and -7 would combine. Mathy Girl distributed correctly as well, however, she wrote that you could subtract the “-6” from the “8x” which cannot happen. The -6 does not have a variable (x), so it cannot subtract from the “8x”.
I apologize if the explanation is a bit confusing… comment if you would like extra help and I can try to explain it differently!
Suppose that f(x) is differentiable for all x and that 2 ≤ f'(x) ≤ 5. If f(-3) = -1, use the Mean Value Theorem to determine the largest and smallest possible values of f(4). [6] 2. For f(x) = 3x¹ + 4x³, determine the critical points and then determine the intervals of increase and decrease. Use the intervals of increase and decrease to classify any [7] critical points as being local maxima/minima or neither.
Answers
After considering the given data we conclude that the answer for the sub questions are
a) the smallest possible value of f(4) is -1 + 7(2) = 13, and the largest possible value of \(f(4) is -1 + 7(5) = 34\).
b) Since f'(x) is defined for all x, there are no critical points where f'(x) does not exist.
c) Therefore, the critical points are local maxima at x = -1/2 and x = 1/2.
a) To determine the largest and smallest possible values of f(4) using the Mean Value Theorem, we need to find a number c in the interval (-3,4) such that \(f'(c) = (f(4) - f(-3))/(4 - (-3)).\) Since f(x) is differentiable for all x and \(2 \leq f'(x) \leq 5\), we know that \(14 \leq 7f'(c) \leq 35\). Rearranging the equation, we get \(f(4) = f(-3) + 7f'(c)\). Substituting f(-3) = -1, we get \(f(4) = -1 + 7f'(c).\) Therefore, the smallest possible value of f(4) is -1 + 7(2) = 13, and the largest possible value of \(f(4) is -1 + 7(5) = 34.\)
b) For \(f(x) = 3x^1+ 4x^3\), we need to find the critical points and determine the intervals of increase and decrease. Taking the derivative of f(x), we get \(f'(x) = 3 + 12x^2\). Setting f'(x) = 0, we get \(3 + 12x^2 = 0\), which gives \(x =\pm \sqrt(1/4) = \pm1/2.\) Since f'(x) is defined for all x, there are no critical points where f'(x) does not exist.
c) To determine the intervals of increase and decrease, we can use the first derivative test. Since \(f'(x) = 3 + 12x^2 > 0 for x < -1/2 and x > 1/2\), f(x) is increasing on (-∞,-1/2) and (1/2,∞). Since f'(x) < 0 for -1/2 < x < 1/2, f(x) is decreasing on (-1/2,1/2).
Therefore, the critical points are local maxima at x = -1/2 and x = 1/2.
To learn more about Mean Value Theorem
https://brainly.com/question/30403137
#SPJ4
Which sentences represent the inequality? check all that apply. 2.1 (-1.2x) greater-than-or-equal-to 8 the sum of 2.1 and –1.2 times a number is at least 8. the sum of 2.1 and –1.2 times a number is no more than 8. the sum of 2.1 and –1.2 times a number is a maximum of 8. the sum of 2.1 and –1.2 times a number is greater than or equal to 8. the sum of 2.1 and –1.2 times a number is a minimum of 8.
Answers
The best interpretation is that the sum of 2.1 and –1.2 times a number is greater than or equal to 8.
Inequality functionsInequality are expressions not separated by an equal sign, Given the inequality;
2.1 + (-1.2x) ≥ 8
The sign ≥ means greater than or equal to
The expression 2.1 + (-1.2x) ≥ 8 can also be expressed as 2.1 - 1.2x ≥ 8
The best interpretation is that the sum of 2.1 and –1.2 times a number is greater than or equal to 8.
Learn more on inequality here: https://brainly.com/question/11613554
#SPJ4
Answer:
The 1st, 4th, and 5th
Step-by-step explanation:
Find the sum.
10+12+14+...+78
Answers
Answer:
1540
Step-by-step explanation:
This is an arithmetic progression.
a = first term = 10
Common difference = d = second term - first term
= 12 - 10
d = 2
Last term = l = 78
First we have to find how many terms are there in the sequence using the formula: l = a + (n-1)*d
78 = 10 + (n -1) * 2
78 -10 = (n -1)*2
68 = (n -1) *2
68 ÷2 = n -1
34 = n - 1
34 + 1 = n
n = 35
There are 35 terms.
\(\sf \boxed{\test{\bf Sum = $\dfrac{n}{2}(a +l)$}}\)\(\sf \boxed{\text{\bf Sum =$\dfrac{n}{2}(a+l) $}}\)
\(\sf =\dfrac{35}{2}(10+78)\\\\ =\dfrac{35}{2}*88\\\\ = 35 * 44\\\\= 1540\)
Step-by-step explanation:
This is an arithmetic progression.
a = first term = 10
Common difference = d = second term - first term
= 12 - 10
d = 2
Last term = l = 78
First we have to find how many terms are there in the sequence using the formula: l = a + (n-1)*d
78 = 10 + (n -1) * 2
78 -10 = (n -1)*2
68 = (n -1) *2
68 ÷2 = n -1
34 = n - 1
34 + 1 = n
n = 35
There are 35 terms.
\sf \boxed{\test{\bf Sum = $\dfrac{n}{2}(a +l)$}} \sf \boxed{\text{\bf Sum =$\dfrac{n}{2}(a+l) $}}
Sum =
2
n
(a+l)
\begin{gathered}\sf =\dfrac{35}{2}(10+78)\\\\ =\dfrac{35}{2}*88\\\\ = 35 * 44\\\\= 1540\end{gathered}
=
2
35
(10+78)
=
2
35
∗88
=35∗44
=1540
please help me with this

Answers
Answer:
a. range: 4
b. 5 students
c. mean: 8
Step-by-step explanation:
range: subtract the smallest number from the largest number in the data.
10 - 6 = 4
students amount was counted by the number of marks given.
mean: add the data together. (40) divide the sum by the number of marks provided. (5)
40 divided by 5 equals 8
Answer:
4 244 8
Step-by-step explanation:
10 - 6 = 4 is the range
6x5 = 30 7x4 = 28 8x7 = 56 9x10 = 90 10x4 = 40 244 students
mean = 6+7+8+9+10 = 40/5 = 8
Is this correct?
Select the appropriate words to complete the following statements.
A. (Wider) (Narrower) (Stays the same)
(Up) (Down) (Stays the same)
B. (Wider) (Narrower) (Stays the same)
(Up) (Down) (Stays the same)

Answers
h(x) is wider than f(x) and translated 1 unit up.
g(x) is narrower than f(x) and translated 3 units down.
What is translation?It is the movement of the shape in the left, right, up, and down directions.
The translated shape will have the same shape and shape.
There is a positive value when translated to the right and up.
There is a negative value when translated to the left and down.
We have,
a)
f(x) = x²
h(x) = 3x² + 1
This means,
f(x) is dilated with a scale factor of 3 and translated one unit up.
So,
h(x) will be wider than f(x).
b)
f(x) = x²
g(x) = (1/2)x² - 3
This means,
f(x) is dilated with a scale factor of 1/2 and translated to 3 units down.
So,
g(x) will be narrower than f(x).
Thus,
h(x) is wider than f(x) and translated 1 unit up.
g(x) is narrower than f(x) and translated 3 units down.
Learn more about translation here:
https://brainly.com/question/12463306
#SPJ1
A watch company is developing packaging for its new watch. the designer uses an octagonal prism with a base area of 30 in2 and rectangles with a length of 10 in to create a prototype for the new package. what is the volume of the prototype? 140 in3 200 in3 240 in3 300 in3
Answers
The volume of the given prototype is calculated as: Option D: 300in³
How to find the volume of the prototype?We are told that a watch company is developing packaging for its new watch. the designer uses an octagonal prism with a base area of 30 in² and rectangles with a length of 10 in to create a prototype for the new package.
Since the designer uses octagons with a base area of 30 in² and rectangles with a length of 10 in to create a prototype for the new package.
So here the volume is
= 30(10)
= 300
Therefore, The volume of the prototype is 300in³
Read more about Volume at; https://brainly.com/question/17481620
#SPJ1
I'll give brainiest to the first person to respond BUT only if the answer is correct

Answers
Answer:
115 and 1/2
Step-by-step explanation:
B•W•H
Hope this helps! ;-)
Thanks for correcting my mistake!!!
Answer: The answer is 115 1/2
Explanation: Just multiply all the dimensions
The high temperatures for several days are shown in the table.
Which answer describes the average rate of change from day 3 to day 5?
Responses
The high temperature changed by an average of −3 degrees per day from day 3 to day 5.
The high temperature changed by an average of , negative 3, degrees per day from day 3 to day 5.
The high temperature changed by an average of −6 degrees per day from day 3 to day 5.
The high temperature changed by an average of , negative 6, degrees per day from day 3 to day 5.
The high temperature changed by an average of −4 degrees per day from day 3 to day 5.
The high temperature changed by an average of , negative 4, degrees per day from day 3 to day 5.
The high temperature changed by an average of −2 degrees per day from day 3 to day 5.
The high temperature changed by an average of , negative 2, degrees per day from day 3 to day 5.
Day High Temperature (degrees Fahrenheit )
1 67
2 63
3 59
4 58
5 53
Answers
Okay, let's calculate the average rate of change:
On day 3, the high temperature was 59 degrees.
On day 5, the high temperature was 53 degrees.
So the temperature change from day 3 to day 5 was 59 - 53 = 6 degrees.
And the number of days was 5 - 3 = 2 days.
So the average rate of change = (6 degrees) / (2 days) = 3 degrees per day
The closest choice is:
The high temperature changed by an average of −4 degrees per day from day 3 to day 5.
So the answer is:
5
pls help asap if you can!!!!!

Answers
Answer:
x = 24
Step-by-step explanation:
if a and b are parallel then
62 and 5x - 2 are same- side interior angles and sum to 180° , that is
5x - 2 + 62 = 180
5x + 60 = 180 ( subtract 60 from both sides )
5x = 120 ( divide both sides by 5 )
x = 24
thus for a to be parallel to b , then x = 24
find the taylor polynomial t3(x) for the function f centered at the number a. f(x) = e−3xsin 2x, a = 0
Answers
Therefore, the Taylor polynomial T₃(x) for the function f(x) = e^(-3x) * sin(2x) centered at a = 0 is given by T₃(x) = -3x - 6x² - 6x³.
To find the Taylor polynomial T₃(x) for the function f(x) = e^(-3x) * sin(2x) centered at a = 0, we need to calculate the derivatives of f(x) at x = 0 and use them to construct the polynomial.
First, let's find the derivatives of f(x):
f(x) = e^(-3x) * sin(2x)
f'(x) = (-3e^(-3x) * sin(2x)) + (2e^(-3x) * cos(2x))
= e^(-3x) * (-3sin(2x) + 2cos(2x))
f''(x) = e^(-3x) * (9sin(2x) - 12cos(2x))
f'''(x) = e^(-3x) * (-27sin(2x) - 36cos(2x))
Next, let's evaluate these derivatives at x = 0:
f(0) = e^0 * sin(0) = 0
f'(0) = e^0 * (-3sin(0) + 2cos(0)) = -3
f''(0) = e^0 * (9sin(0) - 12cos(0)) = -12
f'''(0) = e^0 * (-27sin(0) - 36cos(0)) = -36
Now, we can construct the Taylor polynomial T₃(x) using the derivatives:
T₃(x) = f(0) + f'(0)(x - a) + f''(0)(x - a)²/2! + f'''(0)(x - a)³/3!
= 0 - 3x + (-12)(x - 0)²/2! + (-36)(x - 0)³/3!
Simplifying further:
T₃(x) = -3x - 6x² - 6x³
To know more about Taylor polynomial,
https://brainly.com/question/30258832
#SPJ11
Graph the line with slope 1 passing through the point (-2,-5).
graph the line please

Answers
A slope of 1 means that for each time x increases by 1, y also increases by 1.
Since a line is uniquely defined by two points, it is sufficient to draw the line passing through (-2, -5) and (-1, -4).
What is Metric and Imperial System?
Answers
The metric system is defined as the decimal system of units based on the meters, kilograms, and second as the units of length, mass, and time respectively. The imperial system is defined as the measurement system used in countries like the UK, Liberia, Myanmar, etc. that uses units like an inch, pound, ton etc.
The Metric and Imperial systems are both systems of measurement. That is, they are not just one unit of measure, but are correlated systems of many units of measure – measuring length and area, weight and mass, volume, force, temperature etc.
The imperial system of measurement is defined as a system that originated in Britain and came to formal use in the early 19th century with the Weights and Measures Act of 1824 and 1878. It uses some of the commonly used units there like an inch, ton, pound, gallon, pint, etc.
Most countries use the metric system which uses the measuring units such as meters and grams, and adds prefixes like kilo, milli, and centi to count orders of magnitude.
To read more about Measurement Units:
https://brainly.com/question/777464
Suppose Z follows the standard normal distribution. Calculate the following probabilities using the ALEKS calculator. Round your responses to at least three decimal places. (a) P(Z < 0.79) = Х 5 ? (b) P(Z > 0.75) (c) P(-1.06 < Z< 2.17) =
Answers
The probabilities Z > 0.75 is P(Z > 0.75) = 1 - P(Z < 0.75).
The probability of Z > 0.75 is 1 - 0.77337 = 0.22663
The probability of Z < -1.06 from it. P(-1.06 < Z< 2.17) = P(Z < 2.17) - P(Z < -1.06) = 0.98425 - 0.14457 = 0.83968
Suppose Z follows the standard normal distribution. The probabilities using the ALEKS calculator are given below.(a) P(Z < 0.79) = 0.78524. (rounded to 5 decimal places)(b) P(Z > 0.75) = 1 - P(Z < 0.75) = 1 - 0.77337 = 0.22663. (rounded to 5 decimal places)(c) P(-1.06 < Z< 2.17) = P(Z < 2.17) - P(Z < -1.06) = 0.98425 - 0.14457 = 0.83968. (rounded to 5 decimal places). In the standard normal distribution, the mean is equal to zero and the standard deviation is equal to 1. The notation for a standard normal random variable is z. Z is a random variable with a standard normal distribution and P(Z) denotes the probability of the random variable Z. Suppose z follows a standard normal distribution then the probability of Z < 0.79 is P(Z < 0.79) = 0.78524. So, the answer is 0.78524(rounded to 5 decimal places).Suppose z follows a standard normal distribution then the probability of Z > 0.75 is P(Z > 0.75) = 1 - P(Z < 0.75). Therefore, the probability of Z > 0.75 is 1 - 0.77337 = 0.22663(rounded to 5 decimal places).Therefore, the probability of -1.06 < Z< 2.17 can be found by finding the probability of Z < 2.17 and then subtracting the probability of Z < -1.06 from it. P(-1.06 < Z< 2.17) = P(Z < 2.17) - P(Z < -1.06) = 0.98425 - 0.14457 = 0.83968(rounded to 5 decimal places).
Learn more about Probabilities
brainly.com/question/30034780
#SPJ11
find the measure of the missing angle
a=

Answers
10. The angle measures of a triangle are shown in the diagram below.
(2x +1)°
(5x +5)
What is the value of x?
x = 25
x = 14
x = 12
X= 7

Answers
X=12
Heheheh
What outcome is likely to occur for a hypothesis test evaluating a treatment that has a very large and robust effect?
Answers
For the given statement, we have to correctly rejecting the null hypothesis.
According to the statement
we have to find the outcome when hypothesis test evaluating a treatment that has a very large and robust effect.
For this purpose, we know that the
A hypothesis is a testable statement about the relationship between two or more variables or a proposed explanation for some observed phenomenon.
And according to the given statement it is clear that the by this we have to rejected this hypothesis.
because this treatment and the large effects are not possible for the independent values of the hypothesis.
In other words, we can say that the we have to correctly rejecting the null hypothesis.
So, For the given statement, we have to correctly rejecting the null hypothesis.
Learn more about hypothesis here
https://brainly.com/question/11555274
#SPJ4
The Center for Disease Control and Prevention reports that 25% of bay boys 6-8 months old in the United States weigh more than 20 pounds. A sample of 16 babies is studied.
Answers
Okay, it seems like you want to analyze a sample of 16 babies based on their weight.
The information you provided states that the Center for Disease Control and Prevention reports that 25% of baby boys aged 6-8 months in the United States weigh more than 20 pounds.
However, you haven't mentioned the specific question or analysis you want to perform on the sample. Could you please clarify what you would like to know or do with the given information?
To know more about Prevention visit-
brainly.com/question/30892272
#SPJ11
22
A rectangle's perimeter and its area have the same numerical value. The width of the rectangle is 3 units. What is
the length of the rectangle in UNS
Record your answer and fill in the bubbles on your answer document. Be sure to use the correct place value.
Answers
2.(x+3) = x×3.
2x + 6 = 3x.
x = 6 units is the answer :)