What is the value of x in this equation?
Х/2 - x = x/4 + 6
Answers
Х/2 - x = x/4 + 6
1/2x - x = 1/4x + 6
-1/2x=1/4x+6
-2x=x+24
-2x-x=24
-3x=24
X=-8
Related Questions
Please answer, will give 5 star.

Answers
Answer:
The first one
Step-by-step explanation:
She cant buy anything over $15, but she can buy something thats $15 :))
please help:)
write an equation of the line , in point slope form, that passes through the two given points.
Points:(-2,10),(10,-14)
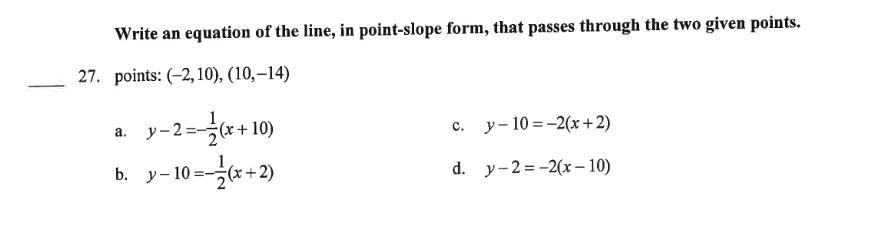
Answers
Answer:
y+2 = (-1/2)(x-3)
Step-by-step explanation:
7. A floor is covered by 800 tiles measuring 10 squared cm. How many square tiles of side 8 cm would be needed to cover the same floor?
Answers
Answer:
1000 tiles
Step-by-step explanation:
Determine total floor space
800 x 10 = 8000 squared cm total floor space.
Divide floor space by size of tile
8000 / 8 = 1000 tiles now required to cover the floor.
Given m∥n, find the value of x.

Answers
Answer:
x = 11
Step-by-step explanation:
The two angles measuring (7x + 14)° and (9x - 8)° are corresponding angles, which are always congruent to each other and thus equal to each other.
Step 1: Thus, we can find the value of x by setting the two angles equal to each other:
7x + 14 = 9x - 8
7x + 22 = 9x
22 = 2x
11 = x
Optional Step 2: We can check that we've found the correct answer by plugging in 11 for x in both (7x + 14) and (9x - 8) and checking that we get the same number:
7(11) + 14 = 9(11) - 8
77 + 14 = 99 - 8
91 = 91
At Westville High School there are 315 seniors and 389 juniors 65%. of the seniors have parking passes and 42% of the juniors have parking passes. The statistics teacher selects a SRS of 30 seniors and a separate SRS of 30 juniors. Let be the difference in the sample proportions of seniors and juniors that have parking passes. a. What is the shape of the sampling distribution of Why? b. Find the mean of the sampling distribution. c. Calculate and interpret the standard deviation of the sampling distribution. d. What is the probability that the difference in sample proportions (senior - junior) of students with parking passes is greater than ?
Answers
(a) Since all values are greater than 10, the sampling distribution is normally distributed.
(b) The mean of the sampling distribution is 0.23.
(c) The standard deviation of the sampling distribution is 0.1288.
(d) The probability that the difference in sample proportions (senior - junior) of students with parking passes is greater than 30% is -0.56.
In the given question, at Westville High School there are 315 seniors and 389 juniors.
65% of the seniors have parking passes and 42% of the juniors have parking passes.
The statistics teacher selects a SRS of 30 seniors and a separate SRS of 30 juniors.
Let be the difference in the sample proportions of seniors and juniors that have parking passes.
(a) We have to find the shape of the sampling distribution.
n1*p1 = 0.65*30 = 19.5 > 10
n1*(1 - p1) = (1 - 0.65)*30 = 10.5 > 10
n2*p2 = 0.42*30 = 12.6 > 10
n2*(1 - p2) = (1 - 0.42)*30 = 17.4 > 10
Since all values are greater than 10, the sampling distribution is normally distributed.
(b) We have to find the mean of the sampling distribution.
Mean = p1 - p2
Mean = 0.65 - 0.42
Mean = 0.23
(c) We have to calculate and interpret the standard deviation of the sampling distribution.
Pooled proportion, P' = (x1 + x2)/(n1 + n2)
P' = (0.65*30 + 0.42*30)/(30 + 30)
P' = 0.535
Standard deviation = √P'(1-P')*(1/n1 + 1/n2)
Standard deviation = √0.535(1- 0.535)*(1/30 + 1/30)
Standard deviation = 0.1288
(d) We have to find the probability that the difference in sample proportions (senior - junior) of students with parking passes is greater than 30%.
The test statistic, z = Mean - delta/√P'(1- P')*(1/n1 + 1/n2)
z = 0.23 - 0.30/0.1288
z = -0.56
The p-value is 0.7118. [Using NORMSDIST(z-value)]
To learn more about sampling distribution link is here
brainly.com/question/13501743
#SPJ4
What is the value of m? 4m=32
Answers
Answer:
m=8
Step-by-step explanation:
To find m divide both sides by 4
4m/4=32/4, then simplify
m=8
How many significant figures are in the number
43.6? 43.6 has [?] significant figures.
Answers
Answer:
43.6 has 3 significant figures.
Use the diagram below to answer the questions about the Law of Cosines.

Answers
Based on the Law of Cosines; it was proven that:
cos Θ = x/acos (180 - C) = x/aa² + b² + 2bx = c²Please note that the given equation on number 3 is wrong. The correct equation should be: a² + b² + 2bx = c². The explanation why the given equation is incorrect will be explained later.
Based on the unshaded triangle, we can find that:
cos Θ = x/a
Next, we will prove that: cos (180 - C) = x/a
Remember that:
cos (A + B) = cos A cos B - sin A sin B
Law of Cosines: c² = a² + b² - 2ab. cos C
cos C = - [c² - (a² + b²)] /2ab ... (i)
Then:
cos Θ = cos (180 - C)
cos (180 - C) = cos 180 . cos C - sin 180 . sin C
We subtitute equation (i):
cos (180 - C) = (-1) (- [c² - ((a² + b²)] / 2ab) - 0 sin C
cos (180 - C) = [c² - (a² + b²)]/ 2ab ... (ii)
If we focus on the unshaded triangle, we can find an equation of a, where:
a² = h² + x² ... (iii)
And if we combine both triangle into a giant triangle, we can make another equation of c. where:
c² = (x + b)² + h² ... (iv)
We will subtitute equation (iv) into equation (ii):
cos (180 - C) = [c² - (a² + b²)]/ 2ab
cos (180 - C) = [(x + b)² + h² - (a² + b²)] / 2ab
cos (180 - C) = [x² + b² + 2bx + h² - a² - b²] / 2ab
cos (180 - C) = [x² + 2bx + h² - a²] / 2ab ... (v)
We subtitute equation (iii) into equation (v):
cos (180 - C) = [x² + 2bx + h² - a²] / 2ab
cos (180 - C) = [a² + 2bx - a²] / 2ab
cos (180 - C) = 2bx / 2ab
cos (180 - C) = x/a --> PROVEN!
Next, we will try to show why the given equation of a² + b² - 2bx = c² is incorrect.
We know that:
a² + b² - 2ab cos C = c²
c² = (x + b)² + h²
We will try to find the value of cos C:
a² + b² - 2ab cos C = (x + b)² + h²
a² + b² - 2ab cos C = x² + b² + 2bx + h²
a² - 2ab cos C = a² + 2bx
- 2 ab cos C = 2bx
cos C = - x/a
We will subtitute the value of cos C under the Law of Cosines:
c² = a² + b² - 2ab cos C
c² = a² + b² - 2ab (- x/a)
c² = a² + b² + 2bx --> PROVEN!
Learn more about Law of Cosines here: brainly.com/question/9261858
#SPJ1
Solve -3(5x-9) please
Answers
Answer:
12
Step-by-step explanation:
Which if the following is equivalent to 7-2(x+2)<-4-3(1-x)

Answers
Answer:
The answer is -5x<-10 because the equation is equal to X>2 and answer-5x<-10 is also equal to X>2
Step-by-step explanation:
i will give Brainiest if you are right

Answers
Answer:
i think the answer is C
Determine the whole number of standard deviations from the mean that include all
data values.
The mean price of the nonfiction books on a best-sellers list is $25.07; the standard
deviation is $2.62.
$26.95, $22.95, $24.00, $24.95, $29.95, $19.95, $24.95, $24.00, $27.95, $25.00
Answers
The number of standard deviations from the mean that include all
data values is two.
Standard Deviation could be a live that shows what proportion variation (such as unfold, dispersion, spread,) from the mean exists. the quality deviation indicates a “typical” deviation from the mean.it's a well-liked live of variability as a result of it returns to the initial units of live of the information setFrom the gathering of information, we will see that the minimum worth is $19.95 and also the most worth is $29.95. So , we would like to seek out the amount of normal deviations, let's decision it "a" , such that\(\overline x $\color \ - a\cdot\sigma \le 19.95}\) and \(\overline x $\color \ +a\cdot\sigma \geq 29.95}\)
Use the given values of mean \(\overline x\) and normal deviation (σ) to notice the worth of "a".
\(\overline x $\color \ - a\cdot\sigma \le 19.95}\\25.07\ - 2.62a \leq 19.95\\5.12\leq 2.62a\\1.9541\leq a\)
On rounding off we get a = 2
Checking another inequality
\(\overline x $\color \ + a\cdot\sigma \geq 29.95}\\25.07 \ + 2(2.62) \geq 29.95\\25.07 + 5.24 \geq 29.95\\30.31\geq 29.95\)
Thus , 2 standard deviation include the all values from the given set of data .
Learn more about standard deviation here :
https://brainly.com/question/12402189
#SPJ9
Please complete the math and explain

Answers
Let x be the mass of the liquid itself, and y the mass of the empty bottle. Then
x + y = 1 1/2 kg
x = y + 3/4 kg
Substitute x into the first equation and solve for y :
(y + 3/4 kg) + y = 1 1/2 kg
(y + 3/4 kg) + y = 3/2 kg
2y + 3/4 kg = 3/2 kg
2y = 3/2 kg - 3/4 kg
2y = 6/4 kg - 3/4 kg
2y = (6 - 3)/4 kg
2y = 3/4 kg
y = 3/8 kg
Now solve for x :
x = 3/8 kg + 3/4 kg
x = 3/8 kg + 6/8 kg
x = (3 + 6)/8 kg
x = 9/8 kg
That is, the empty bottle weighs 3/8 kg, and the liquid that fills the bottle 3/4 of the way weighs 9/8 kg.
If the bottle is completely filled, then it contains an amount of liquid weighing z such that 3/4 of z weighs 9/8 kg. Solve for z :
3/4 z = 9/8 kg
z = (9/8)/(3/4) kg
z = (9/8)•(4/3) kg
z = (9•4)/(8•3) kg
z = 36/24 kg
z = 3/2 kg
So, the total weight of the completely filled bottle is
y + z = 3/8 kg + 3/2 kg
y + z = 3/8 kg + 12/8 kg
y + z = (3 + 12)/8 kg
y + z = 15/8 kg
Calculate each compound event probability: a. X ≤ 15, n = 20, π = .70 (Round your answer to 4 decimal places.) b. X > 8, n = 11, π = .65 (Round your answer to 4 decimal places.) c. X ≤ 1, n = 13, π = .40 (Round your answer to 4 decimal places.)
Answers
For X ≤ 15, n = 20, π = .70 ; compound event probability is approximately 0.0008 .
For X > 8, n = 11, π = .65 ; compound event probability is approximately 0.9198.
For X ≤ 1, n = 13, π = .40 ; compound event probability is approximately 0.6646 .
a. To calculate the probability of the event X ≤ 15, n = 20, π = .70, we will use the binomial distribution formula:
P(X ≤ 15)
= ∑_(k=0)¹⁵〖(20Ck)(0.70)^k (0.30)^(20-k) 〗
Using a binomial distribution calculator, we can find this probability to be approximately 0.0008 (rounded to 4 decimal places).
b. To calculate the probability of the event X > 8, n = 11, π = .65, we will first find the probability of X ≤ 8, and then subtract this value from 1 to find the complement probability:
P(X > 8) = 1 - P(X ≤ 8)
= 1 - ∑_(k=0)⁸〖(11Ck)(0.65)^k (0.35)^(11-k)〗
Using a binomial distribution calculator, we can find the probability of X ≤ 8 to be approximately 0.0802.
Therefore, the probability of X > 8 is approximately 0.9198 (rounded to 4 decimal places).
c. To calculate the probability of the event X ≤ 1, n = 13, π = .40, we will use the binomial distribution formula:
P(X ≤ 1)
= ∑_(k=0)¹〖(13Ck)(0.40)^k (0.60)^(13-k)〗
Using a binomial distribution calculator, we can find this probability to be approximately 0.6646 (rounded to 4 decimal places).
For more such questions on event probability visit:
https://brainly.com/question/30390037
#SPJ8
which expression is represented by the pharase "the square of y decreased by the quotient of 28 and 7"?
Answers
Answer:
y^2 - 28/7
Step-by-step explanation:
Need help asap!
Solve the following system of equations and show all work. y = −x2 + 4 y = 2x + 1
Answers
Answer:
The solutions to the given system of equations are:
x = 1, y = 3x = -3, y = -5Step-by-step explanation:
Given system of equations:
\(\begin{cases}y=-x^2+4\\y=2x+1\end{cases}\)
To solve the given system of equations, substitute the second equation into the first equation:
\(\implies 2x+1=-x^2+4\)
Add x² to both sides:
\(\implies x^2+2x+1=4\)
Subtract 4 from both sides:
\(\implies x^2+2x-3=0\)
Factor the quadratic equation:
\(\implies x^2+3x-x-3=0\)
\(\implies x(x+3)-1(x+3)=0\)
\(\implies (x-1)(x+3)=0\)
Apply the zero product property:
\((x-1)=0 \implies x=1\)
\((x+3)=0 \implies x=-3\)
Substitute the found values of x into the second equation and solve for y:
\(x=1 \implies y=2(1)+1=3\)
\(x=-3 \implies y=2(-3)+1=-5\)
Therefore, the solutions to the given system of equations are:
x = 1, y = 3x = -3, y = -5The diver's actions can be represented by the subtraction equation 3-4 = -1
1. Write a related addition sentence for the subtraction sentence.
Answers
4 + (-1) = 3
Answer:
jdtttttttttttttttttttjjfjyk
Step-by-step explanation:
thanks.
fill in the mission numbers to make the fractions equivalent. 1/2 and /8= 4/12 and /60= 2/3 and /12= 4/4 and /8=
Answers
To make the fractions equivalent, we need to find the missing numerators that would make them equal. Let's fill in the missing numerators:
1/2 and __/8
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 4:
1/2 and 4/8
Now, the fractions are equivalent.
---
4/12 and __/60
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 5:
4/12 and 20/60
Now, the fractions are equivalent.
---
2/3 and __/12
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 4:
2/3 and 8/12
Now, the fractions are equivalent.
---
4/4 and __/8
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 2:
4/4 and 8/8
Now, the fractions are equivalent.
The population of a town is predicted to grow according to the following model:
P = 15e0.012r
where P represents the number of people in thousands and t is the number of years since 2020. Find
the predicted population in the year 2030. Round your answer to nearest person
O 16,912 people
O 16,913 people
O 16 people
O 17 people
Answers
The predicted population in the year 2030 is 10 people
How to determine the predicted population in the year 2030From the question, we have the following parameters that can be used in our computation:
Population function, P(t)= 15е⁻⁰.⁰¹²⁺
Also from the question, we have
The variable t represents the number of years since 2020
This means that the value of t in 2030 is
t = 2030 - 2020
t = 10
So, we have
P(10)= 15е⁻⁰.⁰¹² ˣ ¹⁰
Evaluate the above products
P(10)= 15е⁻⁰.¹²
Evaluate the exponents
P(10)= 13.30
Approximate the above expression
P(10) = 13
This means that the number of people is 13
Read more about exponential functions at
brainly.com/question/11464095
#SPJ1
А
?
Ө
Ө
C
5.5
3
D
2.8
B

Answers
Answer:
58,93.
Step-by-step explanation:
1. the rule is:
AB:AC=BD:CD, then
2. according to the rule above:
5.5:AC=2.8:3, then
AC=55*15/14≈58.93.
Chancellor Manufacturing makes two pumps for use in household reef aquariums. The Standard pump (Model A) requires 4.5 lbs of stainless steel while the Deluxe lightweight pump (Model B) 3.0 lbs of stainless steel. There are 63 lbs of stainless steel available during this production period. The combined production of both pumps must be at least 12 pumps. There are orders for at least 6 of the lightweight Model B. Lastly, management has decided that no more than 15 Model B pumps be produced.
Required:
a. Write the LP formulation which provides the optimal production schedule for the standard and deluxe pumps such that the cost is minimized.
b. Write the above LP formulation in Standard Form.
c. Using your grid page, graph the above LP formulation. Be sure to label axes, constraints, and the feasible region.
Answers
Answer:
The answer is below
Step-by-step explanation:
Chancellor Manufacturing makes two pumps for use in household reef aquariums. The Standard pump (Model A) requires 4.5 lbs of stainless steel while the Deluxe lightweight pump (Model B) 3.0 lbs of stainless steel. There are 63 lbs of stainless steel available during this production period. The combined production of both pumps must be at least 12 pumps. There are orders for at least 6 of the lightweight Model B. Lastly, management has decided that no more than 15 Model B pumps be produced.
The cost to produce one Standard pump is $150 and to produce one Deluxe pump is $210.
Solution:
a) Let x represent model pump A and let y represent model pump B.
Since There are 63 lbs of stainless steel available, hence:
4.5x + 3y ≤ 63
Both pumps must be at least 12 pumps. Therefore:
x + y ≤ 12
There are orders for at least 6 of the lightweight Model B:
y ≥ 6
Also, no more than 15 Model B pumps be produced:
y ≤ 15
The cost to produce one Standard pump is $150 and to produce one Deluxe pump is $210. The cost equation is:
Minimize Cost = 150x + 210y
b)
Hence the LP formation is:
Minimize Cost = 150x + 210y
4.5x + 3y ≤ 63
x + y ≤ 12
y ≥ 6
y ≤ 15
x ≥ 0.
c) The LP problem was solved using geogebra online graphing tool.
The points that satisfy the problem are:
(0, 6), (0,12), (6, 6)
At (0,6); cost = 150(0) + 210(6) = 1260
At (0,6); cost = 150(0) + 210(12) = 2520
At (6,6); cost = 150(6) + 210(6) = 2160
Hence the minimum cost is at (0, 6)

1.4x + 3.5y
help! 6th grade :)
Answers
Answer:
Step-by-step explanation:
Simplifying
1.4x + 3.5y = 0
Solving
1.4x + 3.5y = 0
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-3.5y' to each side of the equation.
1.4x + 3.5y + -3.5y = 0 + -3.5y
Combine like terms: 3.5y + -3.5y = 0.0
1.4x + 0.0 = 0 + -3.5y
1.4x = 0 + -3.5y
Remove the zero:
1.4x = -3.5y
Divide each side by '1.4'.
x = -2.5y
Simplifying
x = -2.5y
If the sum of first n terms of an AP is 3n² + 5n find the AP.
Answers
Let a (n) denote the n-th term in the progression. Consecutive terms in the sequence differ by a fixed constant - call it c - such that
a (n) = a (n - 1) + c
Let a = a (1) be the first term in the sequence. We can solve for a (n) in terms of a alone:
a (n) = a (n - 1) + c
a (n) = (a (n - 2) + c) + c = a (n - 2) + 2c
a (n) = (a (n - 3) + c) + c = a (n - 3) + 3c
and so on, down to
a (n) = a + (n - 1) c
The sum of the first n terms is then
\(\displaystyle\sum_{k=1}^n a(k)=\sum_{k=1}^n(a+(k-1)c)=a\sum_{k=1}^n1+c\sum_{k=1}^n(k-1)=an+\frac{cn(n-1)}2=\frac c2n^2+\left(a-\frac c2\right)n\)
Since this is equal to 3n ^2 + 5n, it follows that
c/2 = 3 => c = 6
a - c/2 = 5 => a = 8
So the sequence is
a (n) = 8 + (n - 1) 6 = 6n + 2
6*9+(6+9)=?
Plz I really need this in the next minute.
Answers
9-3(2x-4)
Answer please
Answers
Answer:
-6x + 21
Step-by-step explanation:
9 - 3(2x - 4)
9 - 6x + 12
-6x + 21
9-6x+12
-6x+21
x=-3.5
graph the parabola x=1/2(y-2)^2-4. find and graph the vertex, focus, directrix, and focal chord endpoints.
Answers
1. Find the graph of the parabola attached below
2. Vertex (-4, 2) Focus (-7/2, 2) Directrix (x = -9/2) Endpoints (-7/2, 1) (-7/2, 3)
How do we find the vertex, focus, directrix, and focal chord endpoints or the parabola?For the parabola, x = 1/2(y-2)² - 4 we will use the equation x = 4p(y-k)² + h,
Vertex → (h, k)
In our given equation, (y - 2) → (y - k), so k = 2. The term on the rightmost side of our equation (-4) → h in the form, so we know h = -4. ∴ vertex (-4, 2).
focus → (h, k) = (-4, 2); P = 1/2
Parabola is symmetric around the x axis and so the focus lies a distance P, from the center, along the x axis.
∴ Focus is (-4 + p, 2)
(-4 + 1/2, 2) ⇒ (-7/2, 2)
directrix → x = d
Parabola is symmetric around the x axis and therefore the directrix is a line paralled to the y axis a distance away from the ceter (-4, 2) x coordinate.
∴ x = -4 - p ⇒ x = -4 - 1/2
x = 9/2
focal chord endpoints →
The focus of the parabola is (-7/2, 2).
The y-coordinate of the focus is 2, so the y-coordinates of the endpoints of the focal chord are 2 + 1 and 2 - 1, → 3 and 1.
Therefore, the endpoints of the focal chord are:
(-7/2, 3) and (-7/2, 1).
Find more exercises on parabola;
https://brainly.com/question/11911877
#SPJ1

i need help on these please

Answers
The cost of gas is proportional to the volume of gas because a constant rate of $3.15 to 1 gallon of gas.
How to calculate the constant rate of gas?From the given table;
The volume of the first gas Layla bought = 3 gallons.
The cost of the 3 gallons = 9.45
Therefore the cost of 1 gallon = ?
That is:
3 gallons = $9.45
1 gallon = X
Make X the subject of formula:
X = 9.45/3 = $3.15
Therefore, the cost of 11 gallons of gas would be = 11×3.15 = $34.65. This is because the cost of 1 gallon would be = $3.15.
Learn more about division here:
https://brainly.com/question/25289437
#SPJ1
Among all pairs of numbers whose sum is 24, find a pair whose product is as large as possible. Show the work(the steps)! Write an equation of the corresponding quadratic function. How parabola opens? What is the maximum product? Does this function has a maximum value or the minimum value? Explain. Graph the function and upload the image.
Answers
The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.
To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.
Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.
To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:
P(x) = x(24 - x)
This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.
The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.
To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.
Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.
So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.
Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.
To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
Barbara has a bunny that weighs 2 pounds and gains 3 pounds per year. Her cat weighs 6 pounds andgains 1 pound per year. When will the bunny and the cat weigh the same amount?
Answers
SOLUTION:
Step 1:
In this question, we are given the following:
Barbara has a bunny that weighs 2 pounds and gains 3 pounds
per year which means:
\(2\text{ + 3y }\)Her cat weighs 6 pounds and gains 1 pound per year which means:
\(\text{ 6 + y}\)When will the bunny and the cat weigh the same amount means:
\(2\text{ + 3y =6 + y}\)collecting like terms, we have that:
\(\begin{gathered} 3y\text{ - y = 6 - 2} \\ 2y\text{ = 4} \\ \text{Divide both sides by 2, we have that:} \\ y\text{ = }\frac{4}{2} \\ y\text{ = 2} \end{gathered}\)CONCLUSION:
The bunny and the cat will weigh the same amount in 2 years' time.
4x - 4 + (-5x + 8 please help