What is the length of segment DF?
B
4/28
1
68°
C
2
А A
2
3
8
4
68°
28°
F
5
Type your answer.

Answers
Answer:
DF = 17.12
Step-by-step explanation:
From the picture attached,
From ΔABC and ΔEFD,
m∠ABC = m∠EFD = 28°
m∠BAC = m∠EDF = 68°
By AA property of similarity, ΔABC and ΔEFD will be similar.
And their corresponding sides will be proportional.
\(\frac{AB}{EF}=\frac{BC}{DF}=\frac{AC}{ED}\)
\(\frac{4}{EF}=\frac{BC}{DF}=\frac{2}{8}\)
\(\frac{4}{EF}=\frac{1}{4}\)
EF = 16
Now by applying cosine rule in ΔDEF,
DF² = ED² + EF² - 2(ED)(EF)cos(E)
DF² = 8² + (16)² - 2(8)(16)cos(84)°
DF² = 320 - 26.76
DF = √(293.24)
DF = 17.12
Related Questions
Xavi wants to measure the impact of using water for irrigation on a stream's flow rate. The flow rates both
upstream and downstream of the irrigation point are normally distributed,
For each location, Xavi selects a random time each month and measures the flow rate in liters per second.
After he has 12 samples per location, he will look at the difference (upstream - downstream) in their
sample means
What do we know about the shape of the sampling distribution of WU - ip, and why?
Answers
Answer:
exactly normal
You can use the formula S = 10mi to approximate the surface area S, in square centimeters, of a horse with mass m, in grams. What is the surface area of a horse with a mass of 4.5 x 10 5 grams? Round your answer to the nearest whole square centimeter.
Answers
The surface area of a horse with the mass is 4.5 x 10^6 square centimeters,
What is the surface area of a horse with the massFrom the question, we have the following parameters that can be used in our computation:
S = 10mi
Where the surface area = S, in square centimeters, Mass = m, in gramsUsing the above as a guide, we have the following:
m = 4.5 x 10^5 grams
substitute the known values in the above equation, so, we have the following representation
S =10 * 4.5 x 10^5
So, we have
S =4.5 x 10^6
Hence, the surfave area is 4.5 x 10^6
Read more about function at
https://brainly.com/question/28277110
#SPJ1
A random Gaussian process x has a mean of 2.5 and variance of 0.36. Calculate the probability of the random variable having a value less than 3.
Answers
Answer: 0.79758
Step-by-step explanation:
Given that :
Mean (m) = 2.5
Variance = 0.36
Thw standard deviation = sqrt(variance) = sqrt(0.36) = 0.6
The probability of the random variable having a value less than 3 is obtained by:
P(x < 3)
Using the relation to obtain the standardized Zscore :
Z = (x - m) / s
Z = (3 - 2.5) / 0.6
Zscore = 0.8333333
p(Z < 0.833) = 0.79758 ( Z probability calculator)
A locker combination consists of three digits. The digits are the numbers
O through 9. Which is the number of possible locker combinations?
Answers
Answer:
729
Step-by-step explanation:
9x9x9
9. What is 3/8x3/8x3/8 written as a power?
Answers
Answer:
3^3/8^3
Step-by-step explanation:
because since there are 3 three's in 3/8, it will have to be 3^3 and since there are 8 three's, it will be 8^3. so the answer will be 3^3/8^3
The representation of the expression (3/8)x.(3/8)x.(3/8)x in terms of power is [(3/8)x]³.
What is a numerical expression?A numerical expression is a mathematical statement written in the form of numbers and unknown variables. We can form numerical expressions from statements.
Given, An expression (3/8)x.(3/8)x.(3/8)x.
= (3/8)×(3/8)×(3/8)×x×x×x.
= (3/8)³×x³.
= [(3/8)x]³.
learn more about numerical expressions here :
https://brainly.com/question/29199574
#SPJ5
CERTAIN ANSWERS!!! Please assist me! I will award you brain crown! Thank you in advance:))

Answers
Answer:
See below.
Step-by-step explanation:
Statements: Reasons:
1) \(\angle 2\cong\angle 3\) Given
2) \(m\angle2=m\angle 3\) Definition of Congruence
3) \(\angle 1\text{ and } \angle 2\text{ form a linear pair}\) Given
4) \(\angle 1 \text{ and } \angle 2\text{ are supplementary}\) Supplement Theorem
5) \(m\angle 1+m\angle 2=180^\circ\) Definition of Supplementary Angles
6) \(m\angle 1+m\angle 3=180&^\circ\) Substitution
7) \(\angle 1\text{ and } \angle 3 \text{ are supplementary}\) Definition of Supplementary
And we're done!
What is the equation for this line?

Answers
y=2/3x-4 is the equation of the line where 2/3 is the slope.
We have to find the equation of line which is passing through points (0, -4) and (3, -2).
The slope intercept form of a line is y=mx+b, where m is slope and b is the y intercept.
The slope of line passing through two points (x₁, y₁) and (x₂, y₂) is
m=y₂-y₁/x₂-x₁.
Slope = -2+4/3-0
=2/3
Now let us find the y intercept.
-4=2/3(0)+b
b=-4
The equation of line is y=2/3x-4.
To learn more on slope of line click:
https://brainly.com/question/16180119
#SPJ1
The population of a city is 100,000. It doubles each decade for 5 decades. Select all
expressions that represent the population of the city after 5 decades.
A. 32,000
B. 320,000
C. 100,000 -2.2.2.2.2
D. 100,000 - 5 with the power of 2
E. 100,000 - 2 with the power of 5

Answers
Answer:
The answer is C and E.
Step-by-step explanation:
I just took the assignment and it is C and E.
The expression that represents the population after 5 decades is
100,000 x \(2^5\) or 100,000 x 2 x 2 x 2 x 2 x 2.
Options C and E is the correct answer.
What is an equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign.
Example:
2x + 4 = 8 is an equation.
We have,
The population of the city = 100,000
Population doubles every decade.
This means,
Population after 1 decade.
= 100,000 x 2
= 200,000
Population after 2 decades.
= 200,000 x 2 x 2
= 800,000
We can write an expression for the population after x decade.
= 100,000 x \(2^x\)
The population after 5 decades.
= 100,000 x \(2^5\)
= 100,000 x 2 x 2 x 2 x 2 x 2
= 100,000 x 32
= 3200,000
Thus,
The expression is 100,000 x \(2^5\) or 100,000 x 2 x 2 x 2 x 2 x 2.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ2
2. 7 cm In triangle ABC, AC = 7 cm, BC = 10 cm, angle ACB = 73° C 73° 10 cm Calculate the length of AB Give your answer correct to 3 significant figures. Diagram NOT accurately drawn B (Total 3 marks

Answers
Answer:
AB = 10.398
Step-by-step explanation:
By cosine rule, we have:
AB² = AC² + BC² - 2(AC)(BC)cos(ACB)
⇒ AB² = 7² + 10² - 2(7)(10)cos(73)
⇒ AB² = 49 + 100 - 140cos(73)
⇒ AB² = 149 - 140cos(73)
⇒ AB² = 149 - 140cos(73)
⇒ AB² = 149 - 140(0.292)
⇒ AB² = 149 - 40.88
⇒ AB² = 108.12
⇒ AB = √(108.12)
⇒ AB = 10.398
According to the last census (2010), the mean number of people per household in the United States is (https://www.census.gov/content/dam/Census/library/publications/2012/dec/c2010br-14.pdfLinks to an external site.). Assume a standard deviation of . You plan to take a random sample of 110 households, what is the probability the sample mean household size is between 2.5 and 2.66 people? (round your probabilities to three decimal places)
Answers
0.738 is the probability the sample mean household.
How does sampling distribution work?
When selecting random samples from a particular population, statisticians create a probability distribution of that statistic, which is known as a sampling distribution.
It reflects the frequency distribution of how widely spaced different outcomes will be for a particular population and is also referred to as a finite-sample distribution.
we have to determine P[ 2.5 < X < 2.66]
μₓ = 2.58
σₓ = σ/√n = 0.75/√110 = 0.07150969
= p[2.5 < x < 2.66]
= P[X < 2.66] - P[X < 2.5]
= P[ X - μₓ/σₓ < 2.66 - 2.58/0.07150969] - P[ X - μₓ/σₓ < 2.50 - 2.58/0.07150969]
= P[ Z < 1.12] -P[Z< -1.12]
= 0.8686 - 0.1314
= 0.737
P[Z< 1.12] - P[Z < -1.12]
= 0.869 - 0.131
= 0.738
Learn more about sampling distribution
brainly.com/question/13501743
#SPJ1
the total flying time for a round trip between city a and city b is 5 h. because of the jet stream, the time going is not equal to the time returning. express the flying time between city a and city b in terms of the flying time t between city b and city a.
Answers
The flying time 't' between city B and city A can be expressed as
t=(5-x)hours.
Total flying time for a round trip between City A and City B = 5 hours
Let the flying time from City A and City B be x hours and the flying time from City B and City A be t hours.
So, the total time taken will be x+t hours.
As the time of going is not equal to the time of returning due to the jet stream, so t≠x.
This expression representing the flying time for a round trip is:
5=x+t
t=5-x
Therefore, the expression representing the flying time 't' between city b and city is t=(5-x) hours.
To know more about time here:
https://brainly.com/question/28712702#
#SPJ4
What is the explicit rule for the geometric sequence 29.7,9.9,3.3,1.1,
Answers
The explicit rule for the geometric sequence 29.7,9.9,3.3,1.1, are as follows,
Here the first term is considered as, a1, is 29.7.
Explicit formulas are used to represent all the terms of the geometric sequence with a single formula.
\(t_{n} = ar^{n-1}\)
The common ratio to be considered as, r is 9.9/29.7 = 1/3.
So, the generic explicit rule is ...
\(a_{n} = a1r^{n-1}\)
By filling the above equation with the above given values you will get the explicit rule ...
So,
\(a_{n} = 29.7(1/3)^{n-1}\)
Hence the answer is \(a_{n} = 29.7(1/3)^{n-1}\)
To learn more about explicit rule click here https://brainly.com/question/28109381
#SPJ9
If 1/x + 1/3х = 5, what is the value of 3x/4
Answers
Answer:
Step-by-step explanation:
\(\frac{1}{x}+\frac{1}{3x}=5\\\\\frac{1*3}{x*3}+\frac{1}{3x}=5\\\\\frac{3}{3x}+\frac{1}{3x}=5\\\\\frac{4}{3x}=5\\\\4=5*3x\\\\4=15x\\\\\frac{4}{15}=x\)
x = 4/15
\(\frac{3}{4}x=\frac{3}{4}*\frac{4}{15}\\\\=\frac{1}{5}\)
Help with math problems

Answers
The vertex form of the quadratic equations in standard form are, respectively:
Case 9: y = 2 · (x + 2)² - 12
Case 10: y = - (1 / 2) · (x + 3 / 4)² + 33 / 32
Case 11: y = 3 · (x - 4 / 3)² - 16 / 3
Case 12: y = - 3 · (x - 3)²
Case 13: y = (x - 4)² + 3
Case 14: y = (x - 1)² - 7
Case 15: y = (x + 3 / 2)² - 9 / 4
Case 16: 2 · (x + 1 / 4)² - 1 / 8
Case 17: y = 2 · (x - 3)² - 7
Case 18: y = - 2 · (x + 1)² + 10
How to derive the vertex form of a quadratic equationIn this problem we find ten cases of quadratic equation in standard form, whose vertex form can be found by a combination of algebra properties known as completing the square. Completing the square consists in simplifying a part of the quadratic equation into a power of a binomial.
The two forms are introduced below:
Standard form
y = a · x² + b · x + c
Where a, b, c are real coefficients.
Vertex form
y - k = C · (x - h)²
Where:
C - Vertex constant(h, k) - Vertex coordinates.Now we proceed to determine the vertex form of each quadratic equation:
Case 9
y = 2 · x² + 4 · x - 4
y = 2 · (x² + 2 · x - 2)
y = 2 · (x² + 2 · x + 4) - 12
y = 2 · (x + 2)² - 12
Case 10
y = - (1 / 2) · x² - 3 · x + 3
y = - (1 / 2) · [x² + (3 / 2) · x - 3 / 2]
y = - (1 / 2) · [x² + (3 / 2) · x + 9 / 16] + (1 / 2) · (33 / 16)
y = - (1 / 2) · (x + 3 / 4)² + 33 / 32
Case 11
y = 3 · x² - 8 · x
y = 3 · [x² - (8 / 3) · x]
y = 3 · [x² - (8 / 3) · x + 16 / 9] - 3 · (16 / 9)
y = 3 · (x - 4 / 3)² - 16 / 3
Case 12
y = - 3 · x² + 18 · x - 27
y = - 3 · (x² - 6 · x + 9)
y = - 3 · (x - 3)²
Case 13
y = x² - 8 · x + 19
y = (x² - 8 · x + 16) + 3
y = (x - 4)² + 3
Case 14
y = x² - 2 · x - 6
y = (x² - 2 · x + 1) - 7
y = (x - 1)² - 7
Case 15
y = x² + 3 · x
y = (x² + 3 · x + 9 / 4) - 9 / 4
y = (x + 3 / 2)² - 9 / 4
Case 16
y = 2 · x² + x
y = 2 · [x² + (1 / 2) · x]
y = 2 · [x² + (1 / 2) · x + 1 / 16] - 2 · (1 / 16)
y = 2 · (x + 1 / 4)² - 1 / 8
Case 17
y = 2 · x² - 12 · x + 11
y = 2 · (x² - 6 · x + 9) - 2 · (7 / 2)
y = 2 · (x - 3)² - 7
Case 18
y = - 2 · x² - 4 · x + 8
y = - 2 · (x² + 2 · x - 4)
y = - 2 · (x² + 2 · x + 1) + 2 · 5
y = - 2 · (x + 1)² + 10
To learn more on quadratic equations in vertex form: https://brainly.com/question/29260906
#SPJ1
A coin toss bet is placed between two friends such that the person who wins four tosses first is the winner. What is the total number of possible ways in which the bet can play out
Answers
Answer:
who wins four tosses first is the winner.
possible cases-7 tosses, 6 tosses, 5 tosses, 4 tosses
We get cases of Win of Head first-4 tosses
All 4 must be Head
Number of ways = 1
5 tosses-5th must be Head
there are 3 Head out of 4 in ⁴C₃ = 4 Ways
6 tosses-6th must be Head
there are 3 Head out of 5 in ⁵C₃ = 10 Ways
7 tosses-7th must be Head
there are 3 Head out of 6 in ⁶C₃ = 20 Ways
Cases of Head wins = 1+ 4 + 10 + 20 = 35
similarly cases when Tails Wins = 35
Total Possible cases = 35 + 35 = 70
70 is total number of possible ways in which the bet can play out.
Step-by-step explanation:
I hope that this helps u out..
Express 602.16 dam in decimeters
Answers
The expression of 602.16 dam in decimeters can be written as 60216 decimeter.
How can the expression of 602.16 dam be converted to decimeters?The concept that will be used in the calculation is conversion. to perform this conversion, it is important to note that 1 Decimeter (dm) is equal to 0.01 dekameter (dam).
Then, if 1dm = 0.01 dam
Xdm = 602.16 dam
Where x is the value in decimeter.
Then we can cross multiply as :
X= (602.16 dam * 1dm)/ 0.01 dam
= 60216 decimeter.
Learn more about conversion at:
https://brainly.com/question/97386
#SPJ1
Which line plot displays a data set with an outlier?

Answers
Answer:
The 3rd one or C
Step-by-step explanation:
A B
C D
What is the place value of the 3 in the number 6,370,524,891?
Answers
ten crore is answer for India system
Step-by-step explanation:
hundred million is answer for international system
..What is 88% of 22?
Answers
Answer:
it 19.36
ynhbtgvfrdeg5t4fr
Please help meeeeeeeeeeeew
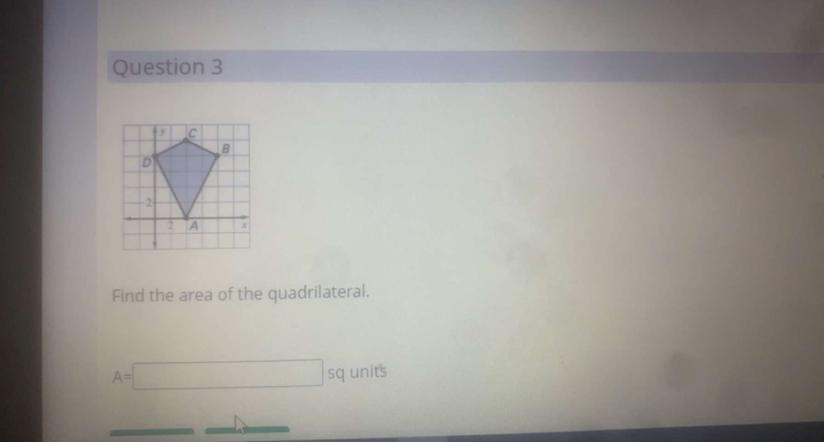
Answers
Answer:
40 sq. unitsStep-by-step explanation:
Solution 1The figure (kite) is symmetric and covers half of the area of rectangle with sides 8 units aby 10 units
The area of the rectangle:
A = 8*10 = 80 sq. unitsThe area of the kite:
A = 1/2*80 = 40 sq. unitsSolution 2Split the kite into two triangles and calculate their area and add up
Triangle DCB has b = 8, h = 2 and has area:
A = 1/2*8*2 = 8 sq. unitsTriangle DAB has b = 8, h = 8 and has area:
A = 1/2*8*8 = 32 sq. unitsTotal area:
8 + 32 = 40 sq. unitsAnswer:
Step-by-step explanation:
area=(product of diagonals)/2=(10×8)/2=40 sq. units.
what is 6 pi.
you can simplify but there's no need.
Answers
Answer:
6xpi = 18.8495559215
Step-by-step explanation:
to 2 dp 18.85
Answer:
18.8495559215
I think this is the ans
the volume of a pyramid is given by the formula V=1/, where B is the area of the base and h is the height?
Answers
Answer:
Step-by-step explanation:
The volume of this pyramid in cubic inches is 16.
Given that,
The base and height is 8 and 6.
Based on the above information, the calculation is as follows:
The volume is
= 16
Vrite an equation of the parabola in vertex form.
1. passes through (-5, 0) and has vertex
(-2, 1)
Answers
The equation of the parabola in vertex form is equal to the quadratic equation y - 1 = - (1 / 9) · (x + 2)².
How to find the equation of the parabola based on two given points
Mathematically speaking, parabolae are represented by quadratic equations, there different forms of the equation of the parabola. In this case, we must use the vertex form, whose description is shown below:
y - k = C · (x - h)²
Where:
(h, k) - Coordinates of the vertex.C - Vertex constant.If we know that (x, y) = (- 5, 0) and (h, k) = (- 2, 1), then the equation of the parabola in vertex form is:
(0 - 1) = C · (- 5 + 2)²
- 1 = 9 · C
C = - 1 / 9
y - 1 = - (1 / 9) · (x + 2)²
To learn more on parabolae: https://brainly.com/question/21685473
#SPJ1

Find the quotient of z₁ by z2. Express your answer in
trigonometric
form.
² - 3 (0 (4) + (*))
Z₁ cos
+/sin
Z₂
²2 = 7 (cos(377)+
COS
8
O A. 7 (cos (577) + i sin (5/77))
8
B.
21(cos(577)+isin (577))
8
OC. 21 cos
21(cos(-7)+ i sin(-77))
O D. 7 (cos(-7) + + sin(-7))
i
+/sin
37T
8

Answers
The quotient of z₁ by z₂ in trigonometric form is:
7/21 * (cos(584°) + i sin(584°))
To find the quotient of z₁ by z₂ in trigonometric form, we'll express both complex numbers in trigonometric form and then divide them.
Let's represent z₁ in trigonometric form as z₁ = r₁(cosθ₁ + isinθ₁), where r₁ is the magnitude of z₁ and θ₁ is the argument of z₁.
We have:
z₁ = 7(cos(577°) + i sin(577°))
Now, let's represent z₂ in trigonometric form as z₂ = r₂(cosθ₂ + isinθ₂), where r₂ is the magnitude of z₂ and θ₂ is the argument of z₂.
From the given information, we have:
z₂ = 21(cos(-7°) + i sin(-77°))
To find the quotient, we divide z₁ by z₂:
z₁ / z₂ = (r₁/r₂) * [cos(θ₁ - θ₂) + i sin(θ₁ - θ₂)]
Substituting the given values, we have:
z₁ / z₂ = (7/21) * [cos(577° - (-7°)) + i sin(577° - (-7°))]
= (7/21) * [cos(584°) + i sin(584°)]
The quotient of z₁ by z₂ in trigonometric form is:
7/21 * (cos(584°) + i sin(584°))
Option C, 21(cos(-7°) + i sin(-77°)), is not the correct answer as it does not represent the quotient of z₁ by z₂.
For more questions on trigonometric form
https://brainly.com/question/31744474
#SPJ8
By rounding to 1 significant figure, estimate
361.42 / 79.45
Answers
Answer: 5
Step-by-step explanation:
To solve this, we would have to divide 361.42 by 79.45. This will be:
= 361.42 / 79.45
= 4.549
We can see that 4.549, has 4 significant digits. By the time we round it off to 1 significant number, we would have 5.
Please help will give BRAINLIEST

Answers
Answer:
2nd table
Step-by-step explanation:
y + 3/8 = 3/4
please help
Answers
Answer:
y = 3/8
Step-by-step explanation:
Do 3/4 - 3/8 to get your answer.
3/4 - 3/8
6/8 - 3/8 = 3/8
So, y = 3/8
Answer:
3/8
Step-by-step explanation:
\(y + \frac{3}{8} = \frac{3}{4} \)
\( = > y = \frac{3}{4} - \frac{3}{8} \)
\( = > y = \frac{6 - 3}{8} \)
\( = > y = \frac{3}{8} (ans)\)
A manufacturer produces two models of toy airplanes. It takes the manufacturer 20 minutes to assemble model A and 10 minutes to package it. It takes the manufacturer 25 minutes to assemble model B and 5 minutes to package it. In a given week, the total available time for assembling is 3000 minutes, and the total available time for packaging is 1200 minutes. Model A earns a profit of $10 for each unit sold and model B earns a profit of $8 for each unit sold. Assuming the manufacturer is able to sell as many models as it makes, how many units of each model should be produced to maximize the profit for the given week?
Answers
Answer:
\(\$1320\)
Step-by-step explanation:
Let \(x\) be the number of units of A
\(y\) be the number of units of B
For assembling we have
\(20x+25y\leq 3000\)
For packaging we have
\(10x+5y\leq 1200\)
Let profits earned be \(Z\) so
\(Z=10x+8y\)
We have the maximize the function.
Plotting the equations we can see that the intersection points are \((0,120),(100,40),(120,0)\)
In the question it is mentioned we have to sell both the products so \(x\) or \(y\) cannot be \(0\).
So, the point of maximiztion for the function would be \((100,40)\)
The maximum profit would be
\(Z=10\times 100+8\times 40\\\Rightarrow Z=1320\)

What is the meaning of "\( \varphi (x,y)\) be \( y\wedge \phi (x)\) "?
![What is the meaning of "[tex] \varphi (x,y)[/tex] be [tex] y\wedge \phi (x)[/tex] "?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/IEnaK9Mnw3ftGn7VoWymvKjzqCukNTp6.png)
Answers
The given passage provides a proof that the Separation Axioms follow from the Replacement Schema.
The proof involves introducing a set F and showing that {a: e X : O(x)} is equal to F (X) for every X. Therefore, the conclusion is that the Separation Axioms can be derived from the Replacement Schema.In the given passage, the author presents a proof that demonstrates a relationship between the Separation Axioms and the Replacement Schema.
The proof involves the introduction of a set F and establishes that the set {a: e X : O(x)} is equivalent to F (X) for any given set X. This implies that the conditions of the Separation Axioms can be satisfied by applying the Replacement Schema. Essentially, the author is showing that the Replacement Schema can be used to derive or prove the Separation Axioms. By providing this proof, the passage establishes a connection between these two concepts in set theory.
Learn more about axioms here:
https://brainly.com/question/2857184
#SPJ8
Celeste is planting a rectangular flower garden in which the width will be 4 feet less than its length. She has decided to put a birdbath within the garden that will occupy a space 3feet by 4 feet how many feet are now left for planting? Express your answer on factored form
Answers
Answer:
(L-6)(L+2)
Step-by-step explanation:
Let L be the length of the flower garden.
Then the width will be L-4.
The area of the flower garden = L*(L-4) =L²-4L
The area of the birdbath is 3*4 = 12 ft²
The area of the remaining space for planting is
= Area of flower garden - area of birdbath
L² - 4L - 12We can factor the expression as follows:
L² - 4L - 12 L²-(6-2)L-12L²-6x+2x-12taking common frome each two terms
L(L-6)+2(L-6)(L-6)(L+2)Therefore, the number of feet left for planting is (L-6)(L+2) in factored form.