What is the goal of inequalities is to value what from the variable
Answers
Answer: to get the variable by itself on one side
Step-by-step explanation:
Related Questions
Use the scatter plot to fill in the missing coordinate of the ordered pair.
Eleven points in the first quadrant of a coordinate plane. The points are. Ordered pair 2 comma 18. Ordered pair 3 comma 14. Ordered pair 5 comma 16. Ordered pair 7 comma 12. Ordered pair 8 comma 17. Ordered pair 10 comma 11. Ordered pair 11 comma 7. Ordered pair 13 comma 10. Ordered pair 15 comma 4. Ordered pair 16 comma 6. Ordered pair 18 comma 3.
$\text{(}3,$
Answers
The ordered pair from the scatter plot is given as follows:
(3, 14)
What is the scatter plot?The scatter plot is built inserting all the points of the table in a graph, which are in the following input-output format:
(Input, Output).
The point (Input, Output) is called an ordered pair.
From the text in this problem, the ordered pairs of the scatter plot are given as follows:
(2,18). -> input of 2 and output of 18.(3, 14) -> missing ordered pair, with input of 3 and output of 14.(5, 16). -> input of 5 and output of 16.(7, 12). -> input of 7 and output of 12.(8, 17). -> input of 8 and output of 17.(10, 11). -> input of 10 and output of 11.(11, 7). -> input of 11 and output of 7.(13,10). -> input of 13 and output of 10.(15,4). -> input of 15 and output of 3.(16,6). -> input of 16 and output of 6.(18,3). -> input of 18 and output of 3.More can be learned about scatter plots at brainly.com/question/6592115
#SPJ1
solve for f pleaseeeee

Answers
Answer:
\(\frac{3}{5}f = 4-2m\\ f= \frac{(4-2m) X 5}{3} \\f= \frac{20-10m}{3}\)
P.S. If u want a numerical value for 'f' , now put the value of 'm'
i’ll give brainliest, just help me please : )

Answers
Rectangle Area = lw = 24(6.5)= 156
Just add them up to get 288cm squared :)
\(9x^2-4\)
please simplify!
Answers
Answer:
(3x+2)(3x−2)
Step-by-step explanation:
Write the following as an inequality.
9 is greater than x, and 2 is less than or equal to x
Use x only once in your inequality.
SOMEBODY HELP PLEASE!!!
Answers
Using the information in the diagram determine the height of the tree

Answers
Given
To find the height of the tree.
Explanation:
It is given that,
From the figure, it is clear that ΔABC and ΔADE.
That implies,
\(\begin{gathered} \frac{AD}{AB}=\frac{AE}{AC}=\frac{DE}{BC} \\ \frac{x}{2x}=\frac{y}{2y}=\frac{DE}{200} \\ \frac{1}{2}=\frac{DE}{200} \\ DE=\frac{200}{2} \\ DE=100 \end{gathered}\)Hence, the height of the tree is 100ft.


At the beginning of the month Khalid had $25 in his school cafeteria account. Use a variable to
represent the unknown quantity in each transaction below and write an equation to represent
it. Then, solve each equation. Please show ALL your work.
1. In the first week he spent $10 on lunches: How much was in his account then?
There was 15 dollars in his account
2. Khalid deposited some money in his account and his account balance was $30. How
much did he deposit?
he deposited $15
3. Then he spent $45 on lunches the next week. How much was in his account?
Answers
Let's denote the unknown quantity (amount in the account after the first week) as 'x'.
Given:
Account balance at the beginning of the month = $25
Amount spent on lunches in the first week = $10
1 - Equation: Account balance at the beginning - Amount spent = Amount in the account after the first week
x = $25 - $10
To solve the equation:
x = $15
Therefore, after the first week, there was $15 in Khalid's account.
2- Equation: Account balance after the deposit - Account balance before the deposit = Amount deposited
$30 - $15 = x
To solve the equation:
$15 = x
Therefore, Khalid deposited $15 into his account.
3- Equation: Account balance after the first transaction - Amount spent = Amount in the account after the second transaction
x = $30 - $45
To solve the equation:
x = -$15
The result is -$15, which implies that Khalid's account was overdrawn by $15 after spending $45 on lunches in the next week.
if you draw a card with a value of five or less from a standard deck of cards i will pay you 57 if not you pay me 48. what is the expected value of the bet write your answers out to two decimal places
Answers
The expected value of the bet is -15.693
According to the question we have been given that
If we draw a card with value 5 or less, we will be payed = 57
If failed to draws cards, we have to pay = 48
Now first we will find the probability of drawing cards with value less than or equal to 5.
Cards with value less than five are : 2,3,4,5
Total number of cards will be 16.
Probability = 16/52
Also number of cards with values greater than five is 36
Probability = 36/52
Thus the expected value of the bet will be
= 57*(16/52) + (-48)*(36/52) [ negative sign as we have to pay if we loose to draw the required card]
= 17.538 - 33.231
= -15.693
Hence the expected value is -15.693
learn more about probability here : https://brainly.com/question/25870256
#SPJ4
Triangle KLM, with vertices K(-6,-5), L(-5,-4), and M(-8,-2), is drawn inside a rectangle what is the area of KLM
Answers
The area of triangle KLM is 3.5 square units.
The area of triangle KLM, we first need to determine the length of its base and height.
Since the triangle is drawn inside a rectangle, we can utilize the coordinates of its vertices to calculate these values.
The base of triangle KLM is determined by the distance between points K and L.
Using the distance formula, we can find the length of KL:
KL = √[(x2 - x1)² + (y2 - y1)²]
= √[(-5 - (-6))² + (-4 - (-5))²]
= √[1² + 1²]
= √2
Next, we need to determine the height of triangle KLM.
This can be calculated by finding the perpendicular distance between the line containing KL and point M.
To do this, we use the formula for the distance between a point and a line.
The equation of the line passing through points K and L can be found by using the slope-intercept form (y = mx + b):
m = (y2 - y1) / (x2 - x1)
= (-4 - (-5)) / (-5 - (-6))
= 1/1
= 1
Using point L, we can determine the equation of the line:
-4 = 1(-5) + b
-4 = -5 + b
b = -4 + 5
b = 1
So, the equation of the line KL is y = x + 1.
Now, we can find the perpendicular distance between line KL and point M. The formula for this distance is:
Distance = |ax + by + c| / √(a² + b²)
a = 1, b = -1 (negative reciprocal of the slope), and c = -1 (substituting the coordinates of point M into the equation of line KL). Calculating the distance:
Distance = |1(-8) + (-1)(-2) + (-1)| / √(1² + (-1)²)
= |-8 + 2 - 1| / √(1 + 1)
= |-7| / √2
= 7 / √2
Now that we have the base (KL = √2) and the height (7 / √2), we can calculate the area of triangle KLM:
Area = (1/2) × base × height
= (1/2) × √2 × (7 / √2)
= (1/2) × 7
= 7/2
= 3.5
For similar questions on area of triangle
https://brainly.com/question/17335144
#SPJ11
What percentage of the global oceans are Marine Protected Areas
(MPA's) ?
a. 3.7% b. 15.2% c. 26.7% d. 90%
Answers
Option (c) 26.7% of the global oceans are Marine Protected Areas (MPAs). Marine Protected Areas (MPAs) are designated areas in the oceans that are set aside for conservation and management purposes.
They are intended to protect and preserve marine ecosystems, biodiversity, and various species. MPAs can have different levels of restrictions and regulations, depending on their specific objectives and conservation goals.
As of the current knowledge cutoff in September 2021, approximately 26.7% of the global oceans are designated as Marine Protected Areas. This means that a significant portion of the world's oceans has some form of protection and management in place to safeguard marine life and habitats. The establishment and expansion of MPAs have been driven by international agreements and initiatives, as well as national efforts by individual countries to conserve marine resources and promote sustainable practices.
It is worth noting that the percentage of MPAs in the global oceans may change over time as new areas are designated or existing MPAs are expanded. Therefore, it is important to refer to the most up-to-date data and reports from reputable sources to get the most accurate and current information on the extent of Marine Protected Areas worldwide.
Learn more about percentage here: brainly.com/question/29541337
#SPJ11
How do you find the general solution of an exact differential equation?
Answers
The general solution of an exact differential equation can also be found by solving the associated homogenous equation and adding the particular solution obtained from the original equation.
1. Identify the exact differential equation.
2. Find the integrating factor by multiplying the equation by an expression of the form e^(f(x)).
3. Multiply the integrating factor with the equation to make it exact.
4. Integrate both sides of the equation to obtain the general solution.
5. Check the solution by differentiating it to confirm that it satisfies the original equation.
6. Add the particular solution obtained from the original equation to the homogenous solution to get the general solution.
The general solution of an exact differential equation can be found by using an integrating factor. An integrating factor is a function of the independent variable which can be multiplied with the equation in order to make it exact. Once the equation has been made exact, it can be solved using the standard integration techniques. In addition, the general solution can be found by solving the associated homogenous equation and then adding the particular solution obtained from the original equation.
Learn more about equation here
https://brainly.com/question/29657992
#SPJ4
Peter wants to buy a coat that costs $87 at full price.The coat is now on sale for 40% off
Part A: Explain how Peter can use the fact that 10% of $87 is $8.70 to find the amount he will save on the coat
Part B: Use the same method to find the amount Peter would save on a $64 coat that is on sale for 40% off
Answers
Step-by-step explanation:
Hello!
Part A
Peter can use the fact that 10% of 87 is 8.70 to find the amount he would save because 40% is just 4 times bigger than 10% so he can take 8.70 from to total of the coat 4 times to find out how much it cost.
Part B
Using the same method we know that 10% of 64 is 6.40 so we subtract that from the price of the coat 4 times to find out how much it cost
64 - 6.40 = 57.6
57.6 - 6.40 = 51.2
51.2 - 6.40 = 44.8
44.8 - 6.40 - 38.4
The price of the coat is $38.4
Hope this helps!
Suppose a city with population 300,000 has been growing at a rate of 2% per year. If this rate continues, find the population of this city in 20 years
I need help solving this
Answers
6000x20=120,000
The answer is 120,000
Answer:
the answer is 445,784
Step-by-step explanation:
The population y after x years of growth with the growth rate r and the original population C can be found using the exponential growth formula, . Substitute the decimal equivalent for the percent growth rate per year for r.
A student in the Construction Trades program at the Cecil County School of Technology has 4 1/2gallons of paint. If he uses 2.75 gallons of the paint in one room, how many gallons of paint are left? Show your work on your paper and write your final equation and correct answer in the box below.
Answers
Answer:
1.75 gallons of paint
Step-by-step explanation:
A student in the construction trades program has 4 1/2 gallons of paint
If the student uses 2.75 gallons in one room then the gallons of paint that are left can be calculated as follows
= 4 1/2 - 2.75
= 9/2 - 2.75
= 4.5 - 2.75
= 1.75
Hence 1.75 gallons of paint are left
The variables a, b, and c represent polynomials where a = x2, b = 3x 2, and c = x – 3. what is ab – c2 in simplest form? 3x3 2x2 – x 3 3x3 2x2 – x – 3 3x3 x2 – 6x 9 3x3 x2 6x – 9
Answers
The simplest form of a^2-ab is given by 3x^3 + x^2 + 6x - 9.
We have given that,
a = x^2,
b = 3x + 2,
c = x – 3
We have to determine ab- c^2.
What is the meaning of the simplest form?
A fraction is in its simplest form when the numerator and the denominator have no common factors besides one.
ab- c^2
\(=x^2(3x+2) - (x-3)^2\\ =3x^3 + 2x^2 - (x^2 - 6x + 9) \\=3x^3 + 2x^2 - x^2 + 6x - 9 \\=3x^3 + x^2 + 6x - 9\\\)
The simplest form of a^2-ab is given by 3x^3 + x^2 + 6x - 9.
To learn more about the simplest form visit:
https://brainly.com/question/29114
please help asap!!!!

Answers
Answer:
y = 3 + the square root of 2.
Step-by-step explanation:
message me if you have any other math questions
=3±2√
hopes this helps!! ^^
Keiko tosses one penny and Ephraim tosses two pennies. The probability Ephraim gets the same number of heads that Keiko gets is
(A)1/4
(B)3/8
(C)1/2
(D)2/3
(E)3/4
Answers
The probability that Ephraim gets the same number of heads that Keiko gets is (A)1/4.
What is the probability?Probability refers to a possibility that deals with the occurrence of random events.
The probability of all the events occurring need to be 1.
The formula of probability is defined as the ratio of a number of favorable outcomes to the total number of outcomes.
Given that Keiko tosses one penny and Ephraim tosses two pennies.
We need to find the probability Ephraim gets the same number of heads that Keiko gets;
Probability = 1/4 chance for Ephraim
Probability = 1/2 chance for Keiko
Hence, the probability that Ephraim gets the same number of heads that Keiko gets is (A)1/4.
Learn more about probability here;
https://brainly.com/question/9326835
#SPJ1
Solve for x. (Geometry)

Answers
Answer:
x = 7
Step-by-step explanation:
The indicated angles are vertical and congruent, thus
14x + 2 = 13x + 9 ( subtract 13x from both sides )
x + 2 = 9 ( subtract 2 from both sides )
x = 7
HOPE THIS IS THEANSWER YOU NEEDED
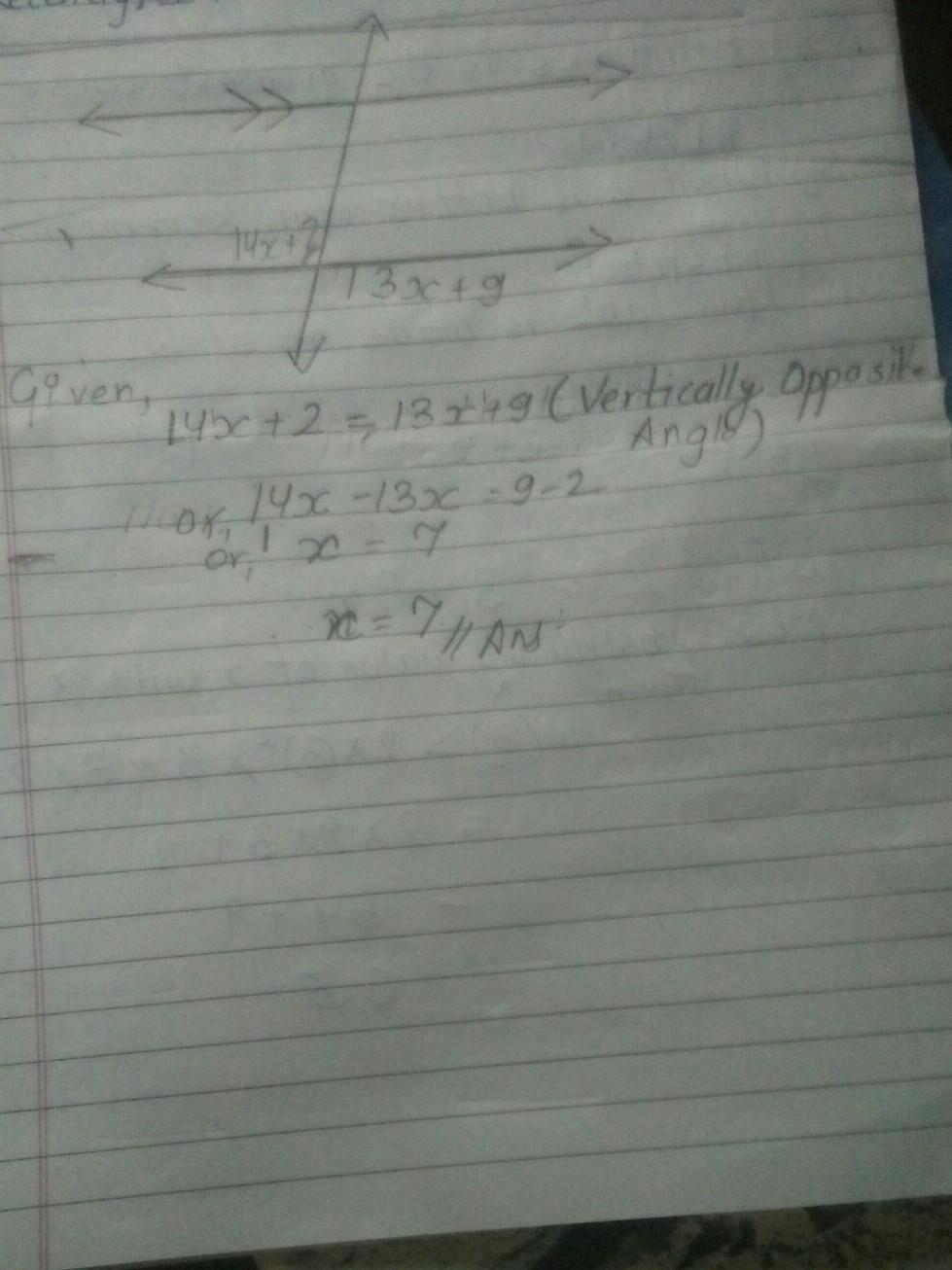
Someone pls help... On November 1st there were 2500 boxes in a warehouse. On December 1st there were 15% fewer boxes in the warehouse than there were on November 1st. On January 1st there were 20% more boxes in the warehouse than there were on December 1st. How many boxes were in the warehouse on January 1st.
Answers
Answer:
Nov 1st: 2500 boxes
Dec 1st: 15% fewer boxes which is 2500 x (1- \(\frac{15}{100}\) ) = 2125
On January 1st: 20% more boxes which is 2125 x (1+ \(\frac{20}{100}\) ) = 2550 is the number of boxes
Step-by-step explanation:
If the measures of two opposite angles of an isosceles trapezoids are 2x + 20 and 3x, what is the value of x?
Answers
Answer:
x = 32
Step-by-step explanation:
An isosceles trapezium is one in which non-parallel sides have equal measure.
For an isosceles trapezoid, it is a rule that the two opposite angles equal 180°
∴ 2x + 20 3x = 180
solving the above equation:
2x + 3x = 180 - 20
5x = 160
x = 160 ÷ 5
x = 32
A crafts worker is knitting a circular rug that has a diameter of 88 inches. He would like to put trim around the outer edge of the rug. If 1 inch = 2.54 centimeters, how many centimeters of trim would he need? Use π = 3.14 and round to the nearest centimeter.
208 centimeters
257 centimeters
276 centimeters
702 centimeters
Answers
Answer: 702 cm
Step-by-step explanation:
We must first find the circumference of the circle using the circumference formula of
c=πd , or c=π2r
Substitute the given values into the formula
c=88π , or c=88*3.14
c=276.32
The circumference is 276.32 inches, but we need that measurement in centimeters.
In order to convert the inches to centimeters, we can multiply our circumference by the inch/centimeter scalar , 2.54 .
276.32 * 2.54
= 702 (rounded)
assuming that the p-value to test that the population mean number of errors for the ethanol group (e) is greater than the population mean number of errors for the placebo group (p) is 0.0106 and using a 1% significance level, what is the best conclusion from this hypothesis test in the context of the problem?
Answers
The best conclusion from this hypothesis test in the context of the problem is that we can reject the null hypothesis. The null hypothesis for this problem is that the errors is not greater than the population mean.
What is the best conclusion?The null hypothesis for this problem is that the population mean number of errors for the ethanol group is not greater than the population mean number of errors for the placebo group.
In other words, the null hypothesis is: H₀: μe ≤ μp. The alternative hypothesis is that the population mean number of errors for the ethanol group is greater than the population mean number of errors for the placebo group. In other words, the alternative hypothesis is: H₁: μe > μp.
The p-value is the probability of getting a test statistic at least as extreme as the one observed, assuming the null hypothesis is true. In this case, the p-value is 0.0106, which is less than the significance level of 0.01. This means that the observed test statistic is significant at the 1% level, and we reject the null hypothesis.
Therefore, we conclude that there is evidence to suggest that the population mean number of errors for the ethanol group is greater than the population mean number of errors for the placebo group.
Learn more about Hypothesis here:
https://brainly.com/question/29519577
#SPJ11
Square has side length 2. the diagonal is approximately how long?
Answers
Pls help i need help on this homework equation m% of n will mark brainliest
Answers
Answer:
m% of n is (m/100)(n)
Step-by-step explanation:
When removing a %, you just move the period two places to the left (ex. 50% = 0.50), or just divide the number by a 100 (ex. 50% = 50/100). So then, m% of n is just the product of m/100 and n.
Suppose that y varies directly with x , and y=21 when x=3. write a direct variation squation that relates x and y. then find y when x=-2
Answers
\(\qquad \qquad \textit{direct proportional variation} \\\\ \textit{\underline{y} varies directly with \underline{x}}\qquad \qquad \stackrel{\textit{constant of variation}}{y=\stackrel{\downarrow }{k}x~\hfill } \\\\ \textit{\underline{x} varies directly with }\underline{z^5}\qquad \qquad \stackrel{\textit{constant of variation}}{x=\stackrel{\downarrow }{k}z^5~\hfill } \\\\[-0.35em] ~\dotfill\)
\(\stackrel{\textit{"y" varies directly with "x"}}{y = k(x)}\hspace{5em}\textit{we also know that} \begin{cases} y=21\\ x=3 \end{cases} \\\\\\ 21=k(3)\implies \cfrac{21}{3}=k\implies 7=k\hspace{5em}\boxed{y=7x} \\\\\\ \textit{when x = -2, what is "y"?}\qquad y=7(-2)\implies y=-14\)
A= (a, b}
B = {1,2,3}
Select the expression that is an element of AxBxB.
a. (1,2,3)
b. (a, a,1)
c. (b,2^2)
d. (2.1.1)
Answers
The expression that is an element of AxBxB is (1,2,3)
The given data is A= (a, b}, B = {1,2,3}
The product of two matrices A and B is defined if the number of columns of A is equal to the number of rows of B. If both A and B are square matrices of the same order, then both AB and BA are defined.
\(& \ A \times B=\left\{\begin{array}{c}(a, 1),(a, 2),(a, 3),(b, 1) \\(b, 2),(b, 3)\end{array}\right. \\\)
\(& A \times B \times B=\left\{\begin{array}{l}(a, 1,1),(a, 1,2),(a, 1,3), \\(a, 2,1),(a, 2,2),(a, 2,3),\end{array}\right. \\& (a, 3,1),(a, 3,2),(a, 3,3) \\ & (b, 1,1),(b, 1,2),(b, 1,3) \\& \left.\begin{array}{l}(b, 2,1),(b, 2,2),(b, 2,3) \\(b, 3,1),(b, 2),(b, 3,3)\end{array}\right\} \\\)
\(& \therefore(b, 2,3) \in D \times B \times B \\\\& (a, a, 1) \notin A \times B \times B \\\\& \left(b, 2^2\right) \quad \forall A \times B \times B \\\\& (2,1,1) \notin A \times B \times B \\\\&=(b, 2,3) \in \cap \times B \times B \\&\end{aligned}\)
The union of two sets X and Y is equal to the set of elements that are present in set X, in set Y, or in both the sets X and Y.
The intersection of sets can be denoted using the symbol ‘∩’. As defined above, the intersection of two sets A and B is the set of all those elements which are common to both A and B. Symbolically, we can represent the intersection of A and B as A ∩ B.
Therefore, the expression that is an element of AxBxB is (1,2,3).
For more such questions on sets
https://brainly.com/question/28492445
#SPJ4
Factor the polynomial x^2 + 4x + 4
Answers
Quadrilateral MNOP with verticles M(3,-1), N(8,-4), (6,-6), and P(1,-7); is rotated 180 degrees. What are the new points?
Answers
Answer:
The new points after a rotation of 180 degrees is;
M’ = (-3, 1)
N’ = (-8,4)
O’ = (-6,6)
P’ = (-1 , 7)
Step-by-step explanation:
Given a point (x , y) and we rotate by 180 degrees , the new point will be (-x , -y)
So to the question;
M’ = (-3, 1)
N’ = (-8,4)
O’ = (-6,6)
P’ = (-1 , 7)
What is the probability that the component is not working given that the system works? (enter your answer with 3 decimal digits.)
Answers
The value of P((A ∩ B) ∪ (C ∪ D ∩ E))' is approximately 0.1571. the probability that component A is not working given that the system works is approximately 0.001.
To calculate the values in Part 1 and Part 2, we'll use basic probability rules and formulas.
Given: P(A) = P(B) = 0.77, P(C) = P(D) = P(E) = 0.85
Part 1: We want to find the probability of the complement of the event (A ∩ B) ∪ (C ∪ D ∩ E), denoted as P((A ∩ B) ∪ (C ∪ D ∩ E))'.
Using De Morgan's law, the complement of a union is the intersection of complements:
P((A ∩ B) ∪ (C ∪ D ∩ E))' = P((A ∩ B)') ∩ (C ∪ D ∩ E)'
The complement of an intersection is the union of complements:
P((A ∩ B)') ∩ (C ∪ D ∩ E)' = (P(A') ∪ P(B')) ∩ (P(C') ∩ P(D') ∩ P(E'))
Substituting the given probabilities:
P((A ∩ B)') ∩ (C ∪ D ∩ E)' = (1 - P(A)) ∪ (1 - P(B)) ∩ (1 - P(C)) ∩ (1 - P(D)) ∩ (1 - P(E))
Calculating the values:
P(A') = 1 - P(A) = 1 - 0.77 = 0.23
P(B') = 1 - P(B) = 1 - 0.77 = 0.23
P(C') = 1 - P(C) = 1 - 0.85 = 0.15
P(D') = 1 - P(D) = 1 - 0.85 = 0.15
P(E') = 1 - P(E) = 1 - 0.85 = 0.15
Now, we calculate the final probability:
P((A ∩ B)') ∩ (C ∪ D ∩ E)' = (0.23 ∪ 0.23) ∩ (0.15 ∩ 0.15 ∩ 0.15)
= 0.23 ∩ 0.15 = 0.1571 (rounded to 4 decimal places)
Therefore, the value of P((A ∩ B) ∪ (C ∪ D ∩ E))' is approximately 0.1571.
Part 2: We want to find the probability that component A is not working given that the system works, denoted as P(A' | System Works).
Using the conditional probability formula:
P(A' | System Works) = P(A' ∩ System Works) / P(System Works)
To calculate the numerator:
P(A' ∩ System Works) = P(A' ∩ B' ∩ C' ∩ D' ∩ E')
= P(A') ∩ P(B') ∩ P(C') ∩ P(D') ∩ P(E')
= 0.23 ∩ 0.23 ∩ 0.15 ∩ 0.15 ∩ 0.15 = 0.0002634 (rounded to 7 decimal places)
To calculate the denominator:
P(System Works) = 1 - P(A' ∪ B' ∪ C' ∪ D' ∪ E')
= 1 - (P(A') ∪ P(B') ∪ P(C') ∪ P(D') ∪ P(E')) = 1 - (0.23 ∪ 0.23 ∪ 0.15 ∪ 0.15 ∪ 0.15) = 1 - 0.66 = 0.34
Now, we calculate the final probability:
P(A' | System Works) = P(A' ∩ System Works) / P(System Works)
= 0.0002634 / 0.34 = 0.0007735 (rounded to 7 decimal places)
Therefore, the probability that component A is not working given that the system works is approximately 0.001.
To learn more about probability visit:
brainly.com/question/23417919
#SPJ11
The complete question is:<The reliability (probability of working) of each component is specified as follows and the components work or fail independently. P(A) = P(B) = 0.77 P(C) = P(D) = P(E) = 0.85 A B с DHE Part 1 What is the value of P((ANB) U(CODn E))' (Enter your answer with 3 decimal digits.) 0.1571 100% Part 2 What is the probability that the component A is not working given that the system works? (Enter your answer with 3 decimal digits.) Hint: Think of a conditional probability definition.>
A fast food restaurant just leased a new freezer and food fryer for three years. The service contract for the freezer offers unlimited repairs for a fee of $125 a year plus a $35 service charge for each repair needed. The restaurant’s research indicates that during a given year 80% of these freezers need no repairs, 11% needed to be serviced once, 5% twice, 4% three times, and none required more than three repairs.
a. Find the expected number of repairs for this freezer per year.
b. Find the standard deviation of the number of repairs per year.
c. What are the mean and standard deviation of the restaurant’s annual expense with the service contract for the freezer?
Answers
(a) Expected number of repairs per year is 0.33 (b) Standard deviation of number of repairs per year is 0.749, (c) The mean and standard deviation of annual expense are $136.55 and $26.217 respectively.
What is Standard Deviation?Standard deviation is a measure in statistics which measures the amount of deviation a set of data has with respect to their mean.
(a) Expected number of repairs for the freezer per year is the sum of the product of number of repairs to their probability.
E(Repairs) = (0 × 0.80) + (1 × 0.11) + (2 × 0.05) + (3 × 0.04)
= 0.33
(b) Standard deviation of number of repairs per year can be calculated as,
SD(Repairs) = \(\sqrt{[(0 - 0.33)^{2}(0.8)]+[(1-0.33)^{2}(0.11)] + [(2-0.33)^{2}(0.05)]+[(3-0.33)^{2}(0.04)] }\)
= √ (0.5611)
= 0.749
(c) Mean of the restaurant's annual expense with service contract is,
Mean = Expected cost = $125 + ($35 × 0.33) = $136.55
Standard deviation of the restaurant's annual expense with service contract is,
SD = \(\sqrt{35^{2}(0.5611) }\) = 35 × 0.759 = 26.217
Hence the expected number of repairs is 0.33, standard deviation of number of repairs is 0.749, mean and standard deviation of annual expense is $136.55 and $26.217 respectively.
Learn more about Standard Deviation here :
https://brainly.com/question/23907081
#SPJ1