what is the equivalent to 18/18?
Answers
Answer:
1
Step-by-step explanation:
Related Questions
Which equation shows y=3x−15 in standard form? 5x−15y=−1 5x−15y=1 15x+5y=−1 15x−5y=1
Answers
Answer:
3x-y=15 should be the answer
Find the length of DB

Answers
Answer:
4
Step-by-step explanation:
this line is congruent to EC on the base
I would appreciate help without guessing :)

Answers
Answer:
a) \(\sqrt{56\) → Definitely not undefined because 56 is a positive real number
b) \(-\sqrt{56\) → Definitely not undefined because 56 is a positive real number (and the negative sign is not under the square root)
c) \(\sqrt{-56\) → Definitely undefined because -56 is a negative number
__
We know that there is no real square root of a negative number because nothing multiplied by itself results in a negative number.
__
d) \(\sqrt h\) → Could be undefined because we don't know the value of \(h\); it could be positive or negative
e) \(-\sqrt {h\) → Could be undefined because we don't know the value of \(h\); it could be positive or negative (and the negative sign doesn't affect this because it is outside the square root)
f) \(\sqrt{-h\) (when \(h\) is positive) → Definitely undefined because the value inside of the square root is negative (a negative times a positive is a negative)
Which angle has sides DB and DC? Select all that apply.
Answers
No, rectangle DABC is not the result of a dilation of rectangle HEFG with a center of dilation at the origin.
What is dilation?Dilation is a geometrical transformation that changes the size of a shape or figure. It is one of the four basic transformations of geometry alongside translation, rotation, and reflection. Dilation involves resizing a shape by a scale factor and keeping its overall shape intact. The scale factor is the ratio of the size of the image to the size of the original figure.
Dilation involves a scaling of a shape, where each point on the shape is moved away from or closer to the center of dilation, proportional to its distance from the center. In this case, the angles of rectangle DABC are different from the angles of rectangle HEFG, so it is not the result of a dilation. The angles of rectangle HEFG are ∠2, ∠33, ∠EDC, whereas the angles of rectangle DABC are ∠ADB, ∠BDC, and ∠CDB.
To learn more about dilation
https://brainly.com/question/26855848
#SPJ1
Before recess, Marcy has math class for 1 hour and 50 minutes. Recess lasts for 30 minutes and ends at 11:55 A.M. What time does her math class start?
Answers
Answer:
Marcy's math class starts at 9:35.
Step-by-step explanation:
11:55
-50 = 11:05 This gets rid of 50 minutes of math class.
11:05
-30 = 10:35 This gets rid of the 30 minutes of recess.
Now subtract one more hour to subtract the remainder of math class, and you get 9:35. Marcy's math class starts at 9:35.
Can you use the lengths of the hypotenuse and a leg to show right triangles are congruent?
Answers
In other words, the triangles are consistent if the hypotenuse and one of the legs of one right triangle agree with the hypotenuse and one of the legs of another right triangle.
What is meant by congruent triangles?Congruent triangles are two triangles that are the same size and shape. Two congruent triangles remain congruent even if we flip, turn, or rotate one of them. Two triangles must have the same angles and, as a result, must be congruent if their sides are the same.
Two right triangles are supposed to be consistent on the off chance that they are of a similar shape and size. All in all, two right triangles are supposed to be consistent in the event that the proportion of the length of their comparing sides and their relating points is equivalent.
Right triangles are harmonious in the event that both the hypotenuse and one leg are a similar length. These triangles are harmonious by HL or hypotenuse leg.
To learn more about congruent triangles refer to:
https://brainly.com/question/2938476
#SPJ4
The back to back stem plot shows the number of books read in a year by a group of high school and college students which statements are correct?

Answers
The correct statement are:
The range for high school students is larger than college students.The college median is equal to the high school median.Based on the given information, we can make the following conclusions:
A. The interquartile range for high school students is smaller than college students.
The statement is False
B. The mean for high school students is smaller than college students.
The statement is False because the mean of College is 25.28 and mean for High school is 30.4.
C. The range for high school students is larger than college students.
The statement is True .
D. The college median is equal to the high school median.
The statement is True because the median for both is 24..
E. The mean absolute deviation is larger for college students than high school students.
The statement is False.
Learn more about plot here:
https://brainly.com/question/32275669
#SPJ1
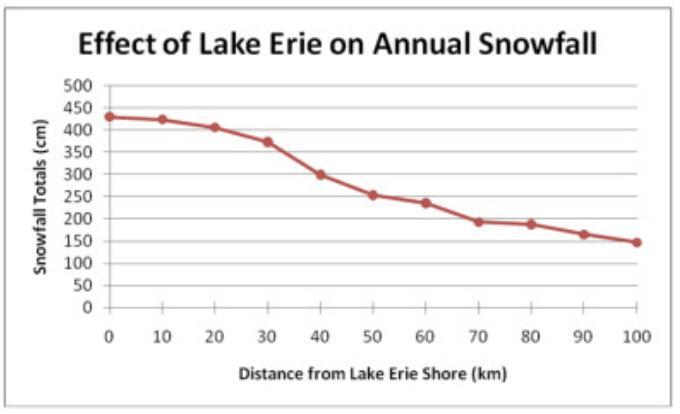
lake erie line graph text-based description: line graph showing declining snowfall totals with distance from the shore of lake erie. the gradual decline from around 425 cm to 375 cm between 0 and 30 km increases with total snowfall at 250 cm by 50 km. there is little decline in the following 10 km but it does drop again by around 50 cm over the next 10 km. the remaining decline is relatively consistent out to 100km, with snowfall there at 150 cm. what is the spatial scale at which the data was collected?
Answers
The spatial scale at which the data was collected is the distance from the shore of Lake Erie.
We can see that the data shows a gradual decline in snowfall totals with increasing distance from the shore of Lake Erie. The decline starts at around 425 cm at 0 km and decreases to 375 cm by 30 km. It then decreases more quickly over the next 20 km before declining relatively consistently out to 100 km, where the snowfall is 150 cm.
The graph shows the declining snowfall totals with increasing distance from the shore of Lake Erie, starting from 0 km and ending at 100 km. The data points are measured in increments of 10 km, with the total snowfall measured in cm.
To know more about spatial scale, here
https://brainly.com/question/14781354
#SPJ4
Solve each quadratic equation by factoring
X+3=24x
Answers
Answer = X= 3/23
Given: rt || sp, rq ≅ qp, rp bisects st at q prove: δrqt ≅ δpqs triangles r q t and p q s are connected at point q. lines r t and s p are parallel. the lengths of lines r q and q p are congruent. tamir is working to prove the triangles congruent using sas. after stating the given information, he states that tq ≅ qs by the definition of segment bisector. now he wants to state that ∠rqt ≅ ∠pqs. which reason should he use? alternate interior angles theorem corresponding angles theorem linear pair postulate vertical angles theorem
Answers
Answer:
(d) vertical angles theorem
Step-by-step explanation:
Vertical angles have a common vertex and are formed from opposite rays.
__
Angles RQT and PQS share vertex Q, Rays QR and QP are opposite, creating line RP. Rays QT and QS are opposite, creating line ST. Hence angles RQT and PQS are vertical angles. The vertical angles theorem says those angles are congruent.
Use the Line Tool to graph the equation. 3x−y=9
Answers
Answer:
Step-by-step explanation:
Solve for
y
y
.
Tap for more steps...
y
=
−
9
+
3
x
y
=
-
9
+
3
x
Rewrite in slope-intercept form.
Tap for more steps...
y
=
3
x
−
9
y
=
3
x
-
9
Use the slope-intercept form to find the slope and y-intercept.
Tap for more steps...
Slope:
3
3
y-intercept:
−
9
-
9
Any line can be graphed using two points. Select two
x
x
values, and plug them into the equation to find the corresponding
y
y
values.
Tap for more steps...
x
y
2
−
3
3
0
x y 2 -3 3 0
Graph the line using the slope and the y-intercept, or the points.
Slope:
3
3
y-intercept:
−
9
-
9
x
y
2
−
3
3
0
x y 2 -3 3 0
image of graph
The circumference of the hub cap of a tire is 73.04 centimeters. Find the area of this hub cap. Use 3.14 for π. Use a pencil and paper. If the circumference of the hub cap were smaller, explain how this would change the area of the hub cap.
Answers
C = 2πr
where C is the circumference, π is the constant pi, and r is the radius of the circle. We can rearrange this formula to solve for the radius:
r = C / 2π
Plugging in the given circumference of 73.04 centimeters, and using 3.14 for π, we get:
r = 73.04 cm / (2 x 3.14)
r = 11.62 cm
Now that we know the radius, we can use the formula for the area of a circle:
A = πr^2
Plugging in the radius we just found, we get:
A = 3.14 x (11.62 cm)^2
A = 424.5 cm^2
Therefore, the area of the hub cap is 424.5 square centimeters.
If the circumference of the hub cap were smaller, this would mean that the radius of the hub cap would be smaller as well. This would result in a smaller area for the hub cap, since the area of a circle is proportional to the square of its radius. So a smaller circumference would mean a smaller area for the hub cap.
please help with the following two questions :)

Answers
Answer:
10) -1.5
11) 1
Step-by-step explanation:
Hope this helps! Pls give brainliest!
In a certain chemical, the ratio of zinc to copper is 3 to 14 . A jar of the chemical contains 574 grams of copper. How many grams of zinc does it contain? NEED THIS ASAP
Answers
=============================================
Work Shown:
(zinc)/(copper) = 3/14
(x grams of zinc)/(574 grams of copper) = 3/14
x/574 = 3/14
14x = 574*3
x = 574*3/14
x = 123 grams of zinc
A card is drawn at random from a standard deck of cards. Find the probability of drawing:
1. A queen or a spade.
II. A black or a face card.
III. A red queen.
Answers
Given that a card is drawn at random from a standard deck of cards. We are asked to find the probabilities of
1) A queen or a spade.
2) A black or a face card.
3) A red queen.
This can be seen below;
Explanation
The formula for the probability of an event is given as;
\(\text{Pr(event) =}\frac{\text{number of events}}{\text{number of total possible outcomes}}\)For a given deck of cards, the number of total possible outcomes is 52 different cards. Next, we find the number of events for each case
\(\begin{gathered} n(\text{queen)}=4 \\ n(\text{spades)}=13 \\ n(\text{black)}=26 \\ n(\text{face card)=}12 \\ n(\text{red queen) =2} \end{gathered}\)Therefore we can find the probability in each case. Recall that "or" in probability implies we will add the values of the probabilities we are comparing.
1) A queen or a spade
\(Pr(\text{queen or spade)= }\frac{4}{52}+\frac{13}{52}=\frac{17}{52}\)Answer
\(Pr(\text{queen or spade)=}\frac{17}{52}\)
2) A black or a face card
\(Pr(black\text{ or }facecard)=\frac{26}{52}+\frac{12}{52}=\frac{38}{52}=\frac{19}{26}\)
Answer:
\(Pr(\text{black or facecard)=}\frac{\text{19}}{26}\)3) A red queen
\(Pr(A\text{ }red\text{ }queen)=\frac{2}{52}=\frac{1}{26}\)
Answer
\(Pr(A\text{ }red\text{ }queen)=\frac{1}{26}\)
SOMEONE HELP ME!! NO ONE WILL HELP T^T WILL MARK BRAINLIEST

Answers
Answer: nope!
Step-by-step explanation: there are 4 quarts in a gallon and we can see by adding the mango juice, there will be no space!
Water (2 quarts) mango juice (2 quarts) equals a gallon
Ginger ale = one gallon
That’s already 2 gallons and we still have the 2 pints of pineapple juice!
Can you explain to me how to solve this?????
√19x^5
Answers
The final step when solving the given math problem is:
Take the fifth root of both sides: x = \(((y^2)/19)^(^1^/^5)\)
How to solveTo solve √19x^5 for x, follow these steps:
Isolate the square root term: \(\sqrt{19x^5}\) = y (Let y be the other side of the equation)
Square both sides: \((y^2) = 19x^5\)
Divide both sides by 19: \((y^2)/19 = x^5\)
Take the fifth root of both sides: x = \(((y^2)/19)^(^1^/^5^)\)
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the symbol √ and can be found using mathematical operations.
Read more about square roots here:
https://brainly.com/question/428672
#SPJ1
Look at the picture please (IM GIVING OUT 50 POINTS TO WHOEVER ANSWER THIS CORRECTLY AND I WILL MARK BARINLIEST)
3. Use your graph to answer the following questions
3a. If King sets the price at $2.50 per doll how many disappointing customers will each store have during the week?
3b. If King sets the price at $3.80 per doll how many unsold dolls will remain at each store at the end of the week?
3c. According to this graph, if the company could give the dolls away, how many would each door need per week?
3d. According to this graph, what price would make the doll supply so tight that the average number available to each store would be zero?
3e. Estimate the price where supply and demand will be in equilibrium
4. Complete the following using equations.
A. Use two of the points, giving to find the equation for supply (S) as a function of price (P)
B. Use two of the points given to find the equation for demand (D) as a function of price (P)
C solve the system of supply and demand equations to find the price in exact equilibrium. How does this price compare with your answer in question 4e above?

Answers
a. The number of disappointed customers is 157. b. Unsold dolls = 135. c. The dolls needed per week is 660. d. The price of $0.63 will make the supply of the doll tight. e. The price at which the demand and supply will be at equilibrium is $3.20.
What are functions?A mathematical phrase, rule, or law that establishes the link between an independent variable and a dependent variable (the dependent variable). In mathematics, functions exist everywhere, and they are crucial for constructing physical links in the sciences.
a. The supply and the demand associated from the graphs are:
Supply: 95(2.50) - 60 = 178
Demand: -130(2.50) + 660 = 335
Subtracting the Demand and supply:
335 - 178 = 157
The number of disappointed customers is 157.
b. For unsold dolls set the equation for supply and demand:
Supply: 95(3.80) - 60 = 301
Demand: -130(3.80) + 660 = 166
Subtract the value of demand and supply:
301 - 166 = 135
Unsold dolls = 135
c. To give the dolls away, the cost of the doll is $0.
The demand equation thus becomes:
y = -130(0) + 660
y = 660
The dolls needed per week is 660.
d. Let the supply be 0.
y = 95x - 60
0 = 95x -60
x = $0.63
The price of $0.63 will make the supply of the doll tight.
e. The supply an demand will be in equilibrium when Demand = Supply, that is:
95x - 60 = -130x + 660
95x + 130x = 720
225x = 720
x = $3.20
The price at which the demand and supply will be at equilibrium is $3.20.
Learn more about functions here:
https://brainly.com/question/12431044
#SPJ1
need this asap please

Answers
Answer:
temperature ≤ 6
Step-by-step explanation:
The highest temperature in February was 6°F. Write and graph an inequality to represent this situtation.
If the maximum temperature was 6, then the temperature reached no more than six, while still reaching 6. Thus, the inequality should be
temperature ≤ 6
The graph would be a filled dot on the 6 pointing towards the left side of the graph (towards the -10 side)
B
_ + 2 = -1
4
What is the value of B?
Answers
\( \frac{b}{4} + 2 = - 1\)
\( \frac{b}{4} = - 1 - 2 = - 3\)
\(b = - 3 \times 4 = - 12\)
Answer: -12
ok done. Thank to me :>
(Chapter 12) The vector <3, -1, 2> is parallel to the plane 6x-2y +4z = 1
Answers
The vector is parallel to the plane the vector <3, -1, 2> is not orthogonal to the normal vector of the plane 6x - 2y + 4z = 1
To determine if the vector <3, -1, 2> is parallel to the plane 6x - 2y + 4z = 1, we need to check if the vector is orthogonal (perpendicular) to the normal vector of the plane.
Find the normal vector of the plane.
The normal vector of a plane is given by the coefficients of x, y, and z in the equation of the plane. In this case, the normal vector is <6, -2, 4>.
Check if the given vector is orthogonal to the normal vector.
Two vectors are orthogonal if their dot product is equal to 0. Let's compute the dot product between the given vector <3, -1, 2> and the normal vector <6, -2, 4>:
Dot product = (3 * 6) + (-1 * -2) + (2 * 4) = 18 + 2 + 8 = 28
Since the dot product is not equal to 0 (28 ≠ 0), the given vector <3, -1, 2> is not orthogonal to the normal vector of the plane.
The vector <3, -1, 2> is not orthogonal to the normal vector of the plane 6x - 2y + 4z = 1, which means it is parallel to the plane.
More on vectors: https://brainly.com/question/31140426
#SPJ11
the individual values contained in an array are known as
Answers
The individual values contained in an array are known as elements.
An array is a data structure that allows you to store multiple values of the same data type in a single variable. Each value within the array is assigned a unique index or position, starting from 0 for the first element. These elements can be accessed and manipulated using their respective indices.
By organizing related data into an array, it becomes easier to perform operations on the entire set of values or access specific elements based on their positions. Elements in an array can be of any data type, such as numbers, characters, or objects, depending on the programming language used.
To know more about elements:
https://brainly.com/question/13391088
#SPJ4
(1 point) Solve the following differential equation by variation of parameters. Fully evaluate all integrals. y" 4y sec(2z). a. Find the most general solution to the associated homogeneous differential equation. Use c and c2 in your answer to denote arbitrary constants, and enter them as c1 and c2 b. Find a particular solution to the nonhomogeneous differential equation y" +4y sec(2). c. Find the most general solution to the original nonhomogeneous differential equation. Use ci and c2 in your answer to denote arbitrary constants.
Answers
The general solution of equation y''+4y=sec(2z) is
y = c₁cos2z + c₂sin2z + \(\frac{cos2z}{4}\) ln(cos2z) + \(\frac{z sin2z}{2}\).
Given differential equation is,
y'' + 4y = sec(2z)
Characteristic equation of this equation is
(D²+4)=0
⇒ D² = -4
D = ±2i
Therefore the roots are imaginary.
D₁=2i ⇒ y₁ = e⁰cos2z = cos2z
D₂=-2I⇒ y₂ = e⁰sin2z = sin2z
yn= c₁cos2z + c₂sin2z
Noe to solve yp, first we need to solve Wronskian
y₁= cos2z , y₂=sin2z
y₁'= -2sin2z , y₂'=2cos2z
⇒ W = \(\left[\begin{array}{ccc}y1&y2\\y1'&y2'\\\end{array}\right]\) = \(\left[\begin{array}{ccc}cos2z&sin2z\\-2sin2z&2cos2z\\\end{array}\right]\)
= (cos2z)(2cos2z)-(-2sin2z)(sin2z)
= 2cos²2z + 2sin²2z
=2 (cos²2z + sin²2z)
= 2 ≠ 0
yp = - y₁\(\int\ {\frac{y2 g(z)}{W} } \, dz\) + y₂\(\int\ {\frac{y1 g(z)}{W} } \, dz\)
= -(cos2z)\(\int\ {\frac{(sin2z)(sec2z)}{2} } \, dz\) + (sin2z)\(\int\ {\frac{(cos2z)(sec2z)}{2} } \, dz\)
= - (cos2z)\(\int\ {\frac{sin2z/cos2z}{2} } \, dz\) + (sin2z)\(\int\ {\frac{cos2z/cos2z}{2} } \, dz\)
= - \(\frac{cos2z}{2}\)\(\int\ {tan2z} \, dz\) + \(\frac{sin2z}{2}\)\(\int\ \,dz\)
= - \(\frac{cos2z}{2}\)(-\(\frac{1}{2}\) ln (cos2z)) + \(\frac{sin2z}{2}\) (z)
= \(\frac{cos2z}{4}\)ln(cos2z) + \(\frac{zsin2z}{2}\)
Now the general equation will become
y = yn + yp
y = c₁cos2z + c₂sin2z +\(\frac{cos2z}{4}\)ln(cos2z) + \(\frac{zsin2z}{2}\) .
To know more about Wronsian here
https://brainly.com/question/16930425
#SPJ4
Find F'(x): F(x) = Sx² 1 (t³ - 4t² + 2)dt
Answers
The derivative of F(x) is F'(x) = 2x³ - 8x² + 4x.
What is function?A relation between a collection of inputs and outputs is known as a function. A function is, to put it simply, a relationship between inputs in which each input is connected to precisely one output.
To find the derivative of the given function F(x), we will apply the fundamental theorem of calculus and differentiate the integral with respect to x.
Let's compute F'(x):
F(x) = ∫[1 to x²] (t³ - 4t² + 2) dt
To differentiate the integral with respect to x, we'll use the Leibniz integral rule:
F'(x) = d/dx ∫[1 to x²] (t³ - 4t² + 2) dt
According to the Leibniz integral rule, we have to apply the chain rule to the upper limit of the integral.
F'(x) = (x²³ - 4x²² + 2) d(x²)/dx - (1³ - 4(1)² + 2) d(1)/dx [applying the chain rule to the upper limit]
F'(x) = (x²³ - 4x²² + 2) (2x) - (1 - 4 + 2) (0) [using the power rule for differentiation]
F'(x) = 2x(x²³ - 4x²² + 2)
F'(x) = 2x³ - 8x² + 4x
Therefore, the derivative of F(x) is F'(x) = 2x³ - 8x² + 4x.
Learn more about function on:
https://brainly.com/question/7693326
#SPJ4
for what points (x0,y0) does theorem a imply that this problem has a unique solution on some interval |x − x0| ≤ h?
Answers
The theorem that we are referring to is likely a theorem related to the existence and uniqueness of solutions to differential equations.
When we say that theorem a implies that the problem has a unique solution on some interval |x − x0| ≤ h, we mean that the conditions of the theorem guarantee the existence of a solution that is unique within that interval. The point (x0, y0) likely represents an initial condition that is necessary for solving the differential equation. It is possible that the theorem requires the function to be continuous and/or differentiable within the interval, and that the initial condition satisfies certain conditions as well. Essentially, the theorem provides us with a set of conditions that must be satisfied for there to be a unique solution to the differential equation within the given interval.
Theorem A implies that a unique solution exists for a problem on an interval |x-x0| ≤ h for the points (x0, y0) if the following conditions are met:
1. The given problem can be expressed as a first-order differential equation of the form dy/dx = f(x, y).
2. The functions f(x, y) and its partial derivative with respect to y, ∂f/∂y, are continuous in a rectangular region R, which includes the point (x0, y0).
3. The point (x0, y0) is within the specified interval |x-x0| ≤ h.
If these conditions are fulfilled, then Theorem A guarantees that the problem has a unique solution on the given interval |x-x0| ≤ h.
To know more about derivative visit:
https://brainly.com/question/30365299
#SPJ11
Let (S,d) be any metric space.(a) Show that if E is a closed subset of a compact set F, then Eis also compact.(b) Show that the finite union of compact sets in S is compact
Answers
a) Since E is closed, its complement F\ E is contained in F, so the intersection of {U_i1, U_i2, ..., U_in} with E is still a finite subcover of E. Thus, E is compact.
b) The union of all these finite subcovers is a finite subcover of {U_i} that covers K, showing that K is compact.
(a) To show that E is compact, we need to show that any open cover of E has a finite subcover. Let {U_i} be an open cover of E. Since E is closed in F, its complement F\E is open in F. Thus, {U_i} and F\ E together form an open cover of F. Since F is compact, there exists a finite subcover {U_i1, U_i2, ..., U_in, F\ E}. Since E is closed, its complement F\ E is contained in F, so the intersection of {U_i1, U_i2, ..., U_in} with E is still a finite subcover of E. Thus, E is compact.
(b) Let K1, K2, ..., Kn be a finite collection of compact subsets of S. Let {U_i} be an open cover of their union K= K1∪ K2 ∪ ... ∪ Kn. Then each Ki is contained in K, so {U_i} is also an open cover of each Ki. Since each Ki is compact, there exists a finite subcover {U_i1, U_i2, ..., U_ik_i} of {U_i} for each Ki. Thus, we have a finite collection of sets {U_i1, U_i2, ..., U_ik_1}, {U_i1, U_i2, ..., U_ik_2}, ..., {U_i1, U_i2, ..., U_ik_n} that covers K1, K2, ..., Kn respectively. The union of all these finite subcovers is a finite subcover of {U_i} that covers K, showing that K is compact.
To learn more about intersection visit;
https://brainly.com/question/14217061
#SPJ11
Darren rolls a fair number cube with 6 faces labeled 1 through 6. He rolls the number cube 180 times. Which TWO events below are most likely? *
Select all that apply.
A. He will roll a 5 or a 6 about 60 times.
B. He will roll a 5 or a 6 exactly 60 times.
C. He will roll an odd number exactly 90 times.
D. He will roll an odd number about 90 times.
E. He will roll a 1 exactly 60 times.
F. He will roll a 1 about 60 times.
Answers
Answer:
Step-by-step explanation:
c.)because it gives more options of numbers and about half the rolls is 90
Find the equation of the line that passes through the points:
(-2, 4) and (1, 10)
Answers
Answer:y=2x+8
Step-by-step explanation:
Convert the decimal, 2.55, into an improper fraction
Answers
Answer:2.55 in fraction form is 51/20.
Step-by-step explanation:
In the diagram below, AC ICB, AB I CD, and mZA = 31°. Find mZB.
С
D
B
You may assume lines that appear straight are straight, but the figure is not otherwise drawn to scale.

Answers
Answer:
m∠B = 59°
Step-by-step explanation:
From ΔADC,
m∠DAC = 31°
By triangle sum theorem,
m∠ADC + m∠DAC + m∠DCA = 180°
90° + 31° + m∠DCA = 180°
m∠DCA = 180° - 121°
= 59°
m∠ACB = m∠ACD + m∠BCD
90° = m∠ACD + 59°
m∠ACD = 90° - 59°
= 31°
In ΔCDB,
m∠CDB + m∠DBC + m∠DCB = 180°
90° + m∠DBC + 31° = 180°
m∠DBC = 180° - 121°
= 59°
Therefore, measure of angle B = 59°.