Answers
(Hopefully it helped)
Answer:
-0.4
hope this helps :)
Related Questions
Aircraft A has 105 more seats than aircraft B. If their total number of seats is 701, find the number of seats for each aircraft.
Aircraft A has how many seats?
Answers
Answer:
Aircraft A: 403 seats
Aircraft B: 298 seats
Step-by-step explanation:
Let's x represent the seats in Aircraft B
We have the equations:
Aircraft A: (x + 105)
Aircraft B: x
We Know
Their total number of seats is 701; find the number of seats for each aircraft.
We Take
x + (x + 105) = 701
2x + 105 = 701
2x = 596
x = 298 seats
So, there are 298 seats in Aircraft B
Aircraft A has how many seats?
We Take
701 - 298 = 403 seats
So, there are 403 seats in Aircraft A
Final Answers:
Aircraft A: 403 seats
Aircraft B: 298 seats
Find the slope of the line passing through the points (6, 4) and (6, -3).
Answers
Answer:
undefined
Step-by-step explanation:
slope = (y_2 - y_1)/(x_2 x_1)
slope = (-3 - 4)/(6 - 6)
slope = -7/0
Since division by zero is undefined, this line has undefined slope.
anushka and arushi are friends. they have equal amount of money. anushka gives arushi 1/3 as a gift. then arushi spends half of her total money, if the money arushi has left is 1600 then whats the amount gifted to arushi. give answer with steps
Answers
Answer: Rs. 3200
Step-by-step explanation:
Let's assume the amount of money they both had before Anushka gives Arushi a gift as "M".
After Anushka gives Arushi 1/3 of her money, Arushi has 1/3 of Anushka's money, which is (1/3)×M.
Then, Arushi spends half of her total money, which means she spends (1/2)×[(1/3)×M] = (1/6)×M.
So now Arushi has (1/3)×M - (1/6)×M = (1/6)×M left.
According to the problem statement, (1/6)×M is equal to 1600. So we can set up an equation:
(1/6)×M = 1600
Multiplying both sides by 6, we get:
M = 9600
So the total amount of money they both had initially was Rs. 9600.
We know that Anushka gave 1/3 of this money to Arushi, which is:
(1/3)×9600 = 3200
Therefore, the amount gifted to Arushi was Rs. 3200.
two planes take off from the same airstrip. the first plane flies west for 150 miles and then flies 30 degrees south of west for 220 miles. the second plane flies east for 220 miles and then flies x degrees south of east for 150 miles. if x < 30, which plane is farther from the airstrip after the second leg? justify your answer.
Answers
The first plane is farther from the airstrip after the second leg
Which plane is farther from the airstrip after the second leg?The first plane
Initial distance = 150 miles west
Additional distance = 220 miles 30 degrees SW
This means that
Additional distance = 220 * cos(30) miles SW
Additional distance = 190.53 miles
Total distance = 150 + 190.53 = 340.53
The second plane
Initial distance = 220 miles east
Additional distance = 150 miles x degrees SE
This means that
Additional distance = 150 * cos(x) miles SW
Total distance = 220 + 150 cos(x)
Given that
x < 30
We have
Second plane < First plane
220 + 150 cos(x) < 340.53
Evaluate
cos(x) < 0.8035
Take the arc cos of both sides
x < 36
x < 36 is not the same as x < 30
Hence, the first plane is farther
Read more about bearing distance at
https://brainly.com/question/22518031
#SPJ1
Which number is less than 22,874?
A. 2.18 x 10^4
B. 2.55 X 10^4
C.2.43 x 10^5
D. 1.78 x 10^6
Answers
Answer:
A. 2.18 × 10^4
Step-by-step explanation:
2.18 × 10^4
10^4 = 10000
2.18 × 10000 = 21800 which is less than 22874
m.
x-intercept =
1/2
and y-intercept = 3
Write an equation for the line in point-slope form and in slope-intercept form
Answers
Answer:
slope intercept form: y= -6x+3
point slope form: y-0= -6(x -1/2)
Step-by-step explanation:
point slope form: y - y1 = m(x - x1)
substitute the values y-0=-6(x-1/2)
slope intercept form:
find the slope using two given points
m = (y2 - y1) / (x2 - x1)
= (3 - 0) / (0 - 1/2)
= 3 / (-1/2)
= -6
substitute into equation
y= -6x+3
What is the sampling method that involves taking a random selection of people from a defined population?.
Answers
A sampling method is simple random sampling.
What is sampling method?In statistical analysis, sampling is the procedure by which researchers choose a specific number of observations from a larger population. The sample strategy will depend on the sort of study being done, although it may involve systematic sampling or just plain random sampling.
A selection of participants from a population are chosen at random by the researcher using simple random sampling, a sort of probability sampling. Every person in the population has the same probability of getting chosen. Then, data are gathered from as much of this randomly selected subgroup as feasible.
Since it only uses one random pick and is very simple, this method is the easiest of all the probability sampling techniques.
To know more about sampling method check the link: brainly.com/question/12902833
#SPJ4
A certain type of kickboard scooter comes in silver, red, 2
or purple with wheel sizes of 125 millimeters or 180
millimeters. Determine the total number of color-wheel size combinations.
(This is probability and I’m having such a hell of a time figuring it out pls help)
Answers
There are a total of 8 color-wheel size combinations for the kickboard scooter. This means that customers have 8 different options to choose from when selecting the color and wheel size for their scooter.
To determine the total number of color-wheel size combinations for the kickboard scooter, we need to multiply the number of color options by the number of wheel size options.
Given that there are 4 color options (silver, red, blue, and purple) and 2 wheel size options (125mm and 180mm), we can use the multiplication principle to find the total number of combinations:
Total combinations = Number of color options × Number of wheel size options
Total combinations = 4 colors × 2 wheel sizes
Total combinations = 8
There are a total of 8 color-wheel size combinations for the kickboard scooter. This means that customers have 8 different options to choose from when selecting the color and wheel size for their scooter.
For more such questions on combinations
https://brainly.com/question/28065038
#SPJ8
A rectangular living room has a perimeter of 40 meters. It’s area is 100 square meters.what are the dimensions of the living room
Answers
Answer:
Step-by-step explanation:
Firstly, I presume that the question talks about a rectangle and there is consistency in units i.e.Area is in units^2 and perimeter is in units (else there is no possible solution).
Now, perimeter = 2(L+B) = 40
OR (L+B) = 20.
Also, area = LxB = 100.
Now, LxB = 100 will give you the following values for LxB (Note in a rectangle, L>B or L=B):- (100×1),(50×20),(25x4),(20×5),(10×10).
Only one value gives L+B = 20 viz.L=10 & B=10.
Hope this helps! :)
(This was by another user you can search it up and see.)
Using 50 random numbers given below, compute the mean and standard deviation. 0.937776 0.270012 0.243785 0.590701 0.824982 0.131805 0.879337 0.741998 0.254683 0.080259 0.419321 0.928220 0.958430 0.980182 0.263900 0.063119 0.762096 0.485612 0.662900 0.362242 0.724796 0.307736 0.305021 0.417052 0.054337 0.323357 0.069662 0.843387 0.353107 0.074262 0.735596 0.175095 0.390508 0.668932 0.029861 0.205228 0.387740 0.962169 0.646565 0.423914 0.754782 0.156719 0.773113 0.546335 0.323573 0.649740 0.214082 0.382383 0.383982 0.030539 Mean = (to 6 decimals) Standard deviation = (to 6 decimals)
Answers
The mean is 0.477514 (rounded to 6 decimal places).
The standard deviation is 0.288919 (rounded to 6 decimal places).
How to Solve the Problem?To calculate the mean and standard deviation, we will use the following formulas:
Mean = (sum of all values) / (number of values)
Standard deviation = sqrt[(sum of (value - mean)^2) / (number of values)]
Using these formulas, we can calculate the mean and standard deviation for the given set of random numbers:
Mean = (0.937776 + 0.270012 + 0.243785 + 0.590701 + 0.824982 + 0.131805 + 0.879337 + 0.741998 + 0.254683 + 0.080259 + 0.419321 + 0.928220 + 0.958430 + 0.980182 + 0.263900 + 0.063119 + 0.762096 + 0.485612 + 0.662900 + 0.362242 + 0.724796 + 0.307736 + 0.305021 + 0.417052 + 0.054337 + 0.323357 + 0.069662 + 0.843387 + 0.353107 + 0.074262 + 0.735596 + 0.175095 + 0.390508 + 0.668932 + 0.029861 + 0.205228 + 0.387740 + 0.962169 + 0.646565 + 0.423914 + 0.754782 + 0.156719 + 0.773113 + 0.546335 + 0.323573 + 0.649740 + 0.214082 + 0.382383 + 0.383982 + 0.030539) / 50 = 0.477514
Therefore, the mean is 0.477514 (rounded to 6 decimal places).
Now we will calculate the standard deviation:
Standard deviation = sqrt[((0.937776 - 0.477514)^2 + (0.270012 - 0.477514)^2 + (0.243785 - 0.477514)^2 + ... + (0.382383 - 0.477514)^2 + (0.383982 - 0.477514)^2 + (0.030539 - 0.477514)^2) / 50] = 0.288919
Therefore, the standard deviation is 0.288919 (rounded to 6 decimal places).
Learn more about mean here: https://brainly.com/question/20118982
#SPJ1
2/7 of 5/6 (3 1/3 * 2/5) by 1/5 equals to
Answers
\( \frac{2}{7} \times \frac{5}{6} ( \frac{10}{3} \times \frac{2}{5} ) \times \frac{1}{5} \\ = \frac{2}{7} \times \frac{5}{6} ( \frac{20}{15} ) \times \frac{1}{5} \\ = \frac{2}{7} \times \frac{100}{90} \times \frac{1}{5} \\ = ( \frac{2}{7} \times \frac{10}{9}) \times \frac{1}{5} \\ = \frac{20}{63} \times \frac{1}{5} \\ = \frac{20}{315} \\ = \frac{4}{63} \)
ATTACHED IS THE SOLUTION
Please can someone who knows the right answer help me? From a group of 5 boys and 3 girls, a boy and a girl will be selected to attend a conference. In how many ways can the select be made?
Answers
The selection can be made in 15 different ways, taking into account the distinct combinations of a boy and a girl from the given group of 5 boys and 3 girls.
To determine the number of ways a boy and a girl can be selected from a group of 5 boys and 3 girls to attend a conference, we can use the concept of combinations.
The number of ways to choose one boy from 5 boys is 5C1, which is equal to 5. Similarly, the number of ways to choose one girl from 3 girls is 3C1, which is equal to 3.
To select one boy and one girl, we need to multiply the number of ways to choose a boy and a girl together. Using the multiplication principle, we multiply the number of choices for each category: 5C1 * 3C1 = 5 * 3 = 15.
Therefore, there are 15 ways to select a boy and a girl from the given group to attend the conference.
Each combination represents a unique pair consisting of one boy and one girl. For example, if the boys are labeled as B1, B2, B3, B4, and B5, and the girls are labeled as G1, G2, and G3, the possible pairs could be (B1, G1), (B1, G2), (B1, G3), (B2, G1), (B2, G2), and so on, up to (B5, G3).
For more such question on selection. visit :
https://brainly.com/question/251701
#SPJ8
Nicole was shopping at a local department store and had a budget of $60. She was
buying shorts (s) priced at $10 and t-shirts (t) priced at $8. She was heading to the
checkout stand when she saw a sign that said all t-shirts are 40% off. Write and simplify
an equation that Nicole could use to find the possible combinations of shorts and t-shirts
she could buy for $60.
Answers
Answe YEAH BOIIIIII!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
. A manufacturer of salad dressings uses machines to dispense liquid ingredients into bottles that move along a filling line. The machine that dispenses salad dressings is working properly when 8 ounces are dispensed. Suppose that the average amount dispensed in a particular sample of 35 bottles is 7.91 ounces with a variance of 0.03 ounces squared. Is there evidence that the machine should be stopped and production wait for repairs
Answers
Answer:
The calculated value |t| = |-3.082| =3.082 > 2.0322 at 0.05 level of significance
The null hypothesis is rejected
An alternative hypothesis is accepted
There is evidence that the machine should be stopped and production wait for repairs
Step-by-step explanation:
Step(i):-
Given that the mean of the Population(μ) = 8 ounces
Given that the sample size 'n' = 35
The mean of the sample(x⁻) = 7.91
The variance of the sample S² = 0.03 ounces
S = √0.03 = 0.1732
Step(ii):-
Null Hypothesis: H₀: There is no evidence that the machine should be stopped and production wait for repairs
Alternative Hypothesis: H₁: There is evidence that the machine should be stopped and production wait for repairs
\(t = \frac{x^{-} -mean}{\frac{S}{\sqrt{n} } }\)
\(t = \frac{7.91 -8}{\frac{0.1732}{\sqrt{35} } }\)
t = - 3.082
|t| = |-3.082| =3.082
Degrees of freedom
ν = n-1 = 35-1=34
t₀.₀₅ = 2.0322
The calculated value |t| = |-3.082| =3.082 > 2.0322 at 0.05 level of significance
The null hypothesis is rejected
An alternative hypothesis is accepted
conclusion:-
There is evidence that the machine should be stopped and production wait for repairs
-8/9 + (-2)/57
find the absolute value of the following rational number
Answers
The absolute value of the Rational number -474/513 is 474/513.
To find the sum of the rational numbers -8/9 and -2/57, you need to have a common denominator. The least common multiple (LCM) of 9 and 57 is 513. So, you can rewrite the fractions with a common denominator:
-8/9 = (-8/9) * (57/57) = -456/513
-2/57 = (-2/57) * (9/9) = -18/513
Now, you can add the fractions:
-456/513 + (-18/513) = (-456 - 18)/513 = -474/513
To find the absolute value of the rational number -474/513, you simply ignore the negative sign and take the value as positive:
| -474/513 | = 474/513
Therefore, the absolute value of the rational number -474/513 is 474/513.
For more questions on Rational .
https://brainly.com/question/30339525
#SPJ8
The point P=(1/2,y)lies on the unit circle shown below. What is the value of y in simplest form?
Answers
The value of y in simplest form for the point P = (1/2, y) lying on the unit circle is y = ± √(3)/2.
To find the value of y in simplest form for the point P = (1/2, y) lying on the unit circle, we can use the equation of the unit circle, which states that for any point (x, y) on the unit circle, the following equation holds: x^2 + y^2 = 1.
Plugging in the coordinates of the point P = (1/2, y), we get:
(1/2)^2 + y^2 = 1
1/4 + y^2 = 1
y^2 = 1 - 1/4
y^2 = 3/4.
To simplify y^2 = 3/4, we take the square root of both sides:y = ± √(3/4).
Now, we need to simplify √(3/4). Since 3 and 4 share a common factor of 1, we can simplify further: y = ± √(3/4) = ± √(3)/√(4) = ± √(3)/2.
for more search question point
https://brainly.com/question/28162977
#SPJ8
Marianna finds an annuity that pays 8% annual interest, compounded quarterly. She invests in this annuity and contributes $10,000 each quarter for 6 years. How much money will be in her annuity after 6 years? Enter your answer rounded to the nearest hundred dollars.
Answers
The amount of money in Marianna's annuity after 6 years will be approximately $300,516.
To calculate the amount of money in Marianna's annuity after 6 years, we can use the formula for compound interest on an annuity:
A = P * ((1 + r/n)^(n*t) - 1) / (r/n)
Where:
A = the final amount in the annuity
P = the regular contribution (each quarter) = $10,000
r = annual interest rate = 8% = 0.08
n = number of compounding periods per year = 4 (since it's compounded quarterly)
t = number of years = 6
Plugging in the values:
A = 10000 * ((1 + 0.08/4)^(4*6) - 1) / (0.08/4)
Calculating this expression:
A ≈ 10000 * ((1.02)^24 - 1) / 0.02
A ≈ 10000 * (1.601032449136241 - 1) / 0.02
A ≈ 10000 * 0.601032449136241 / 0.02
A ≈ 10000 * 30.05162245681205
A ≈ 300,516.22
For more such questions on annuity,click on
https://brainly.com/question/25792915
#SPJ8
Answer:
304200
Step-by-step explanation:
To find the value of P6, use the savings annuity formula
PN=d((1+r/k)N k−1)r/k.
From the question, we know that r=0.08, d=$10,000, k=4 compounding periods per year, and N=6 years. Substitute these values into the formula gives
P6=$10,000 ((1+0.08/4)6⋅4−1)/(0.08/4).
Simplifying further gives P6=$10,000 ((1.02)24−1)/(0.02) and thus P6=$304,218.62.
Rounding as requested, our answer is 304200.
A survey of 800 school employees yielded the following information 430 were instructors 595 were full time faculty and 340 of the instructors were full time
Answers
249
Step-by-step explanation:
let n(U) be the total number of school
employees =800
Let n(1) be amount of instructors = 430
Let (F) be full-time faculty = 589
Let n(InF) be the instructors who were full-time
faculty = 340
The number of employees who were full-time
faculty but were not instructors is expressed as:
n(FnI") = n(F) - n(InF)
n(FnI') = 589 - 340
n(FnI'") = 249
Hence the number of school employees who
were full-time faculty but were not instructors
are 249
What time des the clock show?

Answers
Answer:
8:03 time des the clock .
5
Select the correct answer.
Which criterion, if any, could prove the triangles are congruent?
OA.
ASA
OB
SAS
Oc.
HL
OD.
none

Answers
Answer:
I could be wrong, but I believe that the answer is D, none. This is because there is only proof of one congruent side and angle.
Step-by-step explanation:
None of the options can prove that the triangles are congruent so option (D) will be correct.
What is congruence?If two figures are exactly the same in sense of their length side all things then they will be congruent.
If it is possible to superimpose one geometric figure on the other so that their entire surface coincides, that geometric figure is said to be congruent or to be in the relation of congruence.
In other meaning, if you can copy a figure then that copy and the original figure will be congruent.
In the given figure only one side and one angle are the same.
But for congruency three pairs should be the same which is not present in the figure hence none of the above is valid
To learn more about congruent,
https://brainly.com/question/12413243
#SPJ5
7. For the three-part question that follows, provide your answer to each part in the given workspace. Identify each part with a coordinating re
A, Part B, and Part C.
in.
Part A: Determine the value of the diameter of the circle shown above.
Part B: Determine the value of the radius of the circle shown above.
Part C: Explain your reasoning for Part A and Part B of this problem.
- AA- A
B
U Font Family
FE E
C
1
D
1+
4
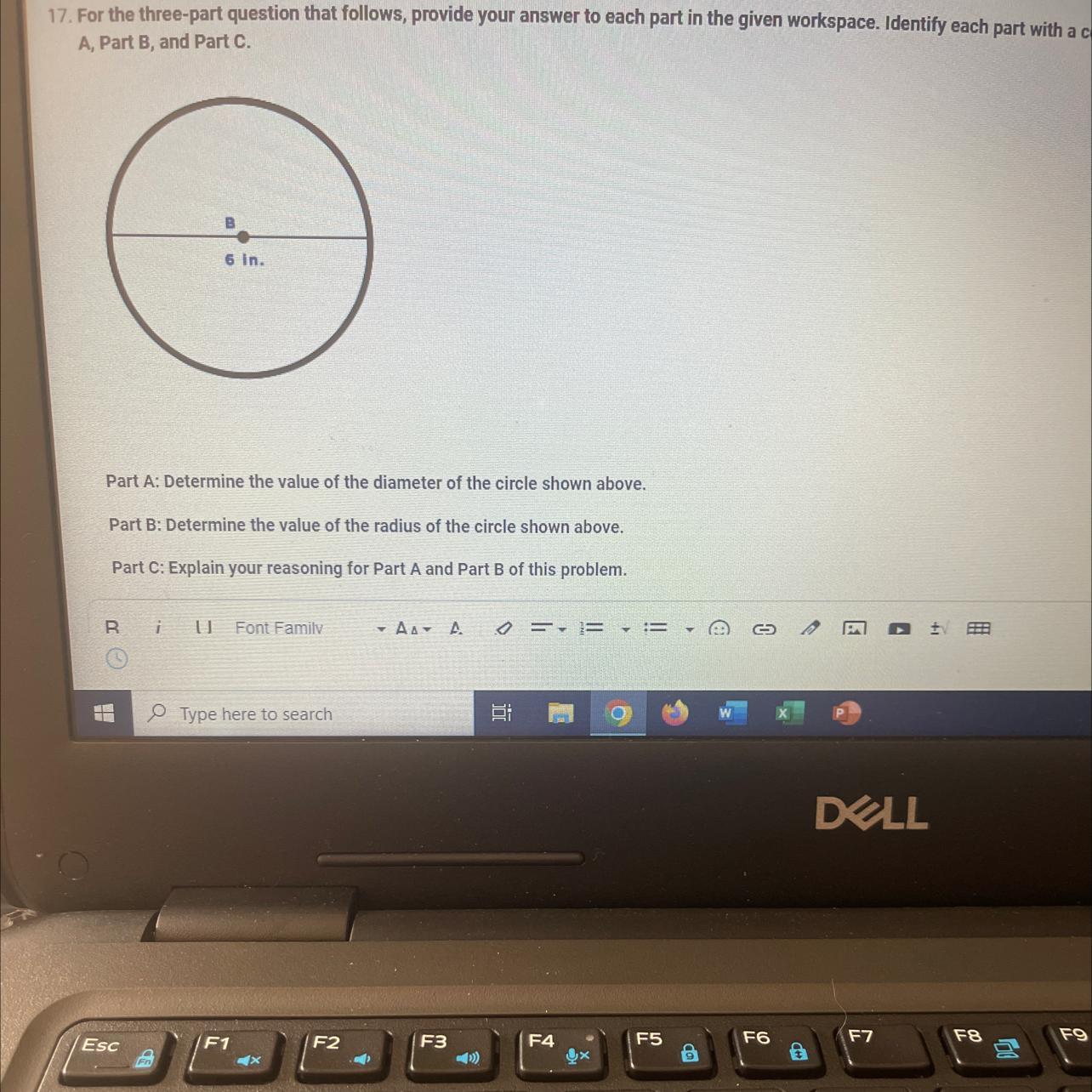
Answers
Answer:
A: The diameter is 6in.
B: The radius is 3in.
C: The diameter is given to us in the problem. A line is drawn out that strikes through the center point. of the circle, and it is labeled 6in in the middle, so we can deduce that it is the diameter. The radius of a circle is 1/2 the length of the diameter, so 6/2 = 3in. If the 6in was on either side of the line, then that would be labeling the radius.
Suppose you are given a rectangular piece of cardboard having length 6x+2 inches and width 2x−4 inches. Then you cut out a square from this piece of cardboard having side length x inches. Find the area of the remaining piece of cardboard expressed in terms of x.
Answers
To determine the area of the remaining piece of cardboard expressed in terms of x when a square of side length x inches is cut out from a rectangular piece of cardboard having a length of 6x+2 inches and a width of 2x-4 inches, use the following steps.
Draw and label a diagram of the problem. The rectangle should be labeled as 6x+2 inches by 2x-4 inches, and the square cut out should be labeled as x inches by x inches. This is how the diagram looks like: Determine the area of the rectangle, Arect.
The area of the rectangle is given by the product of its length and width. Thus, Arect = (6x + 2)(2x - 4) Determine the area of the square, Asq. The area of the square is given by the square of its side length. Thus, Asq = x²Step 4: Determine the area of the remaining cardboard after the square is cut out, Ar.
This is the difference between the area of the rectangle and the area of the square. Thus, Ar = Arect - Asq= (6x + 2)(2x - 4) - x²= 12x² - 20x - 16
Simplify the expression. The final answer is given in terms of x. Thus, Ar = 12x² - 20x - 16.The area of the remaining piece of cardboard is expressed in terms of x as 12x² - 20x - 16.
For more such questions on square
https://brainly.com/question/27307830
#SPJ8
what is the volume of the cylinder below height 15 radius 11
Answers
Answer:
πr^2 h
π(11)^2 (15)
= 1815π or = 5701
I NEED HELP PLEASE!!!!!!!!
Examine the following step function.
Which statements are true?
Select all that apply.

Answers
The statements that are true include the following:
B. It is the ceiling function.
D. Any decimal or fraction round to the least integer that is greater than x.
What is a piecewise-defined function?In Mathematics, a piecewise-defined function can be defined as a type of function that is defined by two (2) or more mathematical expressions over a specific domain.
Generally speaking, the domain of any piecewise-defined function simply refers to the union of all of its sub-domains. By critically observing the graph of the given piecewise-defined function, we can reasonably infer and logically deduce that it is the ceiling function (least integer function) because it comprises the smallest integer that cannot be smaller than x i.e it assigns a decimal or fraction to the next integer;
x = 1.3 ≈ 2
x = 9 ≈ 9
Read more on piecewise function here: brainly.com/question/18670055
#SPJ1
(40 POINTS) A newly hired lawyer receives a $15,000 signing bonus from a law firm and invests the money in a savings account at 4.75% interest. After 42 months, the lawyer checks the account balance.
Part A: Calculate the interest earned, to the nearest dollar, if the interest is compounded quarterly. Show all work. (2 points)
Part B: Calculate the interest earned, to the nearest dollar, if the interest is compounded continuously. Show all work. (2 points)
Part C: Using the values from Part A and Part B, compare the interest earned for each account by finding the difference in the amount of interest earned. (1 point)
Answers
Answer:
after 42 months he has $2,696 in interest
compound quarterly is equivalent to annual rate of 4.835%
Part b
after 42 months he has $2,713 compound continuously
the diffrence is $17
15000 + 4.75% · 42 compound quarterly is $2,696
15000 + 4.75% · 42 compound continuously is $2,696
Answer:
Step-by-step explanation:
Stop posting FLVS questions on this website. It is illegal, and you can be expelled from the program. :)
The Venn diagram shows the number of customers who have purchased different types of pets from a pet store, where C represents customers who have purchased cats, D represents customers who have purchased dogs, and F represents customers who have purchased fish.
Circles C, D, and F overlap. Circle C contains 15, circle D contains 21, and circle F contains 12. The overlap of C and F contains 2, the overlap of F and D contains 0, and the overlap of D and C contains 3. The overlap of all 3 circles contains 1. Number 14 is outside of the circles.
How many people are in the set C ∩ D?
4
6
36
38
Answers
The number of people in the set C ∩ D (customers who purchased both cats and dogs) is obtained by adding the overlap of D and C (3) with the overlap of all 3 circles (1), resulting in a total of 4 individuals.
The correct answer is 4.
To determine the number of people in the set C ∩ D (customers who have purchased both cats and dogs), we need to analyze the overlapping regions in the Venn diagram.
Given information:
- Circle C (cats): 15
- Circle D (dogs): 21
- Circle F (fish): 12
- Overlap of C and F: 2
- Overlap of F and D: 0
- Overlap of D and C: 3
- Overlap of all 3 circles: 1
- Number outside of circles: 14
To determine the number of people in the set C ∩ D (customers who have purchased both cats and dogs), we need to consider the overlapping region between circles C and D.
From the information given, we know that the overlap of D and C is 3. Additionally, we have the overlap of all 3 circles, which is 1. The overlap of all 3 circles includes the region where customers have purchased cats, dogs, and fish.
To calculate the number of people in the set C ∩ D, we add the overlap of D and C (3) to the overlap of all 3 circles (1). This gives us 3 + 1 = 4.
Therefore, from the options given correct one is 4.
For more such information on: set
https://brainly.com/question/24713052
#SPJ8
Answer: 4
Step-by-step explanation:
trust me bro
Solve for x. Enter your answer in the box below as a fraction in lowest terms,
using the slash ( / ) as the fraction bar.
6/9+x=7/10
Answers

Find the area of the shaded portion in the equilateral triangle with sides 6. Show all work for full credit.
(Hint: Assume that the central point of each arc is its corresponding vertex.)
Answers
The area of the shaded portion in the equilateral triangle with sides 6 is 9√3 - 36π.
To find the area of the shaded portion in the equilateral triangle, we need to determine the area of the three arcs and subtract it from the area of the equilateral triangle.
First, let's find the area of one arc. Each arc has a radius equal to the length of the side of the equilateral triangle, which is 6. The formula for the area of a sector is A = (θ/360)πr², where θ is the central angle in degrees.
In an equilateral triangle, each interior angle measures 60 degrees, so the central angle of the arc is 120 degrees (360 degrees divided by 3). Plugging these values into the formula, we get A_arc = (120/360)π(6)² = (1/3)π(6)² = 12π.
Since there are three identical arcs, the total area of the arcs is 3 times the area of one arc, which is 3(12π) = 36π.
Now, let's find the area of the equilateral triangle. The formula for the area of an equilateral triangle is A_triangle = (√3/4)s², where s is the length of a side.
Plugging in the value of the side length, we have A_triangle = (√3/4)(6)² = (√3/4)(36) = 9√3.
Finally, we subtract the area of the arcs from the area of the equilateral triangle to find the shaded portion's area: A_shaded = A_triangle - A_arc = 9√3 - 36π.
For more such questions on triangle
https://brainly.com/question/1058720
#SPJ8
Someone out here know the answer?

Answers
Answer:
k = -5
Step-by-step explanation:
f(9) = 2/3*9 +k
f(9) = 6+k
k = -5
A bag contains k blue beads and 4 red ones, If the probability of randomly picking a blue bead from it is 1/3, find the value of k
Answers
Answer:
\(k = 2\)
Step-by-step explanation:
\(\textrm{P(blue \;bead)} = \dfrac{\textrm{Number of blue beads}}{\textrm{Total number of beads}}\\\\\textrm {Number of blue beads } = k\\\\\textrm{Total number of beads } = k + 4\\\\\)
\(\textrm{P(blue \;bead)} = \dfrac{k}{k+4}\\\\\)
\(\textrm{We are given this probability as } \dfrac{1}{3}\\\\\textrm{So,}\\\\\dfrac{k}{k+4} = \dfrac{1}{3}\\\\\)
Cross-Multiplying this equation we get
\(k\cdot 3 = 1 \cdot (k + 4)\\\\\longrightarrow 3k = k + 4\\\\3k - k = 4\\\\2k = 4\\\\k = 2\\\\\)
