Use Lagrange multipliers to find the absolute maximum value and absolute minimum value of f(x, y) = 2x 2 + 2y subject to x 2 + 2y + y 2 = 15.
Answers
Answer:
Maximum absolute value of f=61/2 at (\(3/2\sqrt{7},-1/2\)) and (\(-3/2\sqrt{7},-1/2\))
Minimum absolute value of f=-10 at (0,-5)
Step-by-step explanation:
We are given that
\(f(x,y)=2x^2+2y\)
Let
\(g(x,y)=x^2+2y+y^2-15=0\)
\(\nabla f(x,y)=<4x,2>\)
\(\nabla g(x,y)=<2x,2+2y>\)
Using Lagrange multipliers
\(f_x(x,y)=\lambda g_x(x,y)\)
\(4x=2x\lambda\)
\(4x-2x\lambda=2x(2-\lambda)=0\)
x=0 or
\(\lambda=2\)
If x=0
Then,
\(y^2+2y-15=0\)
\(y^2+5y-3y-15=0\)
\(y(y+5)-3(y+5)=0\)
\((y+5)(y-3)=0\)
\(y=-5,3\)
\(2=(2+2y)\lambda\)
If \(\lambda=2\)
\(2=2(2+2y)\)
\(2/2=2+2y\)
\(1=2+2y\)
\(2y=1-2=-1\)
\(y=-\frac{1}{2}\)
If y=-1/2
Then,
\(x^2-1+1/4=15\)
\(x^2+(\frac{-4+1}{4})=15\)
\(x^2-\frac{3}{4}=15\)
\(x^2=15+3/4=\frac{60+3}{4}=\frac{63}{4}\)
\(x=\pm\frac{3\sqrt{7}}{2}\)
Therefore, possible extreme points are
(0,-5),(0,3),(\(3/2\sqrt{7},-1/2\)) and (\(-3/2\sqrt{7},-1/2\))
\(f(0,-5)=2(0)+2(-5)=-10\)
\(f(0,3)=2(3)=6\)
\(f(3/2\sqrt{7},-1/2)=\frac{63}{2}-1=\frac{61}{2}\)
\(f(-3/2\sqrt{7},-1/2)=\frac{63}{2}-1=\frac{61}{2}\)
Therefore, maximum absolute value of f=61/2 at (\(3/2\sqrt{7},-1/2\)) and (\(-3/2\sqrt{7},-1/2\))
Minimum absolute value of f=-10 at (0,-5)
Related Questions
Which of the following z-scores is NOT outside the middle 68% of the data for a normal distribution?
a.) -0.8
b.) -2.8
c.) 1.8
d.) 3.8
Answers
Answer:
Step-by-step explanation:
A, use three_digite rounding arithmetic to compute 13- 6 and determine the absolute,relative ,and percentage errors.
tepeat part (b) using three – digit chopping arithmetic.
See question in screenshot below.
Answers
The equation of the transformation of the exponential function y = 2ˣ in the form y = A·2ˣ + k, obtained from the simultaneous found using the points on the graph is y = (-2)·2ˣ + 3
What is an exponential equation?An exponential equation is an equation that has exponents that consists of variables.
The given equation is y = 2ˣ
The equation for the transformation is; y = A·2ˣ + k
The points on the graphs are;
(0, 1), (1, -1) and (2, -5)
Plugging the x and y-values to find the value A and k gives the following simultaneous equations;
When x = 0, y = 1, therefore;
1 = A·2⁰ + k = A + k
1 = A + k...(1)
When x = 1, y = -1, which gives;
-1 = A·2¹ + k
-1 = 2·A + k...(2)
Subtracting equation (1) from equation (2) gives;
-1 - 1 = 2·A - A + k - k
-2 = A
1 = A + k, therefore;
1 = -2 + k
k = 2 + 1 = 3
k = 3
Which gives;
y = -2·2ˣ + 3 = 3 - 2·2ˣ
Learn more about the solutions to simultaneous equations here:
https://brainly.com/question/26310043
#SPJ1
.please help meeeeeee
Answers
6. 1.84 x 10^3
7. 104
8. 567
9. 23
. The pet store salesman told Evan to feed his dog 8 ounces of food per day. The food is sold in pounds. How many pounds does Evan need to buy for 2 weeks of feeding his dog? (16 ounces = 1 pound)?
Answers
What is the value of y?
Answers
Answer:
y = 20
Step-by-step explanation:
The measure of angle A is such that the sum of the two congruent base angles and A is 180°.
2(25°) +(3y+70)° = 180°
3y +120 = 180 . . . . . . . . . . . divide by ° and simplify
3y = 60 . . . . . . . . . . . . subtract 120
y = 20 . . . . . . . . . .divide by 3
__
The value of x is 5.
Can someone help me Solve:
-2√3+√75=
Answers
Answer:
\(3\sqrt{3}\)------------------
Simplify in below steps:
\(-2\sqrt{3} +\sqrt{75} =\)\(-2\sqrt{3} +\sqrt{25*3} =\)\(-2\sqrt{3} +\sqrt{5^2*3} =\)\(-2\sqrt{3} +5\sqrt{3} =\)\(3\sqrt{3}\)HELP ASAP PLSS!!
I think it’s b I’m not so sure
Answers
Answer:
Step-by-step explanation: I think it is 'b' too (sorry if wrong)
What is the perimeter of the parallelogram?
Answers
Answer:
P= 2 (a+b)
Step-by-step explanation:
Find x (circle)
(Btw I don’t know if 5.6 is correct so just ignore that)
Answers
Answer:
A. 11.2
Step-by-step explanation:
But this has nothing to do with 5.6 × 2. Erase that! Lol.
You have a right triangle here. The only thing to do with the circle is that there are two radii (plural of radius) shown. So they have to be the same measure.
The unmarked "bottom" of the triangle, the short leg, is a radius, so it too, is 8.4.
The hypotenuse of the right triangle, the side on the right, the longest side is 5.6 + 8.4.
The hypotenuse is 14.
Let's do some Pythagorean Theorem.
Leg^2+ leg^2=hypotenuse^2
you know,
a^2 + b^2 = c^2
fill in what we know.
8.4^2 + b^2 = 14^2
simplify.
70.56 + b^2 = 196
subtract 70.56
b^2 = 125.44
squareroot both sides
b = 11.2
Consider two points A(0,0) and B(1, 1) on a Cartesian plane. The equation of the axis of the segment AB is: A. y = 1 2 − B. y = 2 − C. y = 1 − 2 D. y = 1 − E. y = 1 − 2
Answers
So, the equation of the axis of the segment AB is (A) y = 1/2 - x/2.
What is slope?
In mathematics, slope refers to the steepness or incline of a line on a graph. It is a measure of how much the dependent variable changes for every unit change in the independent variable.
The slope of the line passing through points A and B can be calculated as follows:
slope = (change in y) / (change in x) = (1-0) / (1-0) = 1/1 = 1
The equation of a line in slope-intercept form (y = mx + b), where m is the slope and b is the y-intercept.
To find the y-intercept, we can use point A (0,0) and substitute the slope value.
y = mx + b
0 = 1(0) + b
b = 0
Therefore, the equation of the line passing through points A and B is:
y = 1x + 0
Simplifying, we get:
y = x
So, the answer is (A) y = 1/2 - x/2. However, this is not one of the given answer choices. We can also write the equation in point-slope form as y - y1 = m(x - x1) using point A, which gives:
y - 0 = 1(x - 0)
y = x
This confirms our earlier answer.
To learn more about slope from the given link:
https://brainly.com/question/2491620
#SPJ1
Write an explicit formula for an, the nth term of the sequence 6, 14, 22, ....
Answers
Answer:
\(a_{n}\) = 8n - 2
Step-by-step explanation:
The sequence has a common difference between consecutive terms , that is
14 - 6 = 22 - 14 = 8
This indicates the sequence is arithmetic with explicit formula
\(a_{n}\) = a₁ + (n - 1)d
where a₁ is the first term and d the common difference
Here a₁ = 6 and d = 8 , then
\(a_{n}\) = 6 + 8(n - 1) = 6 + 8n - 8 = 8n - 2
Not sure on how to do this. Could really use some help. (There is 2 parts to this question)
Answers
The figure attached is composed of a cylinder and an sphere. Then:
Surface Area = Total Area of the Sphere + Side Area of the Cylinder.
Hence:
\(\begin{gathered} A_{sphere}=4πr^2 \\ A_{sphere}=4\times\pi\times8^2 \\ A_{sphere}=804.25cm^2 \end{gathered}\)Now, the side area of the cylinder:
\(\begin{gathered} SA_{cylinder}=2\timesπ\times r\times h \\ SA_{cylinder}=2\timesπ\times8\times12.5 \\ SA_{cylinder}=628.32cm^2 \end{gathered}\)Finally:
\(SA=804.25+628.32=1432.57cm^2\)ANSWER
The surface area is 1432.6 cm²
Now, to find the volume:
Total Volume = Volume of the Sphere + Volume of the Cylinder
Volume of the Sphere:
\(\begin{gathered} V_{sphere}=\frac{4}{3}πr³ \\ V_{sphere}=\frac{4}{3}\pi\times8^3=2144.66cm^3 \end{gathered}\)Volume of the Cylinder:
\(\begin{gathered} V_{cylinder}=πr²h \\ V_{cylinder}=π\times8^2\times12.5=2513.27cm^3 \end{gathered}\)Finally:
\(V=2144.66+2513.27=4657.93cm^3\)ANSWER
The volume is 4657.9cm³
3 to the power of 5 = 243. Explain how to use that fact to quickly evaluate 3 to the power of 6
Answers
Step-by-step explanation:
3^6 = 3 * 3^5
= 3 * 243 = 729
You want to buy a $34,000 car. The company is offering a 2% interest rate for 60 months (5 years). What willyour monthly payments be?
Answers
We have to calculate the monthly payments for an annuity of $34,000 with a 2% interest rate for 60 months.
We then can express the monthly payment as:
\(\text{PMT}=\frac{PV\cdot\frac{r}{m}}{1-(1+\frac{r}{m})^{-n\cdot m}}\)where PV = 34000, r = 0.02 (the annual interest rate in decimal form), m = 12 (number of subperiods per year) and n = 5 (the number of annual periods).
We can replace with the values and solve for PMT as:
\(\begin{gathered} \text{PMT}=\frac{34000\cdot\frac{0.02}{12}}{1-(1+\frac{0.02}{12})^{-5\cdot12}} \\ \text{PMT}\approx\frac{34000\cdot0.00167}{1-(1.00167)^{-60}} \\ \text{PMT}\approx\frac{56.67}{1-0.905} \\ \text{PMT}\approx\frac{56.67}{0.095} \\ \text{PMT}\approx595.94 \end{gathered}\)Answer: the monthly payments will be approximately $595.94.
Need help ASAP due in 7 minutes
Will make you brainlist
Answers
Answer:
A
Step-by-step explanation:
A is the only answer with ordered pairs that have a consistent rate of change, -1/3
A spinner has 4 equal sectors colored yellow, blue, green, and red. If in 100 spins we get
28 blue (B), 25 red (R), 29 green (G), and 18 yellow (Y) outcomes, find the empirical probability of getting color P(R).
O A. 6/25
OB. 1/4
O C. 3/10
O D. 13/50
Answers
Answer:
B
Step-by-step explanation:
28+25+29+18 = 100
red = 25
25/100 = 1/4
The required empirical probability is 1/4 which gets the color of red P(R).
What is probability?The probability is defined as the possibility of an event being equal to the ratio of the number of favorable outcomes and the total number of outcomes.
A spinner has 4 equal sectors colored yellow, blue, green, and red. If in 100 spins we get
28 blue (B), 25 red (R), 29 green (G), and 18 yellow (Y) outcomes
To find the empirical probability of getting a red outcome, we need to divide the number of red outcomes by the total number of spins:
P(R) = 25 red outcomes / 100 spins
Apply the division operation, and we get
P(R) = 1/4
Hence, the required empirical probability is 1/4
Therefore, the correct answer is 1/4 or option B.
Learn more about probability here:
brainly.com/question/11234923
#SPJ2
On the coordinate plane, the endpoints of a line segment are (9, 5) and (3, 7). What is the midpoint of the line segment?
Answers
Answer:
(6, 6)
Step-by-step explanation:
The formula to find midpoint is (xm, ym) = (x1+x2)/2, (y1+y2)/2
In this case, x1= 9
x2= 3
y1= 5
and y2= 7
so, (xm, ym) = (9+3)/2, (5+7)/2
which can be simplified to
(xm, ym)= 12/2, 12/2
which equals (xm, ym) = 6,6
so the x value of the midpoint is 6 and the y value of the midpoint is 6
which makes the midpoint (6,6)
Help me please, Domain & Range problem
Answers
Answer:
Domain: all reals
Range: 4 ≤y <∞
Step-by-step explanation:
The domain is the possible input values(x)
From the arrows at the left and right ends on the graph, the inputs can be all reals
The range is the possible output values (y)
Y goes from 4 to infinity
4 ≤y <∞
What is the M.A.D. (mean absolute deviation) of the following data set?
8 9 9 7 8 6 9 8
Answers
The mean absolute deviation is 0.75
How to determine the mean absolute deviationTo calculate the mean absolute deviation (M.A.D.), you need to find the average of the absolute differences between each data point and the mean of the data set
From the information given, we have that the data set is;
8 9 9 7 8 6 9 8
Let's calculate the mean, we get;
Mean = (8 + 9 + 9 + 7 + 8 + 6 + 9 + 8) / 8
Mean = 64 / 8
Divide the values
Mean = 8
Let's determine the absolute difference, we get;
Absolute differences=
|8 - 8| = 0
|9 - 8| = 1
|9 - 8| = 1
|7 - 8| = 1
|8 - 8| = 0
|6 - 8| = 2
|9 - 8| = 1
|8 - 8| = 0
Find the mean of the absolute differences:
Average of absolute differences = (0 + 1 + 1 + 1 + 0 + 2 + 1 + 0) / 8
Absolute difference = 6 / 8 = 0.75
Learn more about mean absolute deviation at: https://brainly.com/question/447169
#SPJ1
Jefferson Middle School needs to see a 300% gain in PTO fundraiser
sales from last year. If they sold a total of $2,420 last year, how much do
they need to sell this year to meet their goal? *
Answers
Given parameters:
Percentage gain = 300%
Selling cost last year = $2420
Unknown:
Selling cost this year = ?
Solution:
To solve this problem;
Profit percent = \(\frac{Selling cost this year - Selling cost last year}{Selling cost last year} x 100\)
300 = \(\frac{S - 2420}{2420} x 100\)
3 = \(\frac{S - 2420}{2420}\)
S- 2420 = 7260
S = $9680
To make a 300% gain, Jefferson Middle school needs a $9680 from fundraiser sales this year.
Translate to an equation please.
four less than thirteen times a number is equal to that number added to eight
Answers
Hi
let call "a number" X.
then we have: 4-13X = X + 8 ..
13x-x = 8+ 4
12x= 12
X= 1
Find the perimeter of the figure to the right.
Answers
Answer: \(11a+16\) feet
Step-by-step explanation:
The perimeter is equal to the sum of the lengths of the sides.
\(2a+2a+2a+8+5a+8=11a+16\)
The equation a(s) = 37.5s - 1.5s2 models the function
represented in the table. Fill in the blank to complete the
restricted domain of the function. D = {0 ≤s ≤
Answers
The restricted domain of the function is 0≤s≤25
The equation is a(s) = 37.5s - 1.5s² models the function represented in the table
a(s) = s(37.5 - 1.5s)
The critical points are s=0 or
37.5 - 1.5s
37.5 = 1.5s
s=25
As area can not be negative, the area should be positive
s< 0 and s>25
Therefore, restricted domain is 0≤s≤25
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
I need help please and thank you 50 points and brain thing
Answers
Answer:
this is all correct btw love u baby
Step-by-step explanation:
a b c
<A opposite adjacent hypoth
<B adjacent opposite hypoth
Which answers I should have to answer
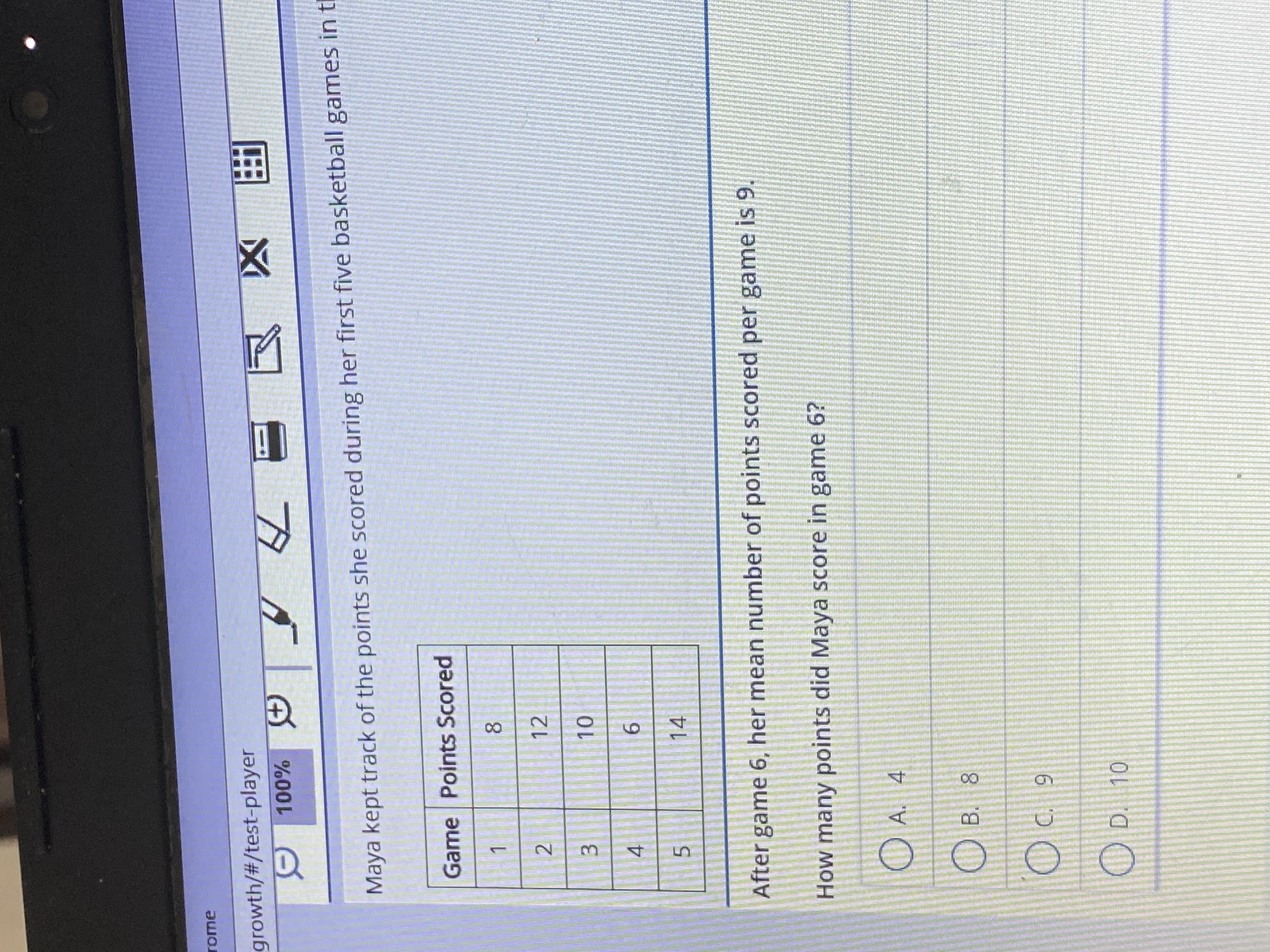
Answers
Given:
The table of point scored in 5 games.
After game 6, the mean number of points scored per game is 9.
To find:
The points scored by Maya in game 6.
Solution:
Let x be the points scored by Maya in game 6. Then sum of scores in all 6 games is:
\(Sum=8+12+10+6+14+x\)
\(Sum=50+x\)
We know that, the formula for mean is:
\(\text{Mean}=\dfrac{\text{Sum of all observations}}{\text{Total number of observations}}\)
So, the mean number of points scored per game is:
\(\text{Mean}=\dfrac{50+x}{6}\)
It is given that the mean number of points scored per game is 9.
\(\dfrac{50+x}{6}=9\)
\(50+x=9\times 6\)
\(x=54-50\)
\(x=4\)
Therefore, the correct option is A.
Is the following statement true or false? the mean of a random sample equals the mean of the population from which it was drawn.
Answers
The claim that the average of a random sample is the same as the average of the population from which it was taken is False.
Is the sample mean the same as the population mean?The sample mean will, of course, differ from the population means. The sample mean, however, is a fair estimation of the population mean if the sample is a simple random sample.
Thus, neither the sample mean nor the population mean is statistically greater or lower. The sample mean will always have a mean that is identical to the mean of the original non-normal distribution. In other words, the population mean is the same as the sample mean.
To know more about random samples click here: brainly.com/question/24466382
#SPJ4
PLEASE HELP
Given the following equation
f(x) = (x-1) / (x-2)^2 • (x+3), use the nine
steps to find an appropriate graph. (Domain, symmetry, 1st & 2nd
derivatives, possible CP's and IP's, increasing/decreasing, extreme
values & IP's, asymptotes & end behavior, intercepts, graph)
Answers
The vertical asymptotes are x=-3,2 and horizontal asymptotes is y=0.
The given function is f(x)=(x-1)/(x-2)²·(x+3).
What is the function?Functions are the fundamental part of the calculus in mathematics. The functions are the special types of relations. A function in math is visualized as a rule, which gives a unique output for every input x.
Find the asymptotes.
Vertical Asymptotes: x=-3,2
Horizontal Asymptotes: y=0
No Oblique Asymptotes
To find the x-intercept, substitute in 0 for y and solve for x. To find the y-intercept, substitute in 0 for x and solve for y.
x-intercept(s): (1,0)
y-intercept(s): (0,-1/12)
Therefore, the vertical asymptotes are x=-3,2 and horizontal asymptotes is y=0.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1
The original price of a dining table set is $400. The set is on sale for 40% off. What is the sale price of the set?
Answers
Answer:
Your answer will be $240
Can someone help me with this? A man purchased a used car for $1000. He decided t sell the car for 40% above his purchase price. He could not sell the car so he reduced his asking price by 40%. If he sells the car at the reduced price, will he have a profit or a loss or will he break even?
Answers
Answer:
He will be at a loss of $160
Explanation:
Here, we want to check if he can get the profit or loss
If the purchase price is $1000, 40% of this is $400, and that makes the initial asking price as $1,400
He was unable to sell and decide to reduce his asking price by 40%
That would be:
\(\begin{gathered} \text{ 40\% of \$1400 = \$560} \\ \text{New sales price would be:} \\ 1400-560\text{ = \$840} \end{gathered}\)The difference between the final sales price and the cost price will be:
\(840-1000\text{ = -\$160}\)What that simply means is that he will be at a loss of $160
2
Let g(x) = x + 4x-7.
What is g(x) in graphing form?
(x + 2) - 7 = 4
O g(x) = (x + 2)²-7
Onone of the answer choices
x² + 4x-7=0
O g(x) = (x + 2)² - 11
Answers
The graphing form of the function g(x) is: C) none of the answer choices.
The function g(x) = \(x^2 + 4x - 7\)is already in the standard form of a quadratic equation. In graphing form, a quadratic equation can be represented as y =\(ax^2 + bx + c,\) where a, b, and c are constants.
Comparing the given function g(x) =\(x^2 + 4x - 7\)with the standard form, we can identify the coefficients:
a = 1 (coefficient of x^2)
b = 4 (coefficient of x)
c = -7 (constant term)
Therefore, the graphing form of the function g(x) is:
C) none of the answer choices
None of the given answer choices (A, B, D, or E) accurately represents the graphing form of the function g(x) =\(x^2 + 4x - 7\). The function is already in the correct form, and there is no equivalent transformation provided in the answer choices. The given options either represent different equations or incorrect transformations of the original function.
In graphing form, the equation y = \(x^2 + 4x - 7\) represents a parabolic curve. The coefficient a determines the concavity of the curve, where a positive value (in this case, 1) indicates an upward-opening parabola.
The coefficients b and c affect the position of the vertex and the intercepts of the curve. To graph the function, one can plot points or use techniques such as completing the square or the quadratic formula to find the vertex and intercepts. Option C
For more such questions on graphing visit:
https://brainly.com/question/19040584
#SPJ8