Traveling at approximately 34,300 centimeters per
second, a sound wave would travel about how many
centimeters in 4 hours?
F. 4.94 x 108
G. 4.94 x 107
H. 8.23 x 106
J. 8.23 x 105
K 1.37 x 10
Answers
This is because if you convert 1 second to 4 hours:
1 x 60 x 60 x 4 = 14400
14400 x 34300 = 493920000
The decimal point has moved 8 spaces to the left therefore, it is F
Hope this helps! Any questions let me know :)
Related Questions
Write 5 +x= 3x2 in standard form.
An equation in standard form is
Answers
Answer:
Here's link to the answer:
...................
Step-by-step explanation:
i need help with this pls help pls show how you got it also

Answers
The range is from -3 to ∞
hile watching a car move down the street, you close your eyes and count off 15 seconds. When you open your eyes again, the car is 144 feet further down the road from when you last saw it.WHAT IF the car traveled at a constant speed while your eyes were closed - how fast would it have had to travel?a. What constant speed would allow the car to travel exactly 144 feet in exactly 15 seconds?Select an answer second ft/sec feetb. If a car traveled at this speed for tt seconds, what formula would model its distance dd (in feet) from the starting point in terms of the time elapsed, tt (in seconds)? Recall that this does not necessarilly represent the actual relationship between the distance traveled and time elapsed for the real car. This represents the relationship for an imaginary car traveling at a constant speed.s = d/t
Answers
Answer:
below
Step-by-step explanation:
A. To find the constant speed that allows the car to travel exactly 144 feet in exactly 15 seconds, we can use the formula: speed = distance / time.
So, speed = 144 feet / 15 seconds = 9.6 feet/second.
B. If a car traveled at a constant speed of 9.6 feet/second for t seconds, the formula for its distance dd (in feet) from the starting point in terms of the time elapsed, tt (in seconds) would be:
dd = 9.6 feet/second * t seconds = 9.6t feet.
Among the seven nominees for two vacancies on a city council are three men and four women. In how many ways can these vacancies be filled
Answers
This question is incomplete
Complete Question
Among the seven nominees for two vacancies on the city council are three men and four women. In how many ways may these vacancies be filled
a) with any two of the nominees?
b) with any two of the women?
c) with one of the men and one of the women?
Answer:
a) 21 ways
b) 6 ways
c) 12 ways
Step-by-step explanation:
We solve this question using combination formula
C(n, r) = nCr = n!/r! (n - r)!
a) with any two of the nominees?
Probability (two of the nominees) = 7C2
= 7!/2! ×(7 - 2)!
= 7!/ 2! × 5!
= 7 × 6 × 5 × 4 × 3 × 2 × 1/2 × 1 ×(5 × 4 × 3 × 2 × 1)
= 21
b) with any two of the women?
We have a total of 4 women
Hence, the probability of any two of the four women, filling the vacancies =
P(any two of the women) = 4C2
= 4!/2! ×( 4 - 2)!
= 4!/ 2! × 2!
= 4 × 3 × 2 × 1/ 2 × 1 ×( 2 × 1)
= 6
c) with one of the men and one of the
Total number of men = 3
Total number of women = 4
= 3C1 × 4C1
= [3!/1! ×(3 - 1)! ] × [4!/1! ×(4 - 1)! ]
= [3!/1! × 2!] × [4!/1! ×3!]
= [3 × 2 × 1/ 1 × 2 × 1] × [4 × 3 × 2 × 1/ 1 × 3 × 2 × 1]
= 3 × [24/6]
= 3 × 4
= 12 ways
The probability for any two of the nominees is 21
The probability for two women is 6
This question is incomplete
Complete Question
Among the seven nominees for two vacancies on the city council are three men and four women. In how many ways may these vacancies be filled
a) with any two of the nominees?
b) with any two of the women?
We have given,
Total number of nominees for two vacancy =7
We solve this question using combination formula
What is the formula for combination?
\(C(n, r) = nCr = n!/r! (n - r)!\)
a) with any two of the nominees?
Total number of nominees(n)=7
We are selecting r nominees r=2
Probability = 7C2
= \(\frac{7!}{2! (7 - 2)!}\)
= 7!/ 2! × 5!
= 21
b) with any two of the women?
We have a total number of women=4
Out of 4 we have select 2 women
Hence, the probability of any two of the four women is
4C2
= 4!/2! ×( 4 - 2)!
= 4!/ 2! × 2!
= 6
Therefore,probability for two women is 6
To learn more about the combination visit:
https://brainly.com/question/25821700
State the groups of shapes
Answers
Answer:
The groups are round shapes, triangles, quadrilaterals, pentagons, and hexagons.
Step-by-step explanation:
The groups are round shapes, triangles, quadrilaterals, pentagons, and hexagons.
find x please!!
a.10
b.32
c.116
d.16

Answers
9514 1404 393
Answer:
(d) 16
Step-by-step explanation:
Angles opposite sides of the same measure are congruent. Here, the triangle is isosceles, so the base angles are congruent:
2x = 32
x = 16 . . . . . . divide by 2°
Write and evaluate the definite integral that represents the area of the surface generated by revolving the curve on the indicated interval about the x-axis. (Round your answer to three decimal places.) y = 2 x 9 211 2V7 dx = 159.174 X x y = 2Vx 6 4 2 4. 6 8
Answers
Surface area generated by revolving the curve y = 2√(x) on the interval [4, 9] about the x-axis is approximately 159.174 square units.
What is Surface Area?The measurement of three-dimensional solids' surfaces the surfaces of three-dimensional solids, such as cubes, spheres, prisms, and pyramids, in square or meter units, is known as Surface area.
SA = \(\int\limits^ {} [a,b] 2\pi y\sqrt{(1+\frac{dy}{dx} )^{2}} dx\)
Given, y = 2√(x)
\(\frac{dy}{dx}\) = \(\frac{1}{\sqrt{(x)} }\)
\(SA =\int\limits^ {} [4,9] 2\pi \sqrt{2(x)} \sqrt{(1+\frac{1}{\sqrt{(x)} } )^{2}} dx\)
\(SA = 4\pi \int\limits\ [4,9]\sqrt{(x^{2}+x)} dx\)
To solve this integral, we use the substitution u = x² + x:
We get, dx = du/(2x + 1)
When x = 4, u = 20, and when x = 9, u = 90, so the limits of integration become [20, 90]:
\(SA = 4\pi \int\limits[20,90]\sqrt{u\ \frac{du}{(2x + 1)} }\)
\(SA = 2\pi \int\limits[20,90]u^{\frac{1}{2} } (2x + 1)^{\frac{-1}{2} } du\)
Using the power rule of integration in the above equation, we get:
SA = 2π [(2/3)(90 + 90^(3/2)) - (2/3)(20 + 20^(3/2))]
SA = 2π (120 - 4√5)
SA ≈ 159.174
Therefore, surface area generated by revolving the curve y = 2√(x) on the interval [4, 9] about the x-axis is approximately 159.174 square units.
To learn more about surface area, visit:
https://brainly.com/question/951562
#SPJ1
Jenny is 5 feet, 3
inches tall. Naomi is
64 inches tall. Who
is shorter?
Answers
Answer:
Naomi is smaller
Step-by-step explanation:
Hope I could help!
God bless you.Have a great day!!
What’s the correct answer for this question?

Answers
Answer: choice A 1/2
Step-by-step explanation:
Events A and B are independent if the equation P(A∩B) = P(A) · P(B) holds true.
so
1/3=2/3*p(B)
p(B)=1/2
Do the first 15 Questions With work shown
Answers
Answer:
ching chong
Step-by-step explanation:
What value of x satisfies the conclusion of the mean value theorem for f(x) = ln(x3) over the interval [1, e2]?
Answers
Answer:
\(x \approx 3.195\) satisfies the conclusion of the Mean Value Theorem for \(f(x) = \ln x^{3}\) over the interval \([1,e^{2}]\).
Step-by-step explanation:
According to the Mean Value Theorem, for all function that is differentiable over the interval \([a, b]\), there is at a value \(c\) within the interval such that:
\(f'(c) = \frac{f(b)-f(a)}{b-a}\) (1)
Where:
\(a\), \(b\) - Lower and upper bounds.
\(f(a)\), \(f(b)\) - Function evaluated at lower and upper bounds.
\(f'(c)\) - First derivative of the function evaluated at \(c\).
If we know that \(f(x) = \ln x^{3} = 3\cdot \ln x\), \(f'(x) = \frac{3}{x}\), \(a = 1\) and \(b = e^{2}\), then we find that:
\(\frac{3}{c} = \frac{3\cdot \ln e^{2}-3\cdot \ln 1}{e^{2}-1}\)
\(\frac{3}{c} = \frac{6\cdot \ln e-3\cdot \ln 1 }{e^{2}-1 }\)
\(\frac{3}{c} = \frac{6}{e^{2}-1}\)
\(c = \frac{1}{2}\cdot (e^{2}-1)\)
\(c \approx 3.195\)
\(x \approx 3.195\) satisfies the conclusion of the Mean Value Theorem for \(f(x) = \ln x^{3}\) over the interval \([1,e^{2}]\).
Answer:
C. 1/2(e^2-1)
Step-by-step explanation:
Edge AP Cal 2022
Can someone please help me with 5 and 6 like rnnn please???

Answers
Answer:
6 is 140°
step by step
same line meant that the angle abc equals 180°
so DBC =180-40=140° .
Which of the following equations is not linear?
Y= -8
Y= 2x to the power of 2
Y= 9x
Y= x + 6
Answers
Answer:
the second one
Step-by-step explanation:since i helped can i have brainlist please :D
Given the sequence 1/2 ; 4 ; 1/4 ; 7 ; 1/8 ; 10;.. calculate the sum of 50 terms
Answers
Hint :-
Break the given sequence into two parts .Notice the terms at gap of one term beginning from the first term .They are like \(\dfrac{1}{2},\dfrac{1}{4},\dfrac{1}{8}\) . Next term is obtained by multiplying half to the previous term . Notice the terms beginning from 2nd term , \(4,7,10,13\) . Next term is obtained by adding 3 to the previous term .Solution :-
We need to find out the sum of 50 terms of the given sequence . After splitting the given sequence ,
\(\implies S_1 = \dfrac{1}{2},\dfrac{1}{4},\dfrac{1}{8}\) .
We can see that this is in Geometric Progression where 1/2 is the common ratio . Calculating the sum of 25 terms , we have ,
\(\implies S_1 = a\dfrac{1-r^n}{1-r} \\\\\implies S_1 = \dfrac{1}{2}\left[ \dfrac{1-\bigg(\dfrac{1}{2}\bigg)^{25}}{1-\dfrac{1}{2}}\right] \)
Notice the term \(\dfrac{1}{2^{25}}\) will be too small , so we can neglect it and take its approximation as 0 .
\(\implies S_1\approx \cancel{ \dfrac{1}{2} } \left[ \dfrac{1-0}{\cancel{\dfrac{1}{2} }}\right] \)
\(\\\implies \boxed{ S_1 \approx 1 }\)
\(\rule{200}2\)
Now the second sequence is in Arithmetic Progression , with common difference = 3 .
\(\implies S_2=\dfrac{n}{2}[2a + (n-1)d] \)
Substitute ,
\(\implies S_2=\dfrac{25}{2}[2(4) + (25-1)3] =\boxed{ 908} \)
Hence sum = 908 + 1 = 909
Help and explain
Don’t use for points or I will take it back
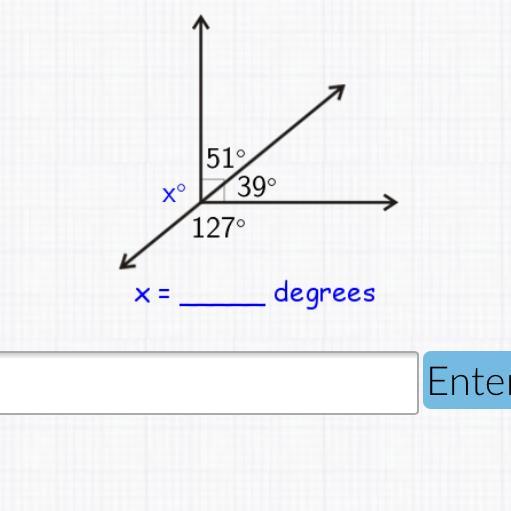
Answers
Step-by-step explanation:
step 1. x + 51 + 39 + 127 = 360 (1 revolution is 360°)
step 2. x + 90 + 127 = 360
step 3. x + 127 = 270. (subtract 90 on both sides)
step 4. x = 143° (subtract 127 on both sides)
⚠️URGENT PLS HELP
LINKS WILL BE REPORTED

Answers
Answer:
e and c
Step-by-step explanation:
2x -20 = -30
What is x?
Answers
2x-20=-30
x-10=-15
+10 +10
x=-5
Explanation: first, you need to divide by 2 to both sides. then, add 10 to both sides.
You should get, x=-5.
Complete the proof of the identity by choosing the Rule that justifies each step.
(1- cos x) so
secx sin tan
To see a detailed description of a Rule, select the More Information Button to the right of the Rule,

Answers
( 1 - cos²x ) secx
=> sin²x . secx
Here the rule ( rule 1 ) is the first trigonometric identity [ sin²A + cos²A = 1 ] by simplifying we have , [ 1 - cos²A = sin² ] . So here we substituted 1 - cos²x = sin²x .
=> sin²x [ 1/cosx ]
Here the rule ( rule 2 ) is secx = 1/cosx . So here we substituted secx = 1/cosx .
=> sinx [ sinx/cosx ]
Here the rule ( rule 3 ) is sin²x can be written as sinx . sinx , so we get sinx . sinx [ 1/cosx ] next by simplifying , sinx [ sinx/cosx ].
=> sinx tanx
Here the rule ( rule 4 ) is , in the above we got sinx/cosx and here we know that , sinx/cosx = tanx . So we have tan x .
The proof of the identity that justifies that ( 1 - cos²x ) secx equals sinx(tanx) has been described below with statements and rules.
Statement 1; ( 1 - cos²x ) secx
This is given
Statement 2; sin²x · secx
Rule 1; From trigonometric identities, we know that;
sin²x + cos²x = 1,
Thus; cos²x = 1 - sin²x
Thus; ( 1 - cos²x ) secx = sin²x · secx
Statement 3; sin²x (1/cosx)
Rule 2; The rule here according to trigionometric identities is that; secx = 1/cosx. Thus; secx = 1/cosx .
Statement 4; sinx (sinx/cosx )
Rule 3; The rule here is that sin²x can be expressed as (sinx * sinx)
Thus, we have; sinx . sinx (1/cosx) = sinx (sinx/cosx ).
Statement 5; sinx(tanx)
Rule 4; The rule here is that; sinx/cosx = tanx.
Thus; sinx (sinx/cosx ) gives us sinx(tanx)
Read more at; https://brainly.com/question/24836845
Help me please, thank you

Answers
Answer:
Option D is your correct answer
I think it will help.
The price of chocolates increased from $12.99
per pound to $14.99 per pound. What is the
percent
increase? Round to the nearest tenth of
a percent.
Answers
Answer:
About 13.3 percent
To find the percent increase divide 12.99 by 14.99 and get .8666577 subtract one to find percent increase and get .13342228 turn into percent and round to the nearest tenths place and get - 13.3 percent.
how to determine standard deviation of discrete random variables when given standard deviation and mena
Answers
To calculate the standard deviation of discrete random variables when given standard deviation and mean, we can follow the mentioned procedure.
Determine the mean, or expected value, by adding the products of each result and its probability:
μ = n ∑ i = 1
x 1p1 + x2p2 + xnpn = x I p I
Step 2: Using the formula
σ^2=n∑i=1,
calculate the variance for the random variable.
p I ( x I − μ ) 2 .
Step 3: Take the square root of the variance to calculate the standard deviation.
A discrete random variable is one that can have just a finite number of or countably infinitely many different values. However, this does not mean that the sample space can only have a finite number of outcomes.
A random variable is one that can have several values, each of which has a certain probability of occuring. The random variable is discrete when there are a finite (or countable) number of such values.
Random variables are distinct from "regular" variables, which have a fixed (but frequently unknown) value.
To learn more about discrete random variables
brainly.com/question/17238189
#SPJ4
What is 150% of 60?
Select one:
90
30
9
40
Answers
Answer: 90
Step-by-step explanation:
If you do the following:
100% of 60 = 60
50% of 60 = 30
60 + 30 = 90
What is the slope of the line represented by the values in the table ?

Answers
Answer:
2
Step-by-step explanation:
14-(-2)/10-2
14+2/10-2
16/8
2
A circle has a circumference of 12. t has an arc of length 8/5. What is the central angle of the arc, in degrees?
Answers
Answer:45.9
Step-by-step explanation:
Circumference=12
Length of arc=8/5=1.6
π=3.14
Circumference=2 x π x r
12=2x3.14xr
12=6.28 x r
Divide both sides by 6.28
12/6.28=(6.28 x r)/6.28
2=r
r=2
Length of arc =Φ/360 x 2 x π x r
1.6=Φ/360 x 2 x 3.14 x 2
1.6=(Φ x 2 x 3.14 x2)/360
1.6=12.56Φ/360
Cross multiply
1.6x360=12.56Φ
576=12.56Φ
Divide both sides by 12.56
576/12.56=12.56Φ/12.56
45.9=Φ
Φ=45.9
Mrs. Phillips ordered 56 sub sandwiches for a team meal, and 2/7 of them were ham. how many of the sandwiches were ham?
Answers
Answer:
16
Step-by-step explanation:
Take the total number of sandwiches and multiply the fraction that were ham
56 * 2/7
56/7 *2
8 *2
16
16 sandwiches were ham
center =
3. A diameter of a circle has endpoints P(-7,-4) and Q (3,2).
a. Find the center of the circle (hint use midpoint formula)
b. Find the radius. If your answer is not and integer, express in radical form. (hint use
distance formula)
c. Write an equation for the circle.
17
radius=
equation of the circle:
work:
< 2/3
I
>
Answers
a. The center of the circle is (-2, -1).
b. The radius of the circle is √136.
c. The equation of the circle is (x + 2)^2 + (y + 1)^2 = 136.
a. To find the center of the circle, we can use the midpoint formula, which states that the midpoint of a line segment with endpoints (x1, y1) and (x2, y2) is given by:
Midpoint = ((x1 + x2)/2, (y1 + y2)/2)
In this case, the endpoints of the diameter are P(-7, -4) and Q(3, 2).Applying the midpoint formula:
Midpoint = ((-7 + 3)/2, (-4 + 2)/2)
= (-4/2, -2/2)
= (-2, -1)
Therefore, the center of the circle is at the coordinates (-2, -1).
b. To find the radius of the circle, we can use the distance formula, which calculates the distance between two points (x1, y1) and (x2, y2). The radius of the circle is half the length of the diameter, which is the distance between points P and Q.
Distance = √\([(x2 - x1)^2 + (y2 - y1)^2]\)
Using the distance formula:
Distance = √[(3 - (-7))^2 + (2 - (-4))^2]
= √\([(3 + 7)^2 + (2 + 4)^2]\)
= √\([10^2 + 6^2\)]
= √[100 + 36]
= √136
Therefore, the radius of the circle is √136.
c. The equation for a circle with center (h, k) and radius r is given by:
\((x - h)^2 + (y - k)^2 = r^2\)
In this case, the center of the circle is (-2, -1), and the radius is √136. Substituting these values into the equation:
\((x - (-2))^2 + (y - (-1))^2\) = (√\(136)^2\)
\((x + 2)^2 + (y + 1)^2 = 136\)
Therefore, the equation of the circle is (x + 2)^2 + (y + 1)^2 = 136.
For more such questions on center visit:
https://brainly.com/question/30396931
#SPJ8
What is the solution when the equation y=4x+13 is evaluated at x = 4
Answers
Answer:
29
Step-by-step explanation:
If x = 4, then y = 4x + 13 can be written as the following:
y = 4(4) + 13
y = 16 + 13
y = 29
Hope this helps!
-6 - (-8) x 5 ÷ (-10)
Answers
Answer:
- 10
Step-by-step explanation:
-6+8×5÷-10
-6+40÷-10
-6-4
-10
Answer and Step-by-step explanation:
According to PEMDAS (Parenthesis, Exponents, Multiplication, Division, Addition, Subtraction),
First we multiply, then divide, then finally add/subtract.
-8 times 5 is -40.
-40 divided by -10 is 4.
-6 - 4 = -10
The answer to the expression is -10.
#teamtrees #PAW (Plant And Water)
Alan is building a garden shaped like a rectangle with a semicircle attached to one short side. If he has 70 feet of fencing to go around it, what dimensions will give him the maximum area in the garden? Round the answers to the nearest tenth.
Answers
The dimension that would give the maximum area is 20.8569
How to solve for the maximum area
Let the shorter side be = x
Perimeter of the semi-circle is πx
Twice the Length of the longer side
\([70-(\pi )x -x]\)
Length = \([70-(1+\pi )x]/2\)
Total area =
area of rectangle + area of the semi-circle.
Total area =
\(x[[70-(1+\pi )x]/2] + [(\pi )(x/2)^2]/2\)
When we square it we would have
\(70x +[(\pi /4)-(1+\pi)]x^2\)
This gives
\(70x - [3.3562]x^2\)
From here we divide by 2
\(35x - 1.6781x^2\)
The maximum side would be at
\(x = 35/2*1.6781\)
This gives us 20.8569
Read more on areas and dimensions here:
https://brainly.com/question/19819849
#SPJ1
6. The mean of 5 consecutive integers is 19. What is the difference between the largest and
the smallest of the 5 integers?
Answers
Answer:
4
Step-by-step explanation:
The integers are
x
x+1
x+2
x+3
x+4
since they are consecutive
The largest is x+4
The smallest is x
Difference is
x+4 -x
4
Answer:
Step-by-step explanation:
If the least integer is n, it means the five consecutive integers are:
n,n+1,n+2,n+3,n+4
Summing all integers we have:
n + n+1+n+2+n+3+n+4
=5n+10
The mean of this integers is
5n+10 /5 =19
5n+10=19*5
5n + 10 = 95
5n = 95 - 10
5n =85
n=85/5=17
The smallest of the integer is n= 17
The largest integer is n + 4 =17+4=23
The difference between the least and largest integer would be;
Is 4
The sum of largest integer and the smallest integer is 23 + 17 = 40