This graph represents a linear relationship between x and y. Which equation best represents the relationship shown in this graph? y=35x y=−53x y=53x y=−35x

Answers
Answer:
y= 5/3x
Step-by-step explanation:
Answer:
D
Step-by-step explanation:
i took the test and it gave me the answer.

Related Questions
Joel has a goal to practice his clarinet for 4 1/2 hours per week. The list below shows the number of hours Joel has practiced so far this week.
Monday: 1 1\2 hours
Wednesday: 1 1\4 hours
Thursday: 1 hour
How many more hours does Joel need to practice this week to meet his goal?
Answers
Answer: 3/4 hour
Step-by-step explanation: Add them all to get 3 3/4. subtract that from 4 1/2.
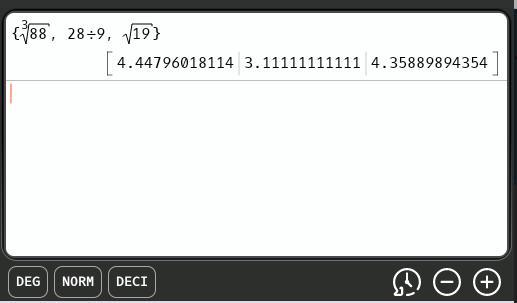
Order cube root of eighty-eight, twenty-eight ninths, square root of nineteen from greatest to least.
cube root of eighty-eight, twenty-eight ninths, square root of nineteen
twenty-eight ninths, square root of nineteen, cube root of eighty-eight
twenty-eight ninths, cube root of eighty-eight, square root of nineteen
cube root of eighty-eight, square root of nineteen, twenty-eight ninths
Answers
Answer:
(a) twenty-eight ninths, square root of nineteen, cube root of eighty-eight
Step-by-step explanation:
When ordering a list of numbers by hand, it is convenient to convert them to the same form. Decimal equivalents are easily found using a calculator.
OrderThe attachment shows the ordering, least to greatest, to be ...
\(\dfrac{28}{9}.\ \sqrt{19},\ \sqrt[3]{88}\)
__
Additional comment
We know that √19 > √16 = 4, and ∛88 > ∛64 = 4, so the fraction 28/9 will be the smallest. That leaves us to compare √19 and ∛88, both of which are near the same value between 4 and 5.
One way to do the comparison is to convert these to values that need to have the same root:
√19 = 19^(1/2) = 19^(3/6) = sixthroot(19³)
∛88 = 88^(1/3) = 88^(2/6) = sixthroot(88²)
The roots will have the same ordering as 19³ and 88².
Of course, these values can be found easily using a calculator, as can the original roots. By hand, we might compute them as ...
19³ = (20 -1)³ = 20³ -3(20²) +3(20) -1 = 8000 -1200 +60 -1 = 6859
88² = (90 -2)² = 90² -2(2)(90) +2² = 8100 -360 +4 = 7744
Then the ordering is ...
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Answer:
the ordering is
28/9 < 19³ < 88² ⇒ 28/9 < √19 < ∛88
Step-by-step explanation:
i am confused on finding the answer i have tried a few times and i do not understand

Answers
Answer:
Volume = 7.912
Step-by-step explanation:
V = πr²h
V = 3.14 × 3/4 × 3/4 × 6 3/4 ( π = 22/7 or 3.14 )
V = 3.14 × 9/16 ×18/4
V = 3.14 × 0.56 × 4.5
V = 7.912
Image shows an isosceles triangle.
The perimeter of this isosceles triangle is 22 cm. If one side is 6 cm, what are the possible lengths of the other two sides?
Explain how you know. Provide at least one reason for your answer
Answers
option 1 is 6, 6, and 10 cm
Option 2 is 6, 8 and 8 cm
An isosceles triangle has two sides that are congruent, and a third side not congruent.
Perimeter given is 22 cm.
Explanation
Option 1, we have given side 6, so the other congruent side would also be 6. Your perimeter is 22. 22 - 6 - 6 = 10 for third side
Option 2, we have given side 6, so the other two sides will have to be congruent.
22 - 6 = 16. Divide 16 by 2 equal sides = 8 and 8 for the other two sides.
2/7 = 4/5 + 1/7 q answe for q
Answers
Answer:
??
Step-by-step explanation:
Answer:
what
Step-by-step explanation:
I need help with this question

Answers
Answer:
check online for more information
NO LINKS!! URGENT HELP!!
Calculate the perimeter of the following figures.

Answers
Answer:
Quadrilateral: 20.5 units
Triangle: 8.6 units
Step-by-step explanation:
Quadrilateral:
We can use the following formula to find the perimeter of a quadrilateral.
Perimeter = AB + BC + CD + DA
where AB, BC, CD, and DA are the lengths of the four sides of the quadrilateral.
In your case, the coordinates of the vertices of the quadrilateral are A(-3,-1), B(-3,3), C(2,3), and D(4,-1).
Using the distance formula, we can find the lengths of the four sides of the quadrilateral as follows:
\(AB = \sqrt{(-3 - (-3))^2 + ((-1) - 3)^2} = \sqrt{16} = 4\)
\(BC = \sqrt{(-3 - 2)^2 + ((3) - 3)^2} = \sqrt{25}= 5\)
\(CD = \sqrt{(2 - 4)^2 + ((3) - (-1))^2} = \sqrt{4+16} = 2\sqrt{5}\)
\(DA = \sqrt{(4 - (-3))^2 + ((-1) - 1)^2} = \sqrt{49} =7\)
Therefore, the perimeter of the quadrilateral is:
Perimeter = AB + BC + CD + DA
= \(4+5+2\sqrt5+7=20.5\) units
Triangle
The perimeter of a triangle is the total length of all three sides of the triangle. To find the perimeter of a triangle, we can use the following formula:
Perimeter = AB + BC + CA
where AB, BC, and CA are the lengths of the three sides of the triangle.
In your case, the coordinates of the vertices of the triangle are
E(-4,1), F(-2,3), and G(-2,4). Using the distance formula, we can find the lengths of the three sides of the triangle as follows:
\(EF = \sqrt{(-4 - (-2))^2 + ((1) - (3))^2} = 2\sqrt{2}\)
\(FG = \sqrt{(-2 - (-2))^2 + ((3) - (4))^2} = 1\)
\(EG = \sqrt{(-4 - (-2))^2 + ((1) - (4))^2} = \sqrt{4 + 9} = \sqrt{13}\)
Therefore, the perimeter of the triangle is:
Perimeter = EF + FG + EG
= 4 + 1 + \(\sqrt{13}\)
=8.6 units
Therefore, the perimeter of the quadrilateral is 20.5 units and the perimeter of the triangle is 8.6 units


8. The first three terms of a geometric sequence are ( x-6), 3x, and y. If the common ratio is 6, then the value of y is.
Answers
Answer:
The value of y is 216
(and the value of x is 12)
Step-by-step explanation:
The general formula for a geometric sequence is,
\(a_n = a_1(r)^{n-1}\)
Where n represents the nth term, a_1 is the first term and r is the common ratio,
we see that,
r = 6,
the first term is,
a_1 = (x-6)
the 2nd term is,
a_2 = 3x,
the 3rd term is,
a_3 = y, finding y,
first we find x, using the above given formula we have,
\(a_2 = a_1(6)^{2-1}\\3x = (x-6)(6^1)\\3x = 6x -36\\36 = 6x - 3x\\36 = 3x\\x=36/3\\x=12\)
x = 12,
Now, for y we can use the relation between a_3 and a_2,
\(a_3 = a_1(6)^{3-1}\\y = (x-6)(6)^2\\y = (12-6)(6^2)\\y = 6(6^2)\\y = 6^3\\y = 216\)
y = 216
What is the equation of this line?
y= 2x - 3
y= -1/2x- 3
y= -2x - 3
y= 1/2x - 3

Answers
Answer:
First option) y= 2x - 3
Step-by-step explanation:
[] The y-intercept, our b, is -3. This does not rule out any of the options as they all have -3.
[] The slope, when we have a graph with clear points, can be found with rise-over-run. We will pick a point and then count up and over to the next point.
-> Starting at the y-intercept, (0, 3), we count up 2 and to the right 1 for a slope of 2/1. This simplifies to 2.
[] Our equation is y = 2x - 3
Have a nice day!
I hope this is what you are looking for, but if not - comment! I will edit and update my answer accordingly.
- Heather

Please help me with this.

Answers
Here are the correct matches to the expressions to their solutions.
The GCF of 28 and 60 is 4.
(-3/8)+(-5/8) = -4/4 = -1.
-1/6 DIVIDED BY 1/2 = -1/6 X 2 = -1/3.
The solution of 0.5 x = -1 is x = -2.
The solution of 1/2 m = 0 is m = 0.
-4 + 5/3 = -11/3.
-2 1/3 - 4 2/3 = -10/3.
4 is not a solution of -4 < x.
1. The GCF of 28 and 60 is 4.
The greatest common factor (GCF) of two numbers is the largest number that is a factor of both numbers. To find the GCF of 28 and 60, we can factor each number completely:
28 = 2 x 2 x 7
60 = 2 x 2 x 3 x 5
The factors that are common to both numbers are 2 and 2. The GCF of 28 and 60 is 2 x 2 = 4.
2. (-3/8)+(-5/8) = -1.
To add two fractions, we need to have a common denominator. The common denominator of 8/8 and 5/8 is 8. So, (-3/8)+(-5/8) = (-3 + (-5))/8 = -8/8 = -1.
3. -1/6 DIVIDED BY 1/2 = -1/3.
To divide by a fraction, we can multiply by the reciprocal of the fraction. The reciprocal of 1/2 is 2/1. So, -1/6 DIVIDED BY 1/2 = -1/6 x 2/1 = -2/6 = -1/3.
4. The solution of 0.5 x = -1 is x = -2.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate x by dividing both sides of the equation by 0.5. This gives us x = -1 / 0.5 = -2.
5. The solution of 1 m = 0 is m = 0.
To solve an equation, we can isolate the variable on one side of the equation and then solve for the variable. In this case, we can isolate m by dividing both sides of the equation by 1. This gives us m = 0 / 1 = 0.
6. -4 + 5/3 = -11/3.
To add a fraction and a whole number, we can convert the whole number to a fraction with the same denominator as the fraction. In this case, we can convert -4 to -4/3. So, -4 + 5/3 = -4/3 + 5/3 = -11/3.
7. -2 1/3 - 4 2/3 = -10/3.
To subtract two fractions, we need to have a common denominator. The common denominator of 1/3 and 2/3 is 3. So, -2 1/3 - 4 2/3 = (-2 + (-4))/3 = -6/3 = -10/3.
8. 4 is not a solution of -4 < x.
The inequality -4 < x means that x must be greater than -4. The number 4 is not greater than -4, so it is not a solution of the inequality.
For more such questions on GCF
https://brainly.com/question/902408
#SPJ8
Which of the following describes graphing y ≥ |x| - 4? A. Translate y = |x| down 4 units and shade inside the V. B. Translate y = |x| right 4 units and shade inside the V. C. Translate y = |x| left 4 units and shade inside the V. D. Translate y = |x| up 4 units and shade inside the V.
Answers
To graph y = |x| - 4, we can start by plotting the points where x = 0, x = -1, and x = 1:
When x = 0, y = |0| - 4 = -4, so the point (0, -4) is on the graph.
When x = -1, y = |-1| - 4 = -3, so the point (-1, -3) is on the graph.
When x = 1, y = |1| - 4 = -3, so the point (1, -3) is on the graph.
Plotting these points and connecting them with a V-shaped curve, we get the graph of y = |x| - 4.
To shade the region above or on the graph of y = |x| - 4, we can shade the inside of the V-shaped curve.
Therefore, the correct answer is A. Translate y = |x| down 4 units and shade inside the V.
The lines y=-2 and y=-7 are they parallel, perpendicular, or neither?
Answers
Answer:
parallel
Step-by-step explanation:
An equation of the form
y = k
where k is a number is a horizontal line.
Since both lines have the form y = k, with two different values of k, -2 and -7, these are two different horizontal lines, so they are parallel.
Answer: parallel
Answer:
Parallel -inf to inf
Step-by-step explanation:
there is no x value so they never cross
I need help on this problem please?

Answers
Answer:
yes ur friend is correct
Step-by-step explanation:
because the value of x .
The diagram only shows that angles M and B are supplementary ( add up to 180 degrees) and that angel 4x is adjacent to angel M.However, there is no information about the measure of angle B or angel M, so we cannot determine the value of x
If x=1/2 and y=3/2, find the values of i) xy÷(x+y) ii) x+y ÷ x-y
Answers
Answer:
i) 3/8
ii) -2
Step-by-step explanation:
i) 1/2*3/2/(1/2+3/2)
3/4/2
3/4*1/2
3/8.
ii) 1/2+3/2 / 1/3-3/2
2/-1
-2.
Hope this helps :)
i need help i also put a screenshot

Answers
Answer:
6.2
Step-by-step explanation:
every minute 6.2 gallons fill into the pool.
the 7th term of a Gp is 192 and it common ratio is 2 find the first term
Answers
\(n^{th}\textit{ term of a geometric sequence} \\\\ a_n=a_1\cdot r^{n-1}\qquad \begin{cases} a_7=\stackrel{7^{th}\ term}{192}\\ 7=\textit{term position}\\ a_1=\textit{first term}\\ r=\stackrel{\textit{common ratio}}{2} \end{cases} \qquad \qquad a_7=a_1\cdot 2^{7-1} \\\\\\ 192=a_1\cdot 2^6 \implies 192=64a_1\implies \cfrac{192}{64}=a_1\implies \boxed{3=a_1}\)
Sammie pays $30 for a bag that she buys at a discount of 50% . what is the price of the bag without the discount
Answers
Answer:
$60
Step-by-step explanation:
30 ÷ 0.50 = 60
Please answer this correctly without making mistakes

Answers
Answer:
The second answer is correct
Step-by-step explanation:
1, 3, and 6 are proportional to 5/3, 5, and 10
I hope this helps you :)
What the answer to 7+8=
Answers
(even if it’s a joke I want points)
Aaliyah has x nickels and y pennies. She has a minimum of 20 coins worth no more than $0.40 combined. Solve this system of inequalities graphically and determine one possible solution.
Answers
Answer:
\((x,y) = (5,15)\)
Step-by-step explanation:
Given
\(Nickels = x\)
\(Pennies = y\)
Minimum of 20 coins means:
\(x + y \ge 20\)
A nickel worth $0.05
A penny worth $0.01
So, the worth can be represented as:
\(0.05x + 0.01y \le 0.40\)
See attachment for graph
From the attachment, the solution is:
\((x,y) = (5,15)\)
A study was conducted on the educational level of patients with AIDS, it was asume that
with ten years of education will be in group A, between 10 and 20 group B and between 20
group C. After the analysis it was realized that group A had 100 persons while group B and C had 30 persons
(a) If you decide to select based on proportion of 10% from each group how many patien
selected from each group. Show your calculation.
(b) What name can be given to the classified groups?
(c) What method of sampling was employed in the selection process?
1. State and explain the three major data collection techniques.
What is a variable?
What is a Parameter?
Answers
A variable is a characteristic or attribute that can take on different values. It is an observable and measurable property of an object or phenomenon, which can be used to describe and analyze it.
Parameters are used in inferential statistics to make conclusions about a population based on a sample of data.
(a) If you decide to select based on proportion of 10% from each group, the number of patients selected from each group would be: Group A = (10/100) x 100 = 10 patients Group B = (10/100) x 30 = 3 patients Group C = (10/100) x 30 = 3 patients.
(b) The classified groups can be named as follows: Group A = 10 years of education or less Group B = More than 10 years but less than or equal to 20 years of education Group C = More than 20 years of education.
(c) The sampling method employed in the selection process was stratified sampling. Stratified sampling is a type of probability sampling technique where the population is divided into homogeneous subgroups or strata, and the researcher selects a simple random sample from each subgroup or stratum.
The researcher chooses a proportion of participants from each subgroup to represent the population as a whole, which allows for more precise estimates of the population parameters than simple random sampling.
The sample is selected randomly from the stratified sample, which ensures that the sample is representative of the population.
A variable is a characteristic or attribute that can take on different values. It is an observable and measurable property of an object or phenomenon, which can be used to describe and analyze it.
Variables are used in research to test hypotheses, determine relationships between different phenomena, and make predictions about future outcomes.
A parameter is a numerical summary of a population, which describes a characteristic of the population. It is an unknown constant that can only be estimated from a sample of data.
Parameters are used in inferential statistics to make conclusions about a population based on a sample of data.
For more such questions on Parameters
https://brainly.com/question/29673432
#SPJ8
no the projvet iS 348
3=20
14. Model Real Life A self-balancing scooter travels 12 miles
per hour. An all-terrain vehicle can travel 6 times as
fast as the scooter. A go-kart can travel 67 miles
per hour. Which vehicle can travel the fastest?
Answers
An all-terrain vehicle can travel the fastest.
What is Speed ?Speed can be define as the time rate by which an object is moving or running along a path. A speed is the quantity which describes the moving rate of any object. We can define the speed with respect to distance and time . Or we can say speed is distance per unit of time . It is calculate in term of kilometers per hour.
Mathematically, we can write:
\(Speed = \frac{Distance}{Time}\)
where, distance is measured in km
and Time is measured in hours
In the question, the distance for three different types of vehicles are given and we have to find fastest vehicle for which we need to find the speed.
For self-balancing scooter
Time = 1 hour
Distance = 12 miles
Therefore, Speed = 12 miles/h
For all-terrain vehicle
Time = 1 hour
Distance = 12 . 6 = 72 miles
Therefore, speed = 72 miles/h
For a go-kart
Time = 1 hour
Distance = 67 miles
Therefore, speed = 67 miles/h
Hence it is cleared that An all-terrain vehicle can travel the fastest.
To know more about speed and distance, visit:
brainly.com/question/18242918
#SPJ9
In the Gaussian integral, how does the left side of this equation equal the right side? An answer would be really appreciated, thank you.

Answers
the left side of this equation equal the right side through the process of completing the square that establishes the equality between the left side and the right side of the Gaussian integral equation.
How do we calculate?
using completing the square method:
Starting with the left side of the equation:
∫\(e^(^-^x^2)\) dx
\(e^(^-^x^2) = (e^(^-x^2/2))^2\)
∫\((e^(^-^x^2/2))^2 dx\)
let u = √(x²/2) = x = √(2u²).
dx = √2u du.
∫ \((e^(^x^2/2))^2 dx\)
= ∫ \((e^(^-2u^2)\)) (√2u du)
The integral of \(e^(-2u^2)\)= √(π/2).
∫ \((e^(-x^2/2))^2\) dx
= ∫ (√2u du) \((e^(-2u^2))\\\)
= √(π/2) ∫ (√2u du)
We substitute back u = √(x²/2), we obtain:
∫ \((e^(-x^2/2))^2\)dx
= √(π/2) (√(x²/2))²
= √(π/2) (x²/2)
= (√π/2) x²
A comparison with the right side of the equation shows that they are are equal.
Learn more about Gaussian integral equation at:
https://brainly.com/question/33550421
#SPJ1
Calc II Question
Find the volume of the solid obtained by rotating the region bonded bt the given curves about the specified line.
Y = In x
Y = 1
Y = 2
X = 0
About the Y axis
Answers
Work attached in image. Since the solid is being rotated about the y-axis, you would need to solve y=lnx in terms of x. The rest of the process is showed in the image.

Write an equation of a line that contains the following two points in slope intercept form
(-2,4) (3,-1)
Answers
Answer:
y = -x + 2
Step-by-step explanation:
The slope intercept form equation of this line can be written like this :
y = my + p ; where m is the slope and p is the y intercept.
\(m = \frac{-1-4}{3-(-2)} = \frac{-5}{5} =-1\)
then the equation becomes y = -x + p
(-2,4) is a point of the line means 4 = -(-2) + p
then p = 4 - 2 = 2
finally, y = -x + 2
You get hangry so you go to In-n-Out. You buy burgers for $3.45 and one milkshake for $2.30. Your bill is $16.10 before tax. Write and solve an equation to find the number of burgers you eat.
Define your variable: n = number of burgers you eat
Answers
Formulate:
2.3 + 3.45 × x = 16.1
Solve the equation:
2.3 + 3.45x = 16.1
Rearrange variables to the left side of the equation:
3.45x = 16.1 - 2.3
Calculate the sum or difference:
3.45x = 13.8
Divide both sides of the equation by the coefficient of variable:
x = ¹³·⁸/₃.₄₅
Multiply both the numerator and denominator with the same integer
x = ¹³⁸⁰/₃₄₅
Cross out the common factor:
x = 4
AA.1 Solutions to inequalities P9N
Which of the following are solutions to the inequality below? Select all that apply.
3 ≤ 47
x = 24
Submit
x = 51
X = 6
X = 99
Answers
Answer: 3 ≤ 47
Step-by-step explanation:
The inequality given is 3 ≤ 47.
To determine the solutions to this inequality, we need to find the values of x that satisfy the inequality.
Looking at the options provided:
x = 24: This is not a solution because 24 is less than 47.
x = 51: This is a solution because 51 is greater than or equal to 47.
x = 6: This is not a solution because 6 is less than 47.
x = 99: This is a solution because 99 is greater than or equal to 47.
Therefore, the solutions to the inequality 3 ≤ 47 are x = 51 and x = 99.
The table and graph both represent the same relationship. which equation also represents that relationship?

Answers
Answer:
I think it's y= 2x
Step-by-step explanation:
For every number in y, x increases by 2
Answer:
y=x2
Step-by-step explanation:
The first one because 2x2 is 4 .
4x2 is 8
6x2 is 12
At birth, a newborn baby's head is about 25% of its total length. If a baby's head is 4.5 inches long, how many total inches is the baby?
Answers
Answer:
1.125 inches
Step-by-step explanation:
25 percent of 4.5
Answer:
give oliver brainliest
Step-by-step explanation: rainnn
A hot dog stand sells hot dogs for $3 each, but each hot dog costs $1.50 to make. Each month, the hot dog stand pays $800 in rent and $1,200 in employee wages. If the hot dog stand sells 3,120 hot dogs in a month, how much will the hot dog stand earn in profit?
Answers
Answer:
$2680
Step-by-step explanation:
3.00-1.50= 1.50 profit per hotdog
1200+800=2000 expenses
1.50 (3120) = 4680
4680-2000=
2680 in profit