Answers
Answer:
D. y = x - 4
Step-by-step explanation:
Given the following data;
Points (x, y) = (3, -1)
To find the equation of line;
First of all, we would determine the slope of the graph.
Mathematically, slope is given by the formula;
\( Slope = \frac{Change \; in \; y \; axis}{Change \; in \; x \; axis} \)
\( Slope, m = \frac {y_{2} - y_{1}}{x_{2} - x_{1}} \)
Substituting into the equation, we have;
\( Slope, m = \frac {5 - 5}{5 - 5} \)
Slope, m = 1
Generally, the equation of straight line is y = mx + c
Where;
m is the slope.
x and y are the points
c is the intercept.
Substituting the values in order to find the intercept, we have;
Using points (x, y) = (3, -1)
-1 = 1*3 + c
-1 = 3 + c
c = -1 - 3
Intercept, c = -4
Therefore, the equation of line becomes;
y = x - 4.
Related Questions
Can anybody help me on the question.
ASAP

Answers
The hanger in the illustration will have the value x = 6, and it will remain balanced.
Define equations?Mathematical expressions with two algebraic expressions on either side of the equals (=) sign are called equations. It demonstrates the equality of the expressions printed on the left and right sides. We have LHS = RHS (left hand side = right hand side) in each mathematical equation. To determine the value of an unknown variable that stands in for an unknown quantity, equations can be solved.
Here's the query,
Considering the graph,
The hanger's equation is as follows:
4x= 24
There are 4 numbers here that represent the value of the hanger.
So, x+x+x+x will be 24.
The equation is thus:
4x = 24.
Now, by resolving the equation, we can determine the value of x that balances the hanger:
4x = 24.
When you divide 4 on both sides:
x = 24/4
x = 6.
As a result, the hanger will remain in equilibrium for x = 6.
To know more about equations, visit:
brainly.com/question/29657983
#SPJ1
A fish tank holds 175 gallons of water. Tom is emptying the tank and
removes 25 gallons per hour. Write an equation to model the situation,
where x represents time in hours and y represents the number of gallons
of water in the fish tank.
Answers
How many times larger is 9 x 10^4 than 3 x 10^2?
Answers
Answer: \(300\) \(times\)
Step-by-step explanation:
Match the type of graph with its description.

Answers
Answer:
1) Compares data that are in categories
2) Organises data into 4 groups of equal sizes and is often used to compare two sets of data.
3) Used to see trends in data.
4) Shows changes over time.
5) Shows the frequency of data using equal intervals with no space between the bars.
Step-by-step explanation:
1) Bar graph is used to compare data that are in categories
2) Box and whisker plot is used to organise data into 4 groups of equal size.
3) Line graph is basically used to see different trends.
4) Scatter plot is used to show changes that have occurred over time
5) Histogram is used to show the frequency of data using equal intervals with no space between the bars.
Solve for x.
3(x + 2) + 4(x - 5) = 10
Answers
Step-by-step explanation:
3x+6+4x-20=10
7x-14=10
7x=24
x=24/7
Answer:
x=3.43
Step-by-step explanation:
3(x-2)+4(x-5)=10
3x+6+4x-20=10
7x-14=10
7x=24
x=24/7
24/7=3.428571428571429(round to nearest hundredths)
x=3.43
Find the output, y, when the input, x, is -9.
y =

Answers
Answer:
when x=-9, y=1
Step-by-step explanation:
the graph shows when the x is at -9, the y is at 1

Explain the difference between an indefinite integral and a definite integral.
A) An indefinite integral, after evaluating it at the limits of integration, results in a particular number. A definite integral results in a set of functions that share the same derivative and uses an arbitrary constant of integration.
B) A definite integral, after evaluating it at the limits of integration, results in a particular number. An indefinite integral results in a set of functions that share the same derivative and uses an arbitrary constant of integration.
C) An indefinte integral cannot always be integrated analytically and may require numeric integration, while it is always possible to integrate a definite integral. Definite integrals always return a real number after evaluation at its limits of integration.
D) A definite integral is defined and continuous over the interval of integration and has finite limits of integration. An indefinite integral is also defined and continuous over the interval of integration, but may have as a limit of integration.
Answers
The answer is A.
An indefinite integral is a function that, when differentiated, equals the original function. It is denoted by ∫f(x)dx, where f(x) is the function to be integrated. An indefinite integral always has an arbitrary constant of integration, which is denoted by C. This is because the derivative of any constant is zero, so the derivative of ∫f(x)dx+C is still equal to f(x).
A definite integral is the limit of a Riemann sum as the number of terms tends to infinity. It is denoted by ∫
a
b
f(x)dx, where a and b are the limits of integration. A definite integral does not have an arbitrary constant of integration, because the limits of integration specify a unique value for the integral.
In other words, an indefinite integral is a family of functions that share the same derivative, while a definite integral is a single number.
x^2+12x−7=(x+p)^2−q. find the value of p and the value of q
Answers
Answer:
p = 6 , q = 43
Step-by-step explanation:
x² + 12x - 7
using the method of completing the square
add/subtract ( half the coefficient of the x- term )² to x² + 12x
=x² + 2(6)x + 36 - 36 - 7
= (x + 6)² - 43 ← in the form (x + p)² - q
with p = 6 and q = 43
The triangles below are similar.
Which similarity statement expresses the relationship between the two triangles?
FGH~KLJ
FGH=KLJ
FGH~JKL
FGH=JKL

Answers
Answer:
Option (1)
Step-by-step explanation:
Triangles given are the similar triangles.
In the given triangles ΔFGH and ΔKLJ,
m∠G = m∠L = 65°
m∠H = m∠J = 24°
m∠F = m∠K = 91°
Since all three interior angles are equal in measure,
Therefore, ΔFGH and ΔKLJ are similar.
ΔFGH ~ ΔKLJ
Option (1) is the correct option.
Answer:
A. FGH ~ KLJ
Step-by-step explanation:
I took the test.
50 Points! Multiple choice geometry question. Photo attached. Thank you!

Answers
5/6 is the probability that the number landed on an odd or is greater than 4
Probability conceptProbability is defined as the likelihood or chance that an event will occur.
If a number cube is rolled, the sample space will be:
(S) = {1, 2, 3, 4, 5, 6}
n(S) = 67
If it lands on a odd number, the number of events will be:
(E) = {1, 3, 5}
n(E) = 3
If it lands on a number greater than 4 the number of events will be:
(E) = {5, 6}
n(E) = 2
Pr(even or greater then 4) = 3/6 + 2/6
Pr(even or greater then 4) = 5/6
The probability that the number landed on an odd or is greater than 4 is 5/6
Learn more on probability here: https://brainly.com/question/24756209
#SPJ1
Answer: 4/6 or 2/3
Step-by-step explanation:
Even number=3/6 or 1/2 chance
Greater than 4=2/6 chance or 1/3 chance
Union basically means either or
So: 1/2+1/3 or 3/6+2/6 or 5/6
This doesn't always work though, so we use trial and error
1 2 3 4 5 6
1 3 5 are the ones not even
13 are the ones not greater than 4
solve for h
can someone please answer and explain thank you <33

Answers
Answer: \(h=\frac{2A}{(a+b)}\)
Step-by-step explanation:
To solve for h, we want to get h alone. We need to use our algebraic properties.
\(A=\frac{1}{2} h(a+b)\) [multiply both sides by 2]
\(2A=h(a+b)\) [divide both sides by (a+b)]
\(h=\frac{2A}{(a+b)}\)
Now that we have h alone, we know that \(h=\frac{2A}{(a+b)}\).
Which equation can be used to determine the distance between the origin and (–2, –4)? d = StartRoot ((0 minus 2) + (0 minus 4)) squared EndRoot d = StartRoot (0 minus (negative 2)) squared + (0 minus (negative 4)) squared EndRoot d = StartRoot ((0 minus 2) minus (0 minus 4)) squared EndRoot d = StartRoot (0 minus (negative 2)) squared minus (0 minus (negative 4)) squared EndRoot
Answers
Answer:person up top is right it’s B
Step-by-step explanation: on edg 2020
Answer:
The answer is B
Step-by-step explanation:
lol yw guys
This Venn diagram shows sports played by 10 students.
Karl
Jada
Gabby
PLAYS
BASKETBALL
O A=0.50
OB. 0.29
OC. =0.40
D.
=0.20
Fran
Juan
lan
Ella
Let event A = The student plays basketball.
Let event B = The student plays soccer.
What is P(AB)?
PLAYS
SOCCER
Mickey
Mai
Marcus
Answers
The conditional probability for this problem is given as follows:
C. P(A|B) = 2/5 = 0.4 = 40%.
How to calculate a probability?The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes.
For this problem, we have that 5 students play soccer, and of those, 2 play basketball, hence the conditional probability is given as follows:
C. P(A|B) = 2/5 = 0.4 = 40%.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1

Find the first 8 multiples of 92
Answers
Answer:
92, 184, 276, 368, 460, 552, 644, 736, 828, 920
Step-by-step explanation:
hope this helps :D
brainliest appreciated
PLEASEEEE HURRYY
On Giana's map of Texas, there is a close up view of the Dallas/Fort Worth area. The map scale is 1 inch = 3.5 miles. From Garland to Mansfield is 52.5 miles. How far apart are these two cities on the map?
Answers
Answer:
The distance between Garland and Mansfield on the map is 15 inches.
Step-by-step explanation:
On Giana's map of Texas, the scale is 1 inch = 3.5 miles. To determine the distance between Garland and Mansfield on the map, we can use the scale to find the corresponding measurement. Given that the actual distance between these two cities is 52.5 miles, we can set up a proportion:
1 inch / 3.5 miles = x inches / 52.5 miles
Cross-multiplying, we have:
3.5 miles * x inches = 1 inch * 52.5 miles
3.5x = 52.5
Dividing both sides by 3.5, we find:
x = 15
Therefore, the distance between Garland and Mansfield on the map is 15 inches.
For more questions on distance
https://brainly.com/question/28342342
#SPJ11
A local charity collected 163 cans of food
every day for 14 days. How many did they
collect in the first 10 days? How many did
they collect in the remaining 4 days? How
many cans did they collect in all? Solve this
problem any way you choose,
Answers
163 x 10 to find how many they collected in 10 days, which is 1630.
And in the remaining four days you would do
163 x 4 which is 652.
And in order to find the total amount of cans they collected it is
1630 + 652 which is 2282.
What is the gradient of the blue line
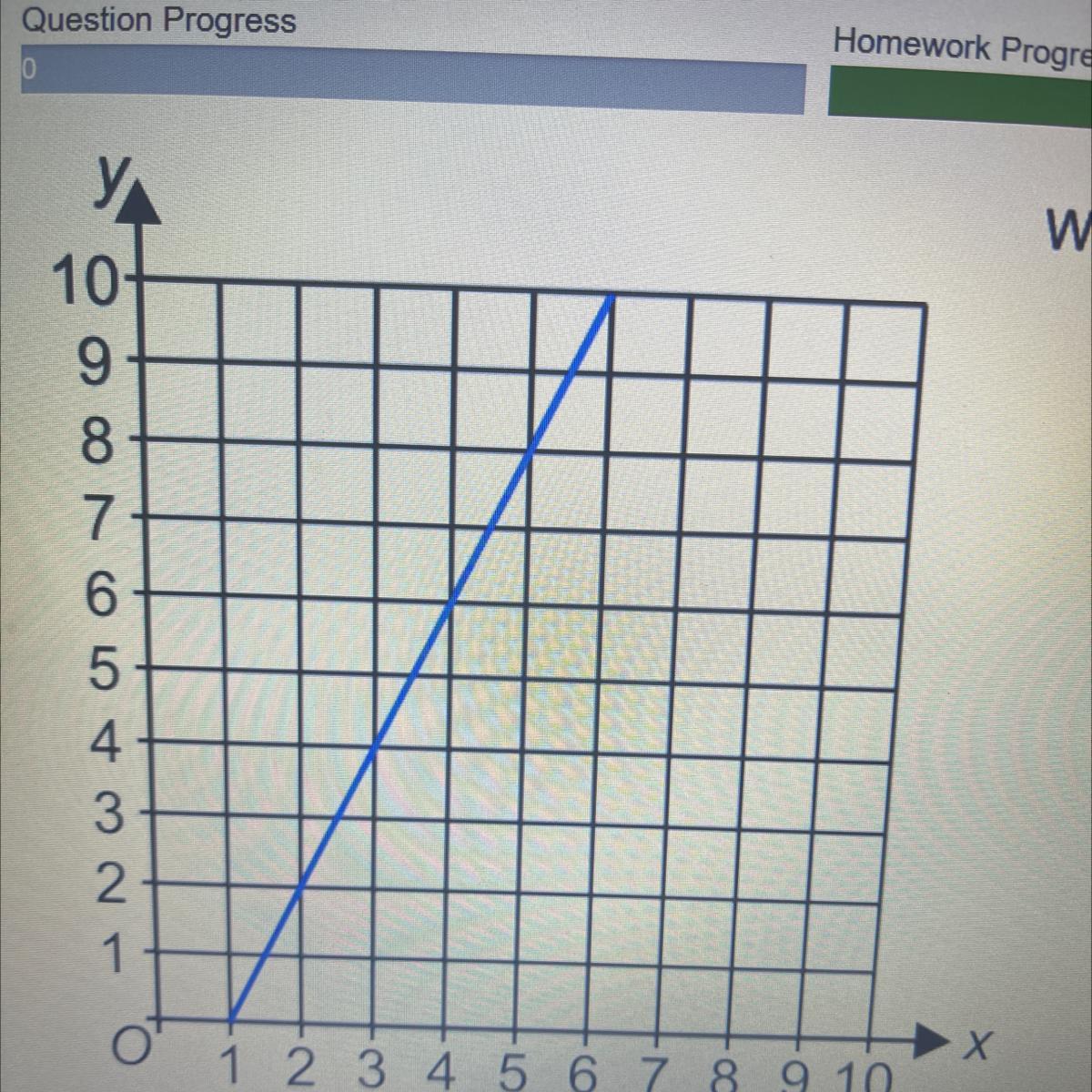
Answers
Answer:
Up 2 to the right 1
Step-by-step explanation:
that would be i think
(3 x 8) x 4 = 3 x (O)
Answers
Answer:
(O)=32 us the answer to the question.
Is an integer less than its opposite
Answers
Answer:
An integer can be negative or positive, so if the integer is, let's say, -6. The opposite, or absolute value, of -6, is 6. So in this case, the opposite has more value than the actual integer. Does that answer the question? :D
Answer:
No
Step-by-step explanation:
I am assuming the "opposite" is its reciprocal
If an integer is negative ex: -2, then its reciprocal: -1/2 is larger.
Find the exact value of sin A in simplest radical form.
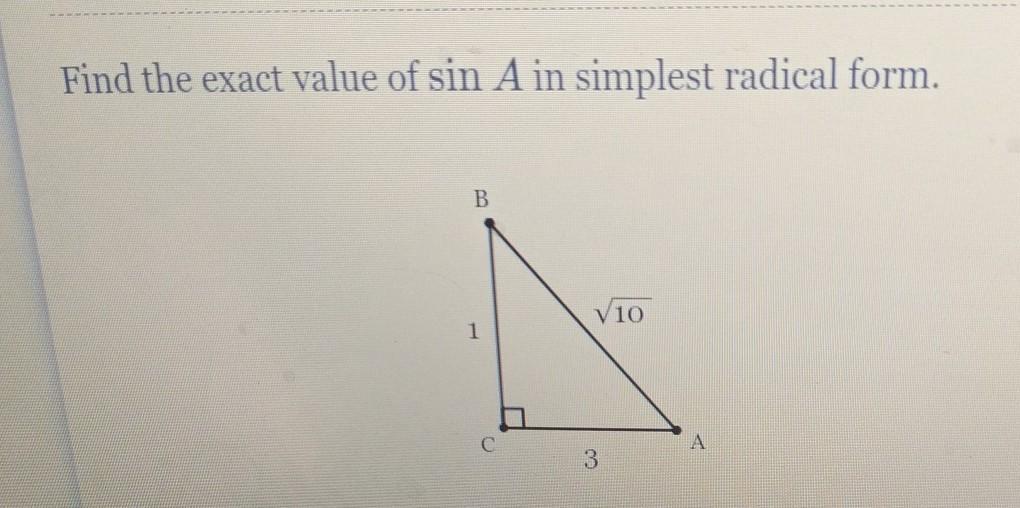
Answers
Answer:
✓10/10
Step-by-step explanation:
sinA = 1/✓10
Rationalize the denominator by multiplying by ✓10:
sinA = 1✓10/✓10✓10
sinA = ✓10/10
Elements that do not belong to a set belong to its
Answers
Answer:
What do you mean for this question?
Step-by-step explanation:
Give specific details
Aaron works at a furniture store. He sells a table that normally costs $670 but is on sale
for 15% off. If he makes 8% commission on
the sale price, how much will he make in
commission?
Answers
Answer :$45.56
Self explanation:
Evaluate log4 exponent 0.5
Answers
We can claim that after answering the above question, the So, logarithm \(log4 (0.5^(1/2)) =-0.0752\)
what is logarithm?The logarithm is a power's reciprocal in mathematics. Accordingly, the exponent by which b must be raised to obtain a number x equals the logarithm of that number in base b. For instance, since 1000 = 103, its base-10 logarithm is 3, or log10 = 3. As an illustration, the base 10 logarithm of 10 is 2, while the square of 10 is 100. Log 100 = 2. To answer a question like, For example, how many times must a base of 10 be multiplied by itself to achieve 1,000, a logarithm (or log) is the mathematical term utilized. The solution is 3 (1,000 = 10 10 10).
Using the following property of logarithms:
\(log_a (b^c) = c * log_a (b)\\log4 (0.5^(1/2))\\(1/2) * log4 (0.5)\\log4 (0.5) = log (0.5) / log (4)\\log (0.5) ≈ -0.3010\\log (4) = 2\)
Therefore,
\(log4 (0.5) ≈ -0.3010 / 2 ≈ -0.1505\\(1/2) * log4 (0.5) ≈ (1/2) * (-0.1505) ≈ -0.0752\\\)
So, \(log4 (0.5^(1/2)) =-0.0752\)
To know more about logarithm visit:
https://brainly.com/question/30085872
#SPJ1
It is estimated that approximately 8.23% Americans are afflicted with diabetes. Suppose that a certain diagnostic evaluation for diabetes will correctly diagnose 98% of all adults over with diabetes as having the disease and incorrectly diagnoses 3.5% of all adults over without diabetes as having the disease.
a) Find the probability that a randomly selected adult over does not have diabetes, and is diagnosed as having diabetes (such diagnoses are called "false positives").
b) Find the probability that a randomly selected adult of is diagnosed as not having diabetes.
c) Find the probability that a randomly selected adult over actually has diabetes, given that he/she is diagnosed as not having diabetes
Answers
The probabilities in this problem are given as follows:
a) False positive: 0.0321 = 3.21%.
b) Diagnosed as not having diabetes: 0.8872 = 88.72%.
c) Actually has diabetes, if diagnosed as not having: 0.0019 = 0.19%.
What is Conditional Probability?Conditional probability is the probability of one event happening, considering a previous event. The formula is given as follows:
\(P(B|A) = \frac{P(A \cap B)}{P(A)}\)
In which the parameters are described as follows:
P(B|A) is the probability of event B happening, given that event A happened.\(P(A \cap B)\) is the probability of both events A and B happening.P(A) is the probability of event A happening.For item a, we have that:
100 - 8.23 = 91.77% of the people do not have diabetes.Of those, 3.5% are diagnosed with diabetes.Hence the probability of a false positive is given as follows:
p = 0.9177 x 0.035 = 0.0321 = 3.21%.
For item b, the percentage of people who is not diagnosed as having diabetes is divided as:
96.5% of 91.77% (do not have diabetes).2% of 8.23% (have diabetes).Hence the probability is:
P(A) = 0.965 x 0.9177 + 0.02 x 0.0823 = 0.8872 = 88.72%.
For item c, we find the conditional probability, as follows:
\(P(A \cap B) = 0.02 \times 0.0823 = 0.001646\)
Then:
P(B|A) = 0.001646/0.8872 = 0.0019 = 0.19%.
More can be learned about probabilities at https://brainly.com/question/14398287
#SPJ1
how to convert 90% to a decimal point
Answers
Answer:
0.90
Step-by-step explanation:
Just like a decimal to a percentage number, you must multiply by 100. By converting a percentage number to a decimal point, you must divide it by 100. Which means, the decimal must move 2 times.
For example,
0.90 x 100 = 90%
This is decimal to percentage number, but in this case it is percentage to decimal.
90%.
Since the number ended at 0, put the decimal there and move it 2 times to get to your decimal point.
.90 = 0.90
There you'll get your answer! ^^
90% = 0.90
Right triangle with a hypotenuse of 159 ft and Angle A = 34 degree
Calculate the length of the sides they should be rounded to the nearest whole foot. The rounded for the legs (side) should be used to calculate the area of the triangle
Answers
the length of side a is 91 ft (rounded to the nearest whole foot) and the length of side b is 132 ft (rounded to the nearest whole foot). The area of the triangle is approximately 6007 sq ft.
Given: The hypotenuse of the right triangle,
c = 159 ft; angle A = 34°
We know that, in a right-angled triangle:
\($$\sin\theta=\frac{\text{opposite}}\)
\({\text{hypotenuse}}$$$$\cos\theta=\frac{\text{adjacent}}\)
\({\text{hypotenuse}}$$\)
We know the value of the hypotenuse and angle A. Using trigonometric ratios, we can find the length of sides in the right triangle.We will use the following formulas:
\($$\sin\theta=\frac{\text{opposite}}\)
\({\text{hypotenuse}}$$$$\cos\theta=\frac{\text{adjacent}}\)
\({\text{hypotenuse}}$$$$\tan\theta=\frac{\text{opposite}}\)
\({\text{adjacent}}$$\) Length of side a is:
\($$\begin{aligned} \sin A &=\frac{a}{c}\\ a &=c \sin A\\ &= 159\sin 34°\\ &= 91.4 \text{ ft} \end{aligned}$$Length of side b is:$$\begin{aligned} \cos A &=\frac{b}{c}\\ b &=c \cos A\\ &= 159\cos 34°\\ &= 131.5 \text{ ft} \end{aligned}$$\)
Now, we have the values of all sides of the right triangle. We can calculate the area of the triangle by using the formula for the area of a right triangle:
\($$\text{Area} = \frac{1}{2}ab$$\)
Putting the values of a and b:
\($$\begin{aligned} \text{Area} &=\frac{1}{2}ab\\ &=\frac{1}{2}(91.4)(131.5)\\ &= 6006.55 \approx 6007 \text{ sq ft}\end{aligned}$$\)
Therefore, the length of side a is 91 ft (rounded to the nearest whole foot) and the length of side b is 132 ft (rounded to the nearest whole foot). The area of the triangle is approximately 6007 sq ft.
For more question triangle
https://brainly.com/question/29135702
#SPJ8
Mercedes is helmet diving at a location of -20 feet. The breathing tube attached to her helmet reaches an oxygen tank at a location of 12 feet.
Which of the following expressions represents
the length, in feet, of the breathing tube attached
to Mercedes' helmet?
(A) |--20 – 12
(B) |--20 + 12
(C) 20 – 12
(D) -20 + 12
Answers
Answer: B
Step-by-step explanation:
The Weaver family went to dinner and spent $52.75. They had great service so they tipped the server 22%. What was the Weaver's total bill?
Answers
To find the total amount that the Weaver family spent on their dinner, you need to add the tip to the original bill. To calculate the tip, you need to multiply the cost of the dinner by the percentage of the tip: $52.75 × 22% = $11.61.
Then, you can add the tip to the original bill to find the total cost of the dinner: $52.75 + $11.61 = $64.36.
Therefore, the Weaver family's total bill for their dinner was $64.36.
Simplify show step by step 30 POINTS!

Answers
Step-by-step explanation:
hopefully it makes sense and is visible
:)

Analyze the diagram below and complete the instructions that follow.
8
45°
Find the value of x.
A. 4
B. 8√√2
2
C. 4√2
DG
45°
Save and Exit
Next
Subr

Answers
Answer:
Based on the diagram, we can see that the triangle formed by the line segment with length 8 and the two dashed line segments is a right triangle with a 45° angle. This means that the other two angles of the triangle are also 45° each.
Using the properties of 45°-45°-90° triangles, we know that the length of the hypotenuse is equal to the length of either leg times the square root of 2. Therefore, we have:
x = 8 / sqrt(2) = 8 * sqrt(2) / 2 = 4 * sqrt(2)
So the value of x is option B: 8√2 / 2 or simplified, 4√2.
