The inverse of the function y = 22 +3 is y = –20 – 3
True
False
Answers
Answer:
true
Step-by-step explanation:
Answer:
False
Step-by-step explanation:
Related Questions
devin is skip counting. 5, 10, 15, 20, 25, 30, 35. What rule does this pattern follow?
Answers
Answer:
he is skip counting by 5s
Step-by-step explanation:
Answer: the rule is +5
Step-by-step explanation: 5+5=10 10+5=15 15+5=20 20+5=25 25+5=30 30+5=35
Regular hexagon ABCDEF is inscribed in a circle with center H. What is the image of segment BC after 120 degree clockwise rotation about point H?
Answers
Regular hexagon ABCDEF is inscribed in a circle with center H, the image of segment BC after 120 degree clockwise rotation about point H is the segment joining the points B' and C', which has endpoints (-0.5r\(\sqrt{3\), -0.5r) and (-0.5r, -0.5r).
Since the hexagon is inscribed in a circle with center H, we can conclude that H is also the center of the circle passing through vertices B, C, and D. Therefore, the circle passing through B, C, and D is also a 120 degree clockwise rotation of the circle passing through A, B, and C.
To find the image of segment BC after a 120 degree clockwise rotation about point H, we need to find the coordinates of B and C relative to H, and then apply a 120 degree rotation matrix to these coordinates.
Let the radius of the circle be r, and let the coordinates of H be (0,0). Then the coordinates of B and C are:
B: (r cos(60), r sin(60))
C: (r cos(0), r sin(0)) = (r, 0)
To apply a 120 degree clockwise rotation matrix, we can use the following matrix:
[ cos(-120) -sin(-120) ]
[ sin(-120) cos(-120) ]
Simplifying, we get:
[ cos(120) sin(120) ]
[ -sin(120) cos(120) ]
Applying this matrix to the coordinates of B and C, we get:
B': [ cos(120) sin(120) ][ r cos(60) ] = [ -0.5r \(\sqrt{3}\)]
[ -sin(120) cos(120) ][ r sin(60) ] [ -0.5r ]
C': [ cos(120) sin(120) ][ r ] = [ -0.5r ]
[ -sin(120) cos(120) ][ 0 ] [ -0.5r ]
Therefore, the image of segment BC after a 120 degree clockwise rotation about point H is the segment joining points B' and C', which has endpoints (-0.5r\(\sqrt{3}\), -0.5r) and (-0.5r, -0.5r), respectively.
To know more about Hexagon:
https://brainly.com/question/2001860
#SPJ4
which of the following are geometric sequences?
a: 5,10,20,40,80,160
b: 3,6,9,12,15,18
c: 10,5,2.5,1.25,0.625,0.3125
d:1,3,9,27,81
Answers
Answer:
A, C, D
Step-by-step explanation:
This is because the ratio between te consecutive terms are constant, that is ×2, ×0.5 and ×3 respectively
what does the convolution method theorem say? when is it
useful?
Answers
The convolution method theorem states that convolution in the time domain is equivalent to multiplication in the frequency domain.
The convolution method theorem states that the convolution of two signals in the time domain is equivalent to the multiplication of their Fourier transforms in the frequency domain.
This theorem is useful in signal processing and mathematics as it allows us to analyze and manipulate signals using the simpler operations of multiplication and addition in the frequency domain rather than convolution in the time domain.
By transforming signals into the frequency domain, we can take advantage of the properties of the Fourier transform, such as linearity and the convolution theorem, to simplify and solve complex mathematical operations.
In practical terms, the convolution method theorem finds applications in various areas, including image processing, audio and speech processing, communication systems, and digital signal processing.
It enables us to perform operations like filtering, deconvolution, modulation, and system analysis more efficiently.
By leveraging the convolution method theorem, engineers and scientists can develop algorithms and techniques to enhance and extract meaningful information from signals, leading to advancements in fields such as image recognition, audio compression, and wireless communications.
learn more about convolution method here:
https://brainly.com/question/33223622
#SPJ11
Two interacting populations of hares and foxes can be modeled by the recursive equations:h(t+1)=4h(t)-2f(t)f(h+1)=h(t)+f(t)For each of the initial populations given in parts (a) through (c), find closed formulas for h(t) and f(t).a. h(0)=f(0)=100b. h(0)=200, f(0)=100c. h(0)=600, f(0)=500
Answers
The closed formula of h(t) and f(t) for
h(0)=f(0)=100b => h(t) = 100(2t+1), f(t) = 100(2t-1) ,
h(0)=200, f(0)=100 => h(t) = 200(2t+1), f(t) = 100(2t-1)
h(0)=600, f(0)=500 =>h(t) = 300 + 200(2t+\((-1)^{t}\)), f(t) = 200 - 100\((-1)^{t}\)
The recursive equations for the given two interacting population of hares and foxes are
h(t+1)=4h(t)-2f(t)
f(h+1)=h(t)+f(t)
for the given initial population in parts from a to c we need to create a close formula for h(t) and f(t)
where h(0) = f(0) =100h(t) = 100(2t+1)
f(t) = 100(2t-1)
where h(0) = 200, f(0) =100h(t) = 200(2t+1)
f(t) = 100(2t-1)
where h(0) = 600, f(0) = 500h(t) = 300 + 200(2t+\((-1)^{t}\))
f(t) = 200 - 100\((-1)^{t}\)
The closed formula of h(t) and f(t) for
h(0)=f(0)=100b => h(t) = 100(2t+1), f(t) = 100(2t-1) ,
h(0)=200, f(0)=100 => h(t) = 200(2t+1), f(t) = 100(2t-1)
h(0)=600, f(0)=500 =>h(t) = 300 + 200(2t+\((-1)^{t}\)), f(t) = 200 - 100\((-1)^{t}\)
To learn more about recursive equations,
https://brainly.com/question/29224065
#SPJ4
The expression
³√x²y³ = x²y³
where x and y are non-negative real numbers.
r, the exponent of X, is:
s, the exponent of y, is:
Answers
Using exponent power property, ³√x²y³ = x^r y^s, where x and y are non-negative real numbers.
r, the exponent of x, is: 2/3
s, the exponent of y, is: 1
What is Exponent power property?According to the Power of a Power Property, you can multiply the exponents if one exponent is increased to a higher exponent. This characteristic may be used to resolve the equation (3 x 2) 3.
³√x²y³ = x^r y^s
Cubing on both sides,
x²y³ = x^3r y^3s
As base is same, equating the powers
⇒ 2 = 3r; r = 2/3
⇒ 3 = 3s; s = 1
The correct question is -The expression
³√x²y³ = x^ry^s
where x and y are non-negative real numbers.
r, the exponent of X, is:
s, the exponent of y, is:
To learn more about exponent power property from given link
https://brainly.com/question/3187898
#SPJ9
Guess my favorite movie for brainliest no hints 50 points and brainliest to who gets it but only the first two people to guess are the contestants
Answers
Answer:
planet of the apes?
A gardener is planting two types of trees: Type A is 5 feet tall and grows at a rate of 4 inches per year. Type B is 2 feet tall and grows at a rate of 10 inches per year. Algebraically determine exactly how many years it will take for these trees to be the same height.
Answers
It will take 18 years for the Type A and Type B trees to be the same height.
What is the midpoint formula?A location in the centre of a line connecting two places is referred to as the midpoint. The midpoint of a line is located between the two reference points, which are its ends. The line that connects these two places is split in half equally at the halfway. In addition, the halfway is reached if a line is drawn to divide the line that connects these two places.
Let us suppose the number of years = y.
The height of the tree of type A is thus,
5 feet + (4 inches/year)(y)
= 5 + 4/12 y feet
= 5 + 1/3 y feet
For the type B:
2 feet + (10 inches/year)(y years)
= 2 + 10/12 y feet
= 2 + 5/6 y feet
To get the height of the two trees as equal we have:
5 + 1/3 y = 2 + 5/6 y
3 + 1/3 y = 5/6 y
3 = 1/6 y
18 = y
Hence, it will take 18 years for the Type A and Type B trees to be the same height.
Learn more about midpoint formula here:
https://brainly.com/question/30242987
#SPJ1
Find the value of m and YZ if Y is between X and Z.

Answers
Step-by-step explanation:
we know that xy+yz=xz
so if we fill in what we know
5m+1m=25
solve from there
a local restaurant purchased 10 pounds of flour at a total cost of $40. what is the cost for one pound of flour?
Answers
Answer:
4 dollars a pound
Step-by-step explanation:
4x 10 = 40
9. assume that a vowel is one of the five letters a, e, i, o, or u. (a) how many eleven-letter sequences from the alphabet contain exactly three vowels? (b) how many of these have at least one repeated letter?
Answers
(a) The total number of eleven-letter sequences with exactly three vowels are 318,937,572,165.
(b) The number of sequences with at least one repeated letter is 318,937,572,165 - C(26, 11).
(a) To find the number of eleven-letter sequences with exactly three vowels, we need to consider the placement of the vowels and consonants separately.
There are 5 vowels (a, e, i, o, u) and 21 consonants in the alphabet.
First, let's choose the positions for the 3 vowels. We can do this in C(11, 3) = 165 ways, where C(n, r) represents the number of combinations of choosing r items from a set of n items without considering the order.
Next, we need to fill the remaining 8 positions with consonants. There are 21 consonants to choose from, and we have 8 positions to fill. So, the number of ways to do this is 21^8.
To find the total number of eleven-letter sequences with exactly three vowels, we multiply these two results: 165 * 21^8 = 318,937,572,165.
(b) Now, let's find the number of these sequences that have at least one repeated letter.
We can use the principle of inclusion-exclusion to solve this.
To find the number of sequences with at least one repeated letter, we subtract the number of sequences with no repeated letters from the total number of sequences.
The number of sequences with no repeated letters can be found by choosing 11 distinct letters from the alphabet, which is C(26, 11).
Therefore, the number of sequences with at least one repeated letter is 318,937,572,165 - C(26, 11).
To know more about sequences refer here:
https://brainly.com/question/30262438
#SPJ11
Ram bought a radio for Rs.1500 and sold it for Rs. 1200. What was his profit or loss percent? find it
Answers
300/1500x100= 20% loss
Find 3 ratios that are equivalent to the given ratio.
3/4
Answers
Answer:
12/16
That’s one
Converting Real Life Scale.. -Page 2-
NEED HELP ASAPPP 50 POINTS
(picture is linked belowww)
tysm like fr <33

Answers
The table with the scale measurements is given by the image shown at the end of the answer.
How to obtain the measurements?The measurements are obtained applying the proportion given for each table.
The symbols are given as follows:
': feet.'': inches.For the first table, we have that every inch on the table represents one feet in real life, hence:
2'' on the paper represents 2' in real life.2' on the paper represents 24' in real life. (as one feet = 12 inches, hence 24 inches = 24 feet according to the scale).0.5'' on the paper represents 0.5' in real life.9'' on the paper represents 9' in real life.For the second table, we have that every inch on the paper represents two feet in real life, hence the measurements are given as follows:
2'' on the paper represents 4' in real life.2' on the paper represents 48' in real life.0.5'' on the paper represents 1' in real life.9'' on the paper represents 18' in real life.More can be learned about scale measurements at https://brainly.com/question/29229124
#SPJ1

Two sides and an angle (SSA) of a triangle are given. Determine whether the given
produce one triangle, two triangles, or no triangle at all. Solve each triangle that
measurements
results.
a = 17,
c = 18.3
A = 56°
Answers
Answer:
no triangle at all
Step-by-step explanation:
When two sides and an angle (SSA) of a triangle are given, we can use the Law of Cosines to determine whether the given measurements produce one triangle, two triangles, or no triangle at all.
The Law of Cosines states that in any triangle ABC, c² = a² + b² - 2ab cos(C), where a, b, and c are the lengths of the sides of the triangle and A, B, and C are the measures of the angles opposite those sides.
Given a = 17, c = 18.3, and A = 56°, we can use the Law of Cosines to find the value of b²:
b² = c² - a² + 2ab cos(A)
If the value of b² is positive, then the given measurements produce one triangle. If the value of b² is zero, then the given measurements produce one degenerate triangle. If the value of b² is negative, then the given measurements do not produce any triangle.
Calculating b² = 18.3² - 17² + 2(17)(18.3)cos(56°) = 0.3
As the value of b² is zero, the given measurements produce one degenerate triangle. A degenerate triangle is a triangle whose sides do not form a valid triangle, i.e the three sides are collinear.
Since, the value of b² is zero, it means that the three sides of the triangle are collinear and it will not form a triangle. The measurements provided do not produce any triangle.
i need this done today whoever gets this correct gets brainliest!!! PLZZ HELPP MEE

Answers
Answer:
$2.75
Step-by-step explanation:
Answer:
$68.75 $2.75
Step-by-step explanation:
sixty eight dollars and seventy five cents <-- multiplied
two dollars and seventy five cents <-- per
(1) Find the volume in the first octant bounded by y^2=4−x and y=2z
(2) Find the volume bounded by z=x^2+y^2and z=4
Answers
the volume in the first octant bounded by\(y^2=4−x\) and y=2z is pi/36 sqrt(3).
(1) To find the volume in the first octant bounded by the surfaces \(y^2 = 4 - x\) and y = 2z, we can set up a triple integral in cylindrical coordinates.
First, we need to determine the bounds for our variables. Since we are working in the first octant, we know that 0 <= z, 0 <= theta <= pi/2, and 0 <= r.
Next, we need to find the equation for the upper and lower bounds of z in terms of r and theta. We can start with the equation \(y^2 = 4 - x\) and substitute y = 2z to get:
\((2z)^2 = 4 - x\)
\(4z^2 = 4 - x\)
\(x = 4 - 4z^2\)
We can then use this equation along with the equation z = y/2 to get the bounds for z:
\(0 < = z < = (4 - x)^(1/2)/2 = (4 - 4z^2)^(1/2)/2\)
Squaring both sides, we get:
\(0 < = z^2 < = (1 - z^2)/2\)
\(0 < = 2z^2 < = 1 - z^2\)
\(z^2 < = 1/3\)
So the bounds for z are:
\(0 < = z < = (1/3)^(1/2)\)
Finally, we can set up the triple integral in cylindrical coordinates:
V = ∫∫∫ r dz dtheta dr
with bounds:
0 <= r
0 <= theta <= pi/2
\(0 < = z < = (1/3)^(1/2)\)
and integrand:
r
So the volume in the first octant bounded by y^2=4−x and y=2z is:
V = ∫∫∫ r dz dtheta dr
= ∫ from 0 to\((1/3)^(1/2) ∫ from 0 to pi/2 ∫ from 0 to r r dz dtheta dr\)
= ∫ from 0 to\((1/3)^(1/2) ∫ from 0 to pi/2 r^2/2 dtheta dr\)
= ∫ from 0 to\((1/3)^(1/2) r^2 pi/4 dr\)
\(= pi/12 (1/3)^(3/2)\)
= pi/36 sqrt(3)
Therefore, the volume in the first octant bounded by\(y^2=4−x\) and y=2z is pi/36 sqrt(3).
(2) To find the volume bounded by z = x^2 + y^2 and z = 4, we can use a triple integral in cylindrical coordinates.
First, we need to determine the bounds for our variables. Since we are working in the region where z is bounded by \(z = x^2 + y^2\) and z = 4, we know that 0 <= z <= 4.
Next, we can rewrite the equation \(z = x^2 + y^2\) in cylindrical coordinates as \(z = r^2.\)
So the bounds for r and theta are:
0 <= r <= 2
0 <= theta <= 2pi
And the bounds for z are:
\(r^2 < = z < = 4\)
Finally, we can set up the triple integral in cylindrical coordinates:
V = ∫∫∫ r dz dtheta dr
with bounds:
0 <= r <= 2
0 <= theta <= 2pi
\(r^2 < = z < = 4\)
and integrand: 1
To know more about cylindrical coordinates, refer here:
https://brainly.com/question/30394340
#SPJ11
A box contains 22 pennies, 44 nickels, and 66 dimes. Six coins are drawn without replacement, with each coin having an equal probability of being chosen. What is the probability that the value of the coins drawn is at least 5050 cents
Answers
Answer:
127/924 ≈ 0.1374
Step-by-step explanation:
Given a box with 2 pennies, 4 nickels, 6 dimes, you want the probability that 6 randomly chosen coins will have a value of 50 cents or more.
50 centsThe ways 50 cents (or more) can be made from those coins are ...
6 dimes5 dimes + 1 nickel5 dimes + 1 penny4 dimes + 2 nickelsCount the waysThere is 6C6 = 1 way to choose 6 dimes.
There are (6C5)(4C1) = 6·4 = 24 ways to choose 5 dimes and 1 nickel
There are (6C5)(2C1) = 6·2 = 12 ways to choose 5 dimes and 1 penny
There are (6C4)(4C2) = 15·6 = 90 ways to choose 4 dimes and 2 nickels
The total number of ways to get 50¢ or more is ...
1 +24 +12 +90 = 127
The total number of ways to choose 6 coins from the 12 is ...
12C6 = 924
ProbabilityThe probability of choosing 6 coins that total 50¢ or more is ...
127/924 ≈ 0.1374
<95141404393>

what is the solution of -2x - 5y = -47 4x - 2y = -2
Answers
Answer:
x= 7/2 <--fraction y=8
Step-by-step explanation:
lmk if that is incorrect
Which value for the constant ccc makes w=5w=5w, equals, 5 an extraneous solution in the following equation? \sqrt{29+4w}=23-cw 29+4w =23−cw
Answers
Answer:
c=6
Step-by-step explanation:
In order to solve the original equation, we would have to square both sides of the equation:
\begin{aligned}\sqrt{29+4w}&=23-cw\\\\ \left(\sqrt{29+4w}\right)^2&=(23-cw)^2\\\\ 29+4w&=(23-cw)^2\end{aligned}
29+4w
(
29+4w
)
2
29+4w
=23−cw
=(23−cw)
2
=(23−cw)
2
However, squaring both sides of an equation can create extraneous solutions! [Why?]
Hint #22 / 4
Let's plug \blueD w=\blueD{5}w=5start color #11accd, w, end color #11accd, equals, start color #11accd, 5, end color #11accd into the last equation we obtained:
\begin{aligned}29+4\blueD w&=(23-c\blueD{w})^2\\\\ 29+4(\blueD 5)&=(23-c(\blueD{5}))^2\\\\ 49&=(23-5c)^2\end{aligned}
29+4w
29+4(5)
49
=(23−cw)
2
=(23−c(5))
2
=(23−5c)
2
This equation is correct, both when 23-5c=723−5c=723, minus, 5, c, equals, 7 and when 23-5c=-723−5c=−723, minus, 5, c, equals, minus, 7.
However, the original equation is not correct for 23-5c=-723−5c=−723, minus, 5, c, equals, minus, 7, since this way we obtain \sqrt{49}=-7
49
=−7square root of, 49, end square root, equals, minus, 7.
Hint #33 / 4
Therefore, an extraneous solution is obtained for the ccc-value that makes 23-5c23−5c23, minus, 5, c equal -7−7minus, 7, which is c=6c=6c, equals, 6.
Substituting this back into the original equation gives \sqrt{29+4w}=23-6w
29+4w
=23−6wsquare root of, 29, plus, 4, w, end square root, equals, 23, minus, 6, w. You can now solve this for www and see for yourselves that w=5w=5w, equals, 5 is indeed extraneous.
Hint #44 / 4
The answer is:
c=6c=6
c = 6, makes w = 5 an extraneous solution of the equation √(29 + 4w) = 23 - cw.
What are extraneous solutions?A root of a transformed equation that is not a root of the original equation because it was omitted from the domain of the original equation is referred to as an extraneous solution.
How to solve the question?In the question, we are asked to find the value for the constant c, that makes w = 5, an extraneous solution in the equation:
√(29 + 4w) = 23 - cw.
We first try to solve this equation, by squaring both sides,
29 + 4w = (23 - cw)²,
or, 29 + 4w = 23² - 2(23)(cw) + (cw)²,
or, 29 + 4w = 529 - 46cw + c²w²,
Now, we substitute w = 5, in the above equation to get:
29 + 4(5) = 529 - 46c(5) + c²(5)²,
or, 29 + 20 = 529 - 230c + 25c²,
or, 25c² - 230c + 480 = 0.
Solving this by the quadratic formula, we get:
\(c = \frac{-(-230)\pm \sqrt{(-230)^{2}-4(25)(480)}}{2(25)}\) ,
or, \(c = \frac{230\pm \sqrt{52900-48000}}{50}\) ,
or, \(c = \frac{230\pm \sqrt{4900}}{50}\) ,
or, \(c = \frac{230\pm 70}{50}\) ,
or, c = 300/50 or 160/50,
or, c = 6 or c = 3.2.
Now, we will check these values in the original equation by keeping w = 5.
When c = 6:
√(29 + 4w) = 23 - cw,
or, √(29 + 4(5)) = 23 - (6)(5),
or, √(29 + 20) = 23 - 30,
or, √49 = -7,
or, 7 = -7, which is not true.
Hence, c = 6 makes w = 5 an extraneous solution.
When c = 3.2,
√(29 + 4w) = 23 - cw,
or, √(29 + 4(5)) = 23 - (3.2)(5),
or, √(29 + 20) = 23 - 16,
or, √49 = 7,
or, 7 = 7, which is true.
Hence, c = 3.2 makes w = 5 a proper solution.
Therefore, c = 6, makes w = 5 an extraneous solution of the equation √(29 + 4w) = 23 - cw.
The question mentioned is not understandable. For proper question, refer to the attachment.
Learn more about extraneous solutions at
https://brainly.com/question/2959656
#SPJ2

Taub went shopping for a new pair of pants. Sales tax where she lives is 9%. The price of the pair of pants is $36. Find the total price including tax. Round to the nearest cent.
Answers
Answer:
$39.24 + tax
Step-by-step explanation:
what is 42-[28 divded by 7]+111
Answers
Answer: 149
Step-by-step explanation:
You start by solving using PEMDAS. Then you solve from left to right.
42-(28/7)+111
= 42-4+111
= 38+111
= 149
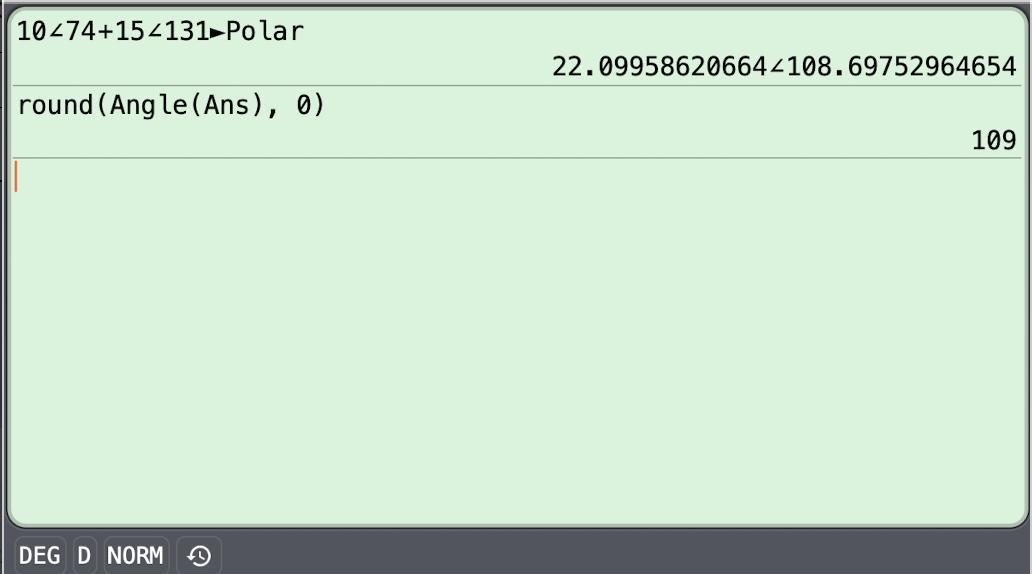
A ship sails on a bearing of 074° for 10 miles followed by a
bearing of 131° for 15 miles. Work out the bearing of the
ship from its starting position to the nearest degree.
Answers
Answer:
109°
Step-by-step explanation:
You want to know the bearing of a ship from its starting location after it sails 10 miles on a bearing of 74°, then 15 miles on a bearing of 131°.
Final bearingWe can add the travel vectors and express the result in polar form. The angle of that is the bearing angle from the starting position. The calculator result is shown in the second attachment.
The ship is at a bearing of 109° from its starting position.
Vector sumThe first attachment shows a diagram of the vector sum. The triangle internal angle opposite the resultant vector is shown. The two triangle side lengths (10 mi, 15 mi) can be used with the law of cosines to find the distance (OB) the ship is from its starting location.
Knowing that distance, we can use the law of sines to find angle AOB. Adding that angle to the initial bearing gives the bearing to the final location. The calculations for this are shown in the third attachment.
The ship is at a bearing of 109° from its starting position.
__
Additional comment
Of course, the geometry app used to draw the diagram in the first attachment can also measure the bearing to the final location.
The upshot is there are several ways to find the bearing of the final position.
The rectangular coordinates we use with the calculator for vector calculations are (north, east) coordinates. This avoids having to switch to angles measured counterclockwise from +x, and then back again to angles measured clockwise from +y.
<95141404393>


probability of rolling a factor of 45
Answers
Answer:
Step-by-step explanation:
POOP THEN PEEEEEE
Point a is located at (0, 4), and point b is located at (−2, −3). find the x value for the point that is 1 over 4 the distance from point a to point b.
Answers
The distance between the given points A and B is √65 units.
where, Point A is at (0 , 4) and Point B at (-2 , -3).
Given, a point A (0 , 4) and a point B (-2 , -3)
we have to find the distance between the given two points,
As, we know that to find the distance between two points in cartesian plane we have to use the distance formula i.e.
d = √((x1 - x2)² + (y1 - y2)²)
On using distance formula, we get
distance = √((x1 - x2)² + (y1 - y2)²)
distance = √(0 + 4)² + (4 + 3)²
distance = √16 + 49
distance = √65
So, if the points are located at A (0 , 4) and B (-2 , -3) then, the distance between the given points A and B is √65 units.
Hence, the distance between the given points A and B is √65 units as, point A is located at (0 , 4) and point B is located at (-2 , -3).
Learn more about Coordinate Geometry here https://brainly.com/question/18269861
#SPJ4
A plane intersects only one nappe of a double-napped cone such that it is parallel to a generating line. Which conic section is formed?.
Answers
When a plane intersects only one nappe of a double-napped cone such that it is parallel to a generating line, it forms a parabola.
When a plane intersects only one nappe of a double-napped cone parallel to a generating line, it forms a conic section known as a parabola. This is because a parabola is defined as the set of all points that are equidistant to a fixed point (known as the focus) and a fixed line (known as the directrix).
When a plane intersects a double-napped cone parallel to a generating line, it intersects all the generatrices at the same angle, resulting in a curve that is symmetric and opens in one direction. This curve is a parabola, and it is commonly found in nature, such as the path of a thrown ball, the shape of a satellite dish, or the reflector of a car's headlights.
The properties of a parabola make it useful in various fields, including optics, physics, and engineering, where it is used to model and analyze a wide range of phenomena, such as the trajectory of projectiles, the behavior of lenses and mirrors, and the design of antennas and reflectors.
To know more about parabola:
https://brainly.com/question/21685473
#SPJ4
There are five times as many pink buttons as yellow buttons.
number of yellow buttons : number of blue buttons = 4 : 7
e button is selected at random.
ork out the probability that the button is either pink or blue.
ve your answer as a fraction in its simplest form.
Optional working
nswer:
Write your fraction in the form a/b
Answers
Answer:
please put the number of yellow buttons if you can
thank you.
sketch the graph of the function. f(x, y) = sin(x)
Answers
To sketch the graph of the function f(x, y) = sin(x), we can visualize it as a surface in a three-dimensional coordinate system. The graph of the function f(x, y) = sin(x) represents a surface in three-dimensional space. The graph depicts a series of sinusoidal waves as x varies.
To sketch the graph of the function f(x, y) = sin(x), we can visualize it as a surface in a three-dimensional coordinate system. In this case, the function depends only on the variable x, while y remains constant. As x changes, the value of sin(x) varies, resulting in a series of wave-like patterns along the x-axis.
When sketching the graph, we can plot various points on the surface by selecting different values for x and y, and evaluating sin(x) at those points. As x increases or decreases, the graph will display the familiar oscillating pattern of the sine function. The amplitude and frequency of the waves will depend on the range and step size chosen for x.
It is important to note that the graph of f(x, y) = sin(x) is a surface and not a curve in the traditional sense. It represents a continuous variation of the sine function along the x-axis, with the y-coordinate remaining constant.
Learn more about sine function here:
Which
equation represents a line that passes through (-2, 4) and has a slope of 2/5?
Answers
Answer:y - 4 = 2/5(x + 2)
Step-by-step explanation:
Mark me brainliest
Oil spilled from a ruptured tanker spreads in a circle whose area increases at a constant rate of 8.5 mi^2/hr. How rapidly is radius of the spill increasing when the area is 7 mi^2?
Answers
To find the rate at which the radius of the oil spill is increasing when the area is 7 mi^2, dr/dt ≈ 0.203 mi/hr the area of the spill is 7 mi^2, dr/dt ≈ 0.203 mi/hr the radius is increasing at a rate of 0.203 mi/hr.
Where A is area and r is the radius. Taking the derivative of both sides with respect to time, we can express the rate of change of the area as dA/dt = 2πr(dr/dt). Given that dA/dt is constant at 8.5 mi^2/hr, we can substitute the values to find the rate at which the radius is increasing.
We have the equation dA/dt = 2πr(dr/dt), where dA/dt represents the rate of change of the area, r is the radius, and dr/dt is the rate at which the radius is changing. We are given that dA/dt is constant at 8.5 mi^2/hr. When the area is 7 mi^2, we can substitute these values into the equation: 8.5 = 2π(7)(dr/dt)
Simplifying the equation, we can solve for dr/dt: dr/dt = 8.5 / (2π(7)) Evaluating the expression, we find: dr/dt ≈ 0.203 mi/hr
Therefore, when the area of the spill is 7 mi^2, the radius is increasing at a rate of approximately 0.203 mi/hr.
To learn more about radius click here : brainly.com/question/13449316
#SPJ11