The following differential equation describes the movement of a body with a mass of 1 kg in a mass-spring system, where y(t) is the vertical position of the body in meters) at time t. y" + 4y + 5y = -21 To determine the position of the body at time t complete the following steps. (a) Write down and solve the characteristic (auxiliary) equation. (b) Determine the complementary solution, yc, to the corresponding homogeneous equation, y" + 4y' + 5y = 0. (c) Find a particular solution, Yp, to the nonhomogeneous differential equation, Y" + 4y' + 5y = e-21. Hence state the general solution to the nonhomogeneous equation as y = Ye + yp. (d) Solve the initial value problem if the initial position of the body is 1 m and its initial velocity is zero.
Answers
After considering the given data we conclude that
a) r = -2 + i and r = -2 - i value generated after solving the auxiliary equation
b)\(y_c = c_1e^{(-2t)} cos(t) + c_2e^{(-2t)} sin(t)\) complementary solution
c) general solution to the nonhomogeneous equation is \(y = y_c + Y_p = c_1e^{(-2t)} cos(t) + c_2e^{(-2t)} sin(t) + (1/26)e^{(-21)} .\)
d) initial value problem is \(y(t) = e^{(-2t)} (cos(t) + 2sin(t))/2 + (1/26)e^{(-21)} .\)
To determine the position of the body at time t, we can apply the given differential equation to solve for y(t). To do this, we can follow the steps below:
(a) the characteristic (auxiliary) equation is
The characteristic equation is obtained by setting the coefficients of the differential equation to zero, which gives us the equation \(r^2 + 4r + 5 = 0.\)Solving this quadratic equation, we get r = -2 + i and r = -2 - i.
(b) evaluate the complementary solution, yc, to the corresponding homogeneous equation, \(y" + 4y' + 5y = 0.\)
The complementary solution is given by\(y_c = c_1e^{(-2t)} cos(t) + c_2e^{(-2t)} sin(t),\)where \(c_1\) and \(c_2\) are constants determined by the initial conditions.
(c) Calculate a particular solution, Yp, to the nonhomogeneous differential equation, \(Y" + 4y' + 5y = e^{(-21)}\). Hence state the general solution to the nonhomogeneous equation as \(y = y_c + y_p.\)
To describe a particular solution, we can use the method of undetermined coefficients and guess a solution of the form \(Yp = Ae^{(-21)}\), where A is a constant to be determined.
Staging this into the differential equation, we get A = 1/26. Therefore, the particular solution is \(Y_p = (1/26)e^{(-21)}\). The general solution to the nonhomogeneous equation is \(y = y_c + Y_p = c_1e^{(-2t)} cos(t) + c_2e^{(-2t)} sin(t) + (1/26)e^{(-21)}\)
(d) Solve the initial value problem if the initial position of the body is 1 m and its initial velocity is zero.
Applying the initial conditions, we can solve for the constants \(c_1\) and \(c_2\) in the complementary solution. Since the initial velocity is zero, we have \(y'(0) = -2c_1 + c_2 = 0\), which gives us \(c_2 = 2c_1.\)
Applying the initial position, we have \(y(0) = c_1 = 1\), which gives us \(c_2 = 2.\)Therefore, the solution to the initial value problem is \(y(t) = e^{(-2t)} (cos(t) + 2sin(t))/2 + (1/26)e^{(-21)}\)
To learn more about differential equation
https://brainly.com/question/28099315
#SPJ4
Related Questions
Find the degree of the monomial.
s8t
The degree is

Answers
Answer:
Step-by-step explanation:
the degree of 8^8t
16777216t : the degree of the mnonmial is 1, because the degree of the variable is 1
What is m less than 8 thirds greater than or equal to negative 19
Answers
Answer:
greater then tell me if i'm wrong
The probability of being dealt a royal straight flush (ace, king, queen, jack, and ten of the same suit) in poker is about 1.3 × 10–8. Suppose that an avid poker player sees 100 hands a week, 52 weeks a year, for 20 years.
a. What is the probability that she is never dealt a royal straight flush dealt?
b. What is the probability that she is dealt exactly two royal straight flushes?
Answers
a. The probability that she is never dealt a royal straight flush in 100 hands is approximately 0.999999087.
b. The probability that she is dealt exactly two royal straight flushes in 100 hands is approximately 4.455 × 10^(-11).
To solve this problem, we can use the concept of the binomial probability distribution.
a. Probability of never being dealt a royal straight flush in one hand:
The probability of not being dealt a royal straight flush in one hand is 1 minus the probability of being dealt a royal straight flush. So the probability of not being dealt a royal straight flush in one hand is approximately 1 - 1.3 × 10^(-8) ≈ 1.
Since the events of being dealt a royal straight flush in different hands are independent, we can multiply the probabilities of not being dealt a royal straight flush in each hand to find the probability of not being dealt a royal straight flush in all 100 hands.
Probability of not being dealt a royal straight flush in all 100 hands:
P(not dealt royal straight flush in one hand)^100 = 1^100 = 1.
Therefore, the probability that she is never dealt a royal straight flush in 100 hands is 1.
b. Probability of being dealt exactly two royal straight flushes:
To calculate the probability of being dealt exactly two royal straight flushes, we can use the binomial probability formula.
Probability of getting exactly k successes in n trials is given by:
P(X = k) = C(n, k) * p^k * (1 - p)^(n - k),
where C(n, k) is the binomial coefficient (n choose k), p is the probability of success in one trial, and n is the number of trials.
In this case, n = 100 (number of hands), k = 2 (exactly two royal straight flushes), and p = 1.3 × 10^(-8) (probability of being dealt a royal straight flush in one hand).
Using the formula, we can calculate the probability of being dealt exactly two royal straight flushes:
P(X = 2) = C(100, 2) * (1.3 × 10^(-8))^2 * (1 - 1.3 × 10^(-8))^(100 - 2).
The binomial coefficient C(100, 2) can be calculated as C(100, 2) = 100! / (2! * (100 - 2)!) = 4,950.
Substituting the values into the formula:
P(X = 2) = 4,950 * (1.3 × 10^(-8))^2 * (1 - 1.3 × 10^(-8))^(98)
Calculating the expression gives us:
P(X = 2) ≈ 4.455 × 10^(-11)
So, the probability that she is dealt exactly two royal straight flushes in 100 hands is approximately 4.455 × 10^(-11).
To learn more about probability visit : https://brainly.com/question/13604758
#SPJ11
One taxi company charges $12.50 plus $0.15 per mile for a fare to the airport. Another taxi
company charges $6.50 plus $0.35 per mile for the same fare. For how many miles will the two
companies charge the same amount?
HELP ME PLEASE ‼️‼️‼️
Answers
Answer:
Step-by-step e I can use inequalities to solve word problems with one or more ... Money: The coupon is good for any item that costs less than $10. ... than or equal to ban ... Yellow Cab Taxi charges a $1.75 flat rate in addition to $0.65 per mile. ... has a cell phone plan that charges $0.07 per minute plus a monthly fee of $19.00.xplanation:
A bicycle manufacturer is studying the reliability of one of its models. The study finds that the probability of a brake defect is 4 percent and the probability of both a brake defect and a chain defect is 1 percent. If the probability of a defect with the brakes or the chain is 6 percent, what is the probability of a chain defect? 1. 5 percent 2 percent 2. 5 percent 3 percent.
Answers
The bicycle manufacturer is studying the reliability of its models and analyzing the probability of defects. They found the probability of a brake defect is 4 percent and the probability of both brake and chain defects is 1 percent.
Given that the probability of a defect with brakes or chain is 6 percent, we can find the probability of a chain defect using the formula: P(A and B) = P(A|B) * P(B), where P(A and B) is the probability of both events A and B occurring, P(A|B) is the probability of event A occurring given that event B has occurred, and P(B) is the probability of event B occurring.
In this case, we want to find the probability of a chain defect given that there is a defect with either the brakes or the chain. Let's use the events: A = brake defect, B = chain defect, From the problem statement, we know that: P(A) = 0.04 (probability of a brake defect), P(A and B) = 0.01 (probability of both a brake defect and a chain defect)
P(A or B) = 0.06 (probability of a defect with the brakes or the chain).
To find P(B|A or B), we can use the formula: P(B|A or B) = P(A and B) / P(A or B) = 0.01 / 0.06, = 1/6, = 0.1667, So the probability of a chain defect given that there is a defect with either the brakes or the chain is 16.67%, or approximately 2/12 or 1/6.
Therefore, the correct answer is option 2: 2%, Solving for the probability of a chain defect, we get: P(chain defect) = 0.06 - 0.04 + 0.01 = 0.03, So, the probability of a chain defect is 3 percent.
To know more about probability click here
brainly.com/question/15124899
#SPJ11
Cynthia rounds a number x to one decimal place the result is 6.3 write down the error interval for x
Answers
Answer:
6.25 ≤ x ≤6.34
Step-by-step explanation:
Given that:
Number, x rounded to 1 decimal place = 6.3
The lowest value number x could be is ;
6.25, rounding 6.25 to 1 decimal place = 6.3
The highest value number x could be is ;
6.34, rounding 6.34 to 1 decimal place = 6.3
Hence, the error interval for X is
Lowest possible value ≤ x ≤ highest possible value
6.25 ≤ x ≤6.34
Find the radius of a circle that has a circumference of 16
Answers
Answer:
r≈2.55
hope this helps!
Michelle bought 12 cookies and 8 cupcakes for $72. Jana bought 5 of the same cookies and 10 of the same cupcakes for $50. What is the price of each item?
Answers
5x+10y=50
X=cookies, y=cupcakes
Cookies are 4$ each and cupcakes are 3$ each
Answer:
Step-by-step explanation:
x = cookies
y= cupcakes
12x + 8y = 72
5x + 10y = 50
60x + 40y = 360
-20x - 40y = -200
40x = 160
x = $4 each cookie
12(4) + 8y = 72
48 + 8y = 72
8y = 24
y = $3 each cupcake
5. Find the Fourier coefficients of the periodic ( -5 to 5) function y(t) = -3 when -5
Answers
In summary, the Fourier coefficients for the periodic function y(t) = -3 on the interval -5 ≤ t ≤ 5 are:
c₀ = -3 (DC component)
cₙ = 0 for n ≠ 0 (other coefficients)
To find the Fourier coefficients of the periodic function y(t) = -3 on the interval -5 ≤ t ≤ 5, we can use the formula for Fourier series coefficients:
cn = (1/T) ∫[t₀-T/2, t₀+T/2] y(t) \(e^{(-i2\pi nt/T)}\) dt
where T is the period of the function and n is an integer.
In this case, the function y(t) is constant, y(t) = -3, and the period is T = 10 (since the interval -5 ≤ t ≤ 5 spans 10 units).
To find the Fourier coefficient c₀ (corresponding to the DC component or the average value of the function), we use the formula:
c₀ = (1/T) ∫[-T/2, T/2] y(t) dt
Substituting the given values:
c₀ = (1/10) ∫[-5, 5] (-3) dt
= (-3/10) \([t]_{-5}^{5}\)
= (-3/10) [5 - (-5)]
= (-3/10) [10]
= -3
Therefore, the DC component (c₀) of the Fourier series of y(t) is -3.
For the other coefficients (cₙ where n ≠ 0), we can calculate them using the formula:
cₙ = (1/T) ∫[-T/2, T/2] y(t)\(e^{(-i2\pi nt/T) }\)dt
Since y(t) is constant, the integral becomes:
cₙ = (1/T) ∫[-T/2, T/2] (-3) \(e^{(-i2\pi nt/T)}\) dt
= (-3/T) ∫[-T/2, T/2] \(e^{(-i2\pi nt/T)}\) dt
The integral of e^(-i2πnt/T) over the interval [-T/2, T/2] evaluates to 0 when n ≠ 0. This is because the exponential function oscillates and integrates to zero over a symmetric interval.
all the coefficients cₙ for n ≠ 0 are zero.
To know more about function visit:
brainly.com/question/30721594
#SPJ11
Find the matrix A that has the given eigenvalues and corresponding eigenvectors. ^1 ---- () ---- () ---- () {}} = -1 = 0 = 1
Answers
The eigenvectors are given as:
v1 = {1,0,−1}v2 = {1,−1,0}v3 = {1,1,1}
For calculating the matrix A, the first step is to form a matrix that has the eigenvectors as the columns.
That is, A = [v1 v2 v3]
Now, let's find the eigenvectors.
For eigenvalue 1, the eigenvector v3 is obtained by solving
(A − I)v = 0 where I is the identity matrix of size 3.
That is, (A − I)v = 0A − I = [[0,-1,-1],[0,-1,-1],[0,-1,-1]]
Therefore, v3 = {1,1,1} is the eigenvector corresponding to the eigenvalue 1.
Similarly, for eigenvalue −1, the eigenvector v1 is obtained by solving (A + I)v = 0,
and for eigenvalue 0, the eigenvector v2 is obtained by solving Av = 0.
Solving (A + I)v = 0, we get,
(A + I) = [[2,-1,-1],[-1,2,-1],[-1,-1,2]]
Therefore, v1 = {1,0,−1} is the eigenvector corresponding to the eigenvalue −1.
Solving Av = 0, we get,
A = [[0,1,1],[-1,0,1],[-1,1,0]]
Therefore, the matrix A that has the given eigenvalues and corresponding eigenvectors is:
A = [[0,1,1],[-1,0,1],[-1,1,0]]
In linear algebra, eigenvalues and eigenvectors have applications in several areas, including physics, engineering, economics, and computer science. The concept of eigenvectors and eigenvalues is useful for understanding the behavior of linear transformations. In particular, an eigenvector is a nonzero vector v that satisfies the equation Av = λv, where λ is a scalar known as the eigenvalue corresponding to v. The matrix A can be represented in terms of its eigenvalues and eigenvectors, which is useful in many applications. For example, the eigenvalues of A give information about the scaling of A in different directions, while the eigenvectors of A give information about the direction of the scaling. By finding the eigenvectors and eigenvalues of a matrix, it is possible to diagonalize the matrix, which can simplify calculations involving A. In summary, the concept of eigenvectors and eigenvalues is an important tool in linear algebra, and it has numerous applications in science, engineering, and other fields.
Therefore, the matrix A that has the given eigenvalues and corresponding eigenvectors is A = [[0,1,1],[-1,0,1],[-1,1,0]]. The concept of eigenvectors and eigenvalues is an important tool in linear algebra, and it has numerous applications in science, engineering, and other fields. The eigenvectors of A give information about the direction of the scaling.
To know more about linear algebra visit:
brainly.com/question/26460398
#SPJ11
I need help graphing this function its a multiple choice question please help i will show all choices

Answers
Notice that the given function is an exponential function, also:
\(y=30(\frac{1}{4})^x,\)therefore, its y-intercept is y=30.
Answer:
6. what are the two most generic and widely used valuation multiples?
Answers
The two most generic and widely used valuation multiples in finance and investment analysis are the price-to-earnings (P/E) ratio and the enterprise value-to-earnings before interest, taxes, depreciation, and amortization (EV/EBITDA) multiple.
1. Price-to-Earnings (P/E) Ratio: The P/E ratio is calculated by dividing the market price per share of a company's stock by its earnings per share (EPS). It provides a measure of how much investors are willing to pay for each dollar of earnings generated by the company.
A high P/E ratio suggests that investors have high expectations for future growth and are willing to pay a premium for the stock. On the other hand, a low P/E ratio may indicate that the stock is undervalued or that investors have low expectations for future growth.
2. Enterprise Value-to-EBITDA (EV/EBITDA) Multiple: The EV/EBITDA multiple is calculated by dividing the enterprise value (EV) of a company by its earnings before interest, taxes, depreciation, and amortization (EBITDA).
The EV is the total market value of a company's equity and debt, minus its cash and cash equivalents. EBITDA represents the company's operating earnings before accounting for interest, taxes, depreciation, and amortization.
The EV/EBITDA multiple is commonly used in evaluating the valuation of companies, especially in the context of mergers and acquisitions. It provides a measure of a company's overall value relative to its earnings, without being affected by capital structure or tax considerations.
Both the P/E ratio and EV/EBITDA multiple are widely used because they are relatively easy to calculate and understand. However, it's important to note that these multiples have limitations and should be used in conjunction with other valuation methods and qualitative analysis to make informed investment decisions.
To know more about valuation methods refer here:
https://brainly.com/question/30478023#
#SPJ11
The morris family drove 368. 5 miles in 5. 5 hours. Determine their rate of speed
Answers
The distance driven by morris family is \(368.5\) miles in \(5.5\) hours. Using this, their rate of speed is found to be \(67\) miles per hour.
Rate of speed is defined as the total movement of a body in a definite time interval. To determine the rate of speed at which the Morris family drove, we need to divide the distance they covered by the time it took them to cover it. Therefore, the rate of speed can be calculated using the formula as follows:
Rate of speed\(=\frac{Distance}{Time}\)
Given that the Morris family drove \(368.5\) miles in \(5.5\) hours, we can substitute these values in the formula above:
Rate of speed\(=\frac{368.5}{5.5}\)
Simplifying the above expression, we get:
Rate of speed\(=67\) miles per hour
Therefore, the Morris family's rate of speed was \(67\) miles per hour.
Learn more about rate of speed here:
https://brainly.com/question/18404426
#SPJ11
let f(x,y). find the directions u and the values of f(1,1) for which the following is true. a. f(1,1) is largest b. f(1,1) is smallest c. f(1,1)0 d. f(1,1)4 e. f(1,1)3
Answers
The directions of the function where it equals 3 are given by the vectors u for which ∇f(1,1) · u = 0.
What is Function ?
function can be defined in which it relates an input to output.
To find the directions u and the values of f(1,1) for which the following is true, we need to use the gradient of the function f(x, y). The gradient is a vector that points in the direction of the maximum increase of the function.
The gradient of f(x, y) is given by:
∇f(x,y) = ( ∂f/∂x , ∂f/∂y )
a. To find the direction u for which f(1,1) is largest, we need to find the direction of the maximum increase of the function at the point (1,1). The direction of the maximum increase is given by the gradient vector ∇f(1,1). We need to find the unit vector u in the direction of ∇f(1,1).
So, first, we need to calculate the gradient at (1,1):
∇f(1,1) = ( ∂f/∂x , ∂f/∂y ) at (1,1)
b. To find the direction u for which f(1,1) is smallest, we need to find the direction of the maximum decrease of the function at the point (1,1). The direction of the maximum decrease is given by the negative of the gradient vector -∇f(1,1). We need to find the unit vector u in the direction of -∇f(1,1).
So, first, we need to calculate the gradient at (1,1):
-∇f(1,1) = - ( ∂f/∂x , ∂f/∂y ) at (1,1)
c. To find the directions u for which f(1,1) > 0, we need to find the directions of the function where it is positive at the point (1,1). The directions of the function where it is positive are given by the vectors u for which ∇f(1,1) · u > 0.
So, first, we need to calculate the gradient at (1,1):
∇f(1,1) = ( ∂f/∂x , ∂f/∂y ) at (1,1)
Then, we need to find the unit vectors u for which ∇f(1,1) · u > 0.
d. To find the directions u for which f(1,1) = 4, we need to find the directions of the function where it equals 4 at the point (1,1). The directions of the function where it equals 4 are given by the vectors u for which ∇f(1,1) · u = 0.
So, first, we need to calculate the gradient at (1,1):
∇f(1,1) = ( ∂f/∂x , ∂f/∂y ) at (1,1)
Then, we need to find the unit vectors u for which ∇f(1,1) · u = 0.
e. To find the directions u for which f(1,1) = 3, we need to find the directions of the function where it equals 3 at the point (1,1).
Therefore, The directions of the function where it equals 3 are given by the vectors u for which ∇f(1,1) · u = 0
To learn more about Function from given link.
https://brainly.com/question/12431044
#SPJ1
One house sitter charges $40 a day. Another house sitter charges an initial fee of $100 plus $15 per day. Which equation could you use to solve to find out after how many days is the fee charged by the two sitters the same?
Answers
The two sitters charge the same amount by 4 days.
Given data;
One home watch provider bills $40 per day. The initial pay for another house sitter is $100 plus $15 per day. Which equation could you use to solve to determine how many days later the two sitters' fees are equal?
To solve this case, assume;
'x' is the days required to get equal charges.
'y' is the final charge.
40 * x = y
100 + (15 * x) = y
From the above equations;
40 * x = 100 + (15 * x)
40 * x - 15 * x = 100
x = 4
Hence, 4 days is the fee charged by the two sitters are the same.
To learn more about equations click here:
brainly.com/question/14686792
#SPJ4
To be able to go on a trip to South America, Salma decides to save for 2 years. She opens a savings account with $700 . The account pays simple interest at an annual rate of 5% . She doesn't make any more deposits.
(a) How much total interest will Salma earn?
(b) What will the total amount in the account be (including interest)?
Answers
Answer:
(a) I'm pretty sure it's $71.75
(b) the total would be $771.75 if i calculated it right...
What value correctly fills in the blank so that the expressions are equivalent?
32 + 72 = blank x (4 + 9)
4
8
12
13
Answers
Answer: The answer is 8 because you add 32 + 72 and get 104 x and then 4 +9 = 13 then you divide 104 divided by 13 = 8
Answer:
8, because you add 32 and 72, which will get 104x and then 4+9 which is 13 then you divide 104 divided by 13 = 8
Step-by-step explanation:
hope this helps!
Cup o’ Coffee buys its coffee for $1.25 a cup. The coffee shop then sells each cup for $3.75. What is the percent markup for a cup of coffee?
Answers
Answer:
47%
Step-by-step explanation:
.375 × .125 = .046875
rounding up, 5 keeps the 7 as is, 7 is greater than 5, therefore the 8, becomes a 9, 9 is greater than 5, so the 6 becomes a 7, .047.
move the decimal three digits to the left and you get, 47%.
Hope this helps brainlest? please
graph each image as well as the figure after each dilation with the origin as it's center and the given scale factor.
X(-3, 1), Y(-1, 2), Z(2, 1) K = 2
Answers
Answer:
Step-by-step explanation:
To perform a dilation with a center at the origin and a scale factor of 2, we multiply each coordinate by 2.
For point X(-3, 1):
x-coordinate: -3 * 2 = -6
y-coordinate: 1 * 2 = 2
So the image of point X after the dilation is X'(-6, 2).
For point Y(-1, 2):
x-coordinate: -1 * 2 = -2
y-coordinate: 2 * 2 = 4
So the image of point Y after the dilation is Y'(-2, 4).
For point Z(2, 1):
x-coordinate: 2 * 2 = 4
y-coordinate: 1 * 2 = 2
So the image of point Z after the dilation is Z'(4, 2).
Graph of the original triangle XYZ:
Y(0, 2)
/\
/ \
/____\
X(0, 0) Z(3, 0)
Graph of the triangle after dilation
Y'(-2, 4)
/\
/ \
/____\
X'(-6, 0) Z'(4, 0)
its hard
What is the Volume and Surface Area of the following figure?
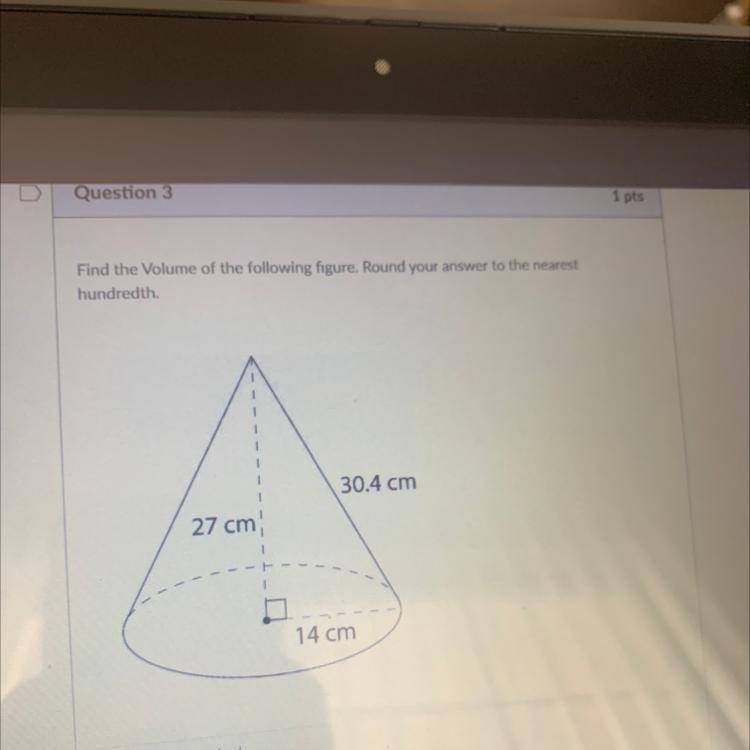
Answers
Answer:
71.4
Step-by-step explanation:
you wiil plus it by 30.4+27+14 that is how i got71.4
Whats 1+1 and 2+2 and 3+7 I’m in the first grade
Answers
Answer:
1 answer is 2
2 answer 4
3 answer 10
Step-by-step explanation:
Add 1+1
get 2
Add 2+2
get 4
Add 3+7
get 10
Question 1 (Multiple Choice Worth 1 points)
(02.04 LC)
A student is running a 10-kilometer race. He runs 1 kilometer every 4 minutes. Select the function that describes his distance from the finish line after x minutes.
1: f(x)=1/4x+10
2: f(x)=-1/10x+4
3: f(x)=1/10+4
4: f(x)=-1/4x+10
Answers
The correct function that describes the student's distance from the finish line after x minutes is f(x) = -1/4x + 10.
The correct function that describes the student's distance from the finish line after x minutes can be determined by analyzing the given information. We know that the student runs 1 kilometer every 4 minutes, and the race is a total of 10 kilometers.
Let's examine the options:
1. f(x) = 1/4x + 10
This function represents the distance covered by the student in x minutes, but it does not account for the fact that the total race distance is 10 kilometers.
2. f(x) = -1/10x + 4
This function has a negative coefficient for x, which would indicate that the student is getting farther away from the finish line as time progresses, which is not the case.
3. f(x) = 1/10 + 4
This function is a constant and does not change with time, so it cannot describe the student's distance from the finish line.
4. f(x) = -1/4x + 10
This function correctly represents the student's distance from the finish line. The negative coefficient for x indicates that the distance decreases as time progresses, and the constant term of 10 represents the initial distance from the finish line, which is 10 kilometers.
For more such questions on function
https://brainly.com/question/11624077
#SPJ8
_____ is the process of drawing conclusions about unknown characteristics of a population from which data were taken.
Answers
Answer:
Statistical inference
Step-by-step explanation:
Determine the
percent of the population for the following given that mu = 100 and
sigma = 15 Draw a picture and record the values, showing your
work
C. X ≥ 124.75
Answers
We can use the standard normal distribution table or calculate the z-score and find the corresponding area under the curve. The percentage of the population for X ≥ 124.75 is approximately 3.86%.
To find the percentage of the population for X ≥ 124.75, we need to calculate the z-score, which represents the number of standard deviations an observation is from the mean. The formula for the z-score is:
z = (X - μ) / σ
In this case, X is 124.75, μ is 100, and σ is 15. Plugging in these values, we get:
z = (124.75 - 100) / 15 = 1.65
Using the standard normal distribution table or a calculator, we can find the area under the curve to the right of the z-score of 1.65. The area represents the percentage of the population for X ≥ 124.75.
From the standard normal distribution table, we find that the area to the right of the z-score 1.65 is approximately 0.0495. Multiplying this by 100, we get 4.95%.
However, since we are interested in X ≥ 124.75, we need to consider the area to the left of the z-score of 1.65 and subtract it from 1. This gives us:
1 - 0.0495 = 0.9505
Multiplying 0.9505 by 100, we find that the percentage of the population for X ≥ 124.75 is approximately 95.05%. Therefore, the percentage of the population for X ≥ 124.75 is approximately 3.86%.
Learn more about population here:
https://brainly.com/question/31598322
#SPJ11
a roulette wheel has the numbers 1 through 36, 0, and 00. a bet on three numbers pays 11 to 1 (that is, if you bet $1 and one of the three numbers you bet comes up, you get back your $1 plus another $11). how much do you expect to win with a $1 bet on three numbers? hint [see example 4.] (round your answer to the nearest cent.)
Answers
With a $1 bet on three numbers, you can expect to win $12.33. So, the expected winnings for a $1 bet on three numbers in a roulette wheel is approximately $0.95.
Here's how to calculate it:
- There are 38 possible outcomes on the roulette wheel (1 through 36, 0, and 00).
- Your bet covers 3 of those outcomes, so your probability of winning is 3/38.
- The payout for a winning bet is $1 plus another $11, for a total of $12.
- To find your expected winnings, multiply the probability of winning by the payout:
(3/38) x $12 = $0.947
- Rounded to the nearest cent, that's $0.95.
So with a $1 bet on three numbers, you can expect to win about $0.95 each time, on average. Over many bets, your total winnings will approach $12.33.
In order to calculate the expected winnings from a $1 bet on three numbers in a roulette wheel, we can follow these steps:
1. Determine the probability of winning the bet. In a roulette wheel with 38 numbers (1-36, 0, and 00), you bet on three numbers, so the probability of winning is 3/38.
2. Determine the amount you would win if your bet is successful. Since the bet pays 11 to 1, you would get back your original $1 plus another $11, for a total of $12.
3. Multiply the probability of winning by the amount you would win. This will give you the expected winnings for a single $1 bet:
(3/38) * $12 = $0.947
So, the expected winnings for a $1 bet on three numbers in a roulette wheel is approximately $0.95 (rounded to the nearest cent).
Visit here to learn more about roulette wheel:
brainly.com/question/20114211
#SPJ11
A large pond takes up 2,700 square meters of land. If the length of the pool is 60 meters, what is the measurement of the width?
Answers
Given f(x) = –3x – 4, find f(–5).
Answers
Answer:
3x
Step-by-step explanation:
because if f is -5, -5=-3x-4, -5+4, -1=-3 divide and get 3=x
SOMEONE HELP ME PLEASE!!!

Answers
Answer:
32 seria tu respuesta amigo denada
in 2012, the general social survey included a question that asked participants how many hours they worked a week on household chores. do females spend more hours working on household chores than males? would this be an example of independent or dependent samples?
Answers
Using sampling concepts, it is found that this is an example of independent samples.
For dependent samples, there is a paired measurement for one set of items.For independent samples, separate measurements are made on two different sets, that is, the value on one sample reveal no information about the values on the other sample.In this problem, there are two sets of items, the data-set composed by the time taken by females, and the time taken by males.
Due to the multiple sets, it is an independent sample.A similar problem is given at https://brainly.com/question/25784076
Help would be much appreciated

Answers
Answer:
Figure is not accurate but i drew AE such that it is equal to BD and ED is equal to AB and AE is perpendicular to CD. And also ABDE is a rectangle.
Step-by-step explanation:
CD:AB
or, let CD be x
now
CD:AB= 1.5:1
or, x : 1.7 = 1.5 : 1
or, x/1.7 = 1.5/1
or, x = 2.6 m
CD = 2.6 m
ED=AB=1.7 m
now
CD = CE + ED
or, 2.6m =CE + 1.7m
or, CE = 2.6 m - 1.7 m
so, CE = 0.9 m
now
triangle CEA is a right angled triangle,
In triangle CEA, taking 52 as reference angle
tan52° = p/b
or,tan52° = CE/AE
or, tan52° = 0.9/AE
or, AE = 0.9/tan52°
so, AE = 0.7
now
AE = BD (given in the figure i uploaded)
so, BD = 0.7 m
