The diagonal of a TV screen is 42 inches. The base is 38
inches wide. How tall is the TV? Round your answer to the
nearest tenth.
42 inches
38 inches
When entering your answer, just give me the numerical
value, do NOT include "inches".
Round your answer to the nearest whole number,

Answers
Answer:
Diagonal measurement of a tv screen = 42 inches.
Base = 38 inches
To find:
The height of the tv.
Solution:
Let h be the length of the tv.
According to the Pythagoras theorem,
Taking square root on both sides.
Therefore, the height of the tv is inches.
Step-by-step explanation:
Answer:
92
Step-by-step explanation:
Divided by 72 equals 82.
So we then add by 42 and we have a result of 92.
Related Questions
Question Prog
A regular pentagon ABCDE is shown.
Work out the size of angle x.
D
A
C
B

Answers
The value of the angle x of the given pentagon is: x = 36°
How to find the angle in the polygon?The formula to find the interior angle of a regular polygon is:
θ = 180(n - 2)/n
where n is number of sides of polygon
In this case we have a pentagon which has 5 sides. Thus:
θ = 180(5 - 2)/5
θ = 540/5
θ = 108°
Now, the sides of the pentagon are equal and as such the triangle formed ΔBDC is an Isosceles triangle where:
∠BDC = ∠DBC
Thus:
x = (180 - 108)/2
x = 72/2
x = 36°
Read more about Polygon Angle at: https://brainly.com/question/1592456
#SPJ1
I need help with this pls

Answers
Answer:
a. is 3/8 b. is 4 5/12
Step-by-step explanation:
Answer:
3 / 8, 4[ 5 / 12]
Step-by-step explanation:
5 / 8 - 1 / 4
= 5 / 8 - 2 / 8
= 3 / 8
6 [1 / 6] - 1 [3 / 4]
= 6[2 / 12] - 1[9 / 12]
= 4[ 5 / 12]
Use elementary row operations to transform the augmented coefficient matrix to echelon form. Then solve the system by back substitution. X₁-4x2 +5x3. = 23 2x₁ + x₂ + x3 = 10 -3x + 2x₂-3x3 = = -23 *** An echelon form for the augmented coefficient matrix is What is the solution to the linear system? Select the correct choice below and, if necessary, fill in the answer box(es) in your choice. OA. There is a unique solution, x₁ = x₂ = x3 - (Simplify your answers.) B. There are infinitely many solutions of the form x₁ = x2-x3-t where t is a real number. (Simplify your answers. Type expressions using t as the variable.) 21 OC. There are infinitely many solutions of the form x, .X₂S, X₁t where s and t are real numbers. (Simplify your answer. Type expression using s and t as the variables.) D. There is no solution.
Answers
The solution to the linear system is unique solution which is x₁ = 1/6, x₂ = 3/2, and x₃ = 17/6.
The correct answer is option A.
To solve the given system of linear equations using elementary row operations and back substitution, let's start by representing the augmented coefficient matrix:
[1 -4 5 | 23]
[2 1 1 | 10]
[-3 2 -3 | -23]
We'll apply row operations to transform this matrix into echelon form:
1. Multiply Row 2 by -2 and add it to Row 1:
[1 -4 5 | 23]
[0 9 -9 | -6]
[-3 2 -3 | -23]
2. Multiply Row 3 by 3 and add it to Row 1:
[1 -4 5 | 23]
[0 9 -9 | -6]
[0 -10 6 | -68]
3. Multiply Row 2 by 10/9:
[1 -4 5 | 23]
[0 1 -1 | -2/3]
[0 -10 6 | -68]
4. Multiply Row 2 by 4 and add it to Row 1:
[1 0 1 | 5/3]
[0 1 -1 | -2/3]
[0 -10 6 | -68]
5. Multiply Row 2 by 10 and add it to Row 3:
[1 0 1 | 5/3]
[0 1 -1 | -2/3]
[0 0 -4 | -34/3]
Now, we have the augmented coefficient matrix in echelon form. Let's solve the system using back substitution:
From Row 3, we can deduce that -4x₃ = -34/3, which simplifies to x₃ = 34/12 = 17/6.
From Row 2, we can substitute the value of x₃ and find that x₂ - x₃ = -2/3, which becomes x₂ - (17/6) = -2/3. Simplifying, we get x₂ = 17/6 - 2/3 = 9/6 = 3/2.
From Row 1, we can substitute the values of x₂ and x₃ and find that x₁ + x₂ = 5/3, which becomes x₁ + 3/2 = 5/3. Simplifying, we get x₁ = 5/3 - 3/2 = 10/6 - 9/6 = 1/6.
For more such information on: unique solution
https://brainly.com/question/31028007
#SPJ8
(23 pts) Let X and Y have joint density f XY (x,y)=24xy f XY (x,y)=\ matrix 24xy&x>=0,y>=0,x+y<=1\\ 0&otherwise matrix
Find the marginal density of X / Y
(1)
Answers
To find the marginal density of X/Y, we need to integrate the joint density function fXY(x, y) over the range of Y. By performing the integration, we obtain the marginal density of X/Y as a function of X. The resulting marginal density provides information about the distribution of the ratio X/Y.
The marginal density of X/Y can be obtained by integrating the joint density function fXY(x, y) over the range of Y. In this case, the joint density function is given by:
fXY(x, y) =
24xy if x >= 0, y >= 0, and x + y <= 1
0 otherwise
To find the marginal density of X/Y, we integrate fXY(x, y) with respect to y, while keeping x as a constant. The integration limits for y can be determined based on the given conditions x >= 0, y >= 0, and x + y <= 1. Since y must be non-negative, the lower limit of integration is 0. The upper limit of integration can be determined by the constraint x + y <= 1, which implies y <= 1 - x.
Integrating fXY(x, y) over the range of y, we obtain the marginal density of X/Y as follows:
fX/Y(x) = ∫[0 to (1 - x)] 24xy dy
Evaluating the integral, we have:
fX/Y(x) = 24x * ∫[0 to (1 - x)] y dy
= 24x * [(y^2)/2] evaluated from 0 to (1 - x)
= 12x * (1 - x)^2
The resulting marginal density fX/Y(x) represents the distribution of the ratio X/Y. It provides information about the likelihood of different values of X/Y occurring. The shape of the distribution can be further analyzed to understand the characteristics of the random variable X/Y.
To learn more about function click here: brainly.com/question/30721594
#SPJ11
what situations would solve by graphing be your preferred choice? Give an example.
In what situations would solve by substitution be your preferred choice? Give an example.
In what situations would solve by elimination be your preferred choice? Give an example.
Write a linear system that can be solved by any of the three methods.
Answers
Answer:
1) The solve by graphing will the preferred choice when the equation is complex to be easily solved by the other means
Example;
y = x⁵ + 4·x⁴ + 3·x³ + 2·x² + x + 3
2) Solving by substitution is suitable where we have two or more variables in two or more (equal number) of equations
2x + 6y = 16
x + y = 6
We can substitute the value of x = 6 - y, into the first equation and solve from there
3) Solving an equation be Elimination, is suitable when there are two or more equations with coefficients of the form, 2·x + 6·y = 23 and x + y = 16
Multiplying the second equation by 2 and subtracting it from the first equation as follows
2·x + 6·y - 2×(x + y) = 23 - 2 × 16
2·x - 2·x + 6·y - 2·y = 23 - 32
0 + 4·y = -9
4) An example of a linear system that can be solved by all three methods is given as follows;
2·x + 6·y = 23
x + y = 16
Step-by-step explanation:
angle <1 and angle <2 are complementary angles. The measure of angle <1 is 42 degrees. The measure of angle <2 is 4x degrees. Find the value of x. The figure is not drawn to scale.
Answers
The value of x is 12.
we have, <1 = 42 degree
<2 = 4x degree
As, <1 and <2 are Complementary Angle.
So, the sum of <1 and <2 will be 90 degree
<1 + <2 = 90
42 + 4x = 90
4x = 90-42
4x = 48
x= 48/4
x= 12
Thus, the value of x is 12.
Learn more about Complementary Angle here:
https://brainly.com/question/5708372
#SPJ1
Alice's wholesale reported its sales in the year ended 30th June 2019as RM511,000. If her trade receivables on 30th June 2019 were RM63,000, calculate her receivable days. 45 days 30 days 25 days 60 days
Answers
To calculate the receivable days, divide the trade receivables (RM63,000) by the average daily sales (RM1,400) to get approximately 45 days.
To calculate the receivable days, we need to determine the average daily sales and then divide the trade receivables by that figure.
First, we calculate the average daily sales by dividing the total sales by the number of days in the year:
Average daily sales = Total sales / Number of days
Since the year ended on 30th June 2019, there are 365 days in total.
Average daily sales = RM511,000 / 365 = RM1,400
Next, we divide the trade receivables by the average daily sales to find the receivable days:
Receivable days = Trade receivables / Average daily sales
Receivable days = RM63,000 / RM1,400 ≈ 45 days
Therefore, Alice's receivable days on 30th June 2019 is approximately 45 days.
To learn more about average daily sales click here brainly.com/question/15711496
#SPJ11
Of the following, which is the solution to 2x2 + 3x = −5?
Answers
Answer:
Step-by-step explanation:
Nothing to choose from??/
But 2x^2+3x=-5 is
- 3± i√31 / 4
Answer:
\(\frac{-3+-i\sqrt{31} }{4}\)
ye
Triangles ABC and XYZ are similar. Find side x. Triangle ABC: 12, 18, 9. Triangle XYZ: 4, x,
Answers
The value of x is 6 using similarity of triangle.
What is Similarity of triangle ?If two triangles have an equal number of corresponding sides and an equal number of corresponding angles, then they are comparable.
Similar figures are described as items with the same shape but varying sizes, such as two or more figures. A hula hoop and the wheel of a bicycle are two examples of things whose forms are similar to one another.
Properties:
Despite having the same form, each might have different sizes.There are no matching angles that are not equal.Similar equivalent side ratios exist.side AB is proportional to side XY
side AC is proportional to side XZ
Since we know side AB and side XY are proportional to each other, if we divide side AB by side XY, we can find the size difference...
12 / 4 = 3
The smaller triangle is 3 times smaller than the bigger triangle so we can find side XZ by dividing side AC by 3...
18 / 3 = 6
x = 6.
To learn more about Similarity of triangle refer to :
https://brainly.com/question/23575326
#SPJ1

HEEEEELPPPPP
Find an equation of the line that satisfies the given conditions.
y-intercept 1; parallel to the line 3x + 4y + 9 = 0
Answers
Answer:
y = -3/4x + 1
Step-by-step explanation:
lines are parallel if their slopes are equal
we can find the slope of 3x + 4y + 9 = 0 by changing it into 'y = mx + b' or slope-intercept form:
3x + 4y = -9
4y = -3x - 9
y = -3/4x - 9/4
slope = -3/4
y-intercept = 1
therefore, answer is y = -3/4x + 1
a grain silo consists of a cylindrical main section and a hemispherical roof of the total volume of the silo (including the part inside the roof section) is 10,000 find.the.cylindrical part is 30 ft tall, what is the radius of the silo, correct to the nearest tenth of a foot?
Answers
The radius of the silo which is in the shape of cylinders and spheres , correct to the nearest tenth of a foot, is approximately 10.3 feet.
To find the radius of the silo, we need to determine the radius of the cylindrical section.
The volume of the cylindrical section can be calculated using the formula:
\(V_{cylinder} = \pi * r^2 * h\)
where \(V_{cylinder}\) is the volume of the cylindrical section, r is the radius of the cylindrical section, and h is the height of the cylindrical section.
Given that the cylindrical section is 30 ft tall, we can rewrite the formula as:
\(V_{cylinder} = \pi * r^2 * 30\)
To find the radius, we can rearrange the formula:
\(r^2 = V_{cylinder} / (\pi * 30)\)
Now, we can substitute the total volume of the silo, which is 10,000 cubic feet, and solve for the radius:
\(r^2 = 10,000 / (\pi * 30)\)
Simplifying further:
\(r^2 = 106.103\)
Taking the square root of both sides, we find:
\(r = \sqrt{106.103} = 10.3\)
Therefore, the radius of the silo which is in the shape of cylinders and spheres , correct to the nearest tenth of a foot, is approximately 10.3 feet.
Learn more about cylinders and spheres here.
https://brainly.com/question/23947152
#SPJ4
anyone know the answer?

Answers
Step-by-step explanation:
\( {9}^{ \frac{ - 1}{2} } \\ {3}^{2 \times - \frac{1}{2} } \\ {3}^{ - 1} \\ \frac{1}{3} \)
Now for another
\( {27}^{ \frac{ - 2}{3} } \\ {3}^{3 \times \frac{ - 2}{3} } \\ {3}^{ - 2} \\ \frac{1}{9} \)
Hope it will help :)❤
Which of the following expressions is equivalent to 2x + 3?
6(2)x
8(2)x
the quantity 2 to the power of x end quantity over 6
the quantity 2 to the power of x end quantity over 8
Answers
The expressions which is equivalent to 2x + 3 would be 4x + 6.
What are equivalent expressions?Those expressions who might look different but their simplified forms are same expressions are called equivalent expressions. To derive equivalent expressions of some expression, we can either make it look more complex or simple. Usually, we simplify it.
We need to find the expressions which is equivalent to 2x + 3
Thus, we will Use the Distribute Property of Multiplication by multiplying the number outside the parenthesis with the numbers inside.
Let the expression be multiplying by 2 then;
2(2x + 3)
4x + 6
Hence, we can say that the expressions which is equivalent to 2x + 3 would be 4x + 6.
Learn more about expression here;
https://brainly.com/question/14083225
#SPJ1
as a television executive, you have been given 9 shows to choose from to run during your prime time slots each week. if you have 7 time slots, how many ways can you create the schedule for the week?
Answers
I can create the schedule 181440 ways for the week.
What are permutation and combination?A permutation is an arrangement of things where order matters, AB and BA are two different permutations.
The combination is a selection of things where order does not matter, AB and BA are the same combinations.
Given, As a television executive, you have been given 9 shows to choose from and you have 7-time slots.
Therefore, The first slot can be filled by 9 different shows, And the next can be done is 8 different shows.
Continuing this way we can fill 7 slots with 9 different shows as,
9×8×7×6×5×4×3 ways.
= 181440 ways.
It is a permutation so we can also have calculated as, \(^9P_7 = \frac{9!}{(9-2)!}\) ways.
learn more about permutation and combination here :
https://brainly.com/question/28720645
#SPJ1
What is \redD{\text{A}}Astart color #e84d39, start text, A, end text, end color #e84d39 rounded to the nearest ten? What is \redD{\text{A}}Astart color #e84d39, start text, A, end text, end color #e84d39 rounded to the nearest hundred?
Answers
Answer:
What? Retype the question below and ill answer it, but this isnt answerable.
Step-by-step explanation:
What is \redD{\text{A}}Astart color #e84d39, start text, A, end text, end color #e84d39 rounded to the nearest ten? What is \redD{\text{A}}Astart color #e84d39, start text, A, end text, end color #e84d39 rounded to the nearest hundred?
Like what kind of language is this ;--;
What is another way to write -8+5?
Answers
Answer:
5-8
Step-by-step explanation:
you just had to move the 8 over
"Determine the values of the variables using BIG M Method (manual
solution)
pls show each tableau with the M variables
Given: Maximize Z= -2x1 + x2 - 4x3 + 3x4 Subject to: X1 + x2 + 3x3 + 2x4≤4
x1 - x3 + x4≥-1
2x1 + x2 ≤ 2
x1 + 2x2 + x3 + 2x4=2 X1, X2, X3, X4≥ 0"
Answers
To obtain the following tableau, we pivot around the element at the intersection of the x1 column and the x6 row:
| BV | x1 | x2 | x3 | x4 | x5 | x6 | x7
What is variable?A variable (from the Latin variabilis, "changeable") is a mathematical symbol. A variable can be a number, a vector, a matrix, a function, its argument, a set, or an element of a set.
To solve the given linear programming problem using the Big M method, we need to convert the problem into standard form by adding slack, surplus, and artificial variables as needed. Then, we use the simplex algorithm to iteratively improve the solution until we reach an optimal solution.
Let's first write the problem in standard form by introducing slack and artificial variables as follows:
Maximize Z = -2x1 + x2 - 4x3 + 3x4
Subject to:
x1 + x2 + 3x3 + 2x4 + x5 = 4
x1 - x3 + x4 - x6 = -1
2x1 + x2 + x7 = 2
x1 + 2x2 + x3 + 2x4 = 2
where x5, x6, x7 are slack and artificial variables.
We can see that the problem is infeasible because the last equation is inconsistent with the second equation. To make the problem feasible, we need to introduce artificial variables for the second equation and modify the objective function to penalize their use. This leads us to the following modified problem:
Maximize Z = -2x1 + x2 - 4x3 + 3x4 - M(x6 + x8)
Subject to:
x1 + x2 + 3x3 + 2x4 + x5 = 4
x1 - x3 + x4 + x6 - x8 = -1
2x1 + x2 + x7 = 2
x1 + 2x2 + x3 + 2x4 = 2
where x5, x6, x7, x8 are slack and artificial variables, and M is a large positive constant.
Now, we can construct the initial simplex tableau as follows:
| BV | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | RHS |
|----|----|----|----|----|----|----|----|----|-----|
| x5 | 1 | 1 | 3 | 2 | 1 | 0 | 0 | 0 | 4 |
| x6 | 1 | 0 | -1 | 1 | 0 | 1 | 0 | -1 | -1 |
| x7 | 2 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 2 |
| x8 | 1 | 1 | 2 | 1 | 0 | 0 | 0 | -1 | 2 |
| Z | -2 | 1 | -4 | 3 | 0 | M | 0 | -M | 0 |
The column for the objective function includes the coefficients of the original variables and the artificial variables, with the artificial variables having a coefficient of M in the objective function.
To perform the simplex algorithm, we select the most negative coefficient in the bottom row, which corresponds to x1, as the entering variable. We then select the row with the smallest nonnegative ratio of the RHS to the coefficient of the entering variable, which corresponds to x6, as the leaving variable. We pivot around the element in the intersection of the x1 column and the x6 row to obtain the next tableau:
| BV | x1 | x2 | x3 | x4 | x5 | x6 | x7
Learn more about variable on:
https://brainly.com/question/383055
#SPJ11
1. Write an equation (y = a/x) that shows this relationship. Use y as your number of tacos and x as the price 2. How many tacos would you buy if they were $2.40 each ? 3. What would the price of a taco be if you bought 16 tacos? Your answer
Answers
Answer:
The equation that shows the relationship between the number of tacos (y) and the price (x) is: y = a/x If we use y as the number of tacos and x as the price of one taco, we can substitute the given values to find a. Let's assume that you would buy 5 tacos when the price is $1.20 each. Then we have: 5 = a/(1.20) Multiplying both sides by 1.20, we get: a = 6 So the equation becomes: y = 6/x Now we can answer the other questions: 2. If the price of a taco is $2.40 each, we can substitute x = 2.40 into the equation to find y: y = 6/2.40 = 2.5 So you would buy 2.5 tacos, whichDomain represents which of the following?
A. slope
B. x values
C. y values
D. maximum
Answers
Answer:
b
Step-by-step explanation:
20)
A single card is chosen at random from a standard deck of 52 playing cards. Which BEST describes the probability of drawing a king
from the deck?
Answers
The best description of the probability of drawing a king from the deck is 1 out of 13, or 1/13.
The probability of drawing a king from a standard deck of 52 playing cards can be determined by dividing the number of favorable outcomes (number of kings) by the total number of possible outcomes (total number of cards in the deck).
In a standard deck, there are 4 kings (one king for each suit: hearts, diamonds, clubs, and spades). Therefore, the number of favorable outcomes is 4.
The total number of possible outcomes is 52 (the total number of cards in the deck).
So, the probability of drawing a king is:
Probability = Number of favorable outcomes / Total number of possible outcomes
Probability = 4 / 52
Simplifying the fraction gives us:
Probability = 1 / 13
Know more about probabilityhere:
https://brainly.com/question/31828911
#SPJ11
Find an equation for the linear function g(x) which is perpendicular to the line 7x - 6y = 18 and intersects the line 7x - 6y = 18 at x = 30. g(x) =
Answers
y = (7/6)x - 3
The slope of the given line is 7/6. To find the equation for the linear function g(x) that is perpendicular to the line 7x - 6y = 18 and intersects it at x = 30, we first need to find the slope of the given line.
1. Find the slope of the line 7x - 6y = 18:
To do this, we need to write the equation in the slope-intercept form (y = mx + b), where m represents the slope.
7x - 6y = 18
-6y = -7x + 18
y = (7/6)x - 3
The slope of the given line is 7/6.
2. Find the slope of the perpendicular line:
Perpendicular lines have slopes that are negative reciprocals of each other. So, the slope of the perpendicular line, g(x), is:
m_g(x) = -6/7
3. Find the y-coordinate of the intersection point:
We know that the line g(x) intersects the given line at x = 30. Plug x = 30 into the given line equation to find the corresponding y-coordinate.
y = (7/6)(30) - 3
y = 35
The intersection point is (30, 35).
4. Find the equation for g(x):
Now that we have the slope and a point on the line g(x), we can use the point-slope form (y - y1 = m(x - x1)) to find the equation.
y - 35 = (-6/7)(x - 30)
This is the equation for g(x) that is perpendicular to the line 7x - 6y = 18 and intersects it at x = 30.
Learn more about perpendicular line here:
https://brainly.com/question/18271653
#SPJ11
PLEASE HELPPPPL!!!
Find the solution to the system of equations by graphing.
y = -3x + 1
y = X-7

Answers
Answer:
(0,1) (0.333,0)
(7,0)
m=1
Step-by-step explanation:
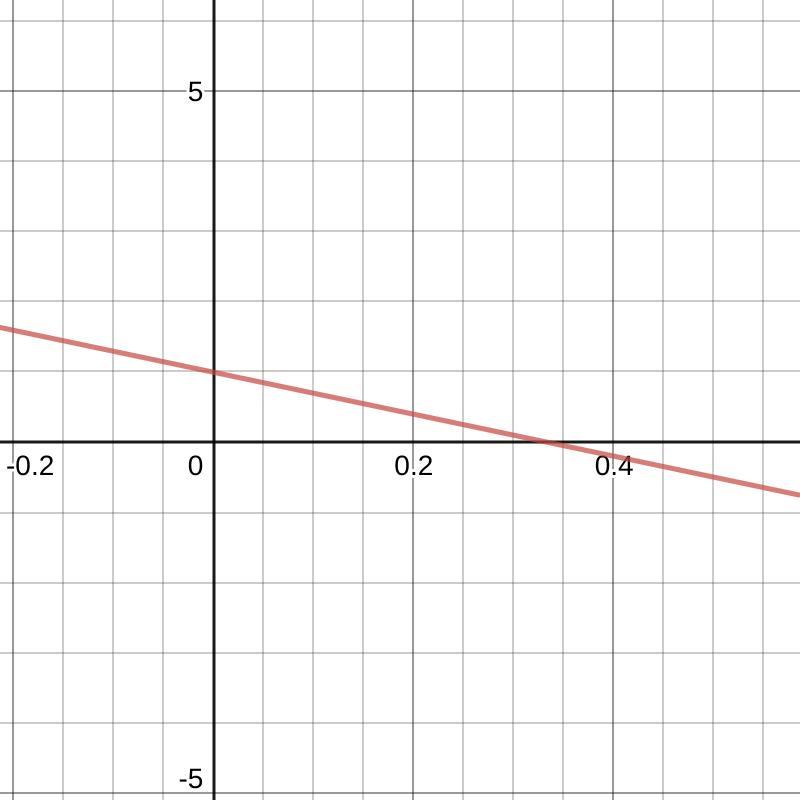

Find an angle 0 coterminal to 801°, where 0° < 0 < 360°.
Answers
Answer:
\(\alpha' = 81^{\circ}\)
Step-by-step explanation:
Angle is periodical function, so that following condition is satisfied:
\(\alpha = n \cdot 360^{\circ}\)
\(n = \frac{801^{\circ}}{360^{\circ}}\)
\(n = 2.225\)
The position of the coterminal angle is:
\(n' = 2.225 - 2\)
\(n' = 0.225\)
\(\alpha' = n' \cdot 360^{\circ}\)
\(\alpha' = (0.225)\cdot (360^{\circ})\)
\(\alpha' = 81^{\circ}\)
a dye is injected into the pancreas during a certain medical procedure. a physician injects 0.3 grams of the dye, and a healthy pancreas will secrete 4% of the dye each minute. predict the amount of dye remaining, to the nearest hundredth of a gram, in a healthy pancreas 30 minutes after the injection.
Answers
The estimated quantity of dye left in a healthy pancreas 30 minutes after the injection, rounded to the closest hundredth of a grams, is 0.07 grams.
As per the question given,
After the dye is injected, a healthy pancreas will secrete 4% of the remaining amount of dye each minute. Let's use exponential decay to model the amount of dye remaining in the pancreas over time.
The amount of dye remaining after t minutes can be expressed as:
R(t) = 0.3 * (1 - 0.04)^t
We want to find the amount of dye remaining after 30 minutes, so we can substitute t=30 into the equation and calculate:
R(30) = 0.3 * (1 - 0.04)^30
R(30) = 0.3 * (0.96)^30
R(30) = 0.3 * 0.2312
R(30) = 0.0694
Rounding to the nearest hundredth of a gram, the predicted amount of dye remaining in a healthy pancreas 30 minutes after the injection is 0.07 grams.
For such more questions on Dye
https://brainly.com/question/28882250
#SPJ4
Answer:
0.09 g
Step-by-step explanation:
You want to know the amount remaining of 0.3 g of dye after 30 minutes if the amount decreases by 4% per minute.
Exponential functionThe amount can be modeled by the exponential function ...
q = a·b^t
where q is the quantity remaining, 'a' is the initial quantity, b is the growth factor per minute, and t is the number of minutes.
The growth factor is related to the growth rate by ...
b = 1 + growth rate
ApplicationHere, the growth rate is -4% per minute, so the growth factor is ...
b = 1 +(-0.04) = 0.96
The initial quantity is 0.3 grams, so the remaining quantity after 30 minutes is ...
q = 0.30·0.96^30 ≈ 0.08816 ≈ 0.09 . . . . grams
The amount of dye remaining after 30 minutes is predicted to be 0.09 g.
<95141404393>

Use the formula to find the volume of the figure. Show your work.

Answers
Hello !
Answer:
\(\boxed{\sf V{cone} \approx 2408.55 m^3}\)
Step-by-step explanation:
To find the volume of a cone with the radius of its base and its height, we will apply the following formula:
\( \sf V{cone} = \dfrac{\pi \times r^2 \times h}{3} \)
Where r is the radius of its base and h is its height.
Given:
r = 10 mh = 23 mLet's substitute our values into the formula:
\(\sf V{cone} = \dfrac{\pi (10)^2(23)}{3} = \dfrac{2300\pi}{3} \ \ \\\boxed{\sf V{cone} \approx 2408.55 m^3}\)
Have a nice day ;)
help please :( please just do 1-7

Answers
1. Liquids have a definite volume, but take the shape of the container.
2.A physical property is a characteristic of a substance that can be observed or measured without changing the identity of the substance. Physical propertiesinclude color, density, hardness, and melting and boiling points. A chemical property describes the ability of asubstance to undergo a specificchemical chang
Answer: 1- liquid
2- chemical property A chemical property is any of a material's properties that becomes evident during, or after, a chemical reaction
physical property- A physical property is any property that is measurable, whose value describes a state of a physical system. The changes in the physical properties of a system can be used to describe its changes between momentary states
3- melting point and density
4- solids are closer together; more compacted, move faster
liquids are a little bit far apart; still close together and move a little slower
gases are fart apart; move slower
5- flammability
6- because they move slower and are more far apart then liquids and solids
7- I can't see the table :)
Step-by-step explanation:
find the value s of x and y

Answers
Answer:
x = 180-35 = 145
y = 35
Hope it helps
please help due in 20 minutes

Answers
In ∆PTQ
Apply Pythagorean theorem
\(\\ \tt\hookrightarrow PT^2=PQ^2+QT^2\)
\(\\ \tt\hookrightarrow PT^2=15.4^2+9.3^2=323.16\)
\(\\ \tt\hookrightarrow PT=17.9\)
In ∆TRQ
\(\\ \tt\hookrightarrow tan44.4=\dfrac{QT}{TR}=\dfrac{9.3}{TR}\)
\(\\ \tt\hookrightarrow 0.9=\dfrac{9.3}{TR}\)
\(\\ \tt\hookrightarrow TR=\dfrac{9.3}{0.9}=10.3\)
PR=PT+TR=10.3+17.9=28.2cmNow
Area:-
\(\\ \tt\hookrightarrow 1/2bh\)
\(\\ \tt\hookrightarrow 1/2(28.2)(9.3)\)
\(\\ \tt\hookrightarrow 14.1(9.3)\)
\(\\ \tt\hookrightarrow 131.13cm^2\)
Find two nonnegative numbers x and y such that xy = 72 and 9x + 2y is minimized.
x= ____
y =______
Answers
two nonnegative numbers x and y that satisfy xy = 72 and minimize 9x + 2y are x = 4 and y = 18.
To solve this problem, we can use the technique of optimization by setting up an equation for 9x + 2y and then using the given condition xy = 72 to eliminate one of the variables.
First, let's express 9x + 2y in terms of just one variable:
9x + 2y = 9x + 2(72/x) = 9x + 144/x
Now we need to minimize this expression. To do so, we can take the derivative with respect to x and set it equal to zero:
d/dx (9x + 144/x) = 9 - 144/x^2 = 0
Solving for x, we get:
x^2 = 144/9
x^2 = 16
x = 4 (since we want a nonnegative value for x)
Substituting this value of x into the equation xy = 72, we get:
4y = 72
y = 18
Therefore, the two nonnegative numbers x and y that satisfy xy = 72 and minimize 9x + 2y are x = 4 and y = 18.
learn more about 'minima':https://brainly.com/question/31389382
#SPJ11
On Monday, 184 students went on a trip to the zoo. All 4 buses were filled and 8 students had to travel in cars. How many students were in each bus ? show work
Answers
We have the following:
In this case, the first thing is to divide all the students into 4 groups, just like this
\(\frac{184}{4}=46\)Then, since 8 students left in cars, now we must take the equal amount from each group, therefore
\(\frac{8}{4}=2\)From each group we took 2 people, which means that 44 students would then leave each bus (46-2)