Susie has $95 to spend on renting snorkeling gear at the beach. There is a $15 flat service fee to rent the snorkeling gear along with an $8 charge for each hour the gear is used. The inequality that can be used to find the number of hours Susie can rent the snorkeling gear is 15 + 8h ≤ 95. Calculate the maximum number of hours Susie can rent the snorkeling gear.
Answers
Answer:
10 hours
Step-by-step explanation:
We can actually solve this problem simply as if it were an equation instead of an inequality. We have:
15 + 8h ≤ 95
Subtract 15 from both sides:
8h ≤ 95 - 15
8h ≤ 80
Divide by 8 from both sides:
h ≤ 80/8
h ≤ 10
So, the number of hours cannot exceed 10, which means the maximum number of hours Susie can rent is 10 hours.
Answer:
the answer is attached to the picture

Related Questions
Three students made claims about y.Each student has provided his or her work to support their claim, as shown below.analyze the student's work and identify which part of his or her claim is correct or incorrect? Select TWO that apply.

Answers
C and E
1) Let's evaluate that so we can find out the answers:
\(\begin{gathered} y^{\frac{3}{2}}=(y^{\frac{1}{3}}\cdot y^{\frac{1}{3}}) \\ y^{\frac{3}{2}}\ne y^{\frac{1+1}{3}}\Rightarrow y^{\frac{3}{2}}\ne y^{\frac{2}{3}} \end{gathered}\)So Student 1 has come to a false conclusion.
• Student 2
\(\begin{gathered} y^{\frac{3}{2}}=(y\cdot y\cdot y)^{\frac{1}{2}}\Rightarrow y^{\frac{3}{2}}=(y^3)^{\frac{1}{2}}\Rightarrow y^{\frac{3}{2}}=y^{\frac{3}{2}} \\ (\sqrt[]{y\cdot y\cdot y})=(y^{\frac{3}{2}})=(\sqrt[]{y^3}) \end{gathered}\)Note that we can add the exponents of a product of power with the same exponent. Also, rational exponents indicate a radical.
So Student 2 has come to a True conclusion
• Student 3
\(\begin{gathered} y^{\frac{3}{2}}=(y^{\frac{1}{2}+\frac{1}{2}+\frac{1}{2}})\Rightarrow y^{\frac{3}{2}}=y^{\frac{3}{2}} \\ (\sqrt[]{y}\cdot\sqrt[]{y}\cdot\sqrt[]{y})=(\sqrt[]{y}^3)\text{ =}y^{\frac{3\times1}{2}}=y^{\frac{3}{2}} \end{gathered}\)Since by the exponents' property the sum of the exponents within a product of same base powers and rational exponents rewritten as radicals, we can state that Studen t 3 has come up to a true conclusion.
3) Hence, the answers are:
C and E
Why is it important to know the background of a poet.
Answers
Answer:
To understand their poems better
Step-by-step explanation:
First you have a general knowledge on why the author made the poem
Second you now have more info to use in order to understand the poems
Third is the same reason why there are people in history books.
if the pile contains only 15 quarters and only 20 dimes but at least 30 of each other kind of coin, how many collections of 30 coins can be chosen?
Answers
The number of ways to choosing coins with at least 15 quarters and 20 dimes is 4354.
In the given question, if the pile contains only 15 quarters and only 20 dimes but at least 30 of each other kind of coin, then we have to find the collections of 30 coins can be chosen.
Number of coins only of quarters = 15
Number of coins only of dimes = 20
The number of ways to choosing coins with at least 15 quarters and 20 dimes= Total- \((^{18}C_{3}+^{13}C_{3})\)
The number of ways to choosing coins with at least 15 quarters and 20 dimes= \(^{33}C_{3}-(^{18}C_{3}+^{13}C_{3})\)
Using \(^{n}C_{r}=\frac{n!}{r!(n-r)!}\)
The number of ways to choosing coins with at least 15 quarters and 20 dimes= \(\frac{33!}{3!(33-3)!}-(\frac{18!}{3!(18-3)!}+\frac{13!}{3!(13-3)!})\)
The number of ways to choosing coins with at least 15 quarters and 20 dimes= \(\frac{33!}{3!30!}-(\frac{18!}{3!15!}+\frac{13!}{3!10!})\)
Simplifying
The number of ways to choosing coins with at least 15 quarters and 20 dimes= \(\frac{33\times32\times31\times30!}{3\times2\times1\times30!}-(\frac{18\times17\times16\times15!}{3\times2\times1\times15!}+\frac{13\times12\times11\times10!}{3\times2\times1\times10!})\)
The number of ways to choosing coins with at least 15 quarters and 20 dimes= 11×16×31-(3×17×16+13×2×11)
The number of ways to choosing coins with at least 15 quarters and 20 dimes= 5456-(816+286)
The number of ways to choosing coins with at least 15 quarters and 20 dimes= 5456-1102
The number of ways to choosing coins with at least 15 quarters and 20 dimes= 4354
If the pile contains only 15 quarters and only 20 dimes but at least 30 of each other kind of coin, the number of ways to choosing coins with at least 15 quarters and 20 dimes is 4354.
To learn more about quarters and dimes link is here
brainly.com/question/6500943
#SPJ4
The breaking strength of a rivet has a mean value of 10,100 psi and a standard deviation of 499 psi. (a) What is the probability that the sample mean breaking strength for a random sample of 40 rivets is between 10,000 and 10,300? (Round your answer to four decimal places.) (b) If the sample size had been 15 rather than 40, could the probability requested in part (a) be calculated from the given information? Explain your reasoning O Yes, the probability in part (a) can still be calculated from the given information O No, n should be greater than 30 in order to apply the Central Limit Theorem. O No, n should be greater than 20 in order to apply the Central Limit Theorem. O No, n should be greater than 50 in order to apply the Central Limit Theorem. You may need to use the appropriate table in the Appendix of Tables to answer this question.
Answers
the probability that the sample mean breaking strength for a random sample of 40 rivets is between 10,000 and 10,300 P(10000 ≤ x ≤ 10300) = 0.54
We would assume a normal distribution for the breaking strength of a rivet. We would apply the formula for normal distribution which is expressed as
z = (x - µ)/σ/√n
Where
n = number of samples
x = Breaking strengths of rivet.
µ = mean breaking strength
σ = standard deviation
From the information given,
µ = 10,100 psi
σ = 499 psi
n = 40
The probability that the sample mean breaking strength for a random sample of 40 rivets is between 10000 and 10,300 is expressed as
P(10000 ≤ x ≤ 10300)
For x = 10000,
z = (10000 - 10100)/499/√40 = - 0.13
Looking at the normal distribution table, the probability corresponding to the z score is 0.45
For x = 10300,
z = (10300 - 10100)/499/√40 = 2.54
Looking at the normal distribution table, the probability corresponding to the z score is 0.99
Therefore,
P(10000 ≤ x ≤ 10300) = 0.99 - 0.45 = 0.54
learn more about of probability here
https://brainly.com/question/15248399
#SPJ4
If the thickness of an absorber is 1.5 cm and 36.45% of a beam is attenuated by the absorber, what is the tenth-value layer? 7.61 cm 2.78 cm 3.89 cm None of the given options. 15 pts 9.21 cm
Answers
4.1715 cm is the tenth-value layer. So, none of the given options (7.61 cm, 2.78 cm, 3.89 cm, 9.21 cm) matches the calculated value of the tenth-value layer.
Here, we have,
To determine the tenth-value layer, we need to find the thickness of the absorber required to reduce the intensity of the beam to one-tenth (10%) of its original value.
Given that the thickness of the absorber is 1.5 cm and 36.45% of the beam is attenuated, we can set up the following equation:
(1 - 36.45%)ⁿ = 10%
Here, 'n' represents the number of layers of absorber required to reach the tenth-value layer. Since we're looking for the thickness of the tenth-value layer, we need to solve for 'n' in the equation.
Let's calculate 'n':
(1 - 0.3645)ⁿ = 0.1
0.6355ⁿ = 0.1
Taking the natural logarithm (ln) of both sides:
n * ln(0.6355) = ln(0.1)
n = ln(0.1) / ln(0.6355)
Using a calculator, we find that n ≈ 2.781
Now, we can determine the thickness of the tenth-value layer by multiplying 'n' by the thickness of each absorber layer:
Tenth-value layer thickness = n * 1.5 cm
Tenth-value layer thickness ≈ 2.781 * 1.5 cm
Calculating this, we find that the approximate thickness of the tenth-value layer is 4.1715 cm.
Therefore, none of the given options (7.61 cm, 2.78 cm, 3.89 cm, 9.21 cm) matches the calculated value of the tenth-value layer, which is approximately 4.1715 cm.
To learn more on Logarithm click:
brainly.com/question/10418010
#SPJ4
Kate and Jalon are scuba diving. Kate is 9
feet below the surface and Jalon is 16 feet
below the surface. If Kate descends 8 more
feet and Jalon rises 4 feet, find the vertical
distance between them.
Answers
Answer:
5 feet
Step-by-step explanation:
Kate would then be 17 feet under
Jalon would then be 12 feet under
Subtract.
Determinestudent submitted image, transcription available belowwhenstudent submitted image, transcription available belowis a chi-square random variable with 26 degrees of freedom
Answers
A chi-square random variable with 26 degrees of freedom follows the chi-square distribution, which is commonly used in statistical analyses and hypothesis testing.
The chi-square distribution is a probability distribution that is commonly used in statistical inference and hypothesis testing. It arises in various statistical analyses, particularly when dealing with categorical or count data.
The chi-square distribution is characterized by its degrees of freedom, which determine the shape and characteristics of the distribution. In this case, the random variable X is said to follow a chi-square distribution with 26 degrees of freedom.
The degrees of freedom in a chi-square distribution represent the number of independent pieces of information used to estimate a parameter. In the context of the chi-square test, degrees of freedom are typically associated with the number of categories or groups being compared.
By knowing that X is a chi-square random variable with 26 degrees of freedom, we can utilize the properties and formulas associated with this distribution to perform calculations and make statistical inferences, such as calculating probabilities, conducting hypothesis tests, or estimating confidence intervals.
Learn more about chi-square distribution here:
https://brainly.com/question/30764634
#SPJ11
an automated weight monitor can detect underfilled cans of beverages with probability 0.98. what is the probability it fails to detect an underfilled can for the first time when it encounters the 10th underfilled can?
Answers
The probability it fails to detect an underfilled can for the first time when it encounters the 10th underfilled is \(0.01667496\).
What is probability?
Probability is defined as the possibility of an event to occur.
An automated weight monitor can detect underfilled cans of beverages with probability \(0.98\)
Thus probability of success will be \(p=0.98\)
So probability of failure \(q=1-p=1-0.98=0.02\)
To find the first wrong detection happening on the tenth trial the first nine trials must be success followed by failure in the tenth trial.
Thus, required probability \(=p^9q^1=(0.98)^9(0.02)=0.01667496\)
Hence the probability it fails to detect an underfilled can for the first time when it encounters the 10th underfilled is \(0.01667496\).
To know more about probability from given link,
https://brainly.com/question/24756209
#SPJ4
HELP ITS URGENT. PART 1#.
Allenbright's Electronics is having a "25% OFF" sale. If a radio is SALE priced at $135, what is its regular price?
3. Draw a picture or chart that shows the information and the question.
1
Select the correct answer.
A.
$168.75
B.
$101.25
C.
$180.00
D.
$33.75
Answers
Answer:
A.168.75
Step-by-step explanation:
Discount = Original Price x Discount %/100
Discount = 135 × 25/100
Discount = 135 x 0.25
You save = $33.75
now add that discount to the 135 to find out the original price which is 168.75
Answer:
A=$168.75
Step-by-step explanation:
discount =original price*discount/100
D=$135*25/100
D=$135*0.25
D=$33.75
Total price=$135+$33.75
$165.75
Sydney spends a winter day recording the temperature once every three hours for science class. At 9 am, the temperature was -12.3°F. Between 9am and noon, the temperature rose 12°F. Between noon and 3pm, the temperature went up 11.5°F. Between 3pm and 6pm, the temperature dropped 16.3°F. What was the temperature at 6pm?
Answers
The temperature at 6pm was of -5.1ºF.
This problem can be solved by using system of equations.
A system of equations means when there are two or more variables that are related, and equations are made to find the values of each variable of the problem.
It is given that at 9 am, the temperature was -12.3°F. Between 9am and the noon, the temperature rose 12°F. So, the temperature at noon was of -12.3 + 12 = -0.3ºF.
Also, between the noon and 3pm, the temperature went up 11.5°F. So, at 3 pm, the temperature was of -0.3 + 11.5 = 11.2 ºF.
Further, between 3pm and 6pm, the temperature dropped 16.3°F.So, the temperature at 6 pm was of 11.2 - 16.3 = -5.1 ºF.
Hence, the temperature at 6pm was -5.1°F
To know more about system of equations - https://brainly.com/question/24065247
#SPJ1
13 people on a softball team show up for a game. how many ways are there to choose 10 players to take the field? (you must provide an answer before moving to the next part.)
Answers
858 combinations are there to choose 10 players to take the field.
Pick 10 people from 13,
\(C^{13} _{10}\) = \((^{13} _{2} )\)
Splitting the combination,
\(C^{13} _{10}\) = (13 × 12 × 11) ÷ 2
\(C^{13} _{10}\) = 1716 ÷ 2
\(C^{13} _{10}\) = 858 ways to pick the 10 to play.
There are 858 different methods to select 10 players to take the pitch.
The permutations of a set are the vaguely defined community of its members in arrangement or linear order, or the permutation of its components if the set is already collected. The act or procedure of adjusting the linear ordering of a sorted set is often named "permutation".
Read more about permutation and combination at
https://brainly.com/question/13945389?referrer=searchResults
#SPJ4
Jack is at the zoo looking up at a monkey
sitting on top of a pole. If Jack is standing 24
feet from the foot of the pole and the angle of
elevation from Jack to the top of the pole is 23°.
Find the height of the pole.
Answers
The height of the pole at which the monkey is at the top is 10.2 feet.
Trigonometric ratioTrigonometric ratio is used to show the relationship between the angles and sides of a right angled triangle.
Let h represent the height of the pole, hence using trigonometric ratio:
tan(23) = h/24
h = 10.2 feet
The height of the pole at which the monkey is at the top is 10.2 feet.
Find out more on Trigonometric ratio at: https://brainly.com/question/4326804
Find AC (Round to the nearest tenth) PLS HURRY

Answers
Answer:
Does the answer help you?

What i 464 divided by 60 with a remainder?
(trying to figure out how many hour i 464 minute)
Answers
When we divide the 464 by 60 we get the following remainder in our answer that is 44.
What do math remainders mean?The Remainder is the name for the value that is left behind after division. If an amount (reward) cannot be divided completely with another number, we are left with only a meaning (divisor). The remaining is the name for this amount. For instance, 10 is not precisely divisible by 3. We can calculate 3 x 3 = 9 because that is the closest value.
Briefing :7.733333333333333
=7 44/60 ⇔ 7 R 44
464 divided by 60
=7 with a remainder of 44
Here, we provide you the outcome of the dividing with remainder, often known as the Euclidean division, along with a brief explanation of the following terms:
464 divide by 60 yields a quotient and residual of 7 R 44.
464 is the dividend & 60 is the divisor; the division (numeric division) of 464/60 is 7; the remainder ("left over") is 44.
To know more about Remainder visit :
https://brainly.com/question/23148931
#SPJ4
A test has ____ total questions for a total of ____ points. There are two question types: a true/false question is worth ____ points and a multiple choice question is worth ____ points.
Answers
Answer:
50-100-1-3
.......(?)
Answer:
I AM CONFUSION
Step-by-step explanation:
reduce into lowest terms
\( \frac{4}{6} \)
\( \frac{10}{12} \)
\( \frac{18}{24} \)
Answers
Answer:
4/6
We know that, 4 can be written as:
4 = 2 × 2 and 6 = 2 × 3.
In both 2 is common so cancel it out we get, 2/3
Similarly,
10/12
10 = 2 × 5 and 12 = 2 × 2 × 3
2 common and cancel we get, 5/6
18/24
18 = 2 × 3 × 3
24 = 2 × 2 × 2 × 3
6 (2 × 3) is common. So, cancel we get, 3/4
Find angle 1
PLS ANSWER ASAP

Answers
Answer:
80 degrees
Step-by-step explanation:
What we see in this drawing is a triangle formed by three lines. In order to solve this problem, we need to know that when two lines intersect, the two angles formed are supplementary (meaning they add up to 180 degrees). For example, the 150-degree angle, and the angle right next to it (the angle on the left side of the triangle) add up to 180 degrees. This means that the left-most angle of the triangle is 180-150, which is 30 degrees
We can figure out the topmost angle of the triangle using the same method. We know that the angle outside the triangle is 130 degrees, so the angle right next to it (in this case, right below it), is 180-130, or 50 degrees.
Next, we use the fact that triangles are 180 degrees on the inside to figure out the third angle (the one on the right, right next to angle 1). We know that the other two angles are 30 and 50 degrees, and if you add that up, you get 80 degrees. The last angle, then, is 180-80, or 100 degrees.
Lastly, we know that the rightmost angle of the triangle and angle 1 add up to 180 degrees. In other words, 100+Angle1=180. Therefore, Angle 1 is 180-100 or 80 degrees.
W(0,5), U(-2,1), V(2,1) of the triangle of scalene , isosceles, equilateral
Answers
The given vertices of the triangle of isosceles.
What is an isosceles triangle ??
An isosceles triangle in geometry is one with at least two sides that are of equal length. Both having exactly two sides of equal length and having at least two sides of equal length are acceptable specifications, with the latter version containing the equilateral triangle as an exception. The faces of bipyramids, the golden triangle, the isosceles right triangle, and some Catalan solids are all examples of isosceles triangles.
In this figure, it is an isosceles triangle as two sides of the triangle are equal.
The given vertices are W(0,5), U(-2,1) and V(2,1)
So the sides of the triangle is:
w =√ (2-(2))² + (1-1)² = √(4)² = 4
u =√ (2-0)² + (1-5)² = √(4 + 16) = 4√5
v = √ (-2-0)² + (1-5)² = √(4 + 16) = 4√5
So its have two side as equal length.
Hence, the triangle of isosceles.
Learn more about an isosceles triangle, by the following link
brainly.com/question/1475130
#SPJ1
Use a table and graph to show when her investment will be worth 10,000$

Answers
Solution
I think the interest is compounded yearly, if so
First, convert R as a percent to r as a decimal
r = R/100
r = 6.25/100
r = 0.0625 per year
A = 10000
P = 5000
\(A=P(1+\frac{r}{n})^{nt}\)\(\begin{gathered} 10000=5000(1+6.25)^t \\ \frac{10000}{5000}=(1+0.0625)^t \\ 2=(1.0625)^t \\ \ln 2=\ln (1.0625)^t \\ t=11.5 \end{gathered}\)Use logarithms or a scientific calculator
t = 11.5
In 11.5 years $5000 investment be worth of $10000
>>>>>>>>>>>>>
In case the interest is simple interest
Interest = Amount - Principal = $10000-$5000 = $5000
Time = 100*Interest / (Principal*Rate
= 100*5000 / (5000*6.25)
t = 16 years
In 16 years $5000 investment be worth of $10000
Please help me with this homework …

Answers
What are the solutions of this quadratic equation? x^2+13=8x+37
Answers
Answer:
\(x\in\left\{4-2\sqrt{10}\ ,\ \,4+2\sqrt{10}\,\right\}\)
Step-by-step explanation:
\(x^2+13=8x+37\\\\x^2-8x-24=0\\\\a=1\,,\ \ b=-8\,,\ \ c=-24\\\\x_1=\dfrac{-(-8)-\sqrt{(-8)^2-4\cdot1\cdot(-24)}}{2\cdot1}=\dfrac{8-\sqrt{64+96}}2=\dfrac{8-\sqrt{160}}2 =\\\\=\dfrac{8-4\sqrt{10}}2=\dfrac{2(4-2\sqrt{10})}2=4-2\sqrt{10} \\\\x_2=\dfrac{-(-8)-\sqrt{(-8)^2-4\cdot1\cdot(-24)}}{2\cdot1}=\dfrac{8+4\sqrt{10}}2=4+2\sqrt{10}\)
The solutions of the quadratic equation x² + 13 = 8x + 37 are x = 4 + 2√10 and x = 4 - 2√10.
What is a quadratic equation?The quadratic equation is defined as a function containing the highest power of a variable is two.
The given equation as:
x² - 8x + 13 = 37
Subtracting 37 from both sides, we get:
x² - 8x - 24 = 0
Now, we have the equation in standard form, so we can use the quadratic formula to find the solutions:
x = (-b ± √(b² - 4ac)) / 2a
Here, a = 1, b = -8, and c = -24.
Substitute these values into the quadratic formula, and we get:
x = (-(-8) ± √((-8)² - 4(1)(-24))) / 2(1)
x = (8 ± √(64 + 96)) / 2
x = (8 ± √160) / 2
x = (8 ± 4√10) / 2
Simplifying, we get:
x = 4 ± 2√10
Therefore, the solutions of the quadratic equation x² + 13 = 8x + 37 are x = 4 + 2√10 and x = 4 - 2√10.
Learn more about quadratic function here:
brainly.com/question/14083225
#SPJ3
What is 4000*800I need help math
Answers
Answer:
3200000
Step-by-step explanation:
4000*800 is 3200000
write these products as sums: a.sin(3x)cos(2x)
b.cos(7x)cos(2x)
Answers
Answer:
Step-by-step explanation:
a. To write the product a.sin(3x)cos(2x) as a sum, we can use the identity:
sin(a+b) = sin(a)cos(b) + cos(a)sin(b)
Using this identity, we can write:
a.sin(3x)cos(2x) = a.sin(3x)cos(x + x)
= a[sin(3x)cos(x) + cos(3x)sin(x)]
= a[sin(x)cos(3x) + sin(3x)cos(x)]
= a.sin(x)(cos(3x) + sin(3x))
Therefore, the product a.sin(3x)cos(2x) can be written as the sum a.sin(x)(cos(3x) + sin(3x)).
b. To write the product cos(7x)cos(2x) as a sum, we can use the identity:
cos(a+b) = cos(a)cos(b) - sin(a)sin(b)
Using this identity, we can write:
cos(7x)cos(2x) = cos(7x)cos(-x - (-x + 2x))
= cos(7x)cos(-x)cos(-(-x+2x)) - sin(7x)sin(-x)cos(-(-x+2x))
= cos(7x)cos(x)cos(x) + sin(7x)sin(x)sin(x)
= cos(7x)cos^2(x) + sin(7x)sin^2(x)
Therefore, the product cos(7x)cos(2x) can be written as the sum cos(7x)cos^2(x) + sin(7x)sin^2(x).
A person standing at the edge of a cliff 48 feet tall throws a ball up and just off the cliff with an initial upward velocity of 8 feet per second. What is the maximum height of the ball? When will the ball hit the ground?
The ball will be at its highest at ___
feet.
The ball will hit the ground at t =___
second(s)
Answers
Check the picture below.
since the cliff is 48 feet tall, thus that its initial height.
\(~~~~~~\textit{initial velocity in feet} \\\\ h(t) = -16t^2+v_ot+h_o \quad \begin{cases} v_o=\textit{initial velocity}&8\\ \qquad \textit{of the object}\\ h_o=\textit{initial height}&48\\ \qquad \textit{of the object}\\ h=\textit{object's height}&\\ \qquad \textit{at "t" seconds} \end{cases} \\\\\\ h(t)=-16t^2+8t+48\)
well, as you can see in the picture, its maximum is at its vertex, so
\(\textit{vertex of a vertical parabola, using coefficients} \\\\ y=\stackrel{\stackrel{a}{\downarrow }}{-16}x^2\stackrel{\stackrel{b}{\downarrow }}{+8}x\stackrel{\stackrel{c}{\downarrow }}{+48} \qquad \qquad \left(-\cfrac{ b}{2 a}~~~~ ,~~~~ c-\cfrac{ b^2}{4 a}\right) \\\\\\ \left(-\cfrac{ 8}{2(-16)}~~~~ ,~~~~ 48-\cfrac{ (8)^2}{4(-16)}\right)\implies \left(\cfrac{1}{4}~~,~~48-\cfrac{64}{-64} \right)\)
\(\left( \frac{1}{4}~~,~~48+1 \right)\implies \stackrel{\textit{the ball is at highest}}{\left(\frac{1}{4}~~,~~\stackrel{\downarrow }{49} \right)}\)
well, it hits the ground when y = 0.
\(\stackrel{h(t)}{0}=-16t^2+8t+48\implies 0=8(-2t^2+t+6)\implies 2t^2-t-6=0 \\\\\\ (2t+3)(t-2)=0\implies t= \begin{cases} -\frac{3}{2}\\\\ 2~~\textit{\large \checkmark} \end{cases}\)
notice, we didn't use the negative value, since "t" must be greater than 0.

Solve the equation. -1 + x = -10 x =
Answers
Answer:
-1
Step-by-step explanation:
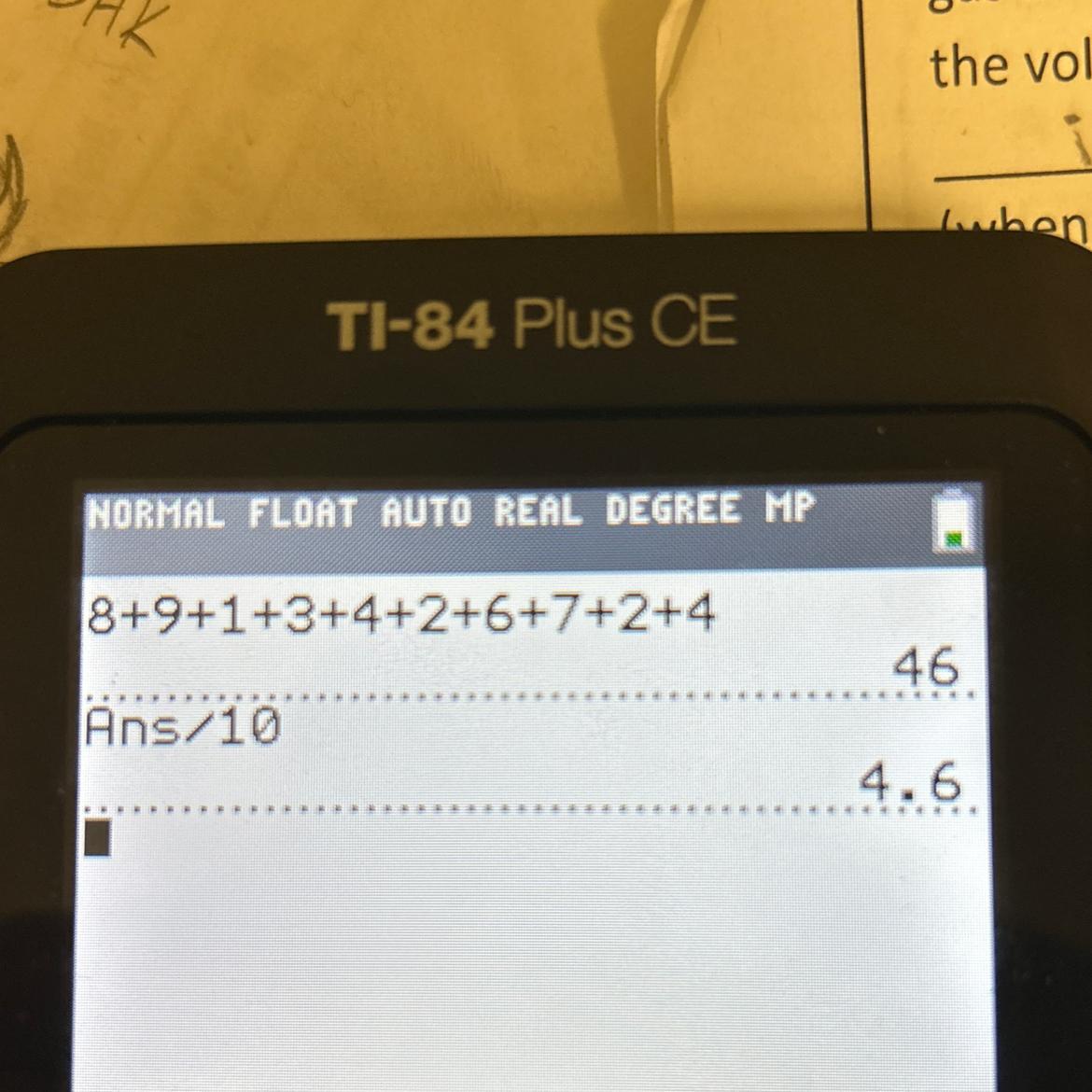
1) Find the average of the numbers:
8, 9, 1, 3, 4, 2, 6, 7, 2, 4
Answers
Could be wrong but pretty sure you add all the numbers then divide the total by the amount of numbers you just added
What is the value of the expression below when z=5 and w=5
9z-3w
Answers
Answer:
you should get 30 as an answer
Step-by-step explanation:
9*5=45
3*5=15
45-15=30
G(Q) = 5 + 3Q + 202 - Q2 C2(Q) = 3 + 4Q + 2 1. Find the MC function for both C1(Q) AND C2(Q). 2. Find AVC function for both Ci(Q) AND C2(Q). 3. Find AFC function for both C1(Q) AND C2(Q). 4. Find AC function for both Ci(Q) AND C2(Q). 5. Find ATC function for both Ci(Q) AND C2(Q).
Answers
For C1(Q) = 3 - 2Q.
For C2(Q) = 4.
2. The AVC function
For C1(Q) = 5/Q + 3 + 20/Q - Q.
For C2(Q) = 3/Q + 4 + 2/Q.
3. The AFC function
For C1(Q)= 5/Q - 20/(5 + 3Q + 20/Q - Q)
For C2(Q) = 0.
4. To find the AC function
For C1(Q) = (5 + 3Q + 202 - Q^2)/Q + 5/Q - 20/(5 + 3Q + 20/Q - Q).
For C2(Q) = (3 + 4Q + 2)/Q + 3/Q + 4 + 2/Q.
5.To find the ATC function
For C1(Q)= 5/Q² + 3/Q + 20/Q² - Q/Q + 5/Q - 20/(5Q + 3Q² + 20 - Q²)
For C2(Q)= 3/Q² + 4/Q + 2/Q² + 3/Q + 4/Q + 2/Q.
Find the ATC functions for C1(Q) and C2(Q) given the provided cost functions?
1. To find the MC function, we take the derivative of the cost functions with respect to Q.
For C1(Q) = 5 + 3Q + 202 - Q^2, MC1(Q) = 3 - 2Q.
For C2(Q) = 3 + 4Q + 2, MC2(Q) = 4.
2. To find the AVC function, we divide the cost functions by Q.
For C1(Q), AVC1(Q) = (5 + 3Q + 202 - Q^2)/Q = 5/Q + 3 + 20/Q - Q.
For C2(Q), AVC2(Q) = (3 + 4Q + 2)/Q = 3/Q + 4 + 2/Q.
3. To find the AFC function, we subtract the AVC function from the ATC function.
For C1(Q), AFC1(Q) = (5 + 3Q + 202 - Q^2)/Q - (5 + 3Q + 202 - Q^2)/(5 + 3Q + 20/Q - Q)
= 5/Q - 20/(5 + 3Q + 20/Q - Q).
For
C2(Q), AFC2(Q) = (3 + 4Q + 2)/Q - (3 + 4Q + 2)/(3/Q + 4 + 2/Q) = 0.
4. To find the AC function, we add the AVC function to the AFC function.
For
C1(Q), AC1(Q) = (5 + 3Q + 202 - Q^2)/Q + 5/Q - 20/(5 + 3Q + 20/Q - Q).
For
C2(Q), AC2(Q) = (3 + 4Q + 2)/Q + 3/Q + 4 + 2/Q.
5. To find the ATC function, we divide the AC function by Q.
For
C1(Q), ATC1(Q) = [(5 + 3Q + 202 - Q²)/Q + 5/Q - 20/(5 + 3Q + 20/Q - Q)]/Q
= 5/Q² + 3/Q + 20/Q² - Q/Q + 5/Q - 20/(5Q + 3Q² + 20 - Q²).
For
C2(Q), ATC2(Q) = [(3 + 4Q + 2)/Q + 3/Q + 4 + 2/Q]/Q
= 3/Q² + 4/Q + 2/Q² + 3/Q + 4/Q + 2/Q.
Learn more about Average Total Cost
brainly.com/question/29306232
#SPJ11
Find the area of the figure.
area
units2

Answers
Answer:
\(33 units^{2}\)
I counted the squares.
what type of angle is x??
