Answers
Answer:
42°
Step-by-step explanation:
its 42° because its smaller than 48° and that's the only option smaller lol
Answer:
42 degrees
Step-by-step explanation:
The angle forms a right angle, which in total would be 90 degrees.
48 + 42 would be the only option because it is the only one that adds up to 90 degrees.
Related Questions
Seth earns $25 a day and $3 for each ticket he sells at the local theatre. Write and solve annequality that can be used to find how many tickets he must sell in a day to earn at least $115Write an inequality. *
Answers
Let x represent the number of tickets that he sold at the local theatre.
From the information given, Seth earns $25 a day and $3 for each ticket he sells at the local theatre. The expression representing the amount earned from selling x tickets in a day is
25 + 3x.
To earn at least $115, it means that the amount he would earn is greater than or equal to $115. the symbol for 'greater than or equal to' is '≥'
Therefore, the inequality representing this scenario is
25 + 3x ≥ 115
To solve the inequality, we would subtract 25 from both sides of the inequality. We have
25 - 25 + 3x ≥ 115 - 25
3x ≥ 90
Dividing both sides of the inequality by 3, we have
3x/3 ≥ 90/3
x ≥ 30
He must sell at least 30 tickets to earn at least $115
IF A KIND SOUL WILL HELP ME I WOULD BE SO GRATEFUL!!!!!!!!!!!
Which of the following statements must be true about parallelogram ABCD?

Answers
B
Explanation:
I think it is B because the sides AD and BC are opposite to each other making the parallel
Hence , write down the equation with y as the subject ( in terms of x ). The value of m and q must be indicated
Answers
The equation with y as the subject is y = x^m / (4x^n - 2)
To solve for y as the subject of the equation, we need to isolate y on one side of the equation. Here's how we can do it,
First, we can rearrange the equation to get all the y terms on one side:
4x^n y - 2y = x^m
Next, we can factor out y from the left-hand side,
y(4x^n - 2) = x^m
Finally, we can divide both sides by (4x^n - 2) to isolate y,
y = x^m / (4x^n - 2)
Therefore, the equation with y as the subject is:
y = x^m / (4x^n - 2)
where m and n are the constants given in the original equation.
Learn more about equation here
brainly.com/question/28724345
#SPJ4
The given question is incomplete, the complete question is:
Hence , write down the equation with y as the subject ( in terms of x ). The value of m and q must be indicated. equation 4x^ny -2y - x^m = 0, m and n are constant
Sketch the curve represented by the parametric equations (indicate the orientation of the curve), and write the corresponding rectangular equation by eliminating the parameter. X = 4t − 3, y = 3t 1
Answers
The parametric equation in the form of x and y will be y = 3x/4 + 13/4. And the graph is shown below.
What is a parametric equation?Or any one of a system of parameters either express equal positions of the vertices of curvature as derivatives of one factor or reflects the positions of the locations of a plane as variables of two factors is known as a parametric equation.
The parametric equation is given below.
x = 4t − 3 and y = 3t + 1
Then
x = 4t − 3
t = (x + 3)/4
Put the value of t in equation y = 3t + 1, then we have
y = 3(x + 3)/4 + 1
y = 3x/4 + 9/4 + 1
y = 3x/4 + 13/4
Then the graph of the equation is given below.
More about the parametric equation link is given below.
https://brainly.com/question/9056657
#SPJ4

Let F(x, y) = (9x + 5y)i + (2x – 7y?)j. Let D be the rectangle {(x, y)|0 < x < 2,0 Sy < 1} and let C be the boundary of D, oriented counterclockwise. (a) (4 points) Use Green's Theorem to compute the circulation f F. dr. Your solution should involve a double integral. (b) (2 points) Is F equal to V f for some function f? Use your work from part (a) to justify your answer. (c) (4 points) Use Green's Theorem to compute the flux f(F. n)ds where n denotes the outward-pointing unit normal vector. Your solution should involve a double integral. (d) (2 points) Is F equal to V x G for some vector field G? Use your work from part (C) to justify your answer.
Answers
The circulation of F around C is -16. No, F is not equal to V f for some function f. The flux of F across C is -8. No, F is not equal to V x G for any vector field G.
(a) The circulation of F around C is -16.
Using Green's Theorem, we can write the circulation of F as the line integral around the boundary of D:
∮CF · dr = ∬D (∂Q/∂x - ∂P/∂y) dA
where P = 9x + 5y, Q = 2x - 7y, and dr = dx i + dy j.
Taking the partial derivatives, we get:
∂Q/∂x - ∂P/∂y = 2 - 9 = -7.
Thus, the circulation of F around C is:
∮CF · dr = ∬D -7 dA = -7(area of D) = -16.
(b) No, F is not equal to V f for some function f.
If F were equal to the gradient of some scalar function f, then the circulation of F around any closed path would be zero. However, we just calculated that the circulation of F around C is -16, which means F cannot be expressed as the gradient of any scalar function.
(c) The flux of F across C is -8.
Using Green's Theorem, we can write the flux of F across C as the line integral around the boundary of D:
∮CF · ds = ∬D (∂P/∂x + ∂Q/∂y) dA
Taking the partial derivatives, we get:
∂P/∂x + ∂Q/∂y = 9 - 7 = 2.
Thus, the flux of F across C is:
∮CF · ds = ∬D 2 dA = 2(area of D) = -8.
(d) No, F is not equal to V x G for any vector field G.
If F were equal to the curl of some vector field G, then the flux of F across any closed surface would be zero. However, we just calculated that the flux of F across C is -8, which means F cannot be expressed as the curl of any vector field.
Learn more about flux here
https://brainly.com/question/26289097
#SPJ11
Help Me Please I need help

Answers
Answer:
Step-by-step explanation:
m = \(\frac{y_{2} -y_{1} }{x_{2} -x_{1} }\)
y - \(y_{1}\) = m( x - \(x_{1}\) )
y = mx + b
~~~~~~~~~~~
(4, 5)
( - 6, 15)
m = (15 - 5) / ( - 6 - 4 ) = - 1
y - 5 = ( - 1)( x - 4 )
y = (- 1) x + 9
Manuel the trainer has two solo workout plans that he offers his clients: plan a and plan b. each client does either one or the other (not both). on monday there were 3 clients who did plan a and 8 who did plan b. manuel trained his monday clients for a total of 7 hours and his tuesday clients for a total of 6 hours. how long does each workout plans last?
Answers
Plan a lasts 1/5 of an hour (or 12 minutes) and plan b lasts 29/5 hours (or 5 hours and 48 minutes).
Let's denote the length of plan a by 'a' and the length of plan b by 'b' (measured in hours).
From the problem, we know that:
- On Monday, 3 clients did plan a and 8 clients did plan b. Therefore, the total time spent on plan a on Monday was 3a and the total time spent on plan b on Monday was 8b.
- On Tuesday, we don't know how many clients did each plan, but we do know that the total time spent on both plans was 6 hours.
Putting these together, we can create a system of two equations:
3a + 8b = 7 (total time spent on Monday)
a + b = 6 (total time spent on Tuesday)
We can solve this system by using substitution. Rearranging the second equation, we get:
b = 6 - a
Substituting this expression for b into the first equation, we get:
3a + 8(6 - a) = 7
Simplifying and solving for a, we get: a = 1/5
Substituting this value back into the expression for b, we get:
b = 6 - a = 29/5
To know more about equations refer to
https://brainly.com/question/29174899
#SPJ11
Which is the graph of y-3 =-2/3(x+6)?
plz help

Answers
Answer:
I belive the answer is the first graph.
Step-by-step explanation:
When solving the equation as a function, the answer is -3/2.
0-3 = -2/3x - 4
-3 = -2/3x - 4
-9 = -2x - 12
2x = -12 + 9
2x = -3
Divide for: x = -3/2
What is the minimum of the sinusoidal function?
Enter your answer in the box.
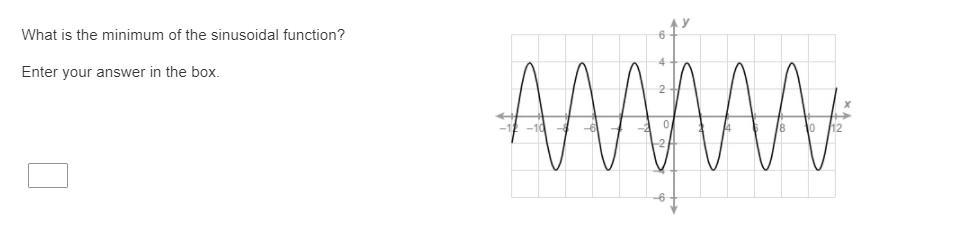
Answers
Answer:
The minimum is y=-5. The max would be y=1
Step-by-step explanation:
because y=5 and the max would be y=1
Answer:
its -4
Step-by-step explanation:
i took the test :)
1. Write an exponential function to represent the spread of Ben's social media post.
2. Write an exponential function to represent the spread of Carter's social media post.
3. Graph each function using at least three points for each curve. All graphs should be placed together on the
same coordinate plane, so be sure to label each curve. You may graph your equation by hand on a piece of
paper and scan your work, or you may use graphing technology.
Answers
1. An exponential function to represent the spread of Ben's social media post is \(f(x) = 2(3)^x\)
2. An exponential function to represent the spread of Carter's social media post is \(f(x) = 10(2)^x\)
3. A graph of each function with three points for each curve is shown below.
How to write an exponential function to represent the spread?In Mathematics and Geometry, an exponential function can be modeled by using this mathematical equation:
\(f(x) = a(b)^x\)
Where:
a represents the initial value or y-intercept.x represents x-variable.b represents the rate of change or common ratio.Based on the table of values, the initial value is 2. Next, we would determine the common ratio (b) as follows;
Common ratio, b = a₂/a₁
Common ratio, b = 6/2 = 3.
Therefore, the required exponential function is given by;
\(f(x) = 2(3)^x\)
Part 2.
For Carter's social media post, we have the following exponential function:
\(f(x) = a(b)^x\\\\f(x) = 10(2)^x\)
Part 3.
In this scenario and exercise, we would use an online graphing calculator to plot the above exponential functions as shown in the graph attached below.
Read more on exponential equation here: brainly.com/question/28939171
#SPJ1


In a large population, 60% of all adults wear glasses. Assume that 10 adults are independently selected from this population. Answer the following by showing all the work and rounding your answers to three decimals.
(a) What is the probability that one of the selected adults wears glasses?
(b) What is the expected number of adults not wearing glasses in this selection?
(c) Find the probability that more than three but no more than five of the selected adults will not be wearing glasses.
(d) What is the standard deviation of the number of adults not wearing glasses in this selection?
Answers
a. The probability that one of the selected adults wears glasses is 0.323.
b. The expected number of adults not wearing glasses in this selection is 4.
c. The probability that more than three but no more than five of the selected adults will not be wearing glasses is 0.451.
d. The standard deviation of the number of adults not wearing glasses in this selection is 1.385.
(a) To find the probability that one of the selected adults wears glasses, we can use the binomial distribution formula:
P(X = k) = \({}^nC_k\) × \(p^k\) × \((1-p)^{(n-k)}\)
where n is the number of trials (in this case, 10), k is the number of successes (in this case, 1), p is the probability of success (in this case, 0.6), and (1-p) is the probability of failure (in this case, 0.4).
Substituting these values, we get:
P(X = 1) = \({}^nC_k\) × \(0.6^1\) × \(0.4^9\)
= 10 × \(0.6^1\) × \(0.4^9\)
= 0.323
So the probability that one of the selected adults wears glasses is 0.323.
(b) To find the expected number of adults not wearing glasses, we can use the formula:
E(X) = n × (1 - p)
where n is the number of trials (in this case, 10) and p is the probability of success (in this case, 0.6).
Substituting these values, we get:
E(X) = 10 × (1 - 0.6)
= 4
So the expected number of adults not wearing glasses is 4.
(c) To find the probability that more than three but no more than five of the selected adults will not be wearing glasses, we can use the binomial distribution formula again:
P(3 < X < 6) = P(X = 4) + P(X = 5)
Substituting the values using the formula, we get:
P(X = 4) = 10 choose 4 × \(0.4^4\) × \(0.6^6\)
= 210 × \(0.4^4\) × \(0.6^6\)
= 0.250
P(X = 5) = 10 choose 5 × \(0.4^5\) × \(0.6^5\)
= 252 × \(0.4^5\) × \(0.6^5\)
= 0.201
Therefore,
P(3 < X < 6) = P(X = 4) + P(X = 5)
= 0.250 + 0.201
= 0.451
So the probability that more than three but no more than five of the selected adults will not be wearing glasses is 0.451.
(d) To find the standard deviation of the number of adults not wearing glasses, we can use the formula:
SD(X) = √(n × p × (1 - p))
Substituting the values, we get:
SD(X) = √(10 × 0.6 × 0.4)
= 1.385
So the standard deviation of the number of adults not wearing glasses is 1.385.
Learn more about the probability at
https://brainly.com/question/30034780
#SPJ4
Let P(n) be the statement that 13 + 23+….n3 = (n(n + 1) / 2)² for the positiveinteger n. a.) What is the statement P(1)? b.) Showthat P(1), completing the basis step of theproof?
Answers
Since both sides of the equation are equal, we have completed the basic step of the proof, showing that P(1) is true.
a.) The statement P(1) is obtained by substituting n=1 into the equation. So, P(1) would be: 1³ = (1(1 + 1) / 2)²
b.) To show that P(1) is true, we need to prove that both sides of the equation are equal:
Left side: 1³ = 1
Right side: (1(1 + 1) / 2)² = (1(2) / 2)² = (2 / 2)² = 1² = 1
Since both sides of the equation are equal, we have completed the basic step of the proof, showing that P(1) is true.
learn more about the statement
https://brainly.com/question/10705953
#SPJ11
a) The equation is not true for n = 1, so P(1) is false.
b) The positive integer n, 13 + 23 + … + n3 = (n(n + 1) / 2)²" is not true for n = 1
a) To find P(1), we substitute n = 1 into the equation given:
13 = (1(1 + 1) / 2)²
13 = (1 / 2)²
13 = 1/4
The equation is not true for n = 1, so P(1) is false.
b) To complete the basic step of the proof, we need to show that P(1) is true.
However, we have just shown that P(1) is false.
This means that the statement "for the positive integer n, 13 + 23 + … + n3 = (n(n + 1) / 2)²" is not true for n = 1.
Therefore, the proof cannot proceed and is incomplete.
for such more question on integer
https://brainly.com/question/929808
#SPJ11
A) Consider the functions f(x)=x+1 and g(x)=3^x―2 solve f(x)= g(x)
B) Write down the interval for the values of for which F(X)>G(X)
Answers
Answer:
AEFsdgfdhzfddf
Step-by-step explanation:
6. How many real-number solutions does the equation have?
0=3x62+18x+27
a. one solution
b. two solutions
c. no solutions
d. infinitely many solutions
I think it's A but I'm not too sure...
Answers
Answer:
well for starters
the answer you get when you factor it out is 3(x+3)(x+3)
i know that would mean x=-3 but i dont know how the big 3 would effect anything. hope this helps
T/F : If the first and second rows of an augmented matrix are (1,1,0) and (0,1,0) respectively, then the matrix is not in reduced row echelon form.
Answers
False.
the given augmented matrix is in reduced row echelon form.
The augmented matrix is said to be in reduced row echelon form (RREF) if it satisfies the following conditions:
1. The first nonzero element in each row (called the "pivot") is 1.
2. The pivot in each row is to the right of the pivot in the previous row.
3. All entries above and below each pivot are zero.
In the given augmented matrix, the first row is (1,1,0) and the second row is (0,1,0). Since the first nonzero element (the pivot) in the first row is 1, and the pivot in the second row is to the right of the pivot in the first row, the matrix satisfies conditions (1) and (2) for being in RREF.
Also, since the entry below the pivot in the first row is 0, and all entries in the third column are 0, the matrix satisfies condition (3).
Therefore, the given augmented matrix is in reduced row echelon form.
Visit to know more about Matrix:-
brainly.com/question/2456804
#SPJ11
Find the square root.

Answers
A researcher wants to set up a regression equation where Y is a function X. Evaluate the researcher’s options given the following scenarios: (3)
i. Y is I(0); X is I(0)
ii. Y is I(2); X is I(0)
iii. Y is I(1); X is I(1); and the error term is I(0).
Answers
The appropriate regression model depends on the stationarity properties of both the dependent and independent variables, as well as the error term. The researcher can use a standard OLS regression model with first-order differencing of both Y and X.
In the first scenario, both Y and X are I(0), which means they are stationary time series. In this case, the researcher can perform a standard linear regression analysis, as the stationary series would lead to a stable long-run relationship. The answer from this model will be reliable and less likely to suffer from spurious regressions. In the second scenario, Y is I(2) and X is I(0). This implies that Y is integrated of order 2 and X is stationary. In this case, the researcher should first difference Y twice to make it stationary before performing a regression analysis. However, this approach might not be ideal as the integration orders differ, which can lead to biased results.
In the third scenario, Y and X are both I(1) and the error term is I(0). This indicates that both Y and X are non-stationary time series, but their combination might be stationary. The researcher should employ a co-integration analysis, such as the Engle-Granger method or Johansen test, to identify if there is a stable long-run relationship between Y and X. If co-integration is found, then an error correction model can be used for more accurate predictions.
To know more about regression visit:-
https://brainly.com/question/28168620
#SPJ11
Find the limits of the following sequences. You should show your working, but standard results from the course can be used without comment. en e (a) (5²+1+7²3). and (b) ( (n+1)(n −n+1) (3n³ + 2n + 1) (n — 5) +n³ nEN [6 marks] nEN
Answers
The limit of the sequence in part (a), given by (5²+1+7²3), is equal to 125. The limit of the sequence in part (b), given by ((n+1)(n −n+1)(3n³ + 2n + 1)(n — 5) +n³), as n approaches infinity, is also equal to 125.
(a) To find the limit of the sequence (5²+1+7²3) as n approaches infinity, we simplify the expression. The term 5²+1 simplifies to 26, and 7²3 simplifies to 22. Therefore, the sequence can be written as 26 + 22, which equals 48. Since this is a constant value independent of n, the limit of the sequence is equal to 48.
(b) To find the limit of the sequence ((n+1)(n −n+1)(3n³ + 2n + 1)(n — 5) +n³) as n approaches infinity, we simplify the expression. We expand the expression to get (n³ + n²)(3n³ + 2n + 1)(n — 5) + n³. Multiplying these terms together, we get (3n⁷ + 8n⁶ - 19n⁵ - 51n⁴ - 51n³ + 26n² + 5n). As n approaches infinity, the highest degree term dominates the sequence. Therefore, the limit of the sequence is equal to 3n⁷. Substituting n with infinity gives us infinity to the power of 7, which is also infinity. Hence, the limit of the sequence is equal to infinity.
Learn more about sequence here:
https://brainly.com/question/19819125
#SPJ11
the graph above represents position x versus time t for an object being acted on by a constant force. the average speed during the interval between 1 s and 2 s is most nearly]
(A) 2 m/s (B) 4 m/s (C) 5 m/s (D) 6 m/s (E) 8 m/s
Answers
The average speed during the interval between 1 second and 2 seconds is most nearly 8 m/s, which corresponds to option (E).
To determine the average speed during the interval between 1 second and 2 seconds, we need to find the displacement of the object during that time interval and divide it by the duration.
Looking at the graph, we can observe that the object's position increases from approximately 0 meters at 1 second to approximately 8 meters at 2 seconds.
Therefore, the displacement is 8 meters - 0 meters = 8 meters.
The duration of the time interval is 2 seconds - 1 second = 1 second.
To calculate the average speed, we divide the displacement by the duration:
Average speed = Displacement / Duration = 8 meters / 1 second = 8 m/s.
Therefore, the average speed during the interval between 1 second and 2 seconds is most nearly 8 m/s, which corresponds to option (E).
To know more about Average speed refer here:
https://brainly.com/question/10449029#
#SPJ11
In right triangle ABC, m B Em C. Let sin B = r and cos B = s.
B
А
С
Which expression represents the value of sin C - cos C?
rts
71
S
S-
S
Answers
The expression that represents the value of sin C - cos C is s-r
From the triangle ABC, since sin B = r and cos B = s.=, hence;
Opposite side= rAdjacent side = sHypotenuse = 1If m<C is the reference angle, then;
Opposite side= s
Adjacent side = r
Hypotenuse = 1
Sin C = s and cos C = r
Hence the expression that represents the value of sin C - cos C is s-r
Learn more on trigonometry here: https://brainly.com/question/20519838
Solve the system of equations by substitution. x + y=7 y=6x The solution of the system is?
Answers
Answer:
The solution to the system is (1, 6)
Step-by-step explanation:
Trust me its correct
pls mark me as brainliest
what is y???
thanks for helping

Answers
\(y=35+25=\bf60\)
Answer:
60
Step-by-step explanation:
find x first
180 - 35 - 25 = 120
x = 120
so y = 180-120
total angles in a triangle is 180
straight line also 180
please help me solve it.

Answers
\(\dfrac{n^6}{(n^2)^5}\\\\\\=\dfrac{n^6}{n^{2 \times 5}}\\\\\\=\dfrac{n^6}{n^{10}}\\\\\\=n^{6-10}\\\\\\=n^{-4}\)
suppose point P(4,-9) is transmitted according to rule (x,y)→(x+3,y-2),what are the coordinates of P
Answers
Answer:
p(7,-11)
that is the answer of the coordinates
Which are the solutions for the inequality m > - 9?
Answers
approximately how many acres are there in a lot 1 2 mile by 1 2 mile
Answers
1 mile is equal to 640 acres. Therefore, a lot that is 1/2 mile by 1/2 mile is approximately equal to 160 acres.
To determine the number of acres in a lot that is 1/2 mile by 1/2 mile, we need to convert the measurements to the same unit and then use the conversion factor for acres.
1 mile is equal to 640 acres. Therefore, we can calculate the area in square miles first.
Area = Length x Width = (1/2 mile) x (1/2 mile) = 1/4 square mile
To convert square miles to acres, we multiply by the conversion factor of 640 acres per square mile:
Area in acres = (1/4 square mile) x (640 acres/square mile) = 160 acres
Therefore, a lot that is 1/2 mile by 1/2 mile is approximately equal to 160 acres.
Learn more about mile here:
https://brainly.com/question/16151549
#SPJ11
Using a stopwatch, Tyrone determines it takes him 58.2 minutes to travel 30 miles to work. The stopwatch measures to hundredths of a minute. Going by the accuracy of the stopwatch, which is the most accurate determination for the number of feet per second Tyrone traveled on his way to work? 1 mile = 5,280 feet 19.8 feet per second 19.84 feet per second 45.3 feet per second 45.36 feet per second
Answers
Answer:45.36 FEET PER SECOND GET IT IG
Step-by-step explanation:
The most accurate determination for the number of feet per second Tyrone traveled on his way to work is D. 45.36 feet per second
Calculations and ParametersGiven the parameters:
time= 58.2 minutes
distance= 30 miles
Therefore, we would convert and solve:
(30*5280)/58.2*60
=158400/582*6
=158400/3492
=45.36per sec
Read more about distance and time here:
https://brainly.com/question/2854969
#SPJ9
where did Goku die nnnnnnnnnnnnnnnnnnnnnnnn
Answers
Answer:
Goku died you I just started watching
What is the equation of the following line written in general form? (The y-intercept is -1.)

Answers
Answer:
2x-y-1=0
Step-by-step explanation:
.
Consider the matrix that transforms a vector (x1, x2, x3) into (x2, x3, x1) in 3D:
1-Show that this is a rotation matrix.
2-Find the axis of rotation.
3-Find the angle of rotation
Answers
1- This is a rotation matrix because the determinant is 1 and the transpose is equal to the inverse. 2- The line passing through the origin and the point (1, 1, 1) is the axis of rotation. 3- 120° is the angle of rotation.
1. To show that this is a rotation matrix, we need to check that the matrix satisfies the following properties:
- The determinant of the matrix is 1.
- The transpose of the matrix is equal to its inverse.
The matrix that transforms a vector (x1, x2, x3) into (x2, x3, x1) is:
| 0 1 0 |
| 0 0 1 |
| 1 0 0 |
The determinant of this matrix is:
det = 0×0×0 + 1×1×1 + 0×0×0 - 0×0×1 - 1×0×0 - 0×1×0 = 1
The transpose of this matrix is:
| 0 0 1 |
| 1 0 0 |
| 0 1 0 |
The inverse of this matrix is:
| 0 0 1 |
| 1 0 0 |
| 0 1 0 |
Since the determinant is 1 and the transpose is equal to the inverse, this is a rotation matrix.
2. To find the axis of rotation, we need to find the eigenvector of the matrix corresponding to the eigenvalue of 1. The characteristic equation of the matrix is:
| -λ 1 0 |
| 0 -λ 1 |
| 1 0 -λ | = 0
Expanding the determinant, we get:
-λ × (-λ × (-λ)) - 1 × 1 x 1 = 0
λ = 1
The eigenvector corresponding to the eigenvalue of 1 is:
| -1 1 0 | | x1 | = | 0 |
| 0 -1 1 | | x2 | | 0 |
| 1 0 -1 | | x3 | | 0 |
Solving this system of equations, we get:
x1 = x2 = x3
So the eigenvector is:
| 1 |
| 1 |
| 1 |
This means that the axis of rotation is the line passing through the origin and the point (1, 1, 1).
3. To find the angle of rotation, we can use the formula:
cosθ = (trA - 1)/2
Where trA is the trace of the matrix A. The trace of the matrix is:
trA = 0 + 0 + 0 = 0
So the angle of rotation is:
cosθ = (0 - 1)/2 = -1/2
θ = 120°
Therefore, the angle of rotation is 120°.
You can learn more about matrix at: brainly.com/question/28180105
#SPJ11
