Solve the system of equations using matrices. Use the Gaussian elimination method with back-substitution.
x+y-z=-3
4x-y+z=8
-x+5y-4z=1
The solution set is ?
Answers
Answer:
Step-by-step explanation:
Ⅰ. x+y-z = -3
Ⅱ. 4x-y+z = 8
Ⅲ. -x+5y-4z = 1
Use equation Ⅰ to eliminate the x terms from equations Ⅱ and Ⅲ.
Ⅰ. x+y-z = -3
Ⅱ. -5y+5z = 20
Ⅲ. 6y-5z = -2
Divide equation Ⅱ by the coefficient of its y term:
Ⅰ. x+y-z = -3
Ⅱ. y-z = -4
Ⅲ. 6y-5z = -2
Use equation Ⅱ to eliminate the y terms from equation Ⅲ.
Ⅰ. x+y-z = -3
Ⅱ. y-z = -4
Ⅲ. z = 22
Divide equation Ⅲ by the coefficient of its z term:
Ⅰ. x+y-z = -3
Ⅱ. y-z = -4
Ⅲ. z = 22
Back-substitution
y = -4 - (-1)z = 18
x = -3 - (1)y - (-1)z = 1
Related Questions
you can have the points
Answers
what two numbers multiply to -36 and add to -5
Answers
Answer:
9 and -4 is the answer it should be correct
Tim saw that a pair of $200 dollar jeans had been marked down by 20%. He told his friend that if you took the new price of the jeans and increased that value by 20%, the jeans would return to the original price of $200. is he correct or no?
Answers
Hey there!
The answer is no, they would not return to the original price of $200.
This is because when you decrease 200 by 20%, you get 160. Then, if you increase 160 by 20%, you get 192. This is because 20% of 200 and 20% of 160 is different.
Hope this helps! Have a great day, and good luck on your assignment!
Can someone answer my past questions thanks
Answers
Response:
I'll try if I can but
BRAINLIEST? Thanks!Lily has 4 cups of apples, 5-½ cups of watermelon, and cups of
grapes. She needs 2½ times of each fruit to make her fruit bowl. How
much of each fruit does she need? Do not round. Write your answer as
a whole number or as a mixed number. Use "/" as a fraction bar. Do
not label your answers.
a. Apples
b. Watermelons
c. Grapes

Answers
a. Apples: Lily needs 10 cups of apples for her fruit bowl.
b. Watermelons: Lily needs 13-3/4 cups of watermelons for her fruit bowl.
c. Grapes: The amount of grapes that Lily has is not given
What is arithmetic sequence?
An arithmetic sequence is a sequence of numbers in which each term after the first is found by adding a fixed constant number, called the common difference, to the preceding term.
To make her fruit bowl, Lily needs 2½ times the amount of each fruit she currently has.
a. Apples:
2½ × 4 cups = 10 cups
Therefore, Lily needs 10 cups of apples for her fruit bowl.
b. Watermelons:
2½ × 5-½ cups = (2 × 5 + 1/2) × 5/2 cups = 13-3/4 cups
Therefore, Lily needs 13-3/4 cups of watermelons for her fruit bowl.
c. Grapes:
The amount of grapes that Lily has is not given, so we cannot calculate how much she needs for her fruit bowl.
To learn more about arithmetic sequence from the given link:
https://brainly.com/question/15412619
#SPJ1
a technology company is studying the launch of their new laptop computers in order to track warranty purchases. assume that the laptop warranties have an unknown distribution with a mean of 243 days and a standard deviation of 34 days. a sample of 40 laptop warranty purchases are randomly selected from the population.use a calculator to find the probability that the average laptop warranty purchase for the sample will be greater than 253. round your answers to three decimal places.provide your answer below:
1. Drag and move the blue dot to select the appropriate probability graph area from the four options on the left. (Note- there are four graphs available to choose from. Only select between less than, greater than, and area between graphs.); 2. Use the Central Limit Theorem to find s and ag: 3. Calculate the z-score for 253 and move the slider along the e-axis to the appropriate z-score 4. The purple area under the curve represents the probability of the event occurring. Interpret the purple area under the curve. Round your answers to two decimal places
Answers
The probability that the average laptop warranty purchase for the sample will be greater than 253 is 0.0314
We can use the central limit theorem to approximate the distribution of the sample mean, which follows a normal distribution with a mean of 243 and a standard deviation of 34/sqrt(40) = 5.38.
Then, we can standardize the value of interest (253) using the formula
z = (x - mu) / (sigma / sqrt(n))
where x is the value of interest (253), mu is the population mean (243), sigma is the population standard deviation (34), and n is the sample size (40).
z = (253 - 243) / (34/sqrt(40)) = 1.86
Using a standard normal distribution table or calculator, we can find the probability that a z-score is greater than 1.86. This probability is approximately 0.0314.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
The given question is incomplete, the complete question is:
A technology company is studying the launch of their new laptop computers in order to track warranty purchases. Assume that the laptop warranties have an unknown distribution with a mean of 243 days and a standard deviation of 34 days. A sample of 40 laptop warranty purchases are randomly selected from the population. What is the probability that the average. laptop warranty purchase for the sample will be greater than 253?
A carpenter needs 9.3 feet of rope for a project. How much will the carpenter spend if the rope costs $3.82 per foot?
O $35.53
O$44.84
O$45.84
O $355.30
Answers
The total amount the carpenter will spend if the rope costs $3.82 per foot is $35.526
How to determine how much will the carpenter spend if the rope costs $3.82 per foot?The length of rope is given as:
Length = 9.3 feet
The price per rope is given as:
Price per rope = $3.82 per foot
The total amount spent by the carpenter is calculated as:
Total amount = Length * Price per rope
Substitute the known values in the above equation
Total amount = 9.3 feet * $3.82 per foot
Evaluate the product
Total amount = $35.526
Hence, the total amount the carpenter will spend if the rope costs $3.82 per foot is $35.526
Read more about products at:
https://brainly.com/question/10873737
#SPJ1
Answer:
A) $35.53
===================
Given:The cost of the rope is $3.82 per foot,The length of the rope is 9.3 feet.Money spent is:$3.82 * 9.3 = $35.526 ≈ $35.53 (rounded)Correct choice is A.
Which equations are equivalent to Negative one-fourth (x) + three-fourths = 12 Select all that apply. (StartFraction negative 4 x over 1 EndFraction + three-fourths = 12 Negative 1 (StartFraction x over 4 EndFraction) + three-fourths = 12 StartFraction negative x + 3 over 4 EndFraction = 12 One-fourth (x + 3) = 12 (StartFraction negative x over 4 EndFraction + three-fourths = 12
Answers
The equations which are equivalent to Negative one-fourth (x) + three-fourths = 12 are:
Negative 1 (StartFraction x over 4 EndFraction) + three-fourths = 12
StartFraction negative x + 3 over 4 EndFraction = 12
(StartFraction negative x over 4 EndFraction + three-fourths = 12
Given equation is,
Negative one-fourth (x) + three-fourths = 12
This can be written numerically as,
-1/4 x + 3/4 = 12
-x/4 + 3/4 = 12, which is the last option.
This can be written as,
-1 (x/4) + 3/4 = 12, which is the second option.
Since the denominators are same in left hand side, adding the fractions, we get,
(-x + 3) / 4 = 12, which is the third option.
Hence the second, third and last options are equivalent equations.
Learn more about Equivalent Equations here :
https://brainly.com/question/29013156
#SPJ1
The weights X of an animal are distributed according to the
probability distribution shown.
What is the probability that the animal's weight will be less than
151 pounds?
O 0.25
O 0.50
O 0.60
O 0.75
Answers
The probability that the animal's weight will be less than 151 pounds is 0.50.
The correct option is B.
What is the probability that the animal's weight will be less than 151 pounds?Since the given probability distribution ranges from 148 to 152, and we need to find the probability that the animal's weight will be less than 151 pounds, we can add the probabilities corresponding to the weights less than 151.
From the distribution, we see that the probability of the animal's weight being less than 151 pounds is 0.2 + 0.3 = 0.5.
Therefore, the answer is O 0.50.
Learn more about probability at: https://brainly.com/question/251701
#SPJ1
How Much would you have to invest today to receive $6,000 each year for 10 years at 9 percent?
Answers
You have to invest $31,579 today to get $6,000 each year for 10 years at 9 percent.
What is Simple Interest?Simple interest is defined as the interest obtained over the principal amount on a certain rate.
Given that,
Number of years, n = 10 years
Rate of interest, r = 9% = 0.09
Amount received each year = $6,000
Amount received in 10 years = $6,000 × 10 = $60,000
Final amount, A = $60,000
To find the principal amount that you invest today,
A = P (1 + rt)
60,000 = P(1 + (0.09 × 10))
60,000 = P (1.9)
P = 60,000 / 1.9
P = 31578.947 ≈ 31,579
Hence the amount to invest today is $31,579.
Learn more about Simple Interest here :
https://brainly.com/question/28978701
#SPJ1
The product of a number and negative three is twenty-seven. Which of the following could represent this statement?
A. -3n + 27
B. -3(27) = n
C. -3n = 27
D. -3 = 27n
Answers
Answer:
C
Step-by-step explanation:
If that's wrong it's D
Answer:
C.
Step-by-step explanation:
If it is a product, that is a way to say that it is multiplication. Since the product is 27, the answer is 27. So what multiplied by -3 equals to 27? To write this, you have to multiply -3 by n to get 27.
Write a real world situation the would represent -5 + -2 +3 = -4
Answers
How to find an inverseF(x) = 3x - 1 solve for Y
Answers
Answer:
f^-1(x) = x/3 + 1/3
Explanation:
We were given that:
\(f(x)=3x-1\)We are to calculate the inverse of the function above. We will do so by following the steps enumerated below:
I. We will replace f(x) with ''y'', we have:
\(\begin{gathered} f(x)=3x-1 \\ f(x)=y \\ \Rightarrow y=3x-1 \\ \\ \therefore y=3x-1 \end{gathered}\)II. We will replace the position of ''x'' with ''y'' and ''y'' with ''x''. We have:
\(\begin{gathered} y=3x-1\rightarrow x=3y-1 \\ x=3y-1 \\ \\ \therefore x=3y-1 \end{gathered}\)III. We will proceed to make ''y'' the subject of the formula, we have:
\(\begin{gathered} x=3y-1 \\ \text{Add ''1'' to both sides, we have:} \\ x+1=3y\Rightarrow3y=x+1 \\ 3y=x+1 \\ \text{Divide through by ''3'' to obtain ''y'', we have:} \\ y=\frac{1}{3}x+\frac{1}{3} \\ \\ \therefore y=\frac{1}{3}x+\frac{1}{3} \end{gathered}\)IV. We will now replace ''y'' with the inverse symbol, we have:
\(\begin{gathered} y=\frac{1}{3}x+\frac{1}{3} \\ y\rightarrow f^{-1}(x) \\ f^{-1}(x)=\frac{1}{3}x+\frac{1}{3} \\ \\ \therefore f^{-1}(x)=\frac{1}{3}x+\frac{1}{3} \end{gathered}\)We will now proceed to verify the answer obtained in IV. above. We have:
\(\begin{gathered} \mleft({f\circ{f^{-1}}}\mright)\mleft(x\mright)=f\lbrack f^{-1}(x)\rbrack \\ ({f\circ{f^{-1}}})(x)=f(\frac{1}{3}x+\frac{1}{3}) \\ ({f\circ{f^{-1}}})(x)=3(\frac{1}{3}x+\frac{1}{3})-1 \\ ({f\circ{f^{-1}}})(x)=x+1-1 \\ ({f\circ{f^{-1}}})(x)=x \\ \\ \therefore The\text{ answer obtained in IV. is correct} \end{gathered}\)Therefore, the inverse of the function is: f^-1(x) = x/3 + 1/3
A camera crew on the ground is recording the act of a performer walking a tightrope stretched between two buildings. A member of the camera crew who is 1.8 m tall is almost directly below one end of the tightrope. When the performer steps out onto the other end of the tightrope, the angle of elevation is 75 . If the buildings are 30 m apart, how many meters above the ground is the performer?
Answers
Answer:
32332
Step-by-step explanation:
Please help. I’ll mark you as brainliest if correct!

Answers
Answer:
When x = -1/4 and when x = -15/4
Step-by-step explanation:
The x intercept will be when f(x)=0, so
0 = 4|x+2| -7
7 = 4|x+2|
|x+2|=7/4 here you have to cases
case 1
x+2=7/4
x=7/4-2
x=-1/4 = -0.25
case 2
x+2 = -7/4
x = -2-7/4
x = -15/4 = -3.75
please help meeee i am lost

Answers
Answer:
The sum of a sequence is known as a series. Thus means a harmonic series is infinite with no limit
can someone help me with this

Answers
Answer:
31°
Step-by-step explanation:
If ∠dab=55° and ∠cab=24° and ∠cab+∠dac=∠dab then all you need to do is subtract 55° and 24° to get 31°
which is equal to (sinx+cosx)^2+(sinx-cosx)^2 using identities?
Answers
The expression (sinx + cosx)^2 + (sinx - cosx)^2 simplifies to
4 + 2sinxcosx.How to simplify the identityTo simplify the expression (sinx + cosx)^2 + (sinx - cosx)^2 using trigonometric identities, we can expand and simplify the expression.
Expanding the squared terms
(sin^2x + 2sinxcosx + cos^2x) + (sin^2x - 2sinxcosx + cos^2x)
Using the trigonometric identity sin^2x + cos^2x = 1, we can simplify further:
(1 + 2sinxcosx + 1) + (1 - 2sinxcosx + 1)
Simplifying the expression, we have:
2 + 2sinxcosx + 2
Combining like terms, we get:
4 + 2sinxcosx
Learn more about identities at
https://brainly.com/question/7331447
#SPJ1
Find the missing angle measure. Show work.
17.
7
20
24
Solve the remaining parts of the triangle.
19.
B
38
12.5 C
7
13
17.
18.
19, AC=
AB-
mzB
Need help with all these please. Asap urgent help need this done before Monday

Answers
To find the missing angle measure, we need to use the fact that the sum of angles in a triangle is 180 degrees. Let's denote the missing angle as x. We know that one angle is 38 degrees and another angle is 12.5 degrees.Therefore, the missing angle measure is 129.5 degrees.
By subtracting these two angles from 180 degrees, we get:
180 - 38 - 12.5 = 129.5
Without additional information, it is not possible to determine the remaining parts of the triangle. We would need the lengths of at least one side or the measures of other angles to solve for the missing parts.
The given information states that AC is equal to AB minus mzB. Without knowing the values of AB and mzB, we cannot determine the exact length of AC. We would need additional information to solve for the length of AC.Therefore, the missing angle measure is 129.5 degrees.
For more such questions on angle
https://brainly.com/question/30759856
#SPJ11
Use the following function to complete this question:
f(x)=(x-1)^3+5
Graph the function and fill in the blanks.
If the transformation listed is not applicable write none.
Fill in the blanks in the form:
4 left
5 up
Write infinity in the form: inf
Horizontal shift:
Vertical shift:
Vertical stretch factor:
Vertical compression factor:
Axis of reflection:
Domain:
Range:
Inflection Point:
Pic is attached below

Answers
The following is deduced from the equation f(x)=(x - 1)^3 + 5
Horizontal shift: 1 left
Vertical shift: 5 down
Vertical stretch factor: 1
Vertical compression factor: 1
Axis of reflection: -x + 6
Domain: all real numbers
Range: all real numbers
Inflection Point: (1, 5)
What is vertical stretch factor?The vertical stretch factor is a term used in mathematics to describe the transformation that changes the height of a graph while leaving the horizontal axis unchanged. In other words, it's a factor by which the y-values of a function are multiplied to produce a new, stretched or compressed version of the original graph.
The stretch factor is usually represented by the symbol "k". For example, if the equation of a function is y = f(x), then the equation of its vertically stretched image would be y = k * f(x). A positive value of k stretches the graph upward, while a negative value of k compresses the graph downward. If k > 1, the graph is stretched vertically; if 0 < k < 1, the graph is compressed vertically; if k = 1, the graph remains unchanged.
Learn more about vertical stretch factor:
https://brainly.com/question/28353408
#SPJ1
What is the value of y in 8 + (6/y) = 53 ?
Answers
Answer:
y=2/15
Step-by-step explanation:
8+(6/y)=53
We move all terms to the left:
8+(6/y)-(53)=0
Domain of the equation: y)!=0
y!=0/1
y!=0
We add all the numbers together, and all the variables
(+6/y)+8-53=0
We add all the numbers together, and all the variables
(+6/y)-45=0
We get rid of parentheses
6/y-45=0
We multiply all the terms by the denominator
-45*y+6=0
We add all the numbers together, and all the variables
-45y+6=0
We move all terms containing y to the left, all other terms to the right
-45y=-6
y=-6/-45
y=2/15
hope this helps.
Functions and their Properties
Practice
Need help

Answers
Answer:
\(g(n-7)=\frac{n^{2}-14n+43}{7n-49}\) → (a)
Step-by-step explanation:
We need to evaluate g(n - 7), where
\(g(x)=\frac{x^{2}-7}{7x}\)Replace x by (n - 7) to evaluate it
∵ x = (n - 7)
∴ \(g(n-7)=\frac{(n-7)^{2}-6}{7(n-7)}\)
→ Let us find (n - 7)²
∵ (n - 7)² = (n - 7)(n - 7) = (n)(n) + (n)(-7) + (-7)(n) + (-7)(-7)
∴ (n - 7)² = n² + (-7n) + (-7n) + 49 = n² + -14n + 49
∴ (n - 7)² = n² - 14n + 49
→ Find 7(n - 7)
∵ 7(n - 7) = 7(n) - 7(7)
∴ 7(n - 7) = 7n - 49
→ Now let us write then in the form above
∵ \(g(n-7)=\frac{n^{2}-14n+49-6}{7n-49}\)
→ Add the like terms in the numerator
∴ \(g(n-7)=\frac{n^{2}-14n+43}{7n-49}\)
The correct answer is (a)
Using sum/difference trigonometry identies

Answers
Answer:
π.
Step-by-step explanation:
1) to simplify the given expression:
\(2sin[0.5*( \theta +\frac{ \pi}{6} + \theta-\frac{7 \pi}{6} )]*cos[0.5( \theta+\frac{ \pi}{6} - \theta+\frac{7 \pi}{6})]=-1\)
\(2sin[ \theta-\frac{ \pi}{2}]cos\frac{2 \pi}{3}=-1;\\sin[ \theta-\frac{ \pi}{2}]=1;\)
2) to resolve the simplified equation:
\(\theta= \pi +2 \pi*n, \ n-Z.\)
3) to calculate the number of the required solutions on [0; 2п):
when n=0 x=п - included in [0;2п)
when n=-1 x=-п - non-included in [0;2п)
4) finally, x=п.
(12sin(pi/2x)*lnx)/((x³+5)(x-1))
lim as x approaches 1
Answers
The limit of the given function as x approaches 1 is 0.
To find the limit of the given function as x approaches 1, we need to evaluate the expression by substituting x = 1. Let's break it down step by step:
1. Begin by substituting x = 1 into the numerator:
\(\[12\sin\left(\frac{\pi}{2}\cdot 1\right)\ln(1) = 12\sin\left(\frac{\pi}{2}\right)\ln(1) = 12(1)\cdot 0 = 0\]\)
2. Now, substitute x = 1 into the denominator:
(1³ + 5)(1 - 1) = 6(0) = 0
3. Finally, divide the numerator by the denominator:
0/0
The result is an indeterminate form of 0/0, which means further analysis is required to determine the limit. To evaluate this limit, we can apply L'Hôpital's rule, which states that if we have an indeterminate form 0/0, we can take the derivative of the numerator and denominator and then evaluate the limit again. Applying L'Hôpital's rule:
4. Take the derivative of the numerator:
\(\[\frac{d}{dx}\left(12\sin\left(\frac{\pi}{2}x\right)\ln(x)\right) = 12\left(\cos\left(\frac{\pi}{2}x\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{-1}{x} + \frac{\sin\left(\frac{\pi}{2}x\right)\ln(x)}{x}\right)\]\)
5. Take the derivative of the denominator:
\(\[\frac{d}{dx}\left((x^3 + 5)(x - 1)\right) = \frac{d}{dx}\left(x^4 - x^3 + 5x - 5\right) = 4x^3 - 3x^2 + 5\]\)
6. Substitute x = 1 into the derivatives:
Numerator: \(\[12\left(\cos\left(\frac{\pi}{2}\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{-1}{1} + \sin\left(\frac{\pi}{2}\right) \cdot \frac{\ln(1)}{1}\right) = 0\]\)
Denominator: 4(1)³ - 3(1)² + 5 = 4 - 3 + 5 = 6
7. Now, reevaluate the limit using the derivatives:
lim as x approaches 1 of \(\[\frac{{12\left(\cos\left(\frac{\pi}{2}x\right) \cdot \left(\frac{\pi}{2}\right) \cdot \frac{{-1}}{{x}} + \sin\left(\frac{\pi}{2}x\right) \cdot \frac{{\ln(x)}}{{x}}\right)}}{{4x^3 - 3x^2 + 5}}\]\)
= 0 / 6
= 0
Therefore, the limit of the given function as x approaches 1 is 0.
For more such questions on L'Hôpital's rule
https://brainly.com/question/24116045
#SPJ8
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
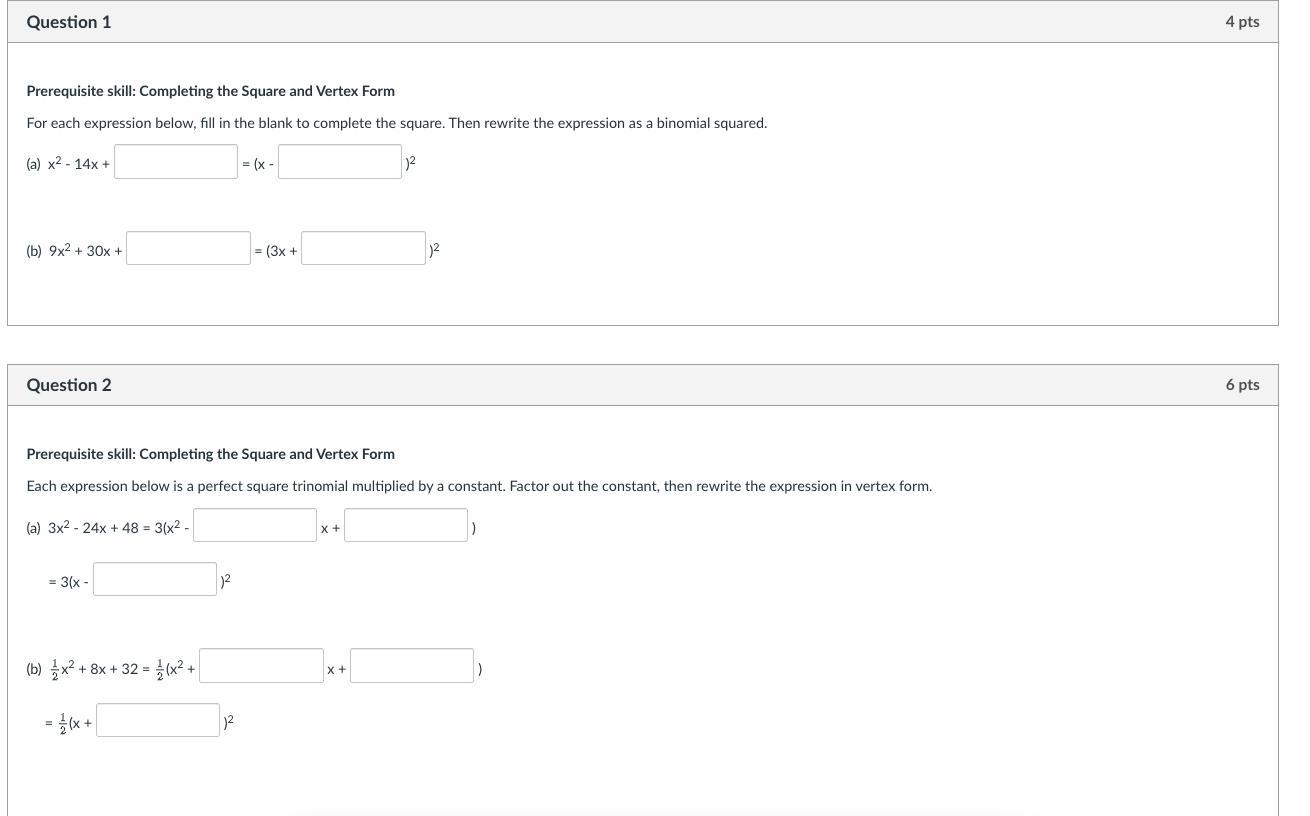
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
What is the value of y?

Answers
Answer:
Step-by-step explanation:
Remark
The value of the y can be found by using the Geometric Mean. To use the said mean, you must compare parts of one triangle to parts of the second triangle. In this case, the small triangle containing boy 4 and y, must be compared to the triangle use y and 12
Formula
This translates to
4 / y = y/12
Explanation. The two triangles y and 4 and y and 12 are similar. The short side on the small right triangle on the left is 4. The second longest side on the same triangle is y.
In the triangle containing y and 12 The short side is y and the second side length is 12. You have to read this a couple of times to get the meaning of the two ratios.
Solution
4/y = y / 12 Cross multiply
y^2 = 4 * 12
y^2 = 48 Take the square root of both sides.
√y^2 = √48
y = √2 * 2 * 2 * 2 * 3
y = 2 * 2 * √3
Answer
y = 4√3
Answer:
y = 4√3 y = 4√3
Step-by-step explanation:
i hope it's help
The IQ scores and science test scores of fourth grade students is given by the line of best fit ŷ = −20.3 + 0.7489s, where ŷ is the predicted science score and s is the IQ score. An actual science test score for a student is 52.6 with an IQ of 100.
Find and interpret the residual.
−1.99; The line of best fit underpredicts the student's science test score.
1.99; The line of best fit overpredicts the student's science test score.
1.99; The line of best fit underpredicts the student's science test score.
−1.99; The line of best fit overpredicts the student's science test score.
Answers
-19.99; The line of best fit underpredicts the student's science test score.
So correct option is A.
What do you mean by prediction?A prediction is an estimation or forecast about future events or conditions, based on past data and trends, current information, and/or mathematical models. Predictions can be made in various fields, such as finance, weather, sports, social sciences, and natural sciences. The accuracy of predictions depends on many factors, including the quality of the data used, the assumptions made, the complexity of the system being analyzed, and the reliability of the methods used. Predictions are not always accurate and are often subject to revision as new information becomes available.
The predicted science score for the student with IQ 100 can be calculated using the line of best fit:
ŷ = −20.3 + 0.7489 * 100 = 71.59
The residual is the difference between the actual science test score and the predicted science score:
residual = actual score - predicted score = 52.6 - 71.59 = -19.99
So the line of best fit underpredicts the student's science test score by 19.99 points.
Therefore, the residual is:
-19.99; The line of best fit underpredicts the student's science test score.
To know more about residual visit:
https://brainly.com/question/7467603
#SPJ1
How many feet are in half a mile?
Answers
Answer:
answer below:)
Step-by-step explanation:
There are 5280 feet in one mile. So, half a mile is equal to 0.5 x 5280 = 2640 feet.
Approximate when the function y = -x² + 3x + 4 is negative.
-2
8
9
0 x < -1
2
0 -1
0 x>4
x²+3x+4
6 x
27
4
Answers
The function y = -x² + 3x + 4 is negative when - 1 > x > 4.
A function is made up of three parts: a set of inputs, a set of outputs, and a rule that links the components of the input set to the components of the output set so that each input is paired with exactly one output.
Consider the function,
y = - x² + 3x + 4
For the function to be negative y < 0.
Therefore,
- x² + 3x + 4 < 0
- ( x² - 3x - 4 ) < 0
- ( x² - 4x + x - 4 ) < 0
- [ x ( x - 4 ) + 1 ( x - 4 ) ] < 0
- ( x + 1 ) ( x - 4 ) < 0
Multiplying by -1 on each side of the inequality.
- ( x + 1 ) ( x - 4 )(-1) > 0( - 1 )
( x + 1 ) ( x - 4 ) > 0
x < - 1 or x > 4
Therefore, the function is negative when - 1 > x > 4.
Learn more about function here:
https://brainly.com/question/11624077
#SPJ9
In a party, the first time the door bell rang, 6 guest arrived. On each succeeding ring, two more guests arrived than on the previous ring. After 10 rings, what was the number of guests at the party?
answer choices;
A. 21
B. 31
C. 29
D. 24
E. 28
Answers
