Solve for x: 2(x+3)+2=4x-12
Answers
Answer:
x = 10
Step-by-step explanation:
Our equation is: 2(x+3)+2 = 4x - 12
Distribute: 2x+6+2 = 4x - 12
Combine like terms: 2x + 8 = 4x - 12
Rearrange terms: 8 + 12 = 4x - 2x
Simplify: 20 = 2x
Therefore: x = 10
Related Questions
The base of a parallelogram measure 1 m 60 cm and height is 75 cm find the area in m square
Answers
Answer:
1.44 meters squared
Step-by-step explanation:
area = h · b
1.60 * 0.75 = 1.2
1.2 * 1.2 ( to find area in m square ) = 1.44
help pls last question
The relationship between the number of days and
the height of a banana tree represents a linear
function because the banana tree's growth is
constant. Alani works at the garden center and
wants to write an equation to track the height of the
banana tree after d days. She writes the following
equation:

Answers
The equation allows us to chart the tree's development over time and forecast its ultimate height.
what is function ?A function is a mathematical formula that allots each input from one set, known as the domain, to precisely one output from another set, known as the range. A function can be used to model relationships between variables, answer issues, and make predictions. It can be represented by an equation, a graph, a table, or a verbal description. Numerous branches of mathematics, as well as disciplines like physics, engineering, finance, and computer science, make extensive use of functions. Typical instances of functions include: When a function is graphed, it always changes at the same rate and forms a straight line. They are frequently used to simulate relationships between two variables that are related linearly, such as time and location.
given
After d days, Alani created the following algorithm to measure the height of the banana tree:
h = d + 8
Since this function is linear, the banana tree's development will remain constant over time. According to the calculation, the tree starts out at a height of 8 units, and it increases by 1 unit per day after that.
We can enter a figure for d (the number of days) and solve for h using this equation (the height of the tree after d days). For instance, we can enter d = 10 into the calculation to get the height of the tree after 10 days:
h = 10 + 8
h = 18
Therefore, the altitude of the banana plant after 10 days would just be 18 units. This equation allows us to chart the tree's development over time and forecast its ultimate height.
To know more about function visit:
https://brainly.com/question/28193995
#SPJ1
Please help need by tomorrow it would be very very very appreciated

Answers
The solution of the given system of equations is (8, -1). of the given system of equations is (8, -1).
One method to solve the given system of equations is substitution:
- Solve one of the equations for one of the variables (e.g., x = 9 + y from the second equation).
- Substitute the expression for the variable into the other equation.
- Solve the resulting equation for the remaining variable.
- Substitute the value for the remaining variable back into one of the original equations to find the value of the other variable
Using this method with the given equations
- x - y = 9 -> x = 9 + y
- 3x + 2y = 22 -> 3(9 + y) + 2y = 22
- Simplifying and solving for y: 27 + 5y = 22 -> 5y = -5 -> y = -1
- Substituting y = -1 into x = 9 + y: x = 8
To check this solution, we can substitute these values back into both original equations and confirm that they are true statements.
For such more questions on solution
https://brainly.com/question/24644930
#SPJ8
The tables represent the functions f(x) and g(x). f(x) -5 -2 -1 0 1 2 -3 -1 1 3 w 5 X -3 -2 -1 0 1 2 g(x) -13 -9 -5 -1 3 7 Which input value produces the same output value for the two functions? x = -3 O x = -1 x = 0 Ox=1 The tables represent the functions f ( x ) and g ( x ) . f ( x ) -5 -2 -1 0 1 2 -3 -1 1 3 w 5 X -3 -2 -1 0 1 2 g ( x ) -13 -9 -5 -1 3 7 Which input value produces the same output value for the two functions ? x = -3 O x = -1 x = 0 Ox = 1

Answers
Answer:
x=1
Step-by-step explanation:
There are two functions (f & g), each of which have a table of inputs and outputs. The same list of inputs is given to both functions, but the outputs are different.
Imagine that you asked your Father 6 questions, (weirdly instead of numbered 1 through 6, numbered -3 through 2), and that he gave you a list of answers.
Imagine that you asked your Grandfather the same 6 questions, and you got a list of answers from him.
On which question did they give the same answer?
It was on question number "1", (really the 5th question, but as we've numbered things from -3 to 2, it's question "1").
Since the "questions" were the input, "x", x=1.
Find the area of the given triangle. Round the area to the same number of significant digits given for each of the given sides. a = 22.8, B = 47.49, C = 62.4°
Answers
The area of the given triangle is approximately 213.6 square units.
How to find the area of the given triangle for each of the given sides?To find the area of the given triangle with sides a = 22.8, angle B = 47.49°, and angle C = 62.4°, follow these steps:
1. First, find angle A using the angle-sum property of a triangle, which states that the sum of angles in a triangle equals 180°. Therefore,
angle A = 180° - angle B - angle C.
A = 180° - 47.49° - 62.4°
A ≈ 70.11°
2. Next, use the sine rule to find the length of side b. The sine rule states that (a/sin A) = (b/sin B). Rearrange the formula to solve for b:
b = (a * sin B) / sin A
b = (22.8 * sin(47.49°)) / sin(70.11°)
b ≈ 19.6
3. Now that you have the lengths of two sides (a and b) and the included angle (C), you can use the formula for the area of a triangle, given by:
Area = 0.5 * a * b * sin C
Area = 0.5 * 22.8 * 19.6 * sin(62.4°)
Area ≈ 213.6
Therefore, the area of the given triangle is approximately 213.6 square units, rounded to the same number of significant digits as the given sides.
Learn more about triangle
brainly.com/question/2773823
#SPJ11
a continuous random variable x has a normal distribution with a mean of 73 and a standard deviation of 14. in the sampling distribution of the sample mean for a sample of 16 elements, what is the z-score for a sample mean of 65.30?
Answers
z-score for a sample mean of 65.30 is 60.085.
Z-scores are calculated using the formula z = (x-)/, where x represents the raw score, the population mean, and the population standard deviation. The z-score is simply the raw score less the population mean, divided by the population standard deviation, as the calculation demonstrates.
What is standard deviation?When the standard deviation is low, the data are concentrated around the mean, and when it is large, the data are widely dispersed. ou Score, Mean, and Standard Deviation are expressed as Z Z= 65.30-73/14sZ=60.085.Standard deviation is important because it makes measurements easier to understand when the data is dispersed. The more equally distributed the data is, the bigger the standard deviation of the data will be.A z-score determines the distance between a data point and the mean using standard deviations. Z-scores may be positive or negative. The sign indicates whether the observation is above or below the mean.To learn more about standard deviation refer to:
https://brainly.com/question/475676
#SPJ4
what is the measure of GAB
Answers
Answer:
180°
Step-by-step explanation:
the measure of GAB is 180°
Answer:
TRUBOMAT GAB measures the turbidity of liquid applying nephelometric method. For this purpose, a combined transmitted & scattered beams measurements are used, in which a transmitter and a receiver face each other and another transmitter is arranged orthogonally (at an angle of 90 °).
please mark as brainliest
EXAMPLE: Standard Deviation
Find the standard deviation of the sample
1, 2, 8, 11, 13
Data Value...........1........2......8.....11......13
Deviation............-6.....-5......1.......4......6
(Deviation)2.......36....25.....1......16....36
Answers
The standard deviations that is square root of variance of a sample of data values 1, 2, 8, 11, 13 is equals to the 4.774.
Standard deviation is a statistical measures that is used to deviations of a dataset relative to its mean and is calculated as the square root of the variance. Steps to determine the standard deviations are the following:
Determine the mean of values. For each data value, determine the square of its distance to the mean.Sum the resultants obtained from Step 2.Divide by the number of data values.Take the square root.Formula for standard deviations is
\(\sigma = \sqrt {\frac{ \sum( x_i - \mu)²}{ n }}\)
Where, xᵢ --> observed values
μ--> mean
n --> total number of observations
Now, We have a data set of data values 1, 2, 8, 11, 13. We have to determine the standard deviations for this data set. Now
Mean of data values, \(= \frac{1 + 2 + 8 + 11 + 13 }{5}\)= 7deviations of observed values from mean value, that is \(( x_i- \mu) \) are, - 6, -5, 1, 4, 6 and sum of square of deviations is equals 36 + 25 + 1 + 16 + 36 = 114.Now, plug all known values in above formula, \(\sigma = \sqrt {\frac{ 114}{ 5}}\) = 4.774
Hence, required value is 4.774.
For more information about standard deviations, visit:
https://brainly.com/question/30403900
#SPJ4
What is the formula for the pythagorem theory
Answers
Answer:
C^2 = a^2 + b^2
The formula for the pythagorem theory
a suspension bridge with weight uniformly distributed along its length has twin towers that extend meters above the road surface and are meters apart. the cables are parabolic in shape and are suspended from the tops of the towers. the cables touch the road surface at the center of the bridge. find the height of the cables at a point meters from the center.
Answers
The height of the cable is 0.15 meters and 1.35 meters at a point 200 meters and -200.
The given details are: Height of twin towers above road surface = h = 160 meters. Distance between twin towers = d = 800 meters. At the center of the bridge, the cables touch the road surface so the maximum height of the cable will be h. Using the formula for the parabolic cable we get: h(x) = a(x - d/2)(x + d/2). Let's find the value of "a" using the maximum height of the cable at the center of the bridge .i.e., h = a(0 - d/2)(0 + d/2) => h = a(d/2)^2 => a = (4h/d^2)Therefore, h(x) = (4h/d^2)(x - d/2)(x + d/2)We need to find the height of the cables at a point x meters from the center. Therefore, we need to find the value of h(x) when x = ±200 meters from the center of the bridge. h(x) = (4h/d^2)(x - d/2)(x + d/2) => h(x) = (4 × 160)/(800 × 800) (x - 800/2)(x + 800/2)When x = -200,h(-200) = (4 × 160)/(800 × 800) (-200 - 800/2)(-200 + 800/2)= (4 × 160)/(800 × 800) (-1200)(200)h(-200) = 0.15 meters. When x = 200,h(200) = (4 × 160)/(800 × 800) (200 - 800/2)(200 + 800/2)= (4 × 160)/(800 × 800) (-400)(1200)h(200) = 1.35 meters. Hence, the height of the cable is 0.15 meters and 1.35 meters at a point 200 meters and -200 meters from the center of the bridge respectively.
Learn more about Height
brainly.com/question/10726356
#SPJ11
find the general solution of the system bold x prime(t)equalsax(t) for the given matrix a.
Answers
The general solution of the system x'(t) = Ax(t), where A is the given matrix, can be found by solving the system of linear differential equations associated with it.
To find the general solution, we need to solve the system of linear differential equations x'(t) = Ax(t), where x(t) is a vector-valued function and A is the given matrix.
The solution involves finding the eigenvalues and eigenvectors of the matrix A. The general solution will have the form x(t) = c₁v₁e^(λ₁t) + c₂v₂e^(λ₂t) + ... + cₙvₙe^(λₙt), where c₁, c₂, ..., cₙ are constants, v₁, v₂, ..., vₙ are eigenvectors, and λ₁, λ₂, ..., λₙ are eigenvalues of A.
This general solution represents a linear combination of exponential functions, where each term corresponds to an eigenvalue-eigenvector pair. The specific values of the constants are determined by initial conditions or boundary conditions provided in the problem.
Learn more about eigenvalues here:- brainly.com/question/29861415
#SPJ11
On a coordinate plane, Point C is at (-3,5) and Point D is at (4,9). What is the distance from point C to point D?
Answers
Answer:
5\(\sqrt[\\]{3} \\\) or about 8.66
Step-by-step explanation:
To find the distance of any line, you have to use distance formula.
\(\sqrt{(y-y_{1} )^{2} + (x-x_{1} )^{2}\)
So, we insert our points:
\(\sqrt{(5-9 )^{2} + (-3-4 )^{2}\)
Then you solve, and should end up with \(\sqrt{75}\). Either you can simplify it for an exact number, or you can round. It depends on what the directions ask for.
what is the surface area of a cylinder with a radius of 3 and a height of 1
Answers
Answer:
The surface area of a cylinder can be calculated using the formula:
SA = 2πr^2 + 2πrh
where r is the radius of the base of the cylinder, h is the height of the cylinder,
Substituting r = 3 and h = 1 into the formula, we get:
SA = 2π(3)^2 + 2π(3)(1)
SA = 2π(9) + 2π(3)
SA = 18π + 6π
SA = 24π
Therefore, the surface area of the cylinder is 24π square units.
The ratio of girls to total students at the YMCA summer camp is 6 to 10. If there are 900 students at the YMCA summer camp last summer, how many are girls?
Answers
Answer:
540 are girls
Step-by-step explanation:
6 to 10 means 6/10
900/10 = 90
90 x 6 = 540
Hi I need to know with equation is a one solution , no solution anf a infinite solution

Answers
The equation of a line in Slope-Intercept form is:
\(y=mx+b\)Where "m" is the slope and "b" is the y-intercept.
Let's write each equation given in the exercise as a System of equations and then let's write each equation in Slope-Intercept form. Then:
Equation 1 as a System of equations
\(\begin{cases}y=2(x-1)+6\Rightarrow y=2x-2+6\Rightarrow y=2x+4 \\ y=4x-22\end{cases}\)You can identify that the slope and the y-intercept of the first equation are:
\(\begin{gathered} m_1=2_{} \\ b_1=4 \end{gathered}\)And the slope and the y-intercept of the second equation are:
\(\begin{gathered} m_2=4 \\ b_2=-22 \end{gathered}\)Since:
\(\begin{gathered} m_1\ne m_2 \\ b_1\ne b_2 \end{gathered}\)The lines intersect each other and the System of equations has one solution.
Equation 2 as a System of equations
\(\begin{cases}y=6(2x+1)-2\Rightarrow y=12x+6-2\Rightarrow y=12x+4 \\ y=12x+4\end{cases}\)You can see that:
\(\begin{gathered} m_1=m_2 \\ b_1=b_2 \end{gathered}\)Therefore, since they are the same line, the system has infinite solutions.
Equation 3 as a System of equations
\(\begin{cases}y=2(4-x)\Rightarrow y=-2x+8 \\ y=-2(1+x)-2\Rightarrow y=-2-2x-2\Rightarrow y=-2x-4\end{cases}\)Since:
\(\begin{gathered} m_1=m_2 \\ b_1\ne b_2 \end{gathered}\)You can determine that the lines are parallel. Therefore, the System of equations has no solution.
The anwer is:
- The first equation has one solution.
- The second equation has infinite solutions.
- The third equation has no solution.
step 1
a) Suppose you are able to download 1 free song to your tablet daily and each additional download costs $0.59. If your monthly bill is $15.34, how many songs did you download if you downloaded 28 free songs? Write an equation and solve for the unknown variable.
b) Your uncle Jim lives in England, where the current exchange rate is 1.64 US dollars for each British pound. Solve for the amount of your monthly bill, to the nearest hundredth, if you lived in England.
c) If you had an additional 1.65 pounds to download songs, how many more songs could you have downloaded? Write and solve an equation to solve the problem. Describe the step-by-step process you used to solve the problem.
Answers
Answer:
a. 54
b. 9.35
Step-by-step explanation:
a. First, divide 15.34 by 0.59 to find the number of songs you had to pay for.
15.34/0.59 = 26
then add it to the number of free songs you downloaded
26 + 28 = 54
b. divide 15.34 by 1.64
15.34/1.64 = 9.35
for c I would just multiply 1.65 by the usd exchange rate (1.64) which is 2.10 so you could afford 3 more songs but I don't know what equation exactly you would use or if what I did works.
Ellen wants to put a down payment on a house in six years. She must accumulate $50,000 for the 10% down payment. Ellen puts X dollars in the bank now, X dollars after one year and X dollars after two years. How much should X be if the bank pays 5% interest, compounded annually? (b) [5 marks] After four years, the bank raises the interest it pays to 6% compounded annually. At the 6 year mark, Ellen takes $50,000 and uses it for the down payment and the rest is donated to a charity. How much is donated?
Answers
To calculate the value of X that Ellen should deposit in the bank, we need to determine the present value of the future payments that will accumulate to $50,000 in six years.
Using the formula for compound interest, the present value can be calculated as follows:
PV = X/(1 + r)^1 + X/(1 + r)^2 + X/(1 + r)^3,
where r is the annual interest rate (5%) expressed as a decimal.
To find the value of X, we set the present value equal to $50,000 and solve for X:
50,000 = X/(1 + 0.05)^1 + X/(1 + 0.05)^2 + X/(1 + 0.05)^3.
Once we determine the value of X, we can proceed to the next step.
For the second part of the question, after four years, the bank raises the interest rate to 6%.
From year four to year six, Ellen's money will continue to accumulate interest.
To find the amount donated, we calculate the future value of the remaining amount after deducting the down payment of $50,000:
Remaining amount = X/(1 + 0.06)^2 + X/(1 + 0.06)^3 + X/(1 + 0.06)^4.
The donated amount is then the difference between the remaining amount and the total accumulated after six years.
By evaluating these expressions, we can determine the value of X and the amount donated by Ellen.
Learn more about Compound Interest here:
brainly.com/question/12982348
#SPJ11
i need help asap this is urgent

Answers
Answer:
I
Step-by-step explanation:
I don't know love you tho
Sketching a Function from its Derivatives A In this post, you will use the first and second derivatives of a function (along with a few other pieces of information) to sketch the graph of a function. Sketch the graph of a single function f (x) that satisfies all of the following conditions. Use the techniques that we have learned in this course to do so. f'(x)= 16(x + 2) (6 - x) ³ 32(x + 6) f"(x) = (6 x - x) 4 The domain of fis (-[infinity], 6) U (6,[infinity]) x = 6 is a vertical asymptote of f lim f(x) = 1, lim f(x) = 1 x→→[infinity]0 f(2)= 1 8个
Answers
Here, x = 6 is a vertical asymptote of f, so the function approaches infinity as x approaches 6 from both sides.
Let's start by integrating f'(x) to get f(x). We have:
f'(x) = 16(x+2)(6-x)³ - 32(x+6)
Integrating both sides with respect to x:
f(x) = ∫[16(x+2)(6-x)³ - 32(x+6)] dx
Simplifying the integral, we get:
f(x) = -2(x+2)²(6-x)⁴ + 16(x+6) + C
where C is the constant of integration.
Next, we can find the critical points of f(x) by setting f'(x) = 0:
f'(x) = 16(x+2)(6-x)³ - 32(x+6) = 0
Solving for x, we get x = -2 and x = 6 as critical points.
Now, we can use the second derivative f''(x) to determine the concavity of the function. We have:
f''(x) = (6x-x)⁴ = x⁴
Since the second derivative is always positive for x > 0, the function is concave up on the interval (6, ∞).
Similarly, since the second derivative is always negative for x < 0, the function is concave down on the interval (-∞, -2).
At x = -2 and x = 6, the function has an inflection point.
Finally, we know that x = 6 is a vertical asymptote of f, so the function approaches infinity as x approaches 6 from both sides.
Learn more about the function visit:
https://brainly.com/question/11624077
#SPJ4
true or false The links in the blockchain that is created using an algorithm.
Answers
True, the links in the blockchain are created using an algorithm.
What is blockchain? Blockchain is a decentralized ledger technology that enables the secure exchange of digital assets across a network of participants without the need for a centralized authority or intermediary. The blockchain is created using an algorithm to secure the network and ensure that all transactions are transparent and verifiable.
In a blockchain, each block contains a cryptographic hash of the previous block, forming a chain of blocks (hence the name "blockchain"). The algorithm used to create the blockchain is a consensus algorithm, which ensures that all participants on the network agree on the same state of the ledger.
This consensus algorithm also ensures that no single participant can manipulate the ledger or change the contents of a block without being detected.
To know more about "cryptography" refer here:
https://brainly.com/question/88001#
#SPJ11
Number 11. I need help ??
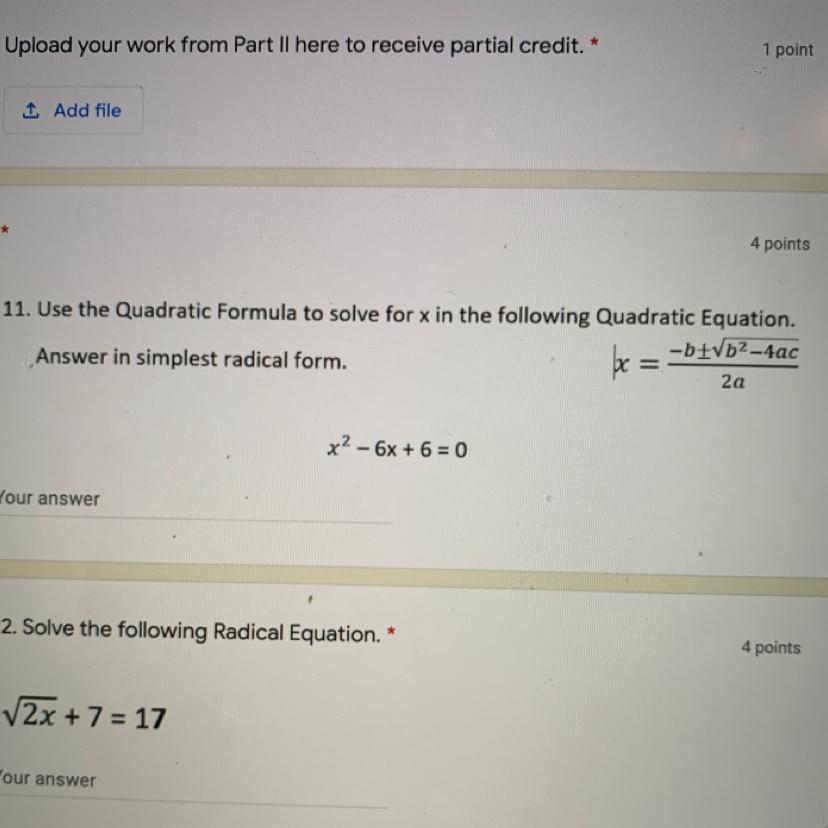
Answers
Answer: answering in simplest radical form, x = 3 ± √3
ASAP I need a quick answer pls

Answers
Answer:
62 square feet.
Step-by-step explanation:
7*5=35, 9*3=27, 35+27=62
a) Factor f(x)=−4x^4+26x^3−50x^2+16x+24 fully. Include a full solution - include details similar to the sample solution above. (Include all of your attempts in finding a factor.) b) Determine all real solutions to the following polynomial equations: x^3+2x^2−5x−6=0 0=5x^3−17x^2+21x−6
Answers
By using factoring by grouping or synthetic division, we find that \(x = -2\) is a real solution.
Find all real solutions to the polynomial equations \(x³+2x ²-5x-6=0\) and \(5x³-17x²+21x-6=0\).Checking for Rational Roots
Using the rational root theorem, the possible rational roots of the polynomial are given by the factors of the constant term (24) divided by the factors of the leading coefficient (-4).
The possible rational roots are ±1, ±2, ±3, ±4, ±6, ±8, ±12, ±24.
By substituting these values into \(f(x)\), we find that \(f(-2) = 0\). Hence, \(x + 2\) is a factor of \(f(x)\).
Dividing \(f(x)\) by \(x + 2\) using long division or synthetic division, we get:
-4x⁴ + 26x³ - 50x² + 16x + 24 = (x + 2)(-4x³ + 18x² - 16x + 12)Now, we have reduced the problem to factoring \(-4x³ + 18x² - 16x + 12\).
Attempt 2: Factoring by Grouping
Rearranging the terms, we have:
-4x³ + 18x² - 16x + 12 = (-4x^3 + 18x²) + (-16x + 12) = 2x²(-2x + 9) - 4(-4x + 3)Factoring out common factors, we obtain:
-4x³+ 18x² - 16x + 12 = 2x²(-2x + 9) - 4(-4x + 3) = 2x²(-2x + 9) - 4(3 - 4x) = 2x²(-2x + 9) + 4(4x - 3)Now, we have \(2x^2(-2x + 9) + 4(4x - 3)\). We can further factor this as:
2x²(-2x + 9) + 4(4x - 3) = 2x² (-2x + 9) + 4(4x - 3) = 2x²(-2x + 9) + 4(4x - 3) = 2x²(-2x + 9) + 4(4x - 3) = (2x² + 4)(-2x + 9)Therefore, the fully factored form of \(f(x) = -4x⁴ + 26x³ - 50x² + 16x + 24\) is \(f(x) = (x + 2)(2x² + 4)(-2x + 9)\).
Solutions to the polynomial equations:
\(x³ ³ + 2x² - 5x - 6 = 0\)Using polynomial division or synthetic division, we can find the quadratic equation \((x + 2)(x² + 2x - 3)\). Factoring the quadratic equation, we get \(x² + 2x - 3 = (x +
Learn more about synthetic division
brainly.com/question/28824872
#SPJ11
Divide (36z^2y^6-12z^6y^6) divided by (4z^5y^2)

Answers
The simplification of the equation is 9y⁴/z³ - 3zy⁴.
What is simplification?Simplifying procedures is one way to achieve uniformity in work efforts, expenses, and time. It reduces diversity and variety that is pointless, harmful, or unnecessary.
Solving a math problem is the same thing as simplifying an expression. You basically strive to write an expression as simply as you can when you simplify it. In conclusion, there shouldn't be any more multiplying, dividing, adding, or removing to do.
Here, we have
Given: (36z²y⁶-12z⁶y⁶)/(4z⁵y²)
We have to simplify this equation.
= (36z²y⁶-12z⁶y⁶)/(4z⁵y²)
= 36z²y⁶/4z⁵y² - 12z⁶y⁶/4z⁵y²
= 9y⁴/z³ - 3zy⁴
Hence, the simplification of the equation is 9y⁴/z³ - 3zy⁴.
To learn more about the simplification visit:
brainly.com/question/29168251
#SPJ1
Find the power set for the following sets (Write 3 examples of each)
a) Two sets A & B both having any 2 elements
b) Two sets A & B both having any 3 elements
c) Two sets A & B both having any 4 elements
Answers
Given statement solution is :- a) Power set for two sets A and B with any 2 elements:
Set A: {1, 2}, Set B: {3, 4}
Power set of A: {{}, {1}, {2}, {1, 2}}
Power set of B: {{}, {3}, {4}, {3, 4}}
b) Power set for two sets A and B with any 3 elements:
Set A: {1, 2, 3}, Set B: {4, 5, 6}
Power set of A: {{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
Power set of B: {{}, {4}, {5}, {6}, {4, 5}, {4, 6}, {5, 6}, {4, 5, 6}}
c) Power set for two sets A and B with any 4 elements:
Set A: {1, 2, 3, 4}, Set B: {5, 6, 7, 8}
Power set of A: {{}, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}}
Power set of B: {{}, {5}, {6}, {7}, {8}, {5, 6}, {5, 7}, {5, 8}, {6, 7}, {6, 8}, {7, 8}, {5, 6, 7}, {5, 6, 8}, {5, 7, 8}, {6, 7, 8},
a) Power set for two sets A and B with any 2 elements:
Set A: {1, 2}, Set B: {3, 4}
Power set of A: {{}, {1}, {2}, {1, 2}}
Power set of B: {{}, {3}, {4}, {3, 4}}
Set A: {apple, banana}, Set B: {cat, dog}
Power set of A: {{}, {apple}, {banana}, {apple, banana}}
Power set of B: {{}, {cat}, {dog}, {cat, dog}}
Set A: {red, blue}, Set B: {circle, square}
Power set of A: {{}, {red}, {blue}, {red, blue}}
Power set of B: {{}, {circle}, {square}, {circle, square}}
b) Power set for two sets A and B with any 3 elements:
Set A: {1, 2, 3}, Set B: {4, 5, 6}
Power set of A: {{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}
Power set of B: {{}, {4}, {5}, {6}, {4, 5}, {4, 6}, {5, 6}, {4, 5, 6}}
Set A: {apple, banana, orange}, Set B: {cat, dog, elephant}
Power set of A: {{}, {apple}, {banana}, {orange}, {apple, banana}, {apple, orange}, {banana, orange}, {apple, banana, orange}}
Power set of B: {{}, {cat}, {dog}, {elephant}, {cat, dog}, {cat, elephant}, {dog, elephant}, {cat, dog, elephant}}
Set A: {red, blue, green}, Set B: {circle, square, triangle}
Power set of A: {{}, {red}, {blue}, {green}, {red, blue}, {red, green}, {blue, green}, {red, blue, green}}
Power set of B: {{}, {circle}, {square}, {triangle}, {circle, square}, {circle, triangle}, {square, triangle}, {circle, square, triangle}}
c) Power set for two sets A and B with any 4 elements:
Set A: {1, 2, 3, 4}, Set B: {5, 6, 7, 8}
Power set of A: {{}, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}}
Power set of B: {{}, {5}, {6}, {7}, {8}, {5, 6}, {5, 7}, {5, 8}, {6, 7}, {6, 8}, {7, 8}, {5, 6, 7}, {5, 6, 8}, {5, 7, 8}, {6, 7, 8},
For such more questions on Power Sets Examples for Sets
https://brainly.com/question/33026825
#SPJ8
The perimeter of a rectangular garden is 48.8 feet it’s length is 12.4 what is it’s width
Answers
Answer:
12 feet
Step-by-step explanation:
Perimeter=l+l+w+w
48.8=12.4+12.4+2w
48.8=24.8+2w
2w=24, w=12 feet
14. The table shows the survey results of exercises
people do regularly.
Which is true based on the table?

Answers
Answer:
Answers in the question are A, B, and E.
The answers to the table are:
yes no total
yes: 12 25 37
no: 12 6 18
total: 24 31 55
Hopefully this helped, sorry if I was too late :)
A punch recipe requires 4 cups of lemonade to make 7 gallons of punch. Using the same recipe, what is the amount of lemonade needed for 1 gallon of punch? Answer please!
Answers
Answer:1.75
for each gallon we need to find the rate of each.So 7 gallons takes 4 cups.We will divide the 7 gallons over the 4 cups.
7/4=1.75
1.75 cups of lemonade for each gallon
a student on the 20 m line of a metric football field kicks a football at an angle of 53 with an initial velocity of 25 m/s find the time the football is in the air, what meter line the football lands on and the ball's maximum height
Answers
The time the football is in the air is approximately 4.07s and the football lands on or around the 81.23meter line. the ball's maximum height is approximately 20.33 meters.
How can we calculate the time of flight at an angle with a given initial velocity?
The time of flight can be calculated using the equation:
\(\frac{(2 * initial velocity * sin(angle))}{gravitational acceleration}\). The meter line the football lands on can be found by calculating the horizontal distance traveled using the equation (initial velocity * cos(angle) * time of flight). The maximum height can be determined using the formula \(\frac{ (initial velocity^2 * sin^2(angle)) }{(2 * gravitational acceleration)}\).
To find the time the football is in the air, the meter line it lands on, and the ball's maximum height, we can use the equations of motion for projectile motion.
1.Time of flight:
The time the football is in the air can be determined using the formula:
Time of flight = \(\frac{(2 * initial velocity * sin(angle))}{gravitational acceleration}\)
Given:
Initial velocity (u) = 25 m/s
Angle (θ) = 53°
Gravitational acceleration (g) = 9.8 m/s²
Time of flight =\(\frac{(2 * 25 * sin(53\°))}{9.8}\)
≈ 4.07 seconds
Therefore, the time the football is in the air is approximately 4.07 seconds.
2.Meter line the football lands on: To determine the meter line the football lands on, we need to calculate the horizontal distance traveled by the football.
Horizontal distance = initial velocity * cos(angle) * time of flight
Horizontal distance = 25 * cos(53°) * 4.07
≈ 61.23 meters
Since the student is on the 20-meter line, adding the horizontal distance to the starting position gives us:
Meter line the football lands on = 20 + 61.23 ≈ 81.23 meters
Therefore, the football lands on or around the 81.23-meter line.
3.Maximum height: The maximum height reached by the football can be found using the formula:
Maximum height = \(\frac{(initial velocity^2* sin^2(angle))}{ (2 * gravitational acceleration)}\)
Maximum height = \(\frac{(25^{2} * sin^2(53\°))}{(2 * 9.8)}\)
≈ 20.33 meters
To learn more about the time of flight from the given link
brainly.com/question/30337310
#SPJ4
Hi! I need the answer for this question: solve until you get the minimum expression: 2x . (x+y) + 1/5 x.x + 1/2 y . (x + 3)
Answers
Answer:
11/5 x^2 + 5/2 xy + 3/2 y.
Step-by-step explanation:
2x . (x+y) + 1/5 x.x + 1/2 y . (x + 3)
= 2x^2 + 2xy + 1/5 x^2 + 1/2xy + 3/2 y
= 11/5 x^2 + 5/2 xy + 3/2 y.