Select the expression that shows the value of the digits in the number below. (2 points) Four hundred and seventy-three thousandths 7 x 10 7 x one over ten 3 x one over one hundred 3 x one over one thousand Select the expression that shows the value of the digits in the number below. (2 points) Four hundred and seventy-three thousandths 7 x 10 7 x one over ten 3 x one over one hundred 3 x one over one thousand
Answers
Answer:
4 - Tenth
7 - Hundredth
3 - Thousandth
Step-by-step explanation:
The options are not clear.
However, the question is still solvable.
Given
Four hundred and seventy-three thousandths
Required
Determine the value of each digits
We start by representing as a number.
Represent this with x
x = Four hundred and seventy-three thousandths
\(x = \frac{473}{1000}\)
\(x = 0.473\)
The digits are: 4, 7 and 3
And they represent:
4 - Tenth
7 - Hundredth
3 - Thousandth
Answer:
D is the correct answer.
Step-by-step explanation:
3×1/1000 is the answer.
Related Questions
You have a balance of 17,426 on your credit card. Your minimum monthly payment is 461 . If your interest rate is 15.5%, how many years will it take to pay off your card assuming you don't add any debt? Enter your response to two decimal places (ex: 1.23)
Answers
With a credit card balance of $17,426, a minimum monthly payment of $461, and an interest rate of 15.5%, we need to calculate the number of years it will take to pay off the card without adding any additional debt.
To determine the time required to pay off the credit card, we consider the monthly payment and the interest rate. Each month, a portion of the payment goes towards reducing the balance, while the remaining balance accrues interest.
To calculate the time needed for repayment, we track the decreasing balance each month. First, we determine the interest accrued on the remaining balance by multiplying it by the monthly interest rate (15.5% divided by 12).
We continue making monthly payments until the remaining balance reaches zero. By dividing the initial balance by the monthly payment minus the portion allocated to interest, we obtain the number of months needed for repayment. Finally, we divide the result by 12 to convert it into years.
In this scenario, it will take approximately 3.81 years to pay off the credit card (17,426 / (461 - (17,426 * (15.5% / 12))) / 12).
Learn more about multiplying here:
https://brainly.com/question/30875464
#SPJ11
Suppose you draw two cards from a standard 52-card deck. Find the probability, when both cards are drawn without replacement, that the first card is a spade and the second card has a different suit. Give your answer as a fraction in its simplest form.

Answers
Given
First card to be drawn should be a spade
Second card drawn without replacement should be of different suit
Find
Probability, when both cards are drawn without replacement, that the first card is a spade and the second card has a different suit.
Explanation
Total cards = 52
Spades in a deck = 13
Probability of getting spades = 13/52
If the card drawn is not replaced then the cards will be 51
Probability of getting card from another suit = 39/51
Combined probabilty of both the
\(\begin{gathered} P=\frac{13}{52}\times\frac{39}{51} \\ \\ =\frac{13}{68} \end{gathered}\)Therefore probability of the event comes out to be 13/68 in simplest form
Final Answer
Probability of the event is 13/68
-5+(-4)
Adding and subtracting intergers
Answers
Answer:
9
Step-by-step explanation:
Integer
Consider this right triangle. R 9 55° Q P Enter the length of RQ, to the nearest tenth.
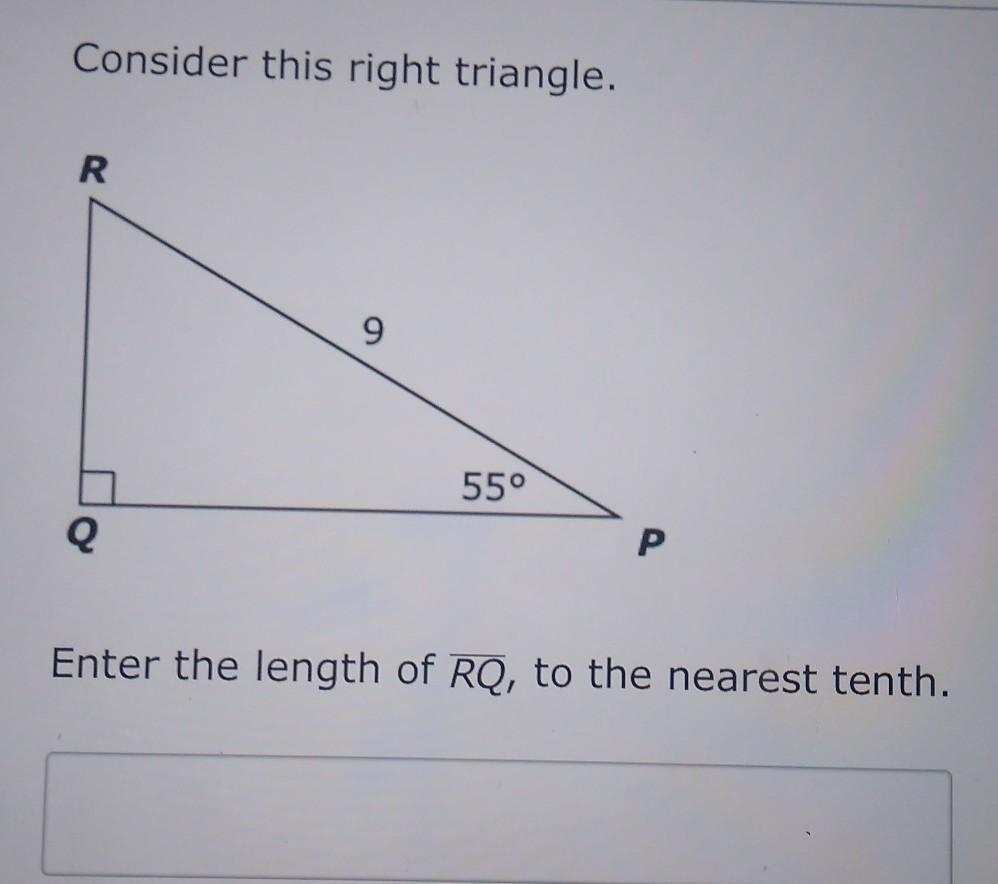
Answers
Answer:
RQ = 7.4
Step-by-step explanation:
From the right triangle PQR,
m∠Q = 90°
m∠P = 55°
Hypotenuse PR = 9
By applying sine rule in the given triangle,
Sin(55°) = \(\frac{\text{Opposite side}}{\text{Hypotenuse}}\)
0.819152 = \(\frac{\text{RQ}}{\text{PR}}\)
0.819152 = \(\frac{RQ}{9}\)
RQ = 9×0.819152
RQ = 7.37
≈ 7.4
prove that:cosA/sinA -sinA/cosA=2cos^2A-1/sinA cosA
Answers
Answer:
To prove that cosA/sinA -sinA/cosA=2cos^2A-1/sinA cosA, we can start by multiplying both sides of the equation by sinA cosA:
cosA/sinA -sinA/cosAsinA cosA = (2cos^2A-1)/sinA cosAsinA cosA
Now we can simplify the left side of the equation by using the identity sin^2A + cos^2A = 1:
cosAcosA -sinAsinA = (2cos^2A-1)cosAsinA
Now we can simplify the right side of the equation by using the identity cos^2A = 1 - sin^2A:
cosAcosA -sinAsinA = (2(1 - sin^2A)-1)cosAsinA
Finally, we can simplify the right side of the equation by using the identity sinAcosA = (sinAcosA)/(sinA*cosA):
cosAcosA -sinAsinA = (2(1 - sin^2A)-1)(sinAcosA)/(sinA*cosA)
Since both sides of the equation are equal, we can conclude that the statement is true.
find the minimum and maximum values of the function f(x, y) = x^2 y^2 subjevt to the given constraint x^4 y^4 = 8
Answers
Answer:
Step-by-step explanation:
We can use the method of Lagrange multipliers to find the extreme values of the function f(x,y) subject to the constraint x^4 y^4 = 8.
Let L(x, y, λ) = x^2 y^2 + λ(x^4 y^4 - 8) be the Lagrangian function.
Taking partial derivatives of L with respect to x, y, and λ, we get:
∂L/∂x = 2xy^2 + 4λx^3 y^4 = 0
∂L/∂y = 2x^2 y + 4λx^4 y^3 = 0
∂L/∂λ = x^4 y^4 - 8 = 0
From the first equation, we get x(2y^2 + 4λx^2 y^4) = 0. Since x cannot be zero (otherwise, the constraint would not hold), we have 2y^2 + 4λx^2 y^4 = 0, or y^2 = -2λx^2 y^4. Similarly, from the second equation, we have x^2 = -2λx^4 y^2.
Substituting y^2 = -2λx^2 y^4 into x^4 y^4 = 8, we get x^4 (-2λx^2 y^4)^2 = 8, or λ = -1/(2x^2 y^2).
Substituting λ into x^2 = -2λx^4 y^2, we get x^2 = 1/(2y^2), or y^2 = 1/(2x^2).
Substituting these values of x^2 and y^2 into the constraint x^4 y^4 = 8, we get 8 = 8/(4x^4), or x^4 = 1. Similarly, y^4 = 1.
Therefore, x = ±1 and y = ±1, and the critical points of f(x, y) subject to the constraint x^4 y^4 = 8 are (1,1), (1,-1), (-1,1), and (-1,-1).
To find the maximum and minimum values of f(x, y) subject to the constraint, we evaluate f(x, y) at each of these points:
f(1,1) = 1
f(1,-1) = 1
f(-1,1) = 1
f(-1,-1) = 1
Therefore, the minimum and maximum values of f(x, y) subject to the constraint x^4 y^4 = 8 are both equal to 1.
To solve this problem, we will use the method of Lagrange multipliers.
First, we define the Lagrangian function as L(x,y,λ) = x^2y^2 + λ(x^4y^4 - 8).
Next, we take partial derivatives of L with respect to x, y, and λ and set them equal to 0:
∂L/∂x = 2xy^2 + 4λx^3y^4 = 0
∂L/∂y = 2x^2y + 4λx^4y^3 = 0
∂L/∂λ = x^4y^4 - 8 = 0
Solving for λ in the third equation gives λ = 1/(4x^3y^3).
Substituting this into the first two equations and setting them equal to each other, we get:
2xy^2 + 4(1/(4x^3y^3))x^3y^4 = 2x^2y + 4(1/(4x^3y^3))x^4y^3
Simplifying and rearranging, we get:
x^3 = y^3
Substituting this into the constraint x^4y^4 = 8, we get:
x^4(x^3)^4 = 8
Solving for x, we get:
x = (2/√(3))^(1/7)
Substituting this back into x^3 = y^3, we get:
y = (2√3/3)^(1/7)
Finally, substituting these values of x and y back into the original function f(x,y) = x^2y^2, we get:
f(x,y) = (2/√(3))^(2/7) * (2√3/3)^(2/7) = 4/3^(3/7)
Therefore, the minimum and maximum values of the function f(x,y) subject to the given constraint are both 4/3^(3/7).
To find the minimum and maximum values of the function f(x, y) = x^2y^2 subject to the constraint x^4y^4 = 8, we can use the method of Lagrange multipliers.
Let g(x, y) = x^4y^4 - 8. The Lagrange multiplier method requires finding points where the gradients of f(x, y) and g(x, y) are proportional:
∇f(x, y) = λ ∇g(x, y)
Calculating the gradients, we get:
∇f(x, y) = (2x*y^2, 2x^2*y)
∇g(x, y) = (4x^3*y^4, 4x^4*y^3)
Now, equating the components and dividing:
(2x*y^2) / (4x^3*y^4) = (2x^2*y) / (4x^4*y^3)
Simplifying:
1 / (2x^2*y^2) = 1 / (2x^2*y^2)
Since this equality holds, the gradients are proportional. Now we use the constraint x^4y^4 = 8:
x^4y^4 = 8
To find the minimum and maximum, we'll analyze the possible critical points. If x = 0 or y = 0, then f(x, y) = 0. However, this would not satisfy the constraint, so we must have x ≠ 0 and y ≠ 0.
Take the fourth root of both sides of the constraint:
x*y = ±2
Now we have two cases:
Case 1: x*y = 2
f(x, y) = x^2y^2 = (xy)^2 = 2^2 = 4
Case 2: x*y = -2
f(x, y) = x^2y^2 = (xy)^2 = (-2)^2 = 4
Thus, the minimum value of f(x, y) is not found, as the constraint x^4y^4 = 8 doesn't allow for a minimum. The maximum value of f(x, y) is 4.
Learn more about Lagrange multipliers here: brainly.com/question/30776684
#SPJ11
can someone help me with this please? Thank you!

Answers
Answer:
528 cm²
Step-by-step explanation:
First I would calculate the area of the side rectangles:
20 x 9 = 180 cm²
There are two identical rectangles on both sides so i would x2
180 x 2 = 360 cm²
The area of the middle rectangle:
6 x 20 = 120 cm²
The area of the triangles:
Area of a triangle = (Base x Height)/2
8 x 6 = 48
48 ÷ 2 = 24
There are two identical triangles on the bottom and the top so x2
24 x 2 = 48
Now add all the values up:
360 + 120 + 48 = 528 cm²
I hope this helps!
Which is the most efficient step to solve the equation 2/3n=15 ?
Group of answer choices
Multiply both sides by 2/3
Subtract 15 from both sides
Subtract 2/3 from both sides
Divide both sides by 2/3
Answers
Answer:
This is the most optimal way to resolve the problem:
Step-by-step explanation:
15/n+2 = 3n/n
15/n+2 = 3
3 (n+2) = 15
n = 5 - 2
n = 3
1. what is the height of the cone? Explain how you found the height.
2. Now that you have the height of the cone, how can you solve for the slant height, s?
3. Now that you have the height of the cone, how can you solve for the slant height, s?

Answers
1. The height of the cone is equal to
2. You can solve for the slant height, s by applying Pythagorean's theorem.
3. To get from the base of the cone to the top of the hill, an ant has to crawl 29 mm.
How to calculate the volume of a cone?In Mathematics and Geometry, the volume of a cone can be calculated by using this formula:
Volume of cone, V = 1/3 × πr²h
Where:
V represent the volume of a cone.h represents the height.r represents the radius.By substituting the given parameters into the formula for the volume of a cone, we have the following;
8792 = 1/3 × 3.14 × 20² × h
26,376 = 3.14 × 400 × h
Height, h = 26,376/1,256
Height, h = 21 mm.
Question 2.
In order to solve for the slant height, s, we would have to apply Pythagorean's theorem since the height of the cone has been calculated above.
Question 3.
By applying Pythagorean's theorem, we have the following:
r² + h² = s²
20² + 21² = s²
400 + 441 = s²
s² = 841
Slant height, s = √841
Slant height, s = 29 mm.
Read more on cone here: https://brainly.com/question/27604827
#SPJ1
Pepper has 7.5 bags to clear 12 yd squared to distribute evenly among the beds . About how many bags will she need to use for each square yard?
Answers
Answer:
5/8 bags
Step-by-step explanation:
Pepper ha 7.5 bags
These bags are needed to clear 12 yards squared equally
Therefore the number of bags required for each square yard can be calculated as follows
= 7.5/12
= 0.625
0.625 to fraction is 5/8
Hence 5/8 bags is needed for each square yard
Explain why a + b = d.
B
A
C
swer

Answers
Answer:
Explanation below
Step-by-step explanation:
Angles in a Triangle
There are two basic relations of angles we need to recall:
Supplementary angles add up to 180°Internal angles of a triangle add up to 180°Note a, b, and c are the internal angles of the triangle. The angle c is what is needed to a+b to complete 180°, thus:
c = 180 - ( a + b )
Also, note c and d are supplementary angles. Again, c is what is needed to d to complete 180°, thus
c = 180 - d
From the two relations above, it follows that:
a + b = d
What is the term in mathematics for the operation or number that leaves others unchanged when combined with them? In multiplication, it is one, while in addition, it is zero?
Answers
The term is called an identity element. In multiplication, the identity element is one because any number multiplied by one results in the same number. In addition, the identity element is zero because any number added to zero results in the same number.
The term in mathematics for the operation or number that leaves others unchanged when combined with them is called the identity element.
It is also known by the name of neutral element.
In multiplication, the identity element is one (1) because when you multiply a number by one the result remains the same as the original number. For any number a,
a1=1a=a.
While in addition, the identity element is zero (0) because when you add zero to a number, the result remains the same as the original number. For any number a,
a+0=0+a=a.
There is no identity element for subtraction, and division only has an identity element for certain sets.
Know more about identity element here:
https://brainly.com/question/31372727
#SPJ11
May you please help me with this math sentence ?

Answers
In both the triangles,
three sides are congruent,
so,
the two triangles are related by side -side -side , so the triangles can be proven congruent .
How would your estimates have changed to get a more
accurate answer?
I know this question is vague but like, I don't want a full answer I just don't know where/how to start my explanation
Answers
Answer:
Im assuming you wrote a hypothesis or experimented or something, the "..." is where you write whatever your talking about I hope this helps :)
Step-by-step explanation:
My estimates would have changed to get a more accurate answer if I had previously known that.... would affect.... My estimate would have been...... because.....
What is the difference between
and ?
10
Answers
Answer:
ummmm
Step-by-step explanation:
HELP ME PLEASEEEEEEEE

Answers
Answer: Look in the attachment:
Step-by-step explanation: If it was random sampling, it would all be done randomly, barley without doing anything, and NOT doing anything particular, the 4 that are circled (in the attachment) are the ones that I am talking about; they ARE NOT examples of random sampling. If you look at the attachment, you might understand a little more :P

With what instrument could the predictive validity of a metric scale (a set of questions) best be determined?A. Cronbach's alphaB. A correlation-coefficient C. Fishers r-to-z test.D. With none of the above mentioned instruments
Answers
The best instrument to determine the predictive validity of a metric scale would be a correlation-coefficient.
This measure assesses the strength of the relationship between two variables, in this case, the metric scale scores and the predicted outcome. A high correlation would indicate that the metric scale is a good predictor of the outcome, whereas a low correlation would indicate that the metric scale is not a reliable predictor.
Cronbach's alpha is a measure of internal consistency and would not be appropriate for determining predictive validity. Fisher's r-to-z test is used to compare the strength of two correlations and is not necessary in this scenario. Therefore, the answer is B, a correlation-coefficient.
To learn more about Cronbach's alpha click here
brainly.com/question/30637862
#SPJ11
A star-patterned quilt has a star with the angles shown. What is the value of x? The diagram is not to scale.

Answers
Answer:
x = 81
Step-by-step explanation:
x + 24 = 105
Subtract 24 from both sides
x = 81
Simple.
The value of x is 81.
what is exterior angle property?If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
Given:
<1 = x
<2 = 24
exterior angle = 105
Now, using exterior angle property
105 = x +24
x= 105 - 24
x= 81
Hence, the value of x is 81
Learn more about exterior angle property here:
https://brainly.com/question/2406986
#SPJ5
What do the coordinates of an undefined slope have in common?
Answers
The coordinates of an undefined slope are points that are either the same or have no x-value. In both cases, the slope of a line between these points would be undefined because it would involve dividing by 0, which is not allowed in mathematics. This is because the slope of a line is calculated by dividing the difference in y-coordinates by the difference in x-coordinates, and if the x-coordinates are the same or do not exist, this division would result in an undefined value.
a farmer can exchange 72 pigs for 54 sheep at a price of 560 each. what is the price of 1 pig
Answers
Answer:
72*price of pig= 54*560
price of pig=54*560/72
= 420
Robert needs to score above 60 to pass Does anyone know the inequality help
Answers
Is this a function or not a function?
Image result for vertical line graph
Answers
Answer:
not a function. There cannot be mutiple y-values under one x value.
Step-by-step explanation:
CAN SOMEONE HELP I WILL GIVE BRAINLIST PLEASE!

Answers
Answer:
1) 24
2) 42
3) 26
4)44
Step-by-step explanation:
1) 2(8+4) = 2*12 = 24
2) 2(15+6) = 2*21 = 42
3) 2(4+9) = 2*13 = 26
4) 2(12+10) = 2*22 = 44
The base of a solid is a region in the first quadrant bounded by the x-axis, the y-axis, and he line x+2y=8. If the cross sections of the solid perpendicular to the x-axis are semicircles, what is the volume of the solid?
Answers
The volume of the solid is 16.75 unit³ in the given line x+2y=8 intercseting the x-axis, the y-axis.
What is volumes of Solids?
We shall encounter several solids and their corresponding volumes when discussing the concept of the volume of combination of solids. As is common knowledge, the surface areas and volumes of all three-dimensional shapes depend on their dimensions. As we can see in reality, numerous shapes are created by fusing a variety of shapes. For instance, the combination of a cone and cylinder shapes creates a tent. Similar to how a cone and a hemisphere combine to form an ice cream cone. As a result, the volume of the solids combined will equal the total of the volumes of the individual solids.
The line x+2y=8.
y = (8-x)/2
Volume will be V = π/2 ∫(r²) dr
So we have 1/3 π * r² * h
Here h = 8, r=2.
So V = 1/3 π * r² * h = 1/3 π * 2² * 8
V = 16.75 unit³
Hence,the volume of the solid is 16.75 unit³
Learn more about volumes of Solids, by the following link.
https://brainly.com/question/16717260
#SPJ4
help me please i don’t get it

Answers
Answer: Q=(9,5)
Step-by-step explanation: this is because 3 went to 6 and if you add 3 more it would be 9 and plus 3 and 4 so it would e five
Factor out the greatest common factor from the expression. \[ 9 a^{6}-27 a^{3} b^{3}+45 a^{5} b \]
Answers
The greatest common factor (GCF) of the expression 9a^6 - 27a^3b^3 + 45a^5b is 9a^3. Factoring out the GCF gives us 9a^3(a^3 - 3b^3 + 5ab).
To factor out the greatest common factor (GCF), we need to identify the largest common factor that can be divided evenly from each term of the expression.
Let's analyze each term individually:
Term 1: 9a^6
Term 2: -27a^3b^3
Term 3: 45a^5b
To find the GCF, we need to determine the highest exponent of a and b that can be divided evenly from all the terms. In this case, the GCF is 9a^3.
Now, let's factor out the GCF from each term:
Term 1: 9a^6 ÷ 9a^3 = a^3
Term 2: -27a^3b^3 ÷ 9a^3 = -3b^3
Term 3: 45a^5b ÷ 9a^3 = 5ab
Putting it all together, we have:
9a^6 - 27a^3b^3 + 45a^5b = 9a^3(a^3 - 3b^3 + 5ab)
Therefore, after factoring out the GCF, the expression becomes 9a^3(a^3 - 3b^3 + 5ab).
Learn more about highest exponent here:
brainly.com/question/30552488
#SPJ11
Can u help me understand how to write a function for the rule "the output is 3 less than 5 times the input" thanks :)
Answers
Answer:
I think it would be something like 5x - 3 =
If K = {(x, y ) | x - y = 5}, is Set K a function?
Answers
We can say that the set K is a function as it satisfies the definition of a function.
The answer is option B) Yes, K is a function. In summary, K = {(x, y) | x - y = 5} is a function because every element of the domain is related to exactly one element of the range.
Given K = {(x, y) | x - y = 5}. We need to determine whether the given set K is a function or not.
A function is a relation between two sets in which one element of the first set is related to only one element of the second set.
We can determine whether a given relation is a function or not by using the vertical line test.
In the given set K, for every value of x, there is a unique value of y such that x - y = 5. Hence, the set K can be represented as K = {(x, x - 5) | x ∈ R}.
Each element of the first set (domain) is related to exactly one element of the second set (range). In this case, for every value of x, there is a unique value of y such that x - y = 5.
Thus, we can conclude that the given set K is a function. Hence, the answer is option B) Yes, K is a function.
In summary, K = {(x, y) | x - y = 5} is a function because every element of the domain is related to exactly one element of the range.
For more such questions on function
https://brainly.com/question/29631554
#SPJ8
The doctor has written an order for 350 mg of a particular drug. It is only available in a
liquid form. If each mL of the liquid contains 25 mg of the drug, how much of the liquid
will need to be given? Use dimensional analysis to set up the problem.
Answers
Answer:
14 mL
Step-by-step explanation:
because 1 ml = 25 mg we just need to divide 350 mg by 25 mg to know how many mL are equivalent to 350 mg.
350/25 = 14
therefore 14mL is equivalent to the 350 mg of the drug.
Hence, the liquid will need to be given is \(14ml\) which is equivalent to the \(350\) mg of the drug.
What is an equation?
The definition of an equation is a mathematical statement that shows that two mathematical expressions are equal.
Here,
\(1ml=25mg\), here we need to divide \(350mg\) by \(25 mg\) to know how many \(ml\)are equivalent to \(350 mg.\)
i.e., \(\frac{350}{25}=14\)
Therefore, 14mL is equivalent to the \(350\) mg of the drug.
Hence, the liquid will need to be given is \(14ml\) which is equivalent to the \(350\) mg of the drug.
To know more about the equation
https://brainly.com/question/12788590
#SPJ2
Please help me I can’t figure it out

Answers
Answer:
20
Step-by-step explanation:
To evaluate the expression for a= 3, replace (or 'substitute') every 'a' you see with a '3' in the expression.
Given expression: 32 -4a
When a= 3,
32 -4a
= 32 -4(3)
= 32 -12
= 20
Answer:
20 is the value of expression when a is equal to 3 .Step-by-step explanation:
In the question we're given with an expression that is 32 - 4a , value of a is 3 . And we are asked to evaluate the expression for a = 3 .
Solution : -
\( \longmapsto \: 32 - 4a\)
Step 1 : Substituting value of a in given expression :
\( \longmapsto \:32 - 4(3)\)
Step 2 : Multiplying 4 with 3 :
\( \longmapsto \:32 - 12\)
Step 3 : Subtracting 12 from 32 :
\( \longmapsto \: \red{\boxed{ \frak{20}}}\)
Therefore , value of expression for 3 is 20 .#Keep Learning