PLEASE HELP WITH ATTACHED PHOTO:)
I completed the Venn diagram but a, b and c need answering, I don’t think the completed Venn diagram is completed right though. So please correct me if needed :)

Answers
Answer:
a. 0.69
b. 0.13
c.0.56
Step-by-step explanation:
Total number = 100
a) either means students with either option are valid
69/100 = 0.69
b) both means each student has done both math and english
=13/100 = 0.13
c) Only one means has done one subject and not both classes. We have 23 for math and 33 for english (this is according to your venn diagram)
23+33=56
one subject =56/100 = 0.56
Related Questions
Does anyone know this?

Answers
Answer:
42 cm²
Step-by-step explanation:
Length of the shaded rectangle = 7 cm
Width of the shaded rectangle= 7 - (0.5 + 0.5) = 7 - 1
Width of the shaded rectangle = 6 cm
Area of the shaded rectangle = L × W
Area = 7 × 6 = 42 cm²
A political researcher takes a survey of 300 randomly selected registered voters in atlanta, and each person was asked who they plan on voting for in the 2020 mayoral election. 101 said they plan on voting for candidate a, 184 said they plan on voting for candidate b, and 15 were unsure or plan to vote for another candidate. In question 8, the political researcher estimated p, the population proportion of all registered voters in atlanta who plan to vote for candidate a, with a 95% confidence interval. The researcher now wants to estimate p with a margin of error of 3%. What is the minimum sample size needed?.
Answers
The minimum sample size needed is 93.
Given:
A political researcher takes a survey of 300 randomly selected registered voters in atlanta, and each person was asked who they plan on voting for in the 2020 mayoral election. 101 said they plan on voting for candidate a, 184 said they plan on voting for candidate b, and 15 were unsure or plan to vote for another candidate. In question 8, the political researcher estimated p, the population proportion of all registered voters in atlanta who plan to vote for candidate a, with a 95% confidence interval. The researcher now wants to estimate p with a margin of error of 3%.
here
n = 101
p = 0.5
e = 5%=0.05
z score at 95% = 1.96
\(n'=\frac{n}{1+\frac{z^2*p(1-p)}{e^2} }\)
On submitting and solving using calculator
n = 93
Learn more about the sample size here:
https://brainly.com/question/28044641
#SPJ1
Here is a list of numbers:
-5, -15, -10, 5, 14, 5, -18, 11, -4
State the median.
Answers
Answer:
4
Step-by-step explanation:
-18, -15, -10, -5, 4, 5, 5, 11, 14
There are 9 terms. So the one in the middle is the median.
-18, -15, -10, -5, 4, 5, 5, 11, 14
1 2 3 4 5 6 7 8 9
So 4 is the median.
---
hope it helps
Your friend says that the quotient 3/8 divided by 1/8 is 1/3 what is the correct quotient? What mistake did you friend likely make?

Answers
Answer:
its 1/8
Step-by-step explanation:
he said 1/3 it does not match the other 2 numbers hope its right ;-; also helpfull
Ok i want the answer if someonr knows it please help me

Answers
\(\huge \text{Hello there! :)}\)
I'm Joyous to help you today!
Answer:
\(3h=54\)
Step-by-step explanation:
To get the product between 3 and Han's score (h), we multiply them:
\(3~x~h~--> 3h\)
And since we know that this product is equal to 54, we'll have that the equation that corresponds to the situation is:
\(3h=54\)
Hope this Helps!
Thanks for choosing Brainly!
Ozzie's Mother bought an assortment of greeting cards while she was at the bookstore. She bought twice as many birthday cards as anniversary cards. She bought 2 fewer anniversary cards than general greetings cards, but 2 more anniversary cards than get well cards. If she bought 2 get well cards, how many cards did she buy in all?
Brainlist
Answers
Answer:
20
Step-by-step explanation:
2 get well cards
4 anniversary cards
6 greeting cards
8 birthday cards
please hand solve and show steps
(a) Find the dual of the LP .
(b) Find the standard form of the LP and dual.
(c)Optimal solution for the primal problem is: x ∗ 1 = 20, x∗ 2
= 60, s∗ 1 = 0, s∗
objective m constraints n decision variables Consider the following LP. Primal and Dual pair min b₁y₁+ max C₁x₁++GX+ CnXn 8/1X1 +2X2 + + ax ≤ bi ax1 + a2x2 + +anxn bi a/1X1 + a2x2 + +anxn 2
Answers
(a) Find the dual of the LP.Primal problem isminimize \($b_1y_1+C_1x_1+...+C_nx_n$\) subject to \($a_{11}x_1+a_{12}x_2+...+a_{1n}x_n \leq\) \(b_1$...$a_{m1}x_1+a_{m2}x_2+...+a_{mn}x_n \leq b_m$ and $x_1, x_2,\)..., x_n\(\geq 0$\)
Let us find the dual of the above primal problem.
Dual problem ismaximize \($b_1y_1+...+b_my_m$\)subject to \($a_{11}y_1+a_{21}y_2+...+a_{m1}y_m \leq\)\(C_1$...$a_{1n}y_1+a_{2n}y_2+...+a_{mn}y_m \leq C_n$\)
and\($y_1, y_2, ..., y_m \geq 0$\)
(b) Find the standard form of the LP and dual.Standard form of the primal problem isminimize \($b_1y_1+C_1x_1+...+C_nx_n$\)subject to \($a_{11}x_1+a_{12}x_2+...+a_{1n}x_n +s_1 = b_1$...$a_{m1}x_1+a_{m2}x_2+...+a_{mn}x_n +s_m = b_m$\) and\($x_1, x_2, ..., x_n, s_1, s_2, ..., s_m \geq 0$\)
Standard form of the dual problem ismaximize \($b_1y_1+...+b_my_m$\)subject to \($a_{11}y_1+a_{21}y_2+...+a_{m1}y_m \leq 0$...$a_{1n}y\)
To know more about isminimize visit:
https://brainly.com/question/32370699
#SPJ11
Write an arithmetic sequence for each formula.

Answers
The elements of the arithmetic sequences of the first part are:
n = 0: - 6, n = 1: 11, n = 2: 28, n = 3: 45, n = 4: 62n = 1: 15, n = 2: 10, n = 3: 5, n = 4: 0, n = 5: - 5n = 1: 15, n = 2: 10, n = 3: 5, n = 4: 0, n = 5: - 5n = 0: 10, n = 1: 14, n = 2: 18, n = 3: 22, n = 4: 26n = 0: - 43, n = 1: - 22, n = 2: - 1, n = 3: 20, n = 4: 41n = 0: 24, n = 1: 30, n = 2: 36, n = 3: 42, n = 4: 48The general terms of the arithmetic sequences of the second part are:
y = 78 + 72 · n, n ≥ 0.y = 18 + 7 · n, n ≥ 0.y = - 14 - 16 · n, n ≥ 0.y = 5 + 3 · n, n ≥ 0.How to analyze arithmetic sequences
Arithmethic sequences are sequences whose elements are generated linear equations of the form:
y = a + b · n, n ≥ 0 (1)
Where:
a - Value of the first element of the sequence.b - Difference between any pair of consecutive elements.x - Index of the element.
In the first part we need to calculate the first five elements for six sequences:
The second part consists in finding the general term of the arithmetic sequence, that is, looking for the formula that generates all elements:
a = 78, b = 72, y = 78 + 72 · n, n ≥ 0.a = 18, b = 7, y = 18 + 7 · n, n ≥ 0.a = - 14, b = - 16, y = - 14 - 16 · n, n ≥ 0.a = 5, b = 3, y = 5 + 3 · n, n ≥ 0.To learn more on arithmetic sequences: https://brainly.com/question/10396151
#SPJ1
Construct a truth table for each of these compound propositions
a) p → ⇁p
b) p ↔ ⇁p
c) p ⊕ (p V q) d) (p ∧ q) → (p V q) e) (p → ⇁p) ↔ (p ↔ q) f) (p ↔ q) ⊕ (p ↔ ⇁q)
Answers
After considering the given data we conclude that there truth table is possible and is placed in the given figures concerning every sub question.
A truth table is a overview that projects the truth-value of one or more compound propositions for each possible combination of truth-values of the propositions starting up the compound ones.
Every row of the table represents a possible combination of truth-values for the component propositions of the compound, and the count of rows is described by the range of possible combinations.
For instance, if the compound has just two component propositions, it comprises four possibilities and then four rows to the table. The truth-value of the compound is projected on each row comprising the truth functional operator.
To learn more about truth table
https://brainly.com/question/28605215
#SPJ4



A number is st least -2
Answers
Answer:
-3
Step-by-step explanation:
the distance betwee
4. C(0,0), D(5,2)
Answers
Answer:
\( \sqrt{29} \)
Step-by-step explanation:
Distance between C and D=
under root[(5-0)^2+(2-0)^2]
=under root(25+4)
=under root29
Can a triangle be formed with side lengths of 8 cm, 9 cm, and 17 cm? __________ Answer, yes or no, in the blank. (5 points)
Answers
Answer:
yes
Step-by-step explanation:
Evaluate x(–y + z) for x = –1, y = 2, and z = 5.
7
3
–3
–7
Answers
Answer:
-3
Step-by-step explanation:
-1(-2+5)
-1 multiplied by (-2+5)
+2-5
=-3
Hope this helped!
Answer:-3
Step-by-step explanation:
9: Find sinθ if cosθ=4/5 is in the first quadrant.
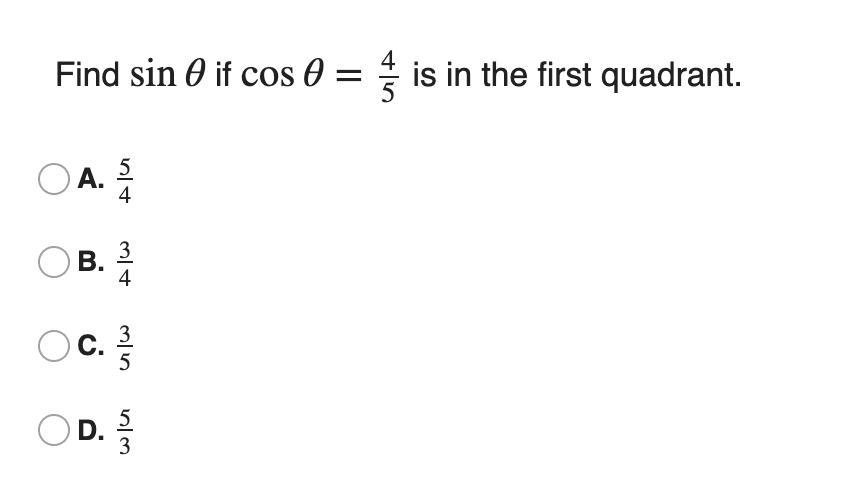
Answers
Answer: We have to find the sin(theta) provided the cos(theta) function, the visualization of the problem is as follows:
\(cos(\theta)=\frac{4}{5}\)The diagram visualization is:
Therefore the x is:
\(x=\sqrt{5^2-4^2}=3\)Therefore the answer is:
\(sin(\theta)=\frac{3}{5}\)The answer is Option(C).

Write an equation of a hyperbola with the given foci and vertices.
foci (0, ± 13) , vertices (0, ±5)
Answers
The final equation of the hyperbola is:
x² / 25 - y² / 144 = 1
The equation of the hyperbola with foci at (0, ±13) and vertices at (0, ±5) can be written in the form:
(x - h)² / a² - (y - k)² / b² = 1
Where (h, k) represents the center of the hyperbola. In this case, the center is at (0, 0) since the foci and vertices are symmetric about the origin.
Using the distance formula, we can determine the values of 'a' and 'b'. The distance between the center and each focus is equal to 'c', and the distance between the center and each vertex is equal to 'a'. In this case, 'c' is 13 and 'a' is 5.
Therefore, the equation of the hyperbola is:
x² / 25 - y² / b² = 1
To find the value of 'b', we can use the relationship between 'a', 'b', and 'c' in a hyperbola. The relationship is given by:
c² = a² + b²
Substituting the known values, we have:
13² = 5² + b²
169 = 25 + b²
b² = 144
b = 12
So, the final equation of the hyperbola is:
x² / 25 - y² / 144 = 1
This equation represents a hyperbola with foci at (0, ±13) and vertices at (0, ±5), centered at the origin (0, 0). The term 'a' represents the distance between the center and the vertices, and 'b' represents the distance between the center and the asymptotes of the hyperbola.
Learn more about hyperbola here:
https://brainly.com/question/19989302
#SPJ11
CD has endpoints C(-3, 4) and D(1, -2). Find the coordinates
of its midpoint.
Answers
Answer:
Midpoint (-1 , 1)
Step-by-step explanation:
Formula: (midpoint)
Let the point A(x , y) be the midpoint of CD.
\(x=\frac{x_c+x_D}{2} =\frac{-3+1}{2} =\frac{-2}{2} =-1\)
\(y=\frac{x_C + y_D}{2} =\frac{4+(-2)}{2} =\frac{2}{2} =1\)
Then
A(-1 , 1)

Answer: (-1;1)
Step-by-step explanation:
x =(-3+1)/2
Y=(4-2)/2
The taxi charges $3 just for the pickup and then an additional $1.75 per mile driven. How much would a taxi ride cost if Stella is riding for 2 miles? How much would a taxi ride cost that is mm miles long?
Answers
Answer:
Step-by-step explanation:
It’s your mom
the patient recovery time from a particular surgical procedure is normally distributed with a mean of 5.2 days and a standard deviation of 2.3 days. what is the probability of spending more than 2 days in recovery? (round your answer to four decimal places.)
Answers
When the patient recovery time from a specific surgical procedure is normally distributed, with a mean of 5.2 days and a standard deviation of 2.3 days, the probability of spending more than 2 days in recovery will be 0.61.
What is probability?Simply put, probability is the likelihood that something will occur. When we don't know how an event will turn out, we can discuss the likelihood or likelihood of various outcomes. Statistics is the study of events that follow a probability distribution. Information about the likelihood that something will happen is provided by probability. For instance, meteorologists use weather patterns to forecast the likelihood of rain. Probability theory is used in epidemiology to comprehend the connection between exposures and the risk of health effects.
Here,
z=(X-μ)/σ
X=2
μ=5.2
σ=2.3
Z=(2-5.2)/2.3
Z=-1.39
-1.39+1
=0.39
1-0.39=0.61
The probability of spending more than 2 days in recovery will be 0.61 when the patient recovery time from a particular surgical procedure is normally distributed with a mean of 5.2 days and a standard deviation of 2.3 days.
To know more about probability,
https://brainly.com/question/11234923?referrer=searchResults
#SPJ4
Let n be odd, let a be even, and let : {1, ..., n} + {1,..., n} be a permutation. Prove that the product (a +1 – 7(1))(a + 2 – 7(2)) ... (a +n – 7(n)) is even. Is the same conclusion necessarily true if n is even or if a is odd? Give a proof or a counterexamples in each case.
Answers
The product is even when there are equal number of odd and even numbers. The conclusion is also true when n is even or a is odd. The product is even when there are equal number of odd and even numbers. Now, let's see if the same conclusion is true if n is even or a is odd.
Given: Let n be odd, let a be even, and let : {1, ..., n} + {1,..., n} be a permutation.
To prove: The product (a +1 – 7(1))(a + 2 – 7(2)) ... (a +n – 7(n)) is even.
Proof: Given, {1, ..., n} + {1,..., n} is a permutation.
This means that every number is repeated exactly once. Hence, there are n even numbers and n odd numbers.
So, among the n numbers, there are equal even and odd numbers. Now, we can break down each term of the product as follows:
a + k – 7k = a – 6k
So, each term is an even number as a is even and 6k is even as k is an integer. Now, we have n terms in the product. Out of these n terms, equal number of terms are even and odd. If we multiply an even number with an odd number, the product is even, i.e.,
even × odd = even.
Hence, the product is even when there are equal number of odd and even numbers. Now, let's see if the same conclusion is true if n is even or a is odd.
Case 1: If n is even
Let's consider n = 2. Here, there are equal number of even and odd numbers (1 and 2) among the two numbers.
So, the product is given as (a – 6)(a – 12)
When a = 7, the product is 0, which is even.
So, the conclusion is true when n is even.
Case 2: If a is odd
Let's consider n = 3. Here, there are more odd numbers than even numbers (1, 2, and 3).
So, the product is given as (a – 6)(a – 12)(a – 18)
When a = 1, the product is 10, which is even.
So, the conclusion is also true when a is odd. The product (a +1 – 7(1))(a + 2 – 7(2)) ... (a +n – 7(n)) is even. It is given that n is odd and a is even.
Also, {1, ..., n} + {1,..., n} is a permutation which means that every number is repeated exactly once.
Hence, there are n even numbers and n odd numbers. So, among the n numbers, there are equal even and odd numbers. Now, we can break down each term of the product as follows:
a + k – 7k = a – 6k.
So, each term is an even number as a is even and 6k is even as k is an integer.
Now, we have n terms in the product. Out of these n terms, equal number of terms are even and odd. If we multiply an even number with an odd number, the product is even, i.e.,
even × odd = even.
Hence, the product is even when there are equal number of odd and even numbers. The conclusion is also true when n is even or a is odd.
To know more about permutation visit: https://brainly.com/question/32683496
#SPJ11
What is the grade of the road shown below expressed as a percent rounded to one decimal place?
Rise is 40feet
Run is 380 feet
Answers
The grade of the road with given rise of 400 feet and run of 380 feet is equal to 10.5% approximately when rounded to one decimal place.
Rise is equal to 40feet
Run is equal to 380 feet
To find the grade of the road, we can use the formula,
Grade = (Rise / Run) × 100
As the rise is 40 feet and the run is 380 feet, we can substitute these values into the formula we have,
Grade = (40 / 380) × 100
Calculating this expression we get,
⇒ Grade = 0.10526315789473684 × 100
⇒ Grade ≈ 10.5
Therefore, the grade of the road is approximately 10.5% when rounded to one decimal place.
learn more about decimal place here
brainly.com/question/31046435
#SPJ4
If u=⟨3,0,5⟩ and v=⟨−3,4,−5⟩, then the component of u along v is
Answers
The component of u along v is -17√2 / 5. To find the component of u along v, we can use the formula Component of u along v = (u · v) / |v| where u · v represents the dot product of u and v, and |v| represents the magnitude of v.
Given u = ⟨3, 0, 5⟩ and v = ⟨-3, 4, -5⟩, we can calculate their dot product:
u · v = (3 * -3) + (0 * 4) + (5 * -5) = -9 - 25 = -34
Next, we need to find the magnitude of v:
|v| = √((-3)^2 + 4^2 + (-5)^2) = √(9 + 16 + 25) = √50 = 5√2
Now, we can substitute these values into the formula to find the component of u along v:
Component of u along v = (-34) / (5√2)
To simplify, we can rationalize the denominator by multiplying both the numerator and denominator by √2:
Component of u along v = (-34√2) / (5√2 * √2)
= (-34√2) / (5 * 2)
= -17√2 / 5
Therefore, the component of u along v is -17√2 / 5.
Learn more about denominator here:
https://brainly.com/question/32621096
#SPJ11
A grocery store sells a bag of 3 oranges for $1.23. If Latanya spent $3.28 on oranges, how many did she buy?
Answers
Answer: 8 Oranges
Step-by-step explanation:
Given information
3 Oranges = $1.23
Total cost = $3.28
Determine the unit price of an orange
Unit price = Cost ÷ Number of Oranges
Unit price = 1.23 ÷ 3
Unit price = $0.41 / orange
Determine the number of oranges bought
Number of orange × Unit price = Total cost
N × (0.41) = (3.28)
Divide 0.41 on both sides
N = 3.28 ÷ 0.41
\(\Large\boxed{Number~of~oranges=8}\)
Hope this helps!! :)
Please let me know if you have any questions
Is inverse relationship direct?
Answers
An inverse relationship can not direct.
We know that an inverse proportion represents inverse or indirect relation between two quantities.
In inverse relationship, one value increases while the other value decreases, and vice versa.
But in case of direct relationship, if one quantity increases , the other quantity also increases, and if one quantity decreases , the other quantity also decreases.
When two quantities 'm' and 'n' are inversely proportional to each other, it means when the value of m increases while the value of quantity 'n' decreases, and vice versa.
Also, an inverse relationship always has a negative slope.
Learn more about inverse proportional relations here:
brainly.com/question/1266676
#SPJ4
Erin has $50. She wants to purchase a cell phone ($20) and spend the rest on music CDs. Each music CD costs $8. Write an inequality for the number of music CDs she can purchase.
HELP ME PLSS ANSWER QUICKLY,
(If you can give me the complete answer I would really appreciate it :) )
Answers
Answer:
Step-by-step explanation:
$50-$20=$30
$30/8= 3.75
since you cannot but 3/4 of a CD you have to round down to 3 to she can buy the phone and 3 CDs and have $6 left over
HELP if a person runs 5 miles in 25 minute, how long will it take them to run 8 miles at the same rate?
Answers
Answer:1.6
Step-by-step explanation:
25/5=5
8/5=1.6
Answer:
40 MinutesStep-by-step explanation:
if 5miles = 25 minutes
then, 8 miles = X
hence X minutes
\(x = \frac{25minutes}{5miles} \times 8miles\)
X=40 minutesPLEASE HELP URGENT WITH 4 AND 6

Answers
The solution is
a) The compound interest for the second period is $ 2.01 and the amount after the second period is $ 404.01
b) The compound interest for the first period is $ 114.125 and the amount is $ 18,374.125
The compound interest for the second period is $ 114.83828125 and the amount after second period is $ 18,488.96
What is Compound Interest?
Compound interest is interest based on the initial principle plus all prior periods' accumulated interest. The power of compound interest is the ability to generate "interest on interest." Interest can be added at any time, from continuously to daily to annually.
The formula for calculating Compound Interest is
A = P ( 1 + r/n )ⁿᵇ
where A = Final Amount
P = Principal
r = rate of interest
n = number of times interest is applied
b = number of time periods elapsed
Given data ,
a)
Let the principal be P = amount after first period = $ 402
Now , the rate of interest r = 6 %
The compound interest is calculated by compounding monthly
Now , the interest for the second period = ( PRT / 100 x 12 )
Substituting the values in the equation , we get
The interest for the second period = ( 402 x 6 x 1 ) / 1200
The interest for the second period = $ 2.01
The amount after the second period = amount after first period + interest for the second period
The amount after the second period = 402 + 2.01
The amount after the second period = $ 404.01
b)
Let the principal be P = $ 18260
The rate of interest r = 2.5 %
The compound interest is calculated by compounding quarterly
Now , the interest for the first period = ( PRT / 4 x 100 )
Substituting the values in the equation , we get
The interest for the first period = ( 18260 x 2.5 ) / 400
The interest for the first period = 45650 / 400
The interest for the first period = $ 114.125
The amount for the first period = 18260 + 114.125
The amount for the first period = $ 18,374.125
Now , the principal for the second period = interest + amount of first period
The principal for the second period = $ 18,374.125
The rate of interest = 2.5 %
The interest for the second period = ( PRT / 4 x 100 )
Substituting the values in the equation , we get
The interest for the second period = ( 18374.125 x 2.5 ) / 400
The interest for the second period = 45935.3125 / 400
The interest for the second period = $ 114.83828125
The amount for the second period = 18,374.125+ 114.84
The amount for the second period = $ 18,488.96
Hence , the amount and interest is calculated
To learn more about compound interest click :
https://brainly.com/question/21270833
#SPJ1
Help me with this Question Please.

Answers
Answer:
\(3 \times \frac{1}{3 } + \frac{1}{2} \times - 12( \frac{1}{3} ) = \frac{1}{3} \)
A recipe calls for 33 pounds of pasta to serve 1414 people. Of a restaurant is cooking pasta for a party of 5656 people, what should they do
Answers
Answer:
the restaurant should cook 132 pounds of pasta for the party of 5656 people.
Step-by-step explanation:
If a recipe calls for 33 pounds of pasta to serve 1414 people, then the amount of pasta needed to serve 5656 people can be calculated using the following proportion:
33 pounds / 1414 people = x pounds / 5656 people
Solving for x gives:
x = (33 * 5656) / 1414 = 132 pounds
Therefore, the restaurant should cook 132 pounds of pasta for the party of 5656 people. I hope this helps!
The measure of a diagonal of a square is represented by the expression 4x – 10. If the measure of the other diagonal is 10 meters, what is the value of x?
Answers
If the measure of a diagonal of a square is 4x – 10 and the other diagonal is 10 meters, then the value of x is 5.
In a square, the two diagonals are equal in length and bisect each other at a 90-degree angle. The diagonals of a square divide the square into four congruent right triangles.
Additionally, the diagonals of a square are also perpendicular bisectors of each other. This means that if you draw a line connecting the midpoints of the two diagonals, this line will be perpendicular to both diagonals and will divide each diagonal into two congruent segments.
To find the value of x, equate the expression for the diagonal with the length of the other diagonal.
4x – 10 = 10
Isolate x in one side.
4x = 20
Divide both sides by 4.
x = 5
Hence, the value of x is equal to 5 meters.
Learn more about diagonal of a square here: https://brainly.com/question/11232704
#SPJ4
X=
2x 10,
4
10
How do i find x?

Answers
Answer:Solve for x 2x-4=10 2x − 4 = 10 2 x - 4 = 10 Move all terms not containing x x to the right side of the equation. Tap for more steps... 2x = 14 2 x = 14 Divide each term in
Step-by-step explanation: