Answers
Answer:
B
Step-by-step explanation:
Related Questions
Investment question Part 2: $3,500 is invested at 7%. How much money
will be in the account after 17 years?
Answers
Answer:
$7665
Explanation:
simple interest: principal * rate (%) * time (years)
Given:
principal: $3,500
rate: 7%
time: 17 years
Solve for interest received:
3,500 * 7% * 17
$4165
Total money in account:
$4165 + $3,500
$7665
If an explanatory variable is exogenous it implies that: a. the variable cannot be correlated with other explanatory variables. b. the variable is not correlated with the regression error. c. the variable must have zero mean. d. the value of the variable must be randomly assigned.
Answers
b. the variable is not correlated with the regression error. if an explanatory variable is exogenous, it means that the variable is not correlated with the regression error term. This assumption is important for obtaining unbiased and consistent parameter estimates in regression analysis.
If an explanatory variable is exogenous, it implies that the variable is not correlated with the regression error term. In other words, the exogenous variable is unrelated to the factors that are not explicitly included in the regression model and captured by the error term.
Exogeneity is an important assumption in regression analysis, as violating this assumption can lead to biased and inconsistent parameter estimates. When an explanatory variable is exogenous, it means that its value is determined independently of the other variables in the model and the error term.
Let's briefly discuss the other options:
a. The variable cannot be correlated with other explanatory variables: Exogeneity does not necessarily imply that the variable cannot be correlated with other explanatory variables. Explanatory variables can be correlated with each other as long as they are not correlated with the regression error term.
c. The variable must have zero mean: Exogeneity does not require that the variable has a zero mean. Exogeneity refers to the lack of correlation between the variable and the regression error, not its mean value.
d. The value of the variable must be randomly assigned: Exogeneity does not require that the value of the variable is randomly assigned. Exogeneity implies that the variable is not affected by the regression error and is determined independently of the other variables in the model, but it does not necessarily imply a random assignment of values.
In summary, if an explanatory variable is exogenous, it means that the variable is not correlated with the regression error term. This assumption is important for obtaining unbiased and consistent parameter estimates in regression analysis.
Learn more about variable here
https://brainly.com/question/28248724
#SPJ11
PLZ HELP ME!!!!! IF ANSWER IS CORRECT, I WILL GIVE U BRAINLIEST

Answers
Answer:
\( 2.58 \times {10}^{8} \)
Step-by-step explanation:
\(9.3. {10}^{7} - 3.4. {10}^{6} \\ = (27 \times 10 - 12) \times {10}^{6}\\ = (270 - 12) \times {10}^{6} \\ = 258 \times {10}^{6} \\ = 2.58 \times {10}^{6 + 2} \\ = 2.58 \times {10}^{8} \)
Answer: i don't know
Step-by-step explanation:
what is this
also i need points! sry
Please help ill appreciate it

Answers
Answer:
B
Step-by-step explanation:
the area of the triangle is 18 square units
WRAP-UP Menu Subtracting Fractions . please help

Answers
Answer:
5/24 more
Step-by-step explanation:
1/3 turns into 8/24
and
1/8 turns into 3/24
so eric has read 5/24 more
Answer:
5/24
Step-by-step explanation:
1/8×3=3/24
1/3×8=8/24
8/24-3/24=5/24.
At Imelda's fruit stand, you bought 555 apples and 444 oranges for \$10$10dollar sign, 10, and your friend bought 555 apples and 555 oranges for \$11$11dollar sign, 11. Using this information, is it possible to determine the cost of one apple and one orange from the fruit stand? If so, what do they cost? If not, why not? Choose 1 answer:
Answers
Answer:
Each apple would cost 1.20 and each orange would cost 1
Step-by-step explanation:
Answer:
See Attached!
Step-by-step explanation:
Determine whether the given value is a statistic or a parameter. After taking the firstexam, 15 of the students dropped the class:1-Parameter?2-Statistic?
Answers
Given: After taking the first exam, 15 of the students dropped the class.
Required: To determine whether the given value is a statistic or a parameter.
Explanation: Parameter and statistic are very similar. The parameter is when the complete data of the population is presented. The statistic is when a particular data is used for fraction of the population.
Since it is given that among all the students in the class 15 students dropped out. Hence the given data is Parameter.
Final Answer: Parameter.
Gym A has an membership
fee of $100 and a monthly
cost of $30. Gym B has a
membership fee of $70 and a
monthly cost of $40. How
many months until both cost
the same?
Answers
Answer: 3months
Step-by-step explanation:
130 160 190 220 250 280 310 340 370 400
110 150 190 230 270 310 350 390 430 470 510
After 3 months they will both be at 190
Answer:
3 months until both costs are the same
Step-by-step explanation:
30x+100 = 40x+70
-30 -30
100 = 10x+70
-70 -70
30 = 10x
30/10 10x/10
30/10 = 3
b) The monthly income of A is double than that of B and the monthly income of B is treble than that of C. If the total income of three persons is Rs 80,000, find monthly income of each of person.
Answers
Answer:
A = Rs 48,000
B = Rs 24,000
C = R2 8,000
Step-by-step explanation:
To solve this problem, create and solve a system of linear equations using the given information.
From the given information:
If the monthly income of A is double than that of B, then A = 2B.If the monthly income of B is treble than that of C, then B = 3C.If the total income of three persons is Rs 80,000, then A + B + C = 80000.Therefore, the system of linear equations is:
\(\begin{cases}A=2B\\B=3C\\A+B+C=80000\end{cases}\)
Substitute the second equation into the first to create and equation for A in terms of C:
\(\begin{aligned}A &= 2B\\&=2(3C)\\&=6C\end{aligned}\)
Substitute this and the second equation into the third equation and solve for C:
\(\begin{aligned}A+B+C&=80000\\6C+3C+C&=80000\\10C&=80000\\C&=8000\end{aligned}\)
Now that we have found the monthly income of person C, substitute this value into the expressions for A and B to calculate the monthly incomes of persons A and B:
\(\begin{aligned}A &=6C\\&=6(8000)\\&=48000\end{aligned}\)
\(\begin{aligned}B &=3C\\&=3(8000)\\&=24000\end{aligned}\)
Therefore, the monthly income of each person is:
A = Rs 48,000B = Rs 24,000C = R2 8,000What is 6 2/5+7 9/10? Simplify your answer and explain your answer.
Answers
Answer:
13 3/10
Step-by-step explanation:
first you add the whole numbers, that equals 13
now make the denominators the same by multiplying or dividing the numerator and denominator to an equivalent fraction, I divided 2/5 to 4/10
now you add the numerators and you have 13 13/10
make that a proper fraction and you have 14 3/10
Answer:
14.3
Step-by-step explanation:
(6 2/5) + (7 9/10)= 14.3
changes in free energy (g) are related to both enthalpy and entropy. which equation best represents this?
Answers
The total amount of energy released or absorbed by the reaction, which is the change in free energy.
ΔG = ΔH - TΔS
This equation, also known as the Gibbs Free Energy equation, is used to calculate the change in free energy (ΔG) resulting from a chemical reaction. The equation states that the change in free energy is equal to the change in enthalpy (ΔH) minus the product of the absolute temperature (T) and the change in entropy (ΔS).
The enthalpy change (ΔH) is the change in the amount of energy released or absorbed during a reaction at constant pressure. It is a measure of the amount of energy stored in the bonds of the reactants and products. The entropy change (ΔS) is the measure of the randomness or disorder of a system. It is a measure of how much energy is dispersed or spread out from the reaction.
By combining the enthalpy and entropy changes of a reaction, the Gibbs Free Energy equation can be used to calculate the total amount of energy released or absorbed by the reaction, which is the change in free energy. For example, if ΔH is -50 kJ and ΔS is +40J/K, then the change in free energy is -10 kJ.
Learn more about equation here:
https://brainly.com/question/10413253
#SPJ4
Cup holds 8 oz and a glass holds 6 oz. Calculate the total intake (mL) for the patient: 1/2 cup of orange juice, 2/3 glass of milk, full cup of lemonade, full glass of water, 1 popsicle (3 ounces) and 4 ounces ice chips.
Answers
According to the given measurement, the total amount of intake is 621.0435 ml
Here we have given the following measurements they are listed as follows:
=> 1/2 cup of orange juice,
=> 2/3 glass of milk, full cup of lemonade,
=> full glass of water,
=> 1 popsicle (3 ounces) and
=> 4 ounces ice chips.
Here we also know that
1 cup = 8 oz
1 glass = 6 oz
And as per the Si measurements,
1 oz = 29.5735 ml.
To order to calculate the total amount of intake we have to sum all the given measurements, then we get,
=> 1/2(8) + 2/3(6) + 6 + 3 + 4
When we simplify this one then we get,
=> 4 + 4 + 6 + 3 + 4 = 21
Now, we have to convert ounce into milliliter, for that we have multiply 29.5735 with the total measurement, then we get,
=> 21 x 29.5735 = 621.0435 ml
To know more about total here.
https://brainly.com/question/14286201
#SPJ4
Riverboat Adventures pays $310,000 plus $15,000 in closing costs to purchase real estate. The real estate consists of land appraised at $35,000, a building appraised at $105,000, and land improvements appraised at $210,000. Compute the cost that should be allocated to the land.
Answers
To determine the cost allocated to the land, we need to calculate the proportionate cost of the land in relation to the total appraised value of the real estate. Therefore, the cost allocated to the land is $32,500.
The total cost paid for the real estate is $310,000 plus $15,000 in closing costs, totaling $325,000. To allocate the cost to the land, we need to calculate the proportion of the land's appraised value to the total appraised value of the real estate.
The total appraised value of the real estate is the sum of the appraised values of the land, building, and land improvements, which amounts to $35,000 + $105,000 + $210,000 = $350,000.
To calculate the cost allocated to the land, we divide the appraised value of the land by the total appraised value of the real estate and multiply it by the total cost paid:
Cost allocated to land = (Appraised value of land / Total appraised value) * Total cost
= ($35,000 / $350,000) * $325,000
= 0.1 * $325,000
= $32,500
Therefore, the cost allocated to the land is $32,500. This allocation is based on the relative appraised value of the land compared to the total appraised value of the real estate.
Learn more about multiply here:
https://brainly.com/question/23536361
#SPJ11
A population of insects consists of juveniles (1 year and under) and adults. Each year, 60% of juveniles reproduce and 80% of adults reproduce. 90% of juveniles survive to adulthood the next year and 0% of adults survive the year. The transition matrix for .6 .8 this population is then given by A = [.6 .8 ]
[.9 0 ]
(a) Find the eigenvalues of A. (b) Find an eigenvector corresponding to each of the eigenvalues. (c) Find the long term growth factor for the population and the long term population distribution.
Answers
(a) To find the eigenvalues of matrix A, we need to solve the characteristic equation det(A - λI) = 0, where λ is the eigenvalue and I is the identity matrix.
The matrix A is given as A = [0.6 0.8; 0.9 0]. Subtracting λI from A gives A - λI = [0.6 - λ 0.8; 0.9 0 - λ]. The determinant of A - λI is: det(A - λI) = (0.6 - λ)(-λ) - (0.8)(0.9) = -0.6λ + λ² - 0.72. Setting this determinant equal to zero and solving for λ gives the eigenvalues of A. (b) To find the eigenvectors corresponding to each eigenvalue, we need to solve the equation (A - λI)v = 0, where v is the eigenvector. (c) The long-term growth factor for the population is determined by the dominant eigenvalue of A. Since A is a 2x2 matrix, there will be one dominant eigenvalue and one eigenvalue that is less than 1 in magnitude. The dominant eigenvalue represents the long-term growth factor.
The long-term population distribution is given by the corresponding eigenvector to the dominant eigenvalue. The entries in the eigenvector represent the proportions of the population in each category (juveniles and adults) in the long term.
By calculating the eigenvalues and eigenvectors of matrix A, we can determine the long-term growth factor and population distribution for the given insect population.
To learn more about identity matrix click here:
brainly.com/question/2361951
#SPJ11
show that a countably infinite number of guests arriv- ing at hilbert’s fully occupied grand hotel can be given rooms without evicting any current guest.
Answers
The countably infinite number of guests can be accommodated by moving each current guest to the next room number (i.e., guest in room 1 moves to room 2, guest in room 2 moves to room 3, and so on) and then assigning the newly arrived guests to the vacated rooms (i.e., guest 1 goes to room 1, guest 2 goes to room 2, and so on).
This way, every guest still has a room and no one is evicted.
The solution to this problem relies on the fact that the set of natural numbers (which is countably infinite) can be put into one-to-one correspondence with the set of positive even numbers (also countably infinite).
This means that each current guest can be moved to the next room number without any gaps or overlaps, and the newly arrived guests can be assigned to the vacated rooms in the same manner.
The concept of one-to-one correspondence is fundamental to understanding countability and infinite sets, and it plays a key role in many mathematical proofs and arguments.
To know more about natural numbers click on below link:
https://brainly.com/question/17429689#
#SPJ11
Use front-end estimation to estimate the difference.
92.1 - 18.56
70
50
60
80
Answers
Answer:
70 is the answer.....Thank you ☺️
I NEED HELP ASAP A store sold a case of scented candles for $18.00 that had been marked up 20%. What was the original price?
Answers
Answer:15
Step-by-step explanation:
Omar grouped the terms and factored the GCF out of the groups of the polynomial 3x3 – 15x2 – 4x + 20. His work is shown.
Step 1: (3x3 – 15x2) + (–4x + 20)
Step 2: 3x2(x – 5) + 4(–x + 5)
Omar noticed that he does not have a common factor. Which accurately describes what Omar should do next?
Omar should realize that his work shows that the polynomial is prime.
Omar should go back and regroup the terms in Step 1 as (3x3 – 15x2) – (4x + 20).
In Step 2, Omar should factor only out of the first expression.
Omar should factor out a negative from one of the groups so the binomials will be the same.
Answers
Answer:
2nd option
Step-by-step explanation:
Given
3x³ - 15x² - 4x + 20
step 1 ( group the first/second and third/fourth terms )
(3x³ - 15x² ) + (- 4x + 20)
step 2 ( factor each group )
3x² (x - 5) - 4(x - 5) ← note factor of - 4 ( not + 4 )
step 3 ( factor out (x - 5) from each term )
(x - 5)(3x² - 4)
Answer:
ITS D !!!!
Step-by-step explanation:
got it right on test
Need help with my geometry homework pls
Answers
Answer:
what is the question at hand?
Step-by-step explanation:
I'll gladly solve if you can provide a question?
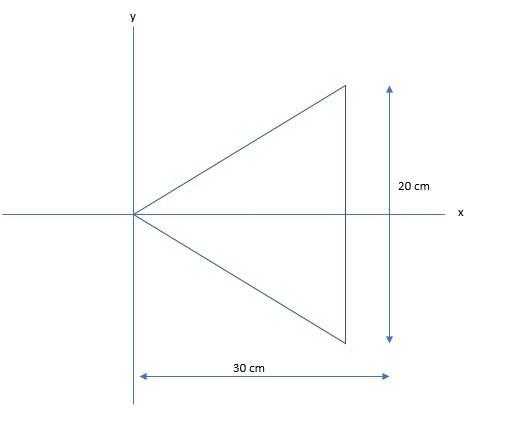
an 800 g steel plate has the shape of the isosceles triangle shown in the figure(figure 1).
Answers
The x- and y-coordinates of the center of mass are; (20, 0)
What is the center of mass of an object?The center of mass is the location where the sum of the relative position of the masses in a mass distribution is zero. It is the point where force can be applied on the distributed mass without causing a rotation of the system.
The mas of the steel plate = 800 g = 0.8 kg
The base length of the isosceles triangular plate = 20 cm = 0.2 m
The height of the isosceles triangular plate = 30 cm = 0.3 m
Considering a small strip of height, dx and width, I, we get
Area of small strip, dA = I·dx
Density of the plate for a unit thickness, ρ = M/A
Density of the small strip of mass dm = dm/dA
Considering the density of the plate as uniform, we get;
\(\displaystyle {\frac{dm}{dA} =\frac{M}{A}\)
Therefore;
\(\displaystyle {dm=\frac{M}{A}\times dA}\)
The area of the triangular plate, A = (1/2) × 0.2 m × 0.3 m = 0.03 m²
Mass of the plate, M = 0.8 kg
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx}\)
The width of the small strip, I, located at a distance x from the vertex of the triangular plate, using similar triangles, indicates;
\(\dfrac{I}{20} = \dfrac{x}{30}\)
\(I=20\times \dfrac{x}{30} = \dfrac{2}{3} \cdot x\)
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx} = \frac{0.8}{0.03}\times \dfrac{2}{3} \cdot x\cdot dx}\)
The center of mass, \(x_{cm}\), can be obtained with the formula; \(\displaystyle {x_{cm} = \dfrac{1}{M} \cdot \int\limits {x} \, dm }\)
Therefore; \(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx }\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx } = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0\)
\(\displaystyle {x_{cm} = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0=\frac{200}{9} \times \frac{0.027}{3} =0.2\)
The location of the x-coordinate center of mass, \(x_{cm}\) = 0.2 m = 20 cm from the vertex, which is the same location as the x-coordinate of the centroid of the plate of uniform density.
The plate is symmetrical about the x-axis, therefore, the y-coordinate of the center of mass is along the x-axis, which is \(y_{cm}\) = 0
The coordinate of the center of mass = (0.2, 0)
Part of the question requires the location of the coordinate of the center of mass of the triangular plate
Learn more about the center of mass of regular shapes here:
https://brainly.com/question/28021242
#SPJ1

plz help with these ill post more with more points


Answers
Answer:
I think it is D I'm not sure
Step-by-step explanation:
If two angle and one ️ are congruent to two angles of a second ️ and also if the included sides are congruent, then the ️ are congruent. If in ️ PRQ and TUV, angle P=angle T, angle R=angle and PR=TU, then triangles PRQ is congruent to triangle TUV
f(-4)= x^2 + 4
The value of f(-4)
Answers
(-4)^2 + 4 = 16 + 4
The solution: f(-4) = 20
Answer:
f
(
2
)
=
6
Explanation:
To evaluate f(2), substitute x = 2 into f(x).
Step-by-step explanation:
data from central hudson labs determined the mean number of insect fragments in 225-gram chocolate bars was 14.4, but three brands had insect contamination more than twice the average. assume the number of fragments (contaminants) follows a poisson distribution. (a) if you consume a 225-gram bar from a brand at the mean contamination level, what is the probability of no insect contaminants?
Answers
The probability of finding 0 contaminated pieces in 225 g of chocolate is 5.57 X 10⁻⁷.
Here the number of contaminated fragments follows a Poisson process. Hence, let the distribution for the same be X.
Hence we get X ~ Poi(λt)
where λ is the mean no. of contaminated pieces and t is the no. of bars consumed.
For P(X = x) we get [(λt)ˣ e^(-λt)]/x!
Here λ = 14.4 and t = 1 Hence we will get
P(X = x) = [(14.4)ˣ e⁻¹⁴°⁴]/x!
Here we need to find the probability of the no. of contaminated pieces = 0
Therefore
P(X = 0) = [(14.4)⁰ e⁻¹⁴°⁴]/0!
Hence the probability of finding 0 contaminated pieces in a bar of chocolate is
P(X = 0) = e⁻¹⁴°⁴
= 5.57 X 10⁻⁷
know more about probability click here;
https://brainly.com/question/30060906
#SPJ4
ASAP!!!!!!!!! PLEASE help me with this question! This is really urgent! No nonsense answers please.

Answers
Answer:
Because <CBD is an inscribed angle and <CAD is a central angle with the same intercepted arc, m<CBD = 55°, or half of the measure of <CAD.
Step-by-step explanation:
The Inscribed Angle Theorem proves that an inscribed angle is half the measure of a central angle, if both the inscribed angle and the central angle intercepts the same arc.
Also, according to the inscribed angle theorem, an inscribed angle is ½ of the measure of the arc it intercepts.
Therefore, m<CBD is half of m<CAD, or half of the measure of the arc CD that they both intercept together.
Thus, m<CBD = 55°, which is ½ of m<arc CD.
m<arc CD = 110° = m<CAD.
m<CBD = ½ of m<CAD = 55°.
The statement that best describes the relationship between <CBD and <CAD is "Because <CBD is an inscribed angle and <CAD is a central angle with the same intercepted arc, m<CBD = 55°, or half of the measure of <CAD."
Help pls 6th grade math i will give brainliest

Answers
Answer:
Step-by-step explanation:
d,i
i,d
The population of the United States in 2002 was about 260,255,000. In 2012 it was 291,049,000. Find the percent change to the nearest whole percent.
The change in population was a_% _ .
Answers
I'm been doing this question about an hour still can't solve so I really need your help! Really appreciate if u do :D

Answers
Explanation:
1 hat = 45 dollars
6 hats = 6*45 = 270 dollars
1 phone = 40 dollars
4 phones = 4*40 = 160 dollars
total = $270 + $160 = $430
Felicia spent a total of $430. Since this amount of money leaves her account, this means we write a negative sign out front to end up with the final answer of -430
In other words, her account balance went down by $430 which is why we use a negative. If someone gave her $430, then the answer would be positive.
i have no clue what this one is can someone help

Answers
Answer:
the answer is b
Step-by-step explanation:
radius is half the number of diameter
what is the mean absolute error?
Answers
Answer:
Step-by-step explanation: Mean Absolute Error is a model evaluation metric used with regression models. The mean absolute error of a model with respect to a test set is the mean of the absolute values of the individual prediction errors over all instances in the test set.

i really need help with this please!! i need it by 12:00 tonight

