Please help me with this. If a rock is thrown upward on an exoplanet of a nearby star with initial velocity of 20 m/s its height in meters t seconds later is given by y = 20t - 1.87t².

Answers
The averages velocities are:
i) 14.39m/s
ii) 16.073 m/s
iii) 16.24 m/s
iiii) 16.26 m/s
And the instanteneous velocity is:
b) 16.24 m/s
How to get the average velocity?We know that the vertical height is given by:
y(t) = 20t - 1.87t²
Then the velocity function will be:
v(t) = 20 - 2*1.87*t
v(t) = 20 - 3.74*t
To get the average velocity on an interval [a, b] we need to compute:
v' = (v(b) - v(a))/(b - a)
i) interval [1, 2]
v' = (y(2) - y(1))/(2 - 1)
v' = (20*2 - 1.87*2² - (20 - 1.87)//(2 - 1) = 14.39m/s
ii) interval [1, 1.1]
v' = (y(1.1) - y(1))/(1.1 - 1) = 1.6073/0.1 =16.073 m/s
iii) [1, 1.01]
v' = (y(1.01) - y(1))/(1.01 - 1) = 16.24 m/s
iiii) v' = (v(1.001) - v(1))/(1.001 - 1) = 16.26 m/s
b) to get the instantaneous velocity, just evaluate in t = 1.
v(1) = 20 - 3.74*1 = 16.26 m/s
Laern more about velocity at:
https://brainly.com/question/4931057
#SPJ1
Related Questions
Pineapple Street intersects Plum Street and Apple Street at their midpoints. Your home is at point P. You leave your home and jog down Plum Street to Kiwi Street, over Kiwi Street to Apple Street, up Apple Street to Pineapple Street, over Pineapple Street to Plum Street and then back home up Plum Street. How many miles did you jog?
Answers
Answer:
7.125 miles
Step-by-step explanation:
Using the triangle midsegment theorem:
Distance of pineapple street = 1/2(distance of kiwi street) = 0.5 * 1.4 = 0. 7 miles
Distance of plum Street = (2 * distance of P to Pineapple street) = 2 * 1.3 = 2.6 miles
Distance from Kiwi to pineapple = 1/2 * distance of apple Street = 0.5 * 2.25 = 1.125 miles
1.3 + 1.3 + 1.4 + 1.125 + 0.7 + 1.3

1. Find the m
2. Determine the length of side AB.
3. What are the sine and cosine ratios for angles A and B?
sin
cos
sin
cos
4. What do you notice about the sine of angle A and cosine angle B?
5. What do you notice about the cosine of angle A and the sine of angle B?
6. Add up angles A and B. What do they equal?
7. Given the information you obtained in numbers 1-5, determine the kissing angles in A-D below.
a. sin40 degrees=cos
b. cos27 degrees= sin
c. sin90 degrees = cos
d. cos65 degrees = sin

Answers
Step-by-step explanation:
remember, the sum of all angles in a triangle is always 180°.
1. you mean find the angle at A, yes ?
180 = angle A + angle B + angle C =
= angle A + 38 + 90
angle A = 180 - 38 - 90 = 90 - 38 = 52°
2. Pythagoras
AB² = 11² + 8.5² = 121 + 72.25 = 193.25
AB = 13.90143877... in
3. sine/cosine ratio is tangent.
sin(38) × AB = 8.5 in
cos(38) × AB = 11 in
sin(38)/cos(38) = tan(38) = 8.5/11 = 0.772727272...
sin(52) × AB = 11 in
cos(52) × AB = 8.5 in
sin(52)/cos(52) = tan(52) = 11/8.5 = 1.294117647...
4. they are equal. as sin(x) = cos(90-x).
5. they are equal. as cos(x) = sin(90-x).
6. 90°. again, the sum of all angles must be 180°. so, when one angle is all by itself already 90°, then there are only 90° left for the other 2 angles.
7. not sure what you mean by "kissing angles" but
a. sin(40°) = cos(90-40) = cos(50°) = 0.64278761...
b. cos(27°) = sin(90-27) = sin(63°) = 0.891006524...
c. sin(90°) = cos(90-90) = cos(0°) = 1
d. cos(65°) = sin(90 - 65) = sin(25°) = 0.422618262...
One jar of spaghetti sauce is made with ⅔ of a cup of tomatoes. How many jars of spaghetti sauce can be made with 3 cups of tomatoes?
Answers
Answer:
2
Step-by-step explanation:
Multiply 2/3 by 3 to get 2.
Write 3 1/2 cups as a multiplication expression using the unit, 1 cup, as a factor.
I ABSOLUTELY NEED HELP BY TOMORROW!!! I AM GIVING 100 POINTS

Answers
3 1/2 cups can be expressed as the multiplication expression: 3 + 1/2.
How to Write 3 1/2 cups as a multiplication expression using the unit, 1 cup, as a factor.To express 3 1/2 cups as a multiplication expression using the unit "1 cup" as a factor, you can write it as:
3 1/2 cups = (3 + 1/2) cups = 3 cups + 1/2 cup
Since there are 1 cup in each term, we can rewrite it as:
3 cups + (1/2) cup
Now, we can express each term as a multiplication expression:
3 cups = 3 * 1 cup = 3
(1/2) cup = (1/2) * 1 cup = 1/2
Putting it all together, the multiplication expression is:
3 * 1 cup + (1/2) * 1 cup = 3 + 1/2
Therefore, 3 1/2 cups can be expressed as the multiplication expression: 3 + 1/2.
Learn more about expression at https://brainly.com/question/1859113
#SPJ1
solve simultaneously 2x - y = - 10 and 3x + 2y = - 1
Answers
The solution to the system of equations is x = -3 and y = -4.
To solve the system of equations:
Equation 1: 2x - y = -10
Equation 2: 3x + 2y = -1
We can use the method of substitution or elimination to find the values of x and y.
Let's use the method of elimination:
Multiply Equation 1 by 2 to make the coefficients of y in both equations equal:
2(2x - y) = 2(-10)
4x - 2y = -20
Now, we can eliminate y by adding Equation 2 and the modified Equation 1:
(3x + 2y) + (4x - 2y) = -1 + (-20)
7x = -21
x = -3
Substitute the value of x into Equation 1 to solve for y:
2(-3) - y = -10
-6 - y = -10
y = -10 + 6
y = -4
Therefore, the solution to the system of equations is x = -3 and y = -4.
for such more question on equations
https://brainly.com/question/17482667
#SPJ8
can you put this in order 2, 10, 9, -10, -9, -8, -7, -6, -5 -4, 0,
Answers
ORDER FROM LEAST TO GREATEST:
-10, -9, -8, -7,-6, -5, -4, 0, 2, 9, 10.
Hey there!
When we have negative numbers, we might count like this: ....-5,-4,-3,-2,-1,0,1,2,3....
As you can see, the negative number is known as greater if it is closer to zero, so -1 is greater than -100.
With this information, let's order these numbers! :)
-10,-9,-8,-7,-6,-5,-4,0,2,9,10
I hope that this helps!
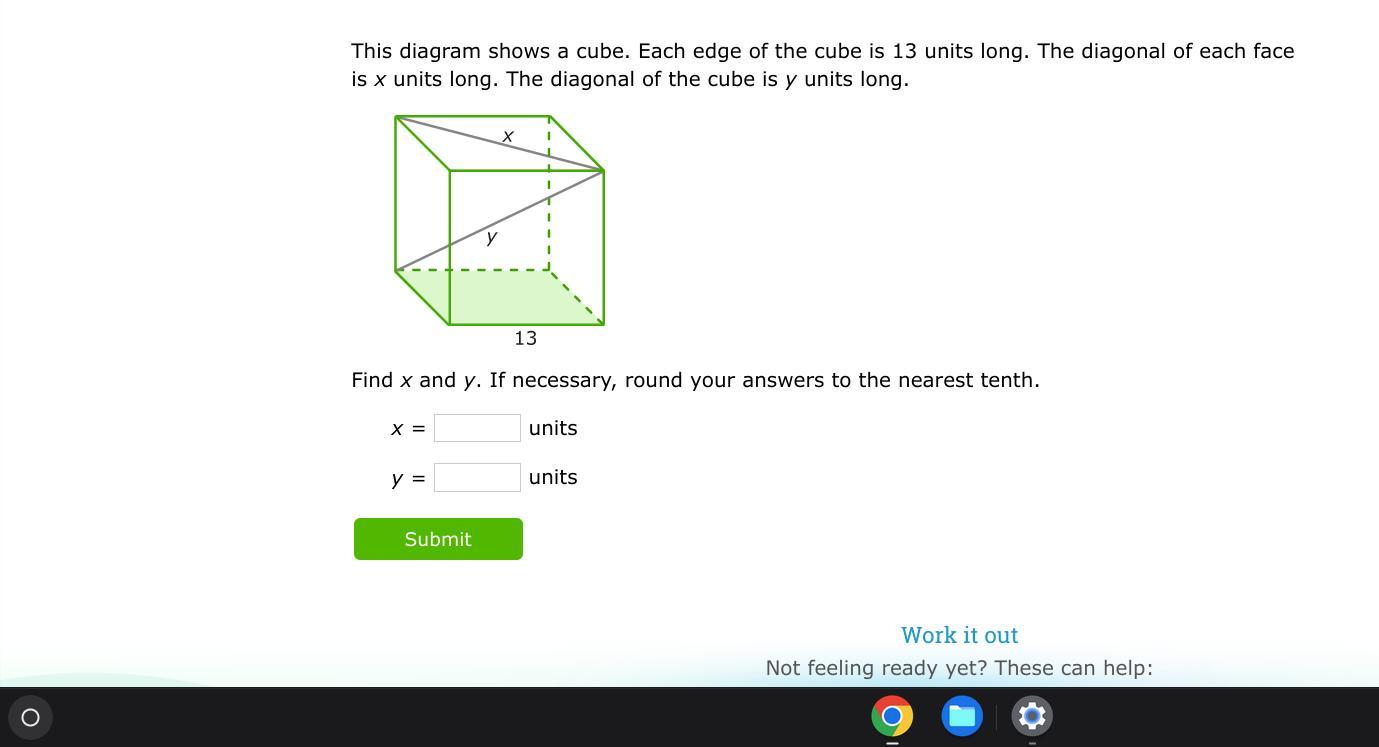
This diagram shows a cube. Each edge of the cube is 13 units long. The diagonal of each face is x units long. The diagonal of the cube is y units long.
Find x and y. If necessary, round your answers to the nearest tenth.
Answers
The value of x is 18.4 and the value of y is 22.5 in the cube
Finding the values of x and yFrom the question, we have the following parameters that can be used in our computation:
The diagram of a cube.
Each edge of the cube = 13 units.
The diagonal of each face is x units long
So, we have
x^2 = 13^2 + 13^2
Evaluate
x = 18.4
The diagonal of the cube is y units long.
So, we have
y^2 = 13^2 + 13^2 + 13^2
Evaluate
y = 22.5
Hence, the value of x is 18.4 and the value of y is 22.5
Read more about lengths at
https://brainly.com/question/24487155
#SPJ1
The seating capacity y for a banquet hall is represented by y = 8x + 56,
where x is the number of extra tables you need. How many extra tables
do you need to double the original seating capacity?
Answers
The number of extra tables that you need to double the original seating capacity will be 7.
What is the solution to the equation?The allocation of weights to the important variables that produce the calculation's optimum is referred to as a direct consequence.
The seating capacity y for a banquet hall is represented by y = 8x + 56, where x is the number of extra tables you need.
If the no extra table is there. Then the value of 'y' will be
y = 8 (0) + 56
y = 56
Then the number of extra tables do you need to double the original seating capacity will be
8x + 56 = 2 × 56
8x = 56
x = 7
Then the number of extra tables that you need to double the original seating capacity will be 7.
More about the solution of the equation link is given below.
https://brainly.com/question/545403
#SPJ1
What is the shape of the cross section of the figure that is perpendicular to the triangular bases and passes through a
vertex of the triangular bases?
A
a parallelogram that is not a rectangle
O a rectangle
O a triangle that must have the same dimensions as the bases
O a triangle that may not have the same dimensions as the bases
Answers
Answer:
a triangle that may not have the same dimensions as the bases
Step-by-step explanation:
The cross section of the figure that is perpendicular to the triangular bases and passes through a vertex of the triangular bases would be a triangle that may not have the same dimensions as the bases.
-10 -(-5) can someone answer dis for me please
.
Answers
Answer:
-5
Step-by-step explanation:
yw
Answer:
-5
Step-by-step explanation:
the two minus signs next to each other make it a plus sign so the equation would become
-10 + 5
which is -5
Please help with this, write an equation of the ellipse 18th a vertex at (-8,0) and a co-vertex at (0,4) and a center at (0, 0)
Answers
The equation of the ellipse that has the center at (0, 0) the vertex at (-8, 0), and the covertex at (0, 4) is; \(\frac{x^2}{64} + \frac{y^2}{16} = 1\)
What is the standard equation of an ellipse?The standard form of the equation of an ellipse is as follows;
\(\frac{x^2}{a^2} + \frac{y^2}{b^2}=1\)
Where;
a = The semi major axis
b = The semi minor axis
The semi major axis is the distance from the center of the ellipse to the vertex, and the semi minor axis is the distance from the center to the co-vertex.
The coordinate of the center of the ellipse = (0, 0)
The coordinates of the vertex = (-8, 0)
The coordinates of the co-vertex = (0, -4)
The ellipse has an horizontal major axis, therefore;
a = |0 - (-8)| = 8, and b = |0 - 4| = 4
The equation of the ellipse is therefore;
\(\frac{x^2}{8^2} + \frac{y^2}{4^2}=\frac{x^2}{64} + \frac{y^2}{16} = 1\)
\(\frac{x^2}{64} + \frac{y^2}{16} = 1\)
Learn more on the equation of an ellipse here: https://brainly.com/question/24545814
#SPJ1
6 to the power of 3 +7 times 4
Answers
Answer:
892
Step-by-step explanation:
Yolanda scored 10 points in a basketball game. She could have scored with one‐point free throws, two‐point field goals, or three‐point field goals. In how many different ways could she have scored her 10 points?
Answers
she could have scored the 10 points in 302400 ways.
The given parameters are
n= total points =10
r1 =one-point free throw = 1
r2 = two-point field goals = 2
r3 = three-point field goals = 3
The number of ways (k) she could have scored the points is:
k=(n!)/(r1!×r2!×r3!)
The factorial function is a mathematical formula represented by an exclamation mark "!".
k= 10!/(1!×2!×3!)
k= 3628800/(1×2×6)
k= 302400
so.. she could have scored the 10 points in 302400 ways.
To learn more about Combinations
visit : brainly.com/question/15301090
#SPJ9
which statement is true of the Y value of function I would ask equals -2 is greater than the Y value function be when I ask equals negative to the Y value function a 1X equals -2 is less than the Y value a function be one x was -2
Answers
The statement "the Y value of function I would ask equals -2 is greater than the Y value function be when I ask equals negative to the Y value function a 1X equals -2 is less than the Y value a function be one x was -2" is true.
Given, two functions y = -2f(x) = 1/x
To determine whether the statement "the Y value of function I would ask equals -2 is greater than the Y value function be when I ask equals negative to the Y value function a 1X equals -2 is less than the Y value a function be one x was -2" is true or false, we need to find the value of Y for both functions when x = -2.
Substituting x = -2 in the functions we get:I would ask y = -2(-2) = 4f(-2) = 1/(-2) = -1/2Therefore, the Y value of the function I would ask is greater than the Y value function be when I ask equals negative to the Y value function a 1X equals -2 is less than the Y value a function be one x was -2. Hence, the given statement is true.
Therefore, the statement "the Y value of function I would ask equals -2 is greater than the Y value function be when I ask equals negative to the Y value function a 1X equals -2 is less than the Y value a function be one x was -2" is true.
For more questions on value .
https://brainly.com/question/843074
#SPJ8
5(10-3)=8 pls answer
Answers
Answer:
5(10-3)=8 is False
Step-by-step explanation:
5(10-3)=35
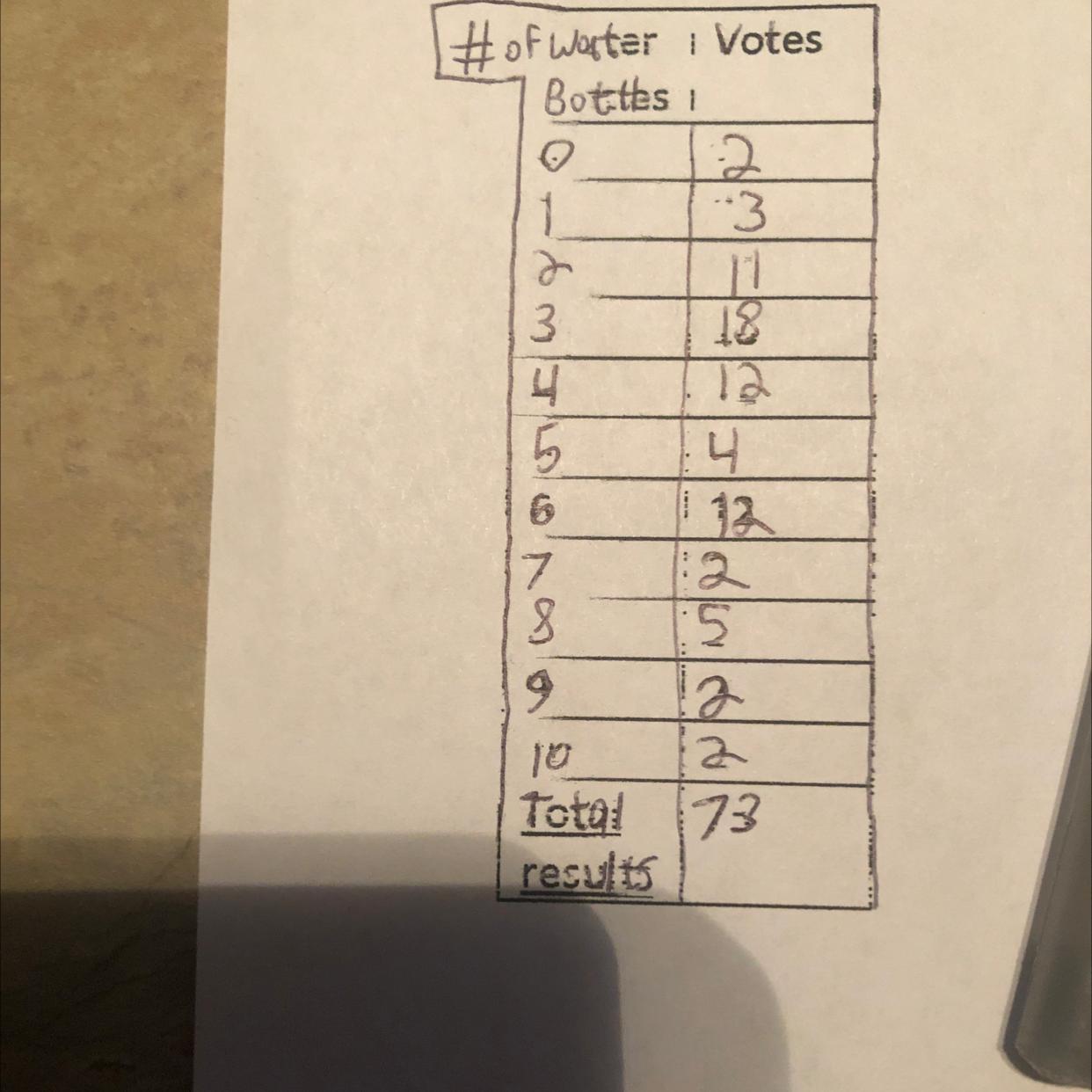
Can someone help create a frequency distribution with 5 classes using this data? Please I’d you can include the frequency
Answers
The required frequency distribution table is below in the solution part.
What is the relative frequency of the data?The relative frequency of the data is the ratio of the given frequency to the total frequency in the observation.
To create a frequency distribution with 5 classes, we first need to find the range of the data, which is the difference between the largest and smallest values:
Range = 10
Next, we divide the range by the number of classes we want (5) to get the class width:
Class width = Range / Number of classes
Class width = 10 / 5
Class width = 2
Now, we can create the frequency distribution table:
Class Frequency
0-1 5
2-3 29
4-5 16
6-7 14
8-9 2
10-11 2
___________________
Total 73
Learn more about the relative frequency here:
https://brainly.com/question/28354590
#SPJ1
A certain truck traveled 7,605 miles in 15 days. What is the average number of miles traveled per day?
Answers
If the certain truck traveled 7,605 miles in 15 days. The average number of miles traveled per day will be 507.
What is average?It is defined as the single number that represents the mean value for the given set of data or the closed value for each entry given in the set of data.
It is given that, a certain truck traveled 7,605 miles in 15 days.
The average number of miles traveled per day is obtained by dividing the total distance traveled by the total time taken as,
Suppose the average number of miles traveled per day is x,
x=76015 / 15
x=507 miles per day.
Thus, if the certain truck traveled 7,605 miles in 15 days. The average number of miles traveled per day will be 507.
Learn more about the average here:
brainly.com/question/24057012
#SPJ1
a rectangular with a perimeter of 32 cm has a base of x-3 cm and a height of 2x+7 cm what are the length in cm of the rectangle base an height
Answers
Answer:
Step-by-step explanation:
Perimeter = 32
length = x - 3
width = 2x + 7
Perimeter = 2* Length + 2* width
Perimeter = 2*(x-3) + 2(2x + 7) = 32 Remove the brackets.
2x - 6 + 4x + 14 = 32 Combine
6x + 8 = 32 Subtract 1 from both sides
6x = 32 - 8
6x = 24 Divide by 6
x = 24/6
x = 4
So the base = x - 3 = 4 - 3 = 1
The height = 2*4 + 7 = 8 + 7 = 15
5x-y=1/4 write in slope-intercept form
Answers
The slope intercept form of the given equation is,
y = 5x - 1/4
Given an equation of a line as,
5x - y = 1/4
We have to write the equation of the line in slope intercept form.
Equation of the line in slope intercept form is,
y = mx + c
Here m is the slope and c is the y intercept.
Rearranging the given equation,
5x = y + 1/4
5x - 1/4 = y
or,
y = 5x - 1/4
Hence the slope intercept form is y = 5x - 1/4.
Learn more about Slope intercept form here :
https://brainly.com/question/29146348
#SPJ1
I need some help with this

Answers
Answer:
(3) Median
Step-by-step explanation:
I would say median because it most likely wouldn't be any of the others. Mean would be thrown off with the outlier 0.80. Mode wouldn't really work for this. I don't think standard deviation would work because this isn't coninuous data.
Hope it helps and is correct!
If c(x) = 2x^2 - 4x + 3 and d(x) = -x^3 + x + 1 find c(3a)
Answers
Answer:
c(3a) = 2(3a)^2 - 4(3a) + 3 = 18a^2 - 12a + 3.
Step-by-step explanation:
c(3a) = 18a^2 - 12a + 3
Note: this is the simplified form of the expression.
Express the inverse of the following matrix (assuming it exists) as a matrix containing expressions in terms of k.
[-25 -25 -25]^-1 [0 0 0]
[ k 0 3] = [0 0 0]
[-5 -5 -3] [0 0 0]
Answers
Answer:
the Inverse of the matrix is; A⁻¹
\(= \left[\begin{array}{ccc}\frac{-3}{(2k)} &\frac{1}{k}&\frac{15}{(2k)}\\\frac{-3k+15}{(10k)}&\frac{-1}{k}&\frac{-75+13k}{(10k)}\\\frac{1}{2}&0&\frac{-5}{2}\end{array}\right]\)
Step-by-step explanation:
Given the data in the question;
Matrix A = \(\left[\begin{array}{ccc}-25&-25&-13\\k&0&3\\-5&-5&-3\end{array}\right]\)
To find the Inverse of matrix A
A⁻¹ = Adj.A / det.A
so
Determinant of the matrix A will be
|A| = -25( 0 + 15) + 25( -3K + 15 ) - 13( -15K + 0 )
= -375 - 75K + 375 + 65K
= -10K
Now, the adjoin of matrix A will be
Adj.A = \(\left[\begin{array}{ccc}15&-10&-75\\3k-15&10&75-13k\\-5k&0&25k\end{array}\right]\)
The Inverse of the matrix is;
A⁻¹ = Adj.A / det.A
\(= \frac{1}{-10k} \left[\begin{array}{ccc}15&-10&-75\\3k-15&10&75-13k\\-5k&0&25k\end{array}\right]\)
\(= \left[\begin{array}{ccc}\frac{15}{-10k} &\frac{-10}{-10k}&\frac{-75}{-10k}\\\frac{3k-15}{-10k}&\frac{10}{-10k}&\frac{75-13k}{-10k}\\\frac{-5k}{-10k}&\frac{0}{-10k}&\frac{25k}{-10k}\end{array}\right]\)
\(= \left[\begin{array}{ccc}\frac{-3}{2k} &\frac{1}{k}&\frac{15}{2k}\\\frac{-3k+15}{10k}&\frac{-1}{k}&\frac{-75+13k}{10k}\\\frac{1}{2}&0&\frac{-5}{2}\end{array}\right]\)
\(= \left[\begin{array}{ccc}\frac{-3}{(2k)} &\frac{1}{k}&\frac{15}{(2k)}\\\frac{-3k+15}{(10k)}&\frac{-1}{k}&\frac{-75+13k}{(10k)}\\\frac{1}{2}&0&\frac{-5}{2}\end{array}\right]\)
Therefore the Inverse of the matrix is; A⁻¹
\(= \left[\begin{array}{ccc}\frac{-3}{(2k)} &\frac{1}{k}&\frac{15}{(2k)}\\\frac{-3k+15}{(10k)}&\frac{-1}{k}&\frac{-75+13k}{(10k)}\\\frac{1}{2}&0&\frac{-5}{2}\end{array}\right]\)
A large diamond with a mass of 481.3 grams was recently discovered in a mine. If the density of the diamond is 3.51 grams over centimeters cubed, what is the volume? Round your answer to the nearest hundredth. 48.23 cm3 55.91 cm3 58.71 cm3 137.12 cm3
Answers
Since the mass of diamond is 481.3 g, the volume of diamond is 137.12 cm³
What is volume?Volume is the capacity of an object
Since large diamond with a mass of 481.3 grams was recently discovered in a mine. If the density of the diamond is 3.51 grams over centimeters cubed, to determine the volume of the diamond, we proceed as follow.
We know that density, ρ = m/v where
m = mass and v = volumeNow, since we desire the volume of the object, we make the volume subject of the formula, so, we have that
v = m/ρ
Given that
m = 481.3 g andρ = 3.51 g/cm³Substituting the values of the variables into the equation, we have that
v = m/ρ
= 481.3 g/3.51 g/cm³
= 137.123 cm³
≅ 137.12 cm³
So, the volume is 137.12 cm³
Learn more about volume of diamond here:
https://brainly.com/question/30394324
#SPJ1
Pls help I’ll mark u if ur right

Answers
Answer:
dividing by 1000
Step-by-step explanation:
in the context of dependent sample designs, all the extraneous variables should be included in the study as independent variables in order to determine their effects. (true or false)
Answers
False. No, extraneous variables should not be included as independent variables in the context of dependent sample designs.
In the context of dependent sample designs, extraneous variables should be controlled or accounted for in the study, but they should not be included as independent variables. This is because these extraneous variables are likely to be correlated with the dependent variable and including them would create an issue of multicollinearity that would affect the statistical analysis and interpretation of the results.
For example, when studying the effect of a new treatment on a group of patients, age, gender, and pre-existing health conditions may be considered as extraneous variables that should be controlled for, but not included as independent variables in the study. In this example, the formula for the regression analysis would be Y = β0 + β1X1 + β2X2 + e, where Y is the dependent variable, X1 and X2 are the independent variables, β0, β1, and β2 are coefficients, and e is the error term.
No, extraneous variables should not be included as independent variables in the context of dependent sample designs.
Learn more about independent variables here:
https://brainly.com/question/24127422
#SPJ4
Solve 4(5x+2)=14x+32
Answers
Answer:
x=4
Step-by-step explanation:
4(5x+2)=14x+32
20x+8 = 14x+32
20x-14x+8=14x-14x +32 (Both side +14x)
6x+8=32 (cancel 14x -14x)
6x+8-8=32 -8(both side -8)
6x=24 (both side divide 6)
6x/6=24/6
x=4
Answer:
34x+34
Step-by-step
20x+2=14x+32
20x+14x=2+32
34x+2+32
2+32=34
34x=34
Given f(x) = x - 1, g(x) = x2 - 1. Find
-
(fog)(x)
-
(gof)(x)
-
(fg)(x)
-
(gf)(x)
Answers
The solution for the following are as given below:(fog)(x) = x^2 - 2
(gof)(x) = x^2 - 2x
(fg)(x) = x^2 - 2
(gf)(x) = x^2 - 2x
How did we get the values?To compute the composition of two functions, we need to apply one function to the input, and then apply the second function to the output of the first function. For example, to compute (fog)(x), we first evaluate g(x), which gives us x^2 - 1, and then evaluate f(x^2 - 1), which gives us (x^2 - 1) - 1 = x^2 - 2. Similarly, we can compute (gof)(x) by evaluating f(x) = x - 1 first and then evaluating g(x - 1) = (x - 1)^2 - 1.
To compute the product of two functions, we simply multiply them together. For example, (fg)(x) = f(x) * g(x) = (x - 1) * (x^2 - 1) = x^3 - x^2 - x + 1. Similarly, we can compute (gf)(x) = g(x) * f(x) = (x^2 - 1) * (x - 1) = x^3 - 2x^2 + x + 1.
It's worth noting that the order of composition matters in general, which is why (fog)(x) and (gof)(x) give different results. However, in this particular case, since f and g are both quadratic polynomials, they happen to commute, meaning that (fog)(x) = (gof)(x) and (fg)(x) = (gf)(x).
We have:
(fog)(x) = f(g(x)) = f(x^2 - 1) = (x^2 - 1) - 1 = x^2 - 2
(gof)(x) = g(f(x)) = g(x - 1) = (x - 1)^2 - 1 = x^2 - 2x
(fg)(x) = f(g(x)) = f(x^2 - 1) = (x^2 - 1) - 1 = x^2 - 2
(gf)(x) = g(f(x)) = g(x - 1) = (x - 1)^2 - 1 = x^2 - 2x
Therefore:
(fog)(x) = x^2 - 2
(gof)(x) = x^2 - 2x
(fg)(x) = x^2 - 2
(gf)(x) = x^2 - 2x
learn more about function: https://brainly.com/question/10439235
#SPJ1
Find the sum of the following finite geometric series.

Answers
The sum of the geometric sequence in this problem is given as follows:
5.77.
What is a geometric sequence?A geometric sequence is a sequence of numbers where each term is obtained by multiplying the previous term by a fixed number, which is called the common ratio q.
The first term, the common ratio and the number of terms for this problem are given as follows:
\(a_1 = 10, q = -\frac{2}{3}, k = 8\)
The formula for the sum of the first n terms is given as follows:
\(S_n = a_1\frac{1 - r^n}{1 - r}\)
Hence the sum for this problem is given as follows:
\(S_8 = 10 \times \frac{1 - \left(-\frac{2}{3}\right)^8}{1 + \frac{2}{3}}\)
\(S_8 = 5.77\)
More can be learned about geometric sequences at brainly.com/question/24643676
#SPJ1
2
2780-4
Which is more, the average of the 4 even whole numbers from 8 to
15 or the average of the 4 odd whole numbers from 8 to 15?
Answers
After calculating the average of numbers here, the average of the four odd numbers from \(8 \ to \ 15\) is greater than the average of the four even numbers.
The step-by-step solution to this is given below:
To determine which average is greater, let's calculate the averages of the even and odd numbers separately.
The four even numbers from \(8 \ to \ 15 \ are \ 8, 10, 12, and \ 14\). To find their average, we sum them up and divide by \(4\):
\(\[\text{Average of even numbers} = \frac{8 + 10 + 12 + 14}{4} = \frac{44}{4} = 11\]\)
The four odd numbers from \(8 \ to \ 15 \ are \ 9, 11, 13, and \ 15.\) Similarly, we calculate their average:
\(\[\text{Average of odd numbers} = \frac{9 + 11 + 13 + 15}{4} = \frac{48}{4} = 12\]\)
Now, the next step will be comparing the two averages, we find that the average of the four odd numbers, \(12\), is greater than the average of the four even numbers, \(11\).
Therefore, the average of the four odd numbers from \(8 \ to \ 15\) is greater than the average of the four even numbers.
For more such questions on average on numbers: https://brainly.com/question/130657
#SPJ11
Solve the equation. X^5-5x^3+4x=0
Answers
Answer:
Wait
Step-by-step explanation:
Is a equation or polynomial
Answer:
0, +/- 1. +/- 2
Step-by-step explanation:
\(x^{5} -5x^{3} +4x=0\) Write the equation in the form of P(x) = 0.
\(x(x^{4} - 5x^{2} + 4) = 0\) Factor out the GCF, x.
\(x(x^{2})^{2} - 5x^{2} + 4 = 0\) Factor \((x^{2})^{2}- 5x^{2} + 4 = 0\).
\(x = 0,\) \((x^{2})^{2} - 5x^{2} + 4 = 0\) Let a = \(x^{2}\) and substitute.
\(a^{2} - 5a + 4 = 0\) Factor.
\((a - 4)(a - 1) = 0\) Replace a with \(x^{2}\).
\((x^{2} - 4)(x^{2} -1) = 0\) Factor \((x^{2} - 4)\) as a difference of squares.
\((x -2)(x+2)(x^{2} -1) = 0\) Use the Zero Product Property
\(x = 2, x = -2, x^{2} = -1\)
\(x = 0, 1, -1, 2, -2\)
