Peter picks one bill at a time from a bag and replaces it,
He repeats this process 100 times and records the results in
the table.
Peter's Experiment
Value Frequency
$1 28
14
$10 56
$20 2
Based on the table, which bill has an experimental
probability of 3 for being drawn from the bag next?
Answers
None of the bills have an experimental probability of 3, as all probabilities are between 0 and 1.
Based on the table, the experimental probability for each bill being drawn from the bag next can be calculated by dividing the frequency of each bill by the total number of draws (100). Using this formula, we can calculate the experimental probabilities for each bill:
1. For the $1 bill: Experimental probability = \(\frac{(Frequency of $1 bill)}{Total draws} = \frac{8}{100} = 0.28\)
2. For the $10 bill: Experimental probability =\(\frac{(Frequency of $10 bill)}{Total draws} = \frac{56}{100} = 0.56\)
3. For the $20 bill: Experimental probability =\(\frac{(Frequency of $20 bill)}{Total draws} = \frac{2}{100} = 0.02\)
None of the bills have an experimental probability of 3, as all probabilities are between 0 and 1.
To know more about "Probability" refer here:
https://brainly.com/question/30034780#
#SPJ11
Related Questions
determine if the taking the derivative of the function would be explicit or implicit. also if product, quotient, or chain rule would be needed.
Answers
To determine whether taking the derivative of a function would be explicit or implicit, as well as whether the product, quotient, or chain rule would be needed.
Taking the derivative of a function is explicit when the function is given explicitly in terms of the independent variable(s). In this case, we can easily differentiate the function by applying the standard differentiation rules without any additional steps.
On the other hand, taking the derivative of a function is implicit when the function is given implicitly, meaning it is defined implicitly in terms of the independent and dependent variables. The product rule is used when differentiating a product of two functions, the quotient rule is used when differentiating a quotient of two functions, and the chain rule is used when differentiating a composite function.
Learn more about composite function here:
https://brainly.com/question/30143914
#SPJ11
What is the slope of a line that is perpendicular to y=4/5x+15 and passes through point (-3,4)?
Answers
Answer:
Below
Step-by-step explanation:
The slope of the given line , m = 4/5
perpendicular slope is - 1/m = - 5/4
we can describe 15×-10 as an expression. we would describe 6×-2< 35 as an...
Answers
Answer: Inequality
Step-by-step explanation:
From the question, if we can describe 15×-10 as an expression, then we would describe 6×-2< 35 as an inequality. An
inequality is used to compare two values, and shows if one is less than, or greater than, or maybe not equal to the other value.
For example, a ≠ b means that a is not equal to b and a < b means a is less than b while a > b means a is greater than b. From the question, 6×-2< 35 means that 6x - 2 is less than 35.
A man places a 20 foot ladder against a 16 foot What is the measure of the angle formed by the ladder and the ground?
Answers
Answer:
is there any more context?
Step-by-step explanation:
Answer:
53.130°
Step-by-step explanation:
tan(x)=16/12
x is used in replacement of theta symbol
Look at the following graph and determine the slope of the line. AY 10 7 5 3 2 1 х 1 2 3 4 5 6 7 8 9 8 9 10
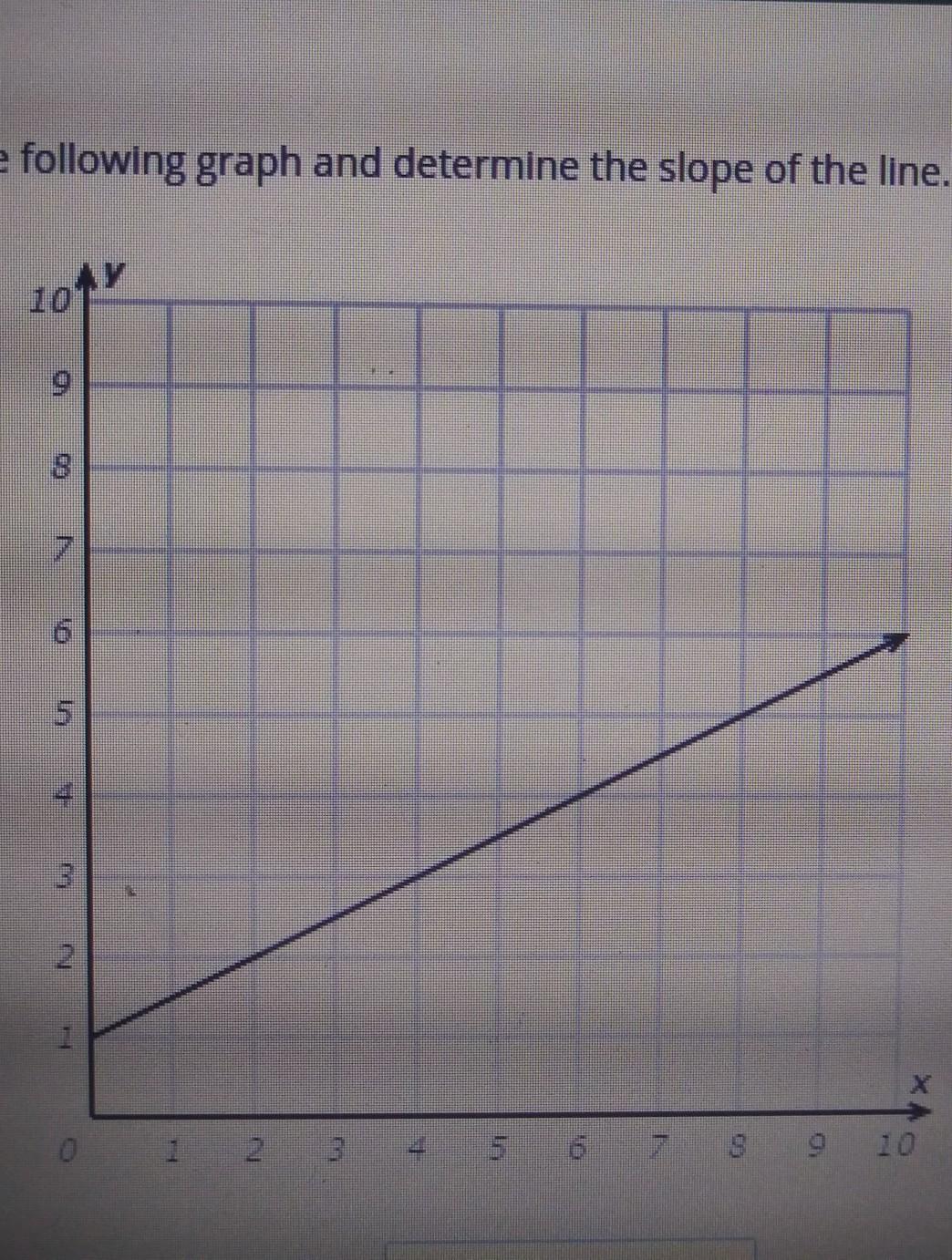
Answers
Answer:
I believe the slope is 2/3.
Compute the rate of return for an equipment that has an initial cost of 100,000 that would provide annual benefits of $22,500, annual maintenance cost of $4,500 with a salvage value of $18,700. Assume a useful life of 6 years.
Answers
The rate of return for the equipment is 12.03%.
How can the rate of return be calculated for an equipment ?The rate of return for the equipment can be calculated using the formula for the internal rate of return (IRR). The IRR is the discount rate that makes the net present value (NPV) of the cash flows equal to zero.
In this case, we have cash inflows of $22,500 per year, cash outflows of $4,500 per year for maintenance, and a salvage value of $18,700 at the end of the 6-year useful life. By applying the IRR formula, we find that the rate of return for the equipment is 12.03%.
Learn more about rate of return
brainly.com/question/17164328
#SPJ11
The rate of return for an equipment with an initial cost of $100,000, annual benefits of $22,500, annual maintenance cost of $4,500, and a salvage value of $18,700, over a useful life of 6 years, can be calculated using the internal rate of return (IRR) formula. The IRR is the discount rate that equates the present value of the cash inflows (benefits and salvage value) with the present value of the cash outflows (maintenance costs). By solving for the IRR, we find that the equipment's rate of return is 12.03%. This means that the equipment is expected to generate a 12.03% return on the initial investment over its useful life. The rate of return is a useful metric for evaluating the profitability and financial viability of investment projects. It helps decision-makers assess whether the project's returns exceed the required rate of return or cost of capital.
Learn more about calculating the rate of return and internal rate of return (IRR) for investment projects in finance and business decision-making.
#SPJ11
David invested $340 in an account paying an interest rate of 2\tfrac{1}{8}2 8 1 % compounded continuously. Natalie invested $340 in an account paying an interest rate of 2\tfrac{3}{4}2 4 3 % compounded quarterly. After 17 years, how much more money would Natalie have in her account than David, to the nearest dollar?
Answers
Answer:
$53.83
Step-by-step explanation:
For David
David invested $340 in an account paying an interest rate of 2\tfrac{1}{8}2 8 1 % compounded continuously.
r = 2 1/8% = 17/8% = 2.125% = 0.02125
t = 17 years
P = $340
For Compounded continuously, the formula =
A = Pe^rt
A = Amount Invested after time t
P = Principal
r = interest rate
t = time
A = $340 × e^0.02125 × 17
A = $ 487.94
For Natalie
Natalie invested $340 in an account paying an interest rate of 2\tfrac{3}{4}2 4 3 % compounded quarterly.
r = 2 3/4 % = 11/4% = 2.75% = 0.0275
t = 17 years
P = $340
n = compounded quarterly = 4 times
Hence,
Compound Interest formula =
A = P(1 + r/n)^nt
A = Amount Invested after time t
P = Principal
r = interest rate
n = compounding frequency
t = time
A = $340 (1 + 0.0275/4) ^17 × 4
A = $ 541.77
After 17 years, how much more money would Natalie have in her account than David, to the nearest dollar?
This is calculated as
$541.77 - $ 487.94
= $53.83
Hence, Natalie would have in her account, $53.83 than David
write the equation of the graphed in NO SPACES ALL LOWERCASE
Help !!

Answers
Answer:
The equation of the graphed line is:
y = 2Step-by-step explanation:
From the graph, it is clear that the line is a horizontal line at y = 2.
We know that a horizontal line has a slope of 0 because the value of y does not change no matter what the value of x we put in.
In other words, the equation of the horizontal line would always get the form:
y = k
where k is the y-intercept of the line.
Determining the y-intercept of the line:
We know that the value of the y-intercept can be determined by setting x = 0 and determining the corresponding value of y.
From the graph, it is clear
at x = 0, y = 2
Thus, the y-intercept k = 2
Thus, if we substitute the y-intercept k = 2 in the equation y = k, we get the equation
y = 2
Therefore, the equation of the graphed line is:
y = 2find the taylor polynomials p4 and p5 centered at a= π/6 for f(x)=5cos(x). p4 (x) = ____ . p5 (x) = ____
Answers
Both P₄(x) and P₅(x) are represented by the same expression.
\($P_5(x) = P_4(x) = \frac{2}{5} - \frac{2}{5}(x-6\pi) - \frac{4}{5}\left(\frac{1}{3}\right)(x-6\pi)^2 + \frac{8}{5}(x-6\pi)^3 + \frac{48}{5}\left(\frac{1}{3}\right)(x-6\pi)^4$\)
What is the polynomial equation?
A polynomial equation is an equation in which the variable is raised to a power, and the coefficients are constants. A polynomial equation can have one or more terms, and the degree of the polynomial is determined by the highest power of the variable in the equation.
To find the Taylor polynomials P₄ and P₅ centered at a = π/6 for f(x)= 5cos(x), we'll need to calculate the derivatives of f(x) and evaluate them at x= π/6.
We can then use these derivatives to construct the Taylor polynomials.
Let's start by finding the derivatives of f(x):
\(f(x) = 5\cos(x)$\\\\f'(x) = -5\sin(x)$\\$\\f''(x) = -5\cos(x)$\\\\$f'''(x) = 5\sin(x)$\\$\\f''''(x) = 5\cos(x)$\)
Now, let's evaluate these derivatives at x= π/6:
\(f\left(\pi/6\right) = 5\cos\left(\pi/6\right) = \frac{2}{5}$\\\\$f'\left(\pi/6\right) = -5\sin\left(\pi/6\right) = -\frac{2}{5}$\\\\$f''\left(\pi/6\right) = -5\cos\left(\pi/6\right) = -\frac{5}{3}$\\\\$f'''\left(\pi/6\right) = 5\sin\left(\pi/6\right) = \frac{2}{5}\\$\\$f''''\left(\pi/6\right) = 5\cos\left(\pi/6\right) = \frac{5}{3}$\)
Now, we can construct the Taylor polynomials:
The fourth degree Taylor polynomial P₄(x) centered at a = π/6 is given by:
\($P_4(x) = f\left(6\pi\right) + f'\left(6\pi\right)(x-6\pi) + \frac{2!}{2}f''\left(6\pi\right)(x-6\pi)^2 + \frac{3!}{3}f'''\left(6\pi\right)(x-6\pi)^3 + \frac{4!}{4}f''''\left(6\pi\right)(x-6\pi)^4$\)
Substituting the evaluated derivatives, we have:
Simplifying this expression will give you the specific form of P₄(x).
The fifth-degree Taylor polynomial P₅(x) centered at a = π/6 can be obtained by including one more term with the fifth derivative:
\($P_4(x) = \frac{2}{5} - \frac{2}{5}(x-6\pi) - \frac{4}{5}\left(\frac{1}{3}\right)(x-6\pi)^2 + \frac{8}{5}(x-6\pi)^3 + \frac{48}{5}\left(\frac{1}{3}\right)(x-6\pi)^4$\)
\($P_5(x) = P_4(x) = \frac{2}{5} - \frac{2}{5}(x-6\pi) - \frac{4}{5}\left(\frac{1}{3}\right)(x-6\pi)^2 + \frac{8}{5}(x-6\pi)^3 + \frac{48}{5}\left(\frac{1}{3}\right)(x-6\pi)^4$\)
Let's calculate the fifth derivative and complete the expression for P₅(x):
(since the derivative of sin(x) evaluated at π/6 is 0)
Hence, both P₄(x) and P₅(x) are represented by the same expression.
\($P_5(x) = P_4(x) = \frac{2}{5} - \frac{2}{5}(x-6\pi) - \frac{4}{5}\left(\frac{1}{3}\right)(x-6\pi)^2 + \frac{8}{5}(x-6\pi)^3 + \frac{48}{5}\left(\frac{1}{3}\right)(x-6\pi)^4$\)
To learn more about the polynomial equation visit:
brainly.com/question/1496352
#SPJ4
By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box may be made. If the cardboard is 16 in. long and 6 in. wide, find the dimensions (in inches) of the box that will yield the maximum volume. (Round your answers to two decimal places if necessary.)
Answers
Answer:
x=3.00 or x= 8.00
Explanation:
Let us denote side of the cut-out square as x inches
Then base of box = 16-2x by 6-2x
The volume = V = (16-2x)(6-2x)
= 96-3x-12x+4x
dV/dx = 96-44x+4x^2
= 0 for a max V
divide by 4
X^2 -11x +24=0
Using quadratic formula to solve the equation
X= (11± √11^2-(4×1×24)/2
(11± √25)/2
x= 3 or 8inches
From the equation of volume = V = x(16-2x)(6-2x)
Substitute
let x = 3 , V = 3(16-6)(6-6) = 0
let x = 8 , V = 8(16-16)(6-16) = 0
Therefore, the maximum volume exist at both point x=3 or x= 8
Ken is working this summer as part of a crew on a farm. He earned 8$ per hour for the first 10 hours for the rest of the week. Ken saves 90% of his earnings from each week. What is the least number of hours he must work the rest of the week to save at least 270$ for the week
Answers
He must work the rest of the 7 weeks to earn at least $270 for the week. 8
So we know that he's already earned $80 because he earned $8 per hour 9 for the first 10 hours.
So eight times 10 is 80.
Saving money helps you overcome difficult situations, meet your financial obligations, and build wealth. Saving money is essential. Provides financial security and freedom and covers financial emergencies. Saving money helps you avoid debt and reduces stress.
Saving is important because it helps cushion financial emergencies and unexpected expenses. In addition, savings can help you pay for big purchases, avoid debt, reduce financial stress, and increase your sense of financial freedom.
Learn more about saving money importance here: https://brainly.com/question/341992
#SPJ4
1 1/2 from -4 3/5
substract
Answers
Answer:
exact form: -101/10
decimal form: -10.1
mixed number: -10 1/10
(I couldn't tell if the four was seperated from the 3 so I tried my best to tell)
What is a double fact in 1st grade math?
Answers
Expression that has the same addend twice, such as 3 + 3 = 6 or 8 + 8 = 16
What do you mean by One-to-One Correspondence?
the capability of relating one object to another. For each number spoken aloud, the learner should be able to count or move one object while saying "1,2,3,4". She has not learned one-to-one correspondence if she accidentally counts an object twice or skips one of the things while counting. Before starting Giggle Facts, students must be able to match one object to each number counted.
Remind your kids that a double fact is a mathematical expression that has the same addend twice, such as 3 + 3 = 6 or 8 + 8 = 16. Give children the chance to practise combining groups of the same number using manipulatives or other classroom supplies.
Learn more about one-to-one correspondence link below
https://brainly.com/question/24138383
#SPJ4
Answer:
A double expression
Step-by-step explanation:
What is the equation that represents the line that passes through the points (9, -2) and (12, -5)?
Answers
Hi there!
\(\large\boxed{y = -x + 7}\)
To begin, we must use the slope formula to calculate the slope of the line:
\(m = \frac{y_2-y_1}{x_2-x_1}\)
Plug in the coordinates:
\(m = \frac{-5-(-2)}{12-9}\)
Simplify:
\(m = \frac{-3}{3} =-1\)
Recall that the equation for a line in point-slope form is:
y - y1 = m(x - x1)
Plug in coordinates into the equation along with the slope:
y - (-2) = -1(x - 9)
Simplify:
y + 2 = -x + 9
y = -x + 7
I NEED HELP AGAINNNNN
1) Are the triangles ABC and PQR in the diagram congruent? GIVE REASONS for your answer.
2) In a piggy bank, there are x numbers of one dollar bills and 2x number of 50 dollar bills. Find the total amount of money in the piggy bank, in terms of x.

Answers
Answer:
no they are not equal just look at the picture carefully and you will realise it's not equal
Vilma wants to have P350,000 at the end of 5 years by making a regular deposit at the end of each quarter in an account th pays 9.6% interest, compounded every 3 months. a. Find the amount of quarterly deposit. P b. Find the accumulated amount in the account after the 15 th deposit. rho
Answers
a. The amount of the quarterly deposit is approximately $5,573.39.
b. The accumulated amount in the account after the 15th deposit is approximately $128,523.79.
a. To find the amount of the quarterly deposit, we can use the formula for the future value of an ordinary annuity. The formula is:
A = P * ((1 + r)^n - 1) / r
Where:
A = Accumulated amount
P = Quarterly deposit
r = Interest rate per compounding period
n = Number of compounding periods
In this case, the interest is compounded every 3 months, so the interest rate per compounding period is 9.6% / 4 = 2.4%.
a. To find the quarterly deposit, we need to solve the formula for P. Rearranging the formula, we have:
P = A * r / ((1 + r)^n - 1)
Substituting the given values:
A = $350,000 (the desired accumulated amount)
r = 2.4% (0.024 as a decimal)
n = 5 years * 4 quarters per year = 20 quarters
P = $350,000 * 0.024 / ((1 + 0.024)^20 - 1)
P ≈ $5,573.39
Therefore, the amount of the quarterly deposit is approximately $5,573.39.
b. To find the accumulated amount after the 15th deposit, we can use the future value of an ordinary annuity formula but with a different value for n. Since the interest is compounded every 3 months, the number of compounding periods is 15 quarters.
A = P * ((1 + r)^n - 1) / r
Substituting the given values:
P = $5,573.39 (the calculated quarterly deposit)
r = 2.4% (0.024 as a decimal)
n = 15 quarters
A = $5,573.39 * ((1 + 0.024)^15 - 1) / 0.024
A ≈ $128,523.79
Therefore, the accumulated amount in the account after the 15th deposit is approximately $128,523.79.
Learn more about 'future value of an ordinary annuity':
https://brainly.com/question/25792915
#SPJ11
What is the area of the trapezoid shown?

Answers
Step-by-step explanation:
77 ft
Answer:
101.5 ft^2
Step-by-step explanation:
The area of a trapezoid is given by
A = 1/2 (b1+b2) h where b1 and b2 are the lengths of the bases and h is the height
A = 1/2 ( 11+18) * 7
= 1/2 (29) *7
101.5 ft^2
Find the slope of the table.

Answers
Answer:
Slope= -4
Step-by-step explanation:
Slope is rise over run (y over x)
So, looking at the table, you can see that every time the y values went down by 8, the x values went up by 2.
So, the slope can be written as:
-8/2
Simplified to -4/1 or just -4
Find the volume of the sphere:
A. 452.4 cubic meters
B. 904.8 cubic meters
C. 150.8 cubic meters
D. 36 cubic meters

Answers
Work Shown:
r = 6 = radius
V = volume of a sphere of radius r
V = (4/3)*pi*r^3
V = (4/3)*pi*6^3
V = 904.77868423386
V = 904.8
I used my calculator's stored version of pi (instead of something like pi = 3.14)
The units "cubic meters" can be abbreviated to m^3 or \(m^3\)
The volume of the given sphere is 904.8 cubic meters. Thus, option B is the answer.
The volume of a sphere can be calculated using the formula:
V = \(4/3 * \pi * r^3\),
Where V is the volume and r is the radius of the sphere.
\(\pi\) = 3.14
The radius of the sphere (r) = 6m
Plugging in the given radius of 6m into the formula, we get:
V = (4/3) * \(\pi\) * (6^3)
V = 1.333 * \(\pi\) * 216
V = 1.333 * 3.14 * 216
V = 4.1866 * 216
V = 904.8 cubic meters
Therefore, when the radius of the sphere is 6m, the volume of the sphere is 904.8 cubic meters.
To practice more problems based on the sphere:
https://brainly.com/question/28228180
Given the data below, test the hypothesis that job satisfaction (0 to 100 scale) is the same at Baruch
College and Brooklyn College. Test at the .05 level of significance.
Baruch College: mean job satisfaction score = 83.0; standard deviation = 15; n = 150.
Brooklyn College: mean job satisfaction score = 73.0; standard deviation = 12; n = 100.
The calculated value of the test statistic is:
Answers
The calculated value of the test statistic is approximately 6.40.
To test the hypothesis that job satisfaction is the same at Baruch College and Brooklyn College, we can use a two-sample t-test.
The null hypothesis (H0) assumes that the means of the two populations are equal, while the alternative hypothesis (Ha) assumes that the means are not equal.
H0: μ1 = μ2 (Mean job satisfaction at Baruch College is equal to mean job satisfaction at Brooklyn College)
Ha: μ1 ≠ μ2 (Mean job satisfaction at Baruch College is not equal to mean job satisfaction at Brooklyn College)
We can calculate the test statistic using the formula:
t = (x1 - x2) / sqrt((s1^2 / n1) + (s2^2 / n2))
where x1 and x2 are the sample means, s1 and s2 are the sample standard deviations, n1 and n2 are the sample sizes.
Given the data:
Baruch College: mean job satisfaction score (x1) = 83.0, standard deviation (s1) = 15, sample size (n1) = 150.
Brooklyn College: mean job satisfaction score (x2) = 73.0, standard deviation (s2) = 12, sample size (n2) = 100.
Calculating the test statistic:
t = (83.0 - 73.0) / sqrt((15^2 / 150) + (12^2 / 100))
t = 10 / sqrt(1 + 1.44)
t ≈ 10 / sqrt(2.44)
t ≈ 10 / 1.561
t ≈ 6.40
To learn more about statistic visit:
brainly.com/question/32201536
#SPJ11
If z is directly proportional to the product of x and y and if z is 10 when x is 4 and y is 5, then x, y, and z are related by the equation
Answers
The equation relating x, y, and z is:
z = 0.5 * x * y.
In the given problem, the relationship between x, y, and z can be expressed by the equation z = k * x * y, where k represents the constant of proportionality. By substituting the values of x = 4 and y = 5, when z is equal to 10, we can determine the value of the constant of proportionality, k, and further define the relationship between the variables.
To find the constant of proportionality, we substitute the known values of x = 4, y = 5, and z = 10 into the equation z = k * x * y. This gives us the equation 10 = k * 4 * 5. By simplifying the equation, we have 10 = 20k. To isolate k, we divide both sides of the equation by 20, resulting in k = 0.5. Therefore, the equation relating x, y, and z is z = 0.5 * x * y, meaning that z is directly proportional to the product of x and y with a constant of proportionality equal to 0.5.
To learn more about proportionality, click here: brainly.com/question/28194586
#SPJ11
Evaluate the expression
z + 3x4
A. 27
B. 32
C. 56
D. 1,304
Answers
The value of the expression z + 3x4 using arithmetic operation where z = 15, is 27. The answer is A) 27.
The given expression is z + 3x4, where z = 15. To evaluate this expression, we substitute 15 for z and perform the multiplication. First, we multiply 3 and 4, which gives us 12. Then, we add 15 and 12 to get the final result of 27.
z + 3x4 = 15 + 3x4
= 15 + 12
= 27
Therefore, the value of the expression when z = 15, is 27. In other words, using arithmetic operation of multiplication and addition, which gives us the final answer of 27. So, the correct answer is option A).
To know more about evaluating the expression:
https://brainly.com/question/2889219
#SPJ4
____The given question is incomplete , the complete question is given below:
Evaluate the expression, where z = 15
z + 3x4
A. 27
B. 32
C. 56
D. 1,304
What is the value of the expression 25 ÷ 5 + (6 x 2) − 4?
Question 1 options:
7
9
12
13
Answers
Answer:
13
Step-by-step explanation:
25 / 5 + 12 - 4 = 5 + 12 - 4 = 17 - 4 = 13
a cylindrical tank has a diameter of 24 dm And a height of 30, dm.how many litters of a water can it hold when full (1 dm³ = 1 L)
Answers
R = 12
To find the area of a circle you must do (R)^2 x Pi (3.14)
Meaning you must do:
12 x 12 = 144 = (R)^2
144 x (3.14) Pi = 452.16
Next we need to find the volume of the tank, by using the area of the circle we can now use the formula Area ((R)^2 xPi (3.14)) x height
We know the height equals 30dm so:
452.16 x 30 = 13,564.8
As it is 1dm^3 to 1L we don’t need to divide anything to equal them as they are the same meaning the answer is
13,564.8 Litres
Solve the linear equation
3.4 + 2(9.7 – 4.8x) = 61.2
Answers
55% of what number is 77?
Answers
Answer:
42.35
Step-by-step explanation:
hope it helps po.
Answer:
The number is 140
Step-by-step explanation:
Let n be the unknown number
of means multiply, is means equals
55% * n = 77
Change to decimal form
.55n = 77
Divide by .55
.55n/.55 = 77/.55
n =140
The number is 140
Write an equation in slope intercept form to represent luis's ride from his house to the beach. If Raul lives 5 miles closer to the beach than luis, at what speed must Raul ride for the plan to work?
Answers
Slope-intercept form
I'm confused need help :/

Answers
3x-2y=7
3x=7+2y we add 2y to move it to the other side
3x-7=2y We subtract seven to have 1y by itself and then divide by two to get it into simplified slope intercept form
Answers=
3/2x-3.5=y or written as=
y=3/2x-3.5
Answer:
y = 3/2x -7/2
Step-by-step explanation:
Solve for y.
\(3x -2y=7\qquad\text{given}\\\\3x=2y+7\qquad\text{add $2y$ to both sides}\\\\3x-7=2y\qquad\text{subtract 7}\\\\\dfrac{3}{2}x-\dfrac{7}{2}=y\qquad\text{divide by 2}\\\\\boxed{y=\dfrac{3x}{2}-\dfrac{7}{2}}\)
_____
Additional comment
Whatever operation is performed on the equation must be performed on both sides of the equation in order for the equal sign to remain valid. For example, when we say "subtract 7", you should understand that to mean "subtract 7 from both sides of the equation."
What is the range of the function?

Answers
***HOPE This Help You***
Jaylin has a scale model of a train to some centimeters in the model represents 3 feet in a real train on the scale model the two wheels of Jaylin true or 3.5 cm apart there are some old railroad tracks in the Wyoming that are 4.5 feet apart would the real train be able travel on those tracks?
Answers
5.25 or 5 1/4
I worked it out I hope this helps :)