☆*: .。. o(≧▽≦)o .。.:*☆ wasting my points
Answers
Answer:
Step-by-step explanation:
Totally rad!
Related Questions
sovle bpleaseeeeeeeeeedeeeeeeeeeeeeeeeeeeeeeeeeeese

Answers
Answer:
24 divided by 6 equals 4
Step-by-step explanation:
Answer: I think is 4
Step-by-step explanation:
HBI inc. seeks to schedule manual labor for 18 new homes being constructed. Historical data leads HBI to apply a 92 % learning curve rate to the manual labor portions of the project. If the first home requires 3,500 manual labor hours to build, estimate the time required to build:
a. the 5th house
b. the 10th house
c. all 18 houses
d. What would the manual labor estimate be for all 18 of the HBI houses in the problem above if the learning curve rate is 1) 70% 2) 75% 3) 80%
Please use a excel spreadsheet and explain how you got your answers in the excel spreadsheet with what to do and how to do it.
Answers
Using a 92% learning curve rate, the estimated manual labor hours required to build the 5th house would be 1,034 hours, the 10th house would be 692 hours, and all 18 houses combined would require 3,046 hours. Additionally, if the learning curve rates are 70%, 75%, and 80%, the estimated manual labor hours for all 18 houses would be 5,177, 4,308, and 3,636 hours, respectively.
The learning curve formula is given by \(Y = a * X^b\), where Y represents the cumulative average time per unit, X represents the cumulative number of units produced, a is the time required to produce the first unit, and b is the learning curve exponent.
In this case, the learning curve rate is 92%, which means the learning curve exponent (b) is calculated as log(0.92) / log(2) ≈ -0.0833.
a. To estimate the time required to build the 5th house, we can use the learning curve formula:
\(Y = a * X^b\)
\(Y(5) = 3500 * 5 ^ (-0.0833)\)
Y(5) ≈ 1034 hours
b. Similarly, the time required to build the 10th house can be estimated:
\(Y(10) = 3500 * 10^(-0.0833)\)
Y(10) ≈ 692 hours
c. The cumulative time required to build all 18 houses can be estimated by summing the individual estimates for each house:
\(Y(18) = 3500 * 18^(-0.0833)\)
Y(18) ≈ 3046 hours
d. To calculate the manual labor estimates for all 18 houses using different learning curve rates, we can apply the respective learning curve exponents to the formula. The results are as follows:
- For a 70% learning curve rate: Y(18) ≈ 5177 hours
- For a 75% learning curve rate: Y(18) ≈ 4308 hours
- For an 80% learning curve rate: Y(18) ≈ 3636 hours
In conclusion, using the given learning curve rate of 92%, the estimated time required to build the 5th house is 1034 hours, the 10th house is 692 hours, and all 18 houses combined would require 3046 hours. Additionally, different learning curve rates yield different manual labor estimates for all 18 houses.
Learn more about learning curve here:
https://brainly.com/question/5520587
#SPJ11
The pressure of a certain gas in atmospheres, p, and its corresponding volume in liters, v, are shown in the table. A two column table with 6 rows. The first row, v, has the entries, 1, 2, 3, 4, 5. The second column, p, has the entries, 3.00, 1.50, 1.00, 0.75, 0.60. For the points in the table, does pressure vary directly with volume? If so, identify k and write an equation. No, this is not a direct variation. Yes, this is a direct variation with k = . Yes, this is a direct variation with k = 1. Yes, this is a direct variation with k = 3.
Answers
Answer: No, this is not a direct variation.
Step-by-step explanation: Pressure (p) does not directly vary with volume (v).
Hope this helps! :)
Answer:
The answer is the first one
No, this is not a direct variation.
Step-by-step explanation:
Edge2020
Create the B-Tree Index (m=4) after insert the following input index: (7 pts.) 12,13,10,5,6,1,2,3,7,8,9,11,4,15,19,16,14,17
Answers
The B-Tree index (m = 4) after inserting the given input index
[10, 13]
/ \
[1, 2, 3, 4, 5, 6, 7, 8, 9] [11, 12] [14, 15, 16, 17, 19]
To create a B-Tree index with m = 4 after inserting the given input index, we'll follow the steps of inserting each value into the B-Tree and perform any necessary splits or reorganizations.
Here's the step-by-step process:
1. Start with an empty B-Tree index.
2. Insert the values in the given order: 12, 13, 10, 5, 6, 1, 2, 3, 7, 8, 9, 11, 4, 15, 19, 16, 14, 17.
3. Insert 12:
- As the first value, it becomes the root node.
4. Insert 13:
- Add 13 as a child to the root node.
5. Insert 10:
- Add 10 as a child to the root node.
6. Insert 5:
- Add 5 as a child to the node containing 10.
7. Insert 6:
- Add 6 as a child to the node containing 5.
8. Insert 1:
- Add 1 as a child to the node containing 5.
9. Insert 2:
- Add 2 as a child to the node containing 1.
10. Insert 3:
- Add 3 as a child to the node containing 2.
11. Insert 7:
- Add 7 as a child to the node containing 6.
12. Insert 8:
- Add 8 as a child to the node containing 7.
13. Insert 9:
- Add 9 as a child to the node containing 8.
14. Insert 11:
- Add 11 as a child to the node containing 10.
15. Insert 4:
- Add 4 as a child to the node containing 3.
16. Insert 15:
- Add 15 as a child to the node containing 13.
17. Insert 19:
- Add 19 as a child to the node containing 15.
18. Insert 16:
- Add 16 as a child to the node containing 15.
19. Insert 14:
- Add 14 as a child to the node containing 13.
20. Insert 17:
- Add 17 as a child to the node containing 15.
The resulting B-Tree index (m = 4) after inserting the given input index will look like this:
```
[10, 13]
/ \
[1, 2, 3, 4, 5, 6, 7, 8, 9] [11, 12] [14, 15, 16, 17, 19]
```
Each node in the B-Tree is represented by its values enclosed in brackets. The children of each node are shown below it. The index values are arranged in ascending order within each node.
Please note that the B-Tree index may have different representations or organization depending on the specific rules and algorithms applied during the insertion process. The provided representation above is one possible arrangement based on the given input.
To know more about B-Tree index, visit:
https://brainly.com/question/33169926#
#SPJ11
What is the equation of the line? YA -1 1 X y=2x-4 y=2x- 1 1 ==x+2 2 y = y = 2x + 2

Answers
Answer: \(y=\frac{1}{2}x+2\)
Step-by-step explanation:
Using the points \((0, 2)\) and \((2, 3)\), the slope of the line is \(\frac{3-2}{2-0}=\frac{1}{2}\).
Since the y-intercept is 2, the equation is \(y=\frac{1}{2}x+2\).
help pls i’m just guessing i don’t understand

Answers
Answer:
70
Step-by-step explanation:
Since the angle 2 is alternate angle to angle 6,they are both equal. So, the angle 6 is 70.
find the indicated length
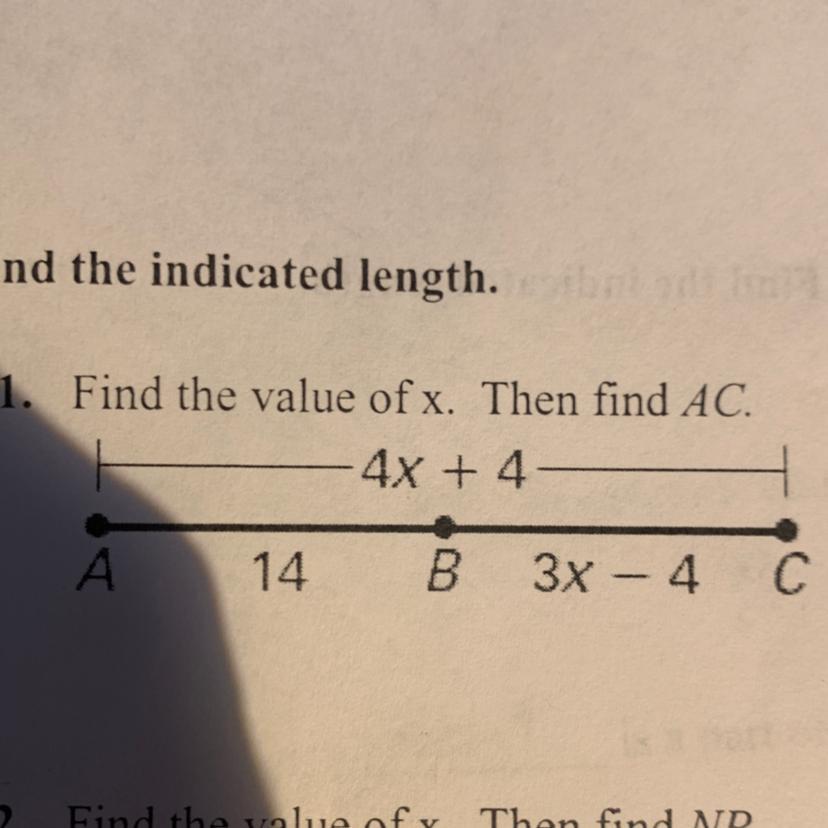
Answers
Answer:
x=6
AC = 28
Step-by-step explanation:
4x+4= AC
4x +4 = 14 + 3x -4
4x-3x= 14-4-4
x = 6
AC = 4(6) +4 = 24+4 = 28
the number of categorical outcomes per trial for a multinomial probability distribution is
Answers
The number of categorical outcomes per trial for a multinomial probability distribution is three or more. The Option D.
How many categorical outcomes per trial does the distribution have?A multinomial probability distribution can have 3 or more categorical outcomes per trial. In a multinomial experiment, each trial results in one of several possible outcomes and the probabilities of these outcomes remain constant across multiple trials.
The outcomes are mutually exclusive and exhaustive meaning that only one outcome can occur in each trial and all possible outcomes are accounted for. Therefore, the number of categorical outcomes per trial for a multinomial probability distribution can be two or more.
Full question:
The number of categorical outcomes per trial for a multinomial probability distribution is
a. four or more.
b. three or more.
c. five or more.
d. two or more.
Read more about categorical outcomes
brainly.com/question/29670043
#SPJ4
Let A be a 4x4 matrix whose determinant is -3. Given that C24=93, determine the entry in the 4th row and 2nd column of A-1.
Answers
The entry in the 4th row and 2nd column of A⁻¹ is 4.
We can use the formula A × A⁻¹ = I to find the inverse matrix of A.
If we can find A⁻¹, we can also find the value in the 4th row and 2nd column of A⁻¹.
A matrix is said to be invertible if its determinant is not equal to zero.
In other words, if det(A) ≠ 0, then the inverse matrix of A exists.
Given that the determinant of A is -3, we can conclude that A is invertible.
Let's start with the formula: A × A⁻¹ = IHere, A is a 4x4 matrix. So, the identity matrix I will also be 4x4.
Let's represent A⁻¹ by B. Then we have, A × B = I, where A is the 4x4 matrix and B is the matrix we need to find.
We need to solve for B.
So, we can write this as B = A⁻¹.
Now, let's substitute the given values into the formula.We know that C24 = 93.
C24 represents the entry in the 2nd row and 4th column of matrix C. In other words, C24 represents the entry in the 4th row and 2nd column of matrix C⁻¹.
So, we can write:C24 = (C⁻¹)42 = 93 We need to find the value of (A⁻¹)42.
We can use the formula for finding the inverse of a matrix using determinants, cofactors, and adjugates.
Let's start by finding the adjugate matrix of A.
Adjugate matrix of A The adjugate matrix of A is the transpose of the matrix of cofactors of A.
In other words, we need to find the cofactor matrix of A and then take its transpose to get the adjugate matrix of A. Let's represent the cofactor matrix of A by C.
Then we have, adj(A) = CT. Here's how we can find the matrix of cofactors of A.
The matrix of cofactors of AThe matrix of cofactors of A is a 4x4 matrix in which each entry is the product of a sign and a minor.
The sign is determined by the position of the entry in the matrix.
The minor is the determinant of the 3x3 matrix obtained by deleting the row and column containing the entry.
Let's represent the matrix of cofactors of A by C.
Then we have, A = (−1)^(i+j) Mi,j . Here's how we can find the matrix of cofactors of A.
Now, we can find the adjugate matrix of A by taking the transpose of the matrix of cofactors of A.
The adjugate matrix of A is denoted by adj(A).adj(A) = CTNow, let's substitute the values of A, C, and det(A) into the formula to find the adjugate matrix of A.
adj(A) = CT
= [[31, 33, 18, -21], [-22, -3, 15, -12], [-13, 2, -9, 8], [-8, -5, 5, 4]]
Now, we can find the inverse of A using the formula
A⁻¹ = (1/det(A)) adj(A).A⁻¹
= (1/det(A)) adj(A)Here, det(A)
= -3. So, we have,
A⁻¹ = (-1/3) [[31, 33, 18, -21], [-22, -3, 15, -12], [-13, 2, -9, 8], [-8, -5, 5, 4]]
= [[-31/3, 22/3, 13/3, 8/3], [-33/3, 3/3, -2/3, 5/3], [-18/3, -15/3, 9/3, -5/3], [21/3, 12/3, -8/3, -4/3]]
So, the entry in the 4th row and 2nd column of A⁻¹ is 12/3 = 4.
Hence, the answer is 4.
To know more about invertible, visit:
https://brainly.in/question/8084703
#SPJ11
The entry in the 4th row and 2nd column of A⁻¹ is 32. Answer: 32
Given a 4x4 matrix, A whose determinant is -3 and C24 = 93, the entry in the 4th row and 2nd column of A⁻¹ is 32.
Let A be the 4x4 matrix whose determinant is -3. Also, let C24 = 93.
We are required to find the entry in the 4th row and 2nd column of A⁻¹. To do this, we use the following steps;
Firstly, we compute the cofactor of C24. This is given by
Cofactor of C24 = (-1)^(2 + 4) × det(A22) = (-1)^(6) × det(A22) = det(A22)
Hence, det(A22) = Cofactor of C24 = (-1)^(2 + 4) × C24 = -93.
Secondly, we compute the remaining cofactors for the first row.
C11 = (-1)^(1 + 1) × det(A11) = det(A11)
C12 = (-1)^(1 + 2) × det(A12) = -det(A12)
C13 = (-1)^(1 + 3) × det(A13) = det(A13)
C14 = (-1)^(1 + 4) × det(A14) = -det(A14)
Using the Laplace expansion along the first row, we have;
det(A) = C11A11 + C12A12 + C13A13 + C14A14
det(A) = A11C11 - A12C12 + A13C13 - A14C14
Where, det(A) = -3, A11 = -1, and C11 = det(A11).
Therefore, we have-3 = -1 × C11 - A12 × (-det(A12)) + det(A13) - A14 × (-det(A14))
The equation above impliesC11 - det(A12) + det(A13) - det(A14) = -3 ...(1)
Thirdly, we compute the cofactors of the remaining 3x3 matrices.
This leads to;C21 = (-1)^(2 + 1) × det(A21) = -det(A21)
C22 = (-1)^(2 + 2) × det(A22) = det(A22)
C23 = (-1)^(2 + 3) × det(A23) = -det(A23)
C24 = (-1)^(2 + 4) × det(A24) = det(A24)det(A22) = -93 (from step 1)
Using the Laplace expansion along the second column,
we have;
A⁻¹ = (1/det(A)) × [C12C21 - C11C22]
A⁻¹ = (1/-3) × [(-det(A12))(-det(A21)) - (det(A11))(-93)]
A⁻¹ = (-1/3) × [(-det(A12))(-det(A21)) + 93] ...(2)
Finally, we compute the product (-det(A12))(-det(A21)).
We use the Laplace expansion along the first column of the matrix A22.
We have;(-det(A12))(-det(A21)) = C11A11 = -det(A11) = -(-1) = 1.
Substituting the value obtained above into equation (2), we have;
A⁻¹ = (-1/3) × [1 + 93] = -32/3
Therefore, the entry in the 4th row and 2nd column of A⁻¹ is 32. Answer: 32
To know more about determinant, visit:
https://brainly.com/question/14405737
#SPJ11
You have two groups of 5 adults. In group 1, their ages are 35, 55, 75, 95, and 105. In group 2, their ages are 60, 61, 62, 63, and 64. Which group has a larger standard deviation
Answers
Group 1 has a larger standard deviation of 25.6 than Group 2 which has a standard deviation of 1.4.
Standard deviation is a statistical measure that calculates how far away each number in a set is from the mean and thus from every other number in the set.
Standard deviation is calculated as the square root of variance, where variance is the average of squared differences from the mean.
Let's compute the standard deviation of the two groups.
Group 1 has a mean of (35+55+75+95+105)/5=73
Age deviations from the mean (in years) are: -38, -18, +2, +22, +32
Squared deviations from the mean are: 1444, 324, 4, 484, 1024
Variance = (1444+324+4+484+1024)/5 = 654
Standard deviation = √(654) = 25.6
Group 2 has a mean of (60+61+62+63+64)/5=62.
Age deviations from the mean are: -2, -1, 0, +1, +2
Squared deviations from the mean are: 4, 1, 0, 1, 4
Variance = (4+1+0+1+4)/5 = 2
Standard deviation = √(2) = 1.4
Therefore, Group 1 has a larger standard deviation of 25.6 than Group 2 which has a standard deviation of 1.4.
To learn about standard deviation here:
https://brainly.com/question/24298037
#SPJ11
The square root of which of the following integers is between 7 and 8
Answers
Answer:
the square root of 50 and 60
Step-by-step explanation:
Answer:
Your answer would be the square root of 50 and 60.
Step-by-step explanation:
Hope I helped!!
2 1/4+2/5÷(−1/2)−1/4
Answers
Answer:
i believe its 1.2
Step-by-step explanation:
hopethishelpsya:)
The answer is 6/5.
When the numerator is always higher than or equal to the denominator, the fraction is said to be an improper fraction. When a fraction contains a whole number and a proper fraction is said to be a mixed fraction.
Write the given equation with mixed fraction to an improper fraction,
\(2\frac{1}{4}+\frac{2}{5}\div \left(\frac{-1}{2}\right)-\frac{1}{4}=\frac{9}{4}+\frac{2}{5}\div \left(\frac{-1}{2}\right)-\frac{1}{4}\)
When we divide a fraction, we convert division into multiplication by turning the fraction upside down. Here, we convert the division sign before (-1/2) into multiplication by changing this fraction upside down as (-2/1).
Therefore,
\(2\frac{1}{4}+\frac{2}{5}\div \left(\frac{-1}{2}\right)-\frac{1}{4}=\frac{9}{4}+\left(\frac{2}{5}\times\left(\frac{-2}{1}\right)\right)-\frac{1}{4}\)
Now using the BODMAS rule, solve the bracket first. Followed by multiplication, addition, and subtraction.
\(\begin{aligned}2\frac{1}{4}+\frac{2}{5}\div \left(\frac{-1}{2}\right)-\frac{1}{4}&=\frac{9}{4}-{\frac{4}{5}-\frac{1}{4}\\&=\frac{8}{4}-\frac{4}{5}\\&=\frac{40-16}{20}\\&=\frac{24}{20}\\&=\frac{6}{5}\end{aligned}\)
Therefore, the answer is 6/5.
To know more about the BODMAS rule:
https://brainly.com/question/17103671
The complete question is -
Simply the given expression 2 1/4+2/5÷(−1/2)−1/4
Find the missing length and area of each figure

Answers
LM = √(8² + 6²) = √(64 + 36) = √100 = 10 yd
Area = 2 × (1/2) × 6 × 8 = 48 yd²
A clothing designer determines that the number of shirts she can sell is given by the formula S = −4x2 + 80x − 76, where x is the price of the shirts in dollars. At what price will the designer sell the maximum number of shirts? a $324 b $19 c $10 d $1
Answers
To find the price at which the designer will sell the maximum number of shirts, we need to determine the vertex of the quadratic function representing the number of shirts sold.
The equation for the number of shirts sold is given by:
S = -4x^2 + 80x - 76
This is a quadratic function in the form of:
S = ax^2 + bx + c
To find the price at which the maximum number of shirts is sold, we need to locate the vertex of the quadratic function. The x-coordinate of the vertex can be found using the formula:
x = -b / (2a)
In this case, a = -4 and b = 80. Plugging in these values, we can calculate the x-coordinate:
x = -80 / (2*(-4))
x = -80 / (-8)
x = 10
Therefore, the designer will sell the maximum number of shirts at a price of $10. Hence, the correct option is c) $10.
HELPPPPPPPPPPPPPPPPPPPPp

Answers

Dianna made several loaves of bread yesterday. Each loaf required 2 and two-thirds cups of flour. All together, she used 13 and one-third cups of flour. How many loaves did Dianna make?
3 loaves
4 loaves
5 loaves
7 loaves
Answers
Answer:
5
Step-by-step explanation:
Answer:
5
Step-by-step explanation:
correct on eduinity
find the Area and Perimeter of the shaded figure Area = x squre unitsPerimeter = x units

Answers
Solution
We want to find the area and perimeter of the shaded figure.
The shape below is a rectangle
Therefore, the area of a rectangle is
\(\begin{gathered} A=L\times W \\ \text{ Where L is the length and W is the width} \end{gathered}\)while the perimeter of a rectangle is given by
\(P=2(L+W)\)Here, L = 2 unit and B = 3 units
\(A=2\text{ units}\times3\text{ units}=6\text{ square units}\)\(P=2(2+3)=2\times5=10\text{ units}\)Hence,
Area = 6 square units
Perimeter = 10 units
Please help me i will give you the brainlist crown  thanks!
( last word says parallelogram)

Answers
Answer:
77
Step-by-step explanation:
I am right for sure
to examine the effectiveness of two types of interventions for anxiety, researchers randomly assigned participants to a 12-week course of cognitive-behavioral therapy, a 12-week mindfulness-based stress reduction program, or a waitlist control group. the researchers administered a standardized measure of anxiety to participants before and after the interventions or waitlist period. in this experiment, what is the dependent variable?
Answers
The dependent variable in this experiment is the level of anxiety as measured by a standardized measure of anxiety before and after the interventions or waitlist period.
What is the dependent variable about?The dependent variable in this experiment is the standardized measure of anxiety that was administered to participants before and after the interventions or waitlist period.
The dependent variable is what is being measured or observed to determine the effectiveness of the two interventions (cognitive-behavioral therapy and mindfulness-based stress reduction program) for anxiety.
Therefore, The researchers are trying to find out how the interventions affect anxiety, so anxiety levels are the outcome or result of the intervention and therefore the dependent variable.
Learn more about dependent variable from
https://brainly.com/question/383055
#SPJ1
Name the quadrant or axis where the point (4.-6) is located.
Answers
Answer:
Step-by-step explanation:
(4, -6) is in quadrant IV , (quadrant 4)

Issac surveyed the employees at the law firm each employee was asked to record their highest level of education completed. Two hundred sixty six woolens completed the survey . How many of those people completed graduate school?
Answers
Complete Question :
Isaac surveyed the employees at a law firm. Each employee was asked to record their highest level of education completed. The
results are shown in the table below.
Highest Level of Education Completed
Education Level
Percentage
High School
5%
Community College
10%
Four-Year College
60%
Graduate School
25%
Two-hundred sixty people completed the survey. How many of those people completed graduate school?
Answer:
65 people
Step-by-step explanation:
Given the following :
Number of survey participants = 260
Percentage that completed graduate school = 25%
Number of participants who completed graduate school ;
Total Number of participants × percentage that completed graduate school
260 participants × 25%
260 × 0.25
= 65
Answer:
65 people
Step-by-step explanation:
I took the test and that was the correct answer
Simplify the expression. Write your answer as a power.
(-3)⁴/(-3)¹
The simplified expression is
Answers
Answer:
\((-3)^3\)
Step-by-step explanation:
\(\displaystyle \frac{(-3)^4}{(-3)^1}=(-3)^{4-1}=(-3)^3\)
If the simple interest on $5,000 for 9 years is $4,050, then what is the interest rate?
The rate is %?
Answers
Answer:
Total Interest Paid $432,400.00
Step-by-step explanation:
the imax screen at the michigan science center is 22 meters wide and 16.1 meters tall. what is diagonal length of the screen? use a calculator, do the work. round to nearest tenth of a meter. a 29.2 m b 743.2 m c 26.2 m d 27.2 m e 28.2 m
Answers
1) find c^2
22^2 + 16.1^2= c^2 ———->743.21
2) square root c^2 to find c
square root of 743.21 = 27.2 so D
A teacher is calculating the marks for the students in her Data Management class. She assigns the following values to each category. Knowledge: 25% Application: 20% Thinking: 10% Culminating Project: 15% Final Exam: 15% Communication: 15% Kyle has not yet written his final exam, but his marks in the first five categories are 90, 79, 82, 70, and 85. a) Determine the weighted mean for Kyle before the final exam. b) How does this weighted mean differ from the unweighted mean?
Answers
Weighted Mean = (90 × 25% + 79 × 20% + 82 × 10% + 70 × 15% + 85 × 15%) / (25% + 20% + 10% + 15% + 15%)
Unweighted Mean = (90 + 79 + 82 + 70 + 85) / 5
One student, Kyle, hasn't taken his final exam yet, but his marks in the first five categories are 90, 79, 82, 70, and 85. This problem requires determining the weighted mean for Kyle before the final exam and comparing it to the unweighted mean.
To calculate the weighted mean for Kyle before the final exam, we need to multiply each category's mark by its corresponding weight, sum them up, and divide by the total weight. For Kyle, the weighted mean would be calculated as follows:
Weighted Mean = (Knowledge × 25% + Application × 20% + Thinking × 10% + Culminating Project × 15% + Final Exam × 15% + Communication × 15%) / (Total Weight)
However, since Kyle hasn't written his final exam yet, we can exclude the Final Exam mark and its weight from the calculation. The weighted mean would then be:
Weighted Mean = (90 × 25% + 79 × 20% + 82 × 10% + 70 × 15% + 85 × 15%) / (25% + 20% + 10% + 15% + 15%)
To find the difference between the weighted mean and the unweighted mean, we need to calculate the unweighted mean by simply taking the average of the marks in the first five categories:
Unweighted Mean = (90 + 79 + 82 + 70 + 85) / 5
By comparing the weighted mean and the unweighted mean, we can evaluate how much the inclusion of weights for different categories affects Kyle's overall mark.
For more information on weighted Mean visit: brainly.com/question/14521450
#SPJ11
solve for x and round please

Answers
Answer:
9.6
Step-by-step explanation:
6.4/x = sin42
x = 6.4/sin42
x = 9.56
Another famous puzzle used as an example in the study of artificial intelligence seems first to have appeared in a collection of problems, Problems for the Quickening of the Mind, which was compiled about A.D. 775. It involves a wolf, a goat, a bag of cabbage, and a ferryman. From an initial position on the left bank of a river, the ferryman is to transport the wolf, the goat, and the cabbage to the right bank. The difficulty is that the ferryman’s boat is only big enough for him to transport one object at a time, other than himself. Yet, for obvious reasons, the wolf cannot be left alone with the goat, and the goat cannot be left alone with the cabbage. How should the ferryman proceed?
Answers
The ferryman should transport the goat first, then return alone to bring the wolf, leaving the goat on the right bank. Finally, he should transport the cabbage and leave it with the wolf.
In order to solve this puzzle, the ferryman must make a series of careful moves to ensure the safety of the wolf, goat, and cabbage. The first step is to transport the goat to the right bank, leaving it there. The ferryman then returns to the left bank alone.
He takes the wolf across the river, but before leaving it on the right bank, he brings the goat back to the left bank. Now, the goat and cabbage are on the same side, while the wolf remains on the right bank.
The ferryman transports the cabbage to the right bank, leaving it there, and then returns alone to the left bank. Finally, he takes the goat across the river one last time, completing the puzzle. This sequence of moves ensures that the wolf and goat are never left alone together, nor are the goat and cabbage.
for such more questions on transport
https://brainly.com/question/21287562
#SPJ8
You meet two students in the library. At least one of them is an upperclassman who is currently taking EECS 126. Assume each student is an upperclassmen and underclassmen with equal probability and each student takes 126 with probability 1 10 , independent of each other and independent of their class standing. What is the probability that both students are upperclassmen
Answers
There is a 50% chance that both students are upperclassmen.
Given: Two students meet at a library, where at least one of them is an upperclassman who is currently taking EECS 126, assume each student is an upperclassman and underclassmen with equal probability and each student takes 126 with probability 1/10, independent of each other and independent of their class standing. To find: Probability that both students are upperclassmen.
Solution: Let P(A) be the probability that a student is an upperclassman, and P(B) be the probability that a student is taking EECS 126.P(A) = 1/2 (Given, Assume each student is an upperclassman and underclassmen with equal probability) P(B) = 1/10 (Given, each student takes 126 with probability 1/10, independent of each other and independent of their class standing) Let C be the event that both students are upperclassmen. Then, P(C) = Probability that both students are upperclassmen P(C') = Probability that one student is an underclassman or both are underclassmen P(C') = P(Ac) ...(i) P(C') = 1 - P(C) ...(ii) P(Ac) = P(underclassman) = 1/2 (Given, Assume each student is an upperclassman and underclassmen with equal probability)
Now, P(C') = P(Ac) = 1/2 ...from (i) P(C) = 1 - P(C') = 1 - 1/2 = 1/2 Also, P(B) and P(A) are independent events as given in the question, So, P(AB) = P(A)P(B) = (1/2) x (1/10) = 1/20 Hence, the probability that both students are upperclassmen is P(AB) = 1/20.In other words, there is a 50% chance that both students are upperclassmen.
Know more about Probability here:
https://brainly.com/question/32900629
#SPJ11
One number is nine more than another number.if the sum of the number is 65 ,find both numbers
Answers
Answer:
The first number is 28 the number nine more is 37
Hope this helped!
how many squares of side 5 cm are required to cover a rectangle measuring 35 cm by 20 cm?
Answers
1.) Area of a square:
A=s^2
A=(5)^2
A=25cm^2.
The area of the square is 25cm^2.
2.) Area of the rectangle:
A=L•W
A=(35)•(20)
A=700cm^2.
Therefore, the area of the rectangle is 700cm^2.
Now, we must create an Algebraic equation to figure out how many times the area of the square will fit into the area of the rectangle.
4.) 25X=700.
25X/25=700/25
X=28
We know one square with side lengths of 5 is 25, and we are trying to figure out how many times the area of the square will equally fit into the area of the rectangle. X=factor of how many the area of the square is multiplied to total the area of the rectangle.
Therefore, the square will fit into the rectangle 28 times, so there are 28 squares with the same dimensions that will fit into the rectangle.
Answer:
28 squares of 5cm x 5 cm (25cm^ each)
Step-by-step explanation:
35/5 = 7 sides measuring 5 cm each. (Length divided in 7)
20/5 = 4 sides measuring 5 cm each (width divided in 4)
7 x 4 = 28 squares of 5 x 5