On a map, 2 inches represents 350 miles. If the distance between 2 cities
is 875 miles, how many inches apart are they on the map?
Answers
Answer:
5 INCHES
Step-by-step explanation:
If 2 inches = 350 miles
then 1 inch is 350%2 which is 175
So 875 % 175 = 5 inches
Related Questions
9. Determine algebraically where the cubic function with zeros at 2, 3 and -5 and passes through the point (4, 36) has a value of 120. (4 marks)
Answers
At x = 8, the cubic function has a value of 120.
Given that the cubic function has zeros at 2, 3, and -5, then its factors must be (x - 2), (x - 3), and (x + 5).
Therefore, the cubic function can be expressed in the factored form as:
=> f(x) = k(x - 2)(x - 3)(x + 5) ; where k is a constant.
Since f(x) passes through the point (4, 36), we can substitute x = 4 and f(x) = 36 in the above equation to get:
=> 36 = k(4 - 2)(4 - 3)(4 + 5)
=> 36 = k(2)(1)(9)
=> 36 = 18k
=> k = 2
So, the cubic function can be expressed as:
=> f(x) = 2(x - 2)(x - 3)(x + 5)
Now we can find where f(x) has a value of 120 by solving for x:
=> 120 = 2(x - 2)(x - 3)(x + 5)
=> 60 = (x - 2)(x - 3)(x + 5)
Since 2 is a factor of the left-hand side, then we know that one of the factors on the right-hand side must be 2. Therefore, we can write:
=> 60 = 2(x - 2)(x - 3)(x + 5)
=> 30 = (x - 2)(x - 3)(x + 5)
Now we can use trial and error method to find the other two factors that multiply to 30. We can start with (x - 2) = 1, (x - 3) = 5, and (x + 5) = 6. This gives us: x = 3, 8, -11
However, only x = 8 satisfies the condition that f(x) = 120, so the cubic function has a value of 120 at x = 8.
Thus, at x = 8, the cubic function has a value of 120.
Learn more about cubic functions:
https://brainly.com/question/29640289
#SPJ11
Frahan travels from Town A to Town B at an average speed of 4 Km/h and from Town B to Town A at an average
speed of 3 Km/h. He takes 25 minutes to complete the entire journey.
(a) Convert 25 minutes into hours.
(b) Find his total distance travelled.
Answers
to convert 25min into hours we divide 25 by 60 so the answer would be 0.416 hours
the formula to find the distance is we multiply speed and time so
distance=4km/p X 0.416 hours =1.664
so now we have the first answer
now we do the same thing for the other part of the question
distance= timeXspeed
distance=0.416X3=1.248
then we add to find total distance
1.248+1.644=2.912
2.912 is the total distance
Determine the value of x in the following triangle.

Answers
Answer:
the value of x is 9
Step-by-step explanation:
the sum of all angles of a triangle is 180
one side is 90 so,
90+7x+3x = 180
10x = 180-90
10x = 90
x=9
Need to find the Domain and Range

Answers
Answer:
D: {x∈R | -2 ≤ x ≤ 2 }
R: {y∈R | 0 ≤ y ≤ 4 }
Step-by-step explanation:
The domain ranges between -2 and 2
The range ranges between 0 and 4
show all work please

Answers
Answer:
please I can see the questions well
Step-by-step explanation:
please I want to help you but
the picture is not clear enough
A boat sails 40 miles south and then 30 miles east. How far is the boat from its starting point?
Answers
Answer:
50 miles
Step-by-step explanation:
A receptionist can type documents 4 times as fast as her assistant. Working together, they can type up a day's worth of documents in 3
hours. On a day that the assistant is absent from work, find the number of hours, n. that it will take the receptionist to type up the day's
documents on her own.
Answers
Answer:
3.75 hours
Step-by-step explanation:
The receptionist takes n hours to do 1 day's worth of work.
The assistant takes 4n hours to the 1 day's worth of work.
In 1 hour, the receptionist does 1/n amount of work.
In 1 hour, the assistant does 1/(4n) amount of work.
Working together, in 1 hour, they do this amount of work:
1/n + 1/(4n)
Working together, the 2 workers do the job in 3 hours.
Working together, in 1 hour, they do this amount of work:
1/3
1/n + 1/(4n) = 1/3
Multiply both sides of the equation by the LCD, 12n.
12 + 3 = 4n
4n = 15
n = 15/4
n = 3.75
Answer: 3.75 hours
Find the mean of the following numbers:
12
1
10
9
3
4
9
7
9
Answers
Answer:
7.11
Step-by-step explanation:
You will add all of those numbers and divide them by the amount of numbers you added. And I rounded the answer to 2 decimal places, seeing that it is a recurring decimal.
Find the center and radius of the circle with the equation x^2 + y^2 = 9. Then graph the circle.

Answers
Answer:
center = origin (0,0)
radius = 3
to graph it, draw a circle that goes through the points (3,0), (0,3), (-3,0), (0,-3)
Step-by-step explanation:
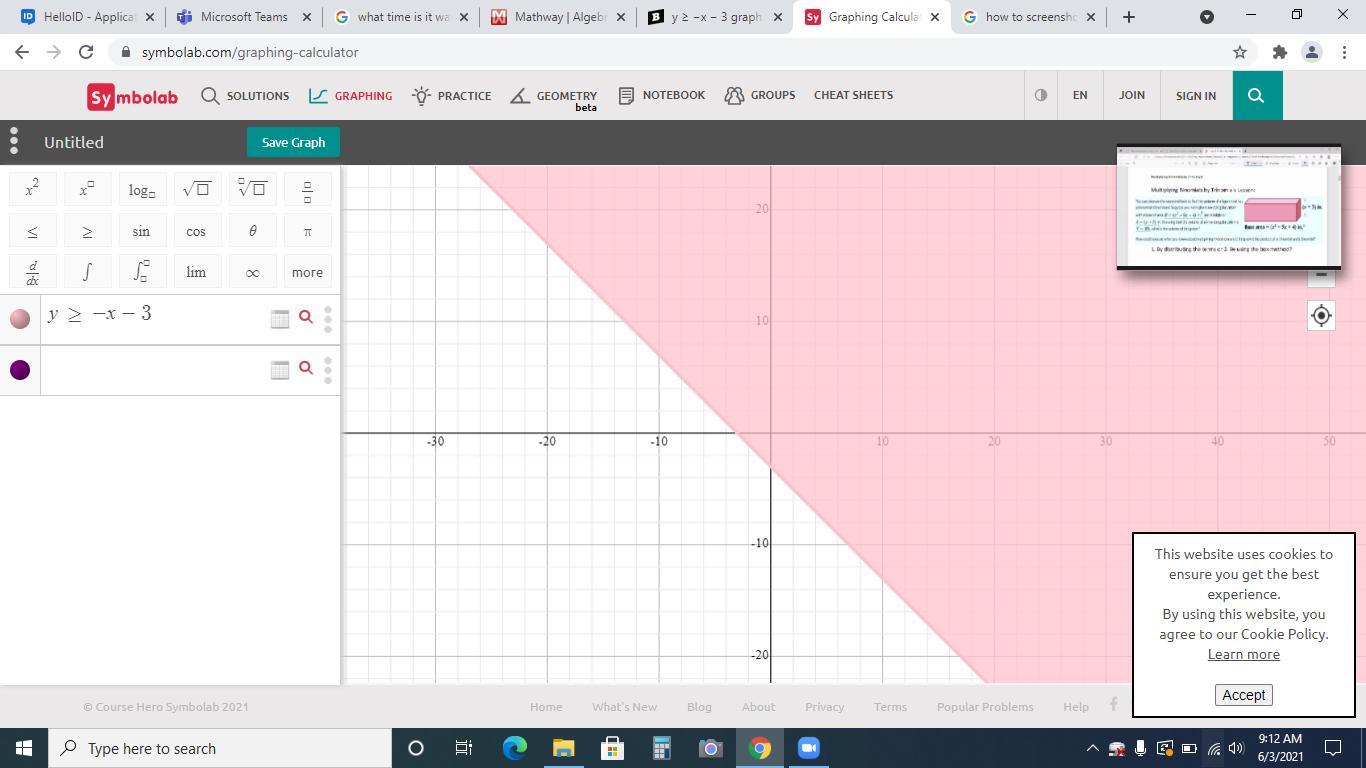
y ≥ −x − 3 graph the question
Answers
Answer:
Step-by-step explanation:
Have a Nice Day

Answer:
Step-by-step explanation:
20 POINTS ILL MARK U BRAINLIEST PLS

Answers
Answer:
13 + \(\sqrt{89}\)
or
22.43398... (depends on how you round it)
Step-by-step explanation:
1. The question stated that the radius of the circle O is 5, so the length of AO and CO is 5.
2. Since line AB and line CB are both tangent to the circle, they have the same length. CB is 8, so AB will also be 8.
--> Both triangle AOB and COB share one side, and the other side (radius) has the same length, so the third side must be the same length
3. Tangent means having a 90-degree angle with the radius. We know that the triangle AOB is a right triangle since the angle OAB is 90 degrees.
We can use the Pythagorean theorem to find side OB. OB^2 = AO^2 + AB^2.
--> OB^2 = 25 + 64
--> OB^2 = 89
--> OB = \(\sqrt{89}\)
Now that we know the lengths of all three sides, we can add them up.
--> 5 + 8 + \(\sqrt{89}\)
--> 13 + \(\sqrt{89}\)
or
--> 22.43398113....
If y=1-x+6x^(2)+3e^(x) is a solution of a homogeneous linear fourth order differential equation with constant coefficients, then what are the roots of the auxiliary equation?
Answers
The roots of the auxiliary equation are 0 (repeated root) and -b, where b is a constant.
To find the roots of the auxiliary equation for a homogeneous linear fourth-order differential equation with constant coefficients, we need to substitute the given solution into the differential equation and solve for the roots.
The given solution is: \(y = 1 - x + 6x^2 + 3e^x.\)
The general form of a fourth-order homogeneous linear differential equation with constant coefficients is:
ay'''' + by''' + cy'' + dy' + ey = 0.
Let's differentiate y with respect to x to find the first and second derivatives:
\(y' = -1 + 12x + 3e^x,\)
\(y'' = 12 + 3e^x,\)
\(y''' = 3e^x,\)
\(y'''' = 3e^x.\)
Now, substitute these derivatives into the differential equation:
\(a(3e^x) + b(3e^x) + c(12 + 3e^x) + d(-1 + 12x + 3e^x) + e(1 - x + 6x^2 + 3e^x) = 0.\)
Simplifying the equation, we get:
\(3ae^x + 3be^x + 12c + 3ce^x - d + 12dx + 3de^x + e - ex + 6ex^2 + 3e^x = 0.\)
Rearranging the terms, we have:
\((6ex^2 + (12d - e)x + (3a + 3b + 12c + 3d + 3e))e^x + (12c - d + e) = 0.\)
For this equation to hold true for all x, the coefficients of each term must be zero. Therefore, we have the following equations:
6e = 0 ---> e = 0,
12d - e = 0 ---> d = 0,
3a + 3b + 12c + 3d + 3e = 0 ---> a + b + 4c = 0,
12c - d + e = 0 ---> c - e = 0.
From the equations e = 0 and d = 0, we can deduce that the differential equation has a repeated root of 0.
Substituting e = 0 into the equation c - e = 0, we get c = 0.
Finally, substituting d = 0 and c = 0 into the equation a + b + 4c = 0, we have a + b = 0, which implies a = -b.
Therefore, the roots of the auxiliary equation are 0 (repeated root) and -b, where b is a constant.
To know more about auxiliary equation refer here:
https://brainly.com/question/18521479
#SPJ11
Which transformation were applied to the graph of the parent function y=tan(x) to produce the function graphed below?
Answers
Answer:d. a horizontal stretch to produce a period of 3pi/2 and a horizontal translation of pi/4 units to the right
Step-by-step explanation:
:)
Answer:
A horizontal stretch to produce a period of 3pi/2 and a horizontal translation of pi/4 units to the right
Step-by-step explanation:
While there's not graph provided, I've taken the test a little while ago and it seem to be right.
HELP ASAP THANK YOU!)
In order to hang a block of gold from a chain necklace, a jeweler drilled a hole in the center, 5 mm in diameter the original block of gold.
If the original block of gold was 27 mm long, 8 mm wide, and 12 mm high, find the volume of the remaining piece of gold to the nearest tenth cubic millimeter.
(The answer choices are below)

Answers
Answer:
2061.9\(mm^{3}\)
Step-by-step explanation:
We can see the original shape of the gold block is a cuboid.
Volume of Cuboid = Length x Width x Height
Volume of Original Gold Block = 27mm x 8mm x 12mm = \(2592mm^{3}\)
Next, we can see the shape of the cut-out hole is a cylinder.
Volume of Cylinder = \(\pi r^{2} h\)
We know that r = 0.5 x diameter = 0.5 x 5 = 2.5mm
Volume of cut-out hole = \(\pi (2.5)^{2} (27)\\\) = \(168.75\pi mm^{3}\)
Volume of Remaining Gold Block = Volume of Original Gold block - Volume of cut-out hole
= \(2592mm^{3} -168.75\pi mm^{3}\)
= 2061.9\(mm^{3}\)
If a figure is dilated by a factor of 6, the area of the figure will change by a factor of?
Answers
Answer:
36
Step-by-step explanation:
Given the scale factor k, then
the area factor is k²
Here the scale factor = 6 thus
area factor = 6² = 36
Identify equations, expressions, and inequalities
Identify whether each phrase is an expression, equation, or inequality.
HUH PLEASE HELP

Answers
Answer:
the middle one goes to the top, top one goes to the middle and bottom stays there
Step-by-step explanation:
Lena has 1.6 kg of sugar. She uses 470 g for a cake. How much sugar does she have left? Give your answer in g.
Answers
Answer:
1130 grams
Step-by-step explanation:
1.6kg to grams is 160 0grams so 1600 - 470 = 1130 so she has 1130 grams left.
Answer:
Lena has 1130 grams left.
1.6 kg = 1600 grams
Amount of sugar she used = 470 grams
Amount of sugar she has left = 1600 - 470
= 1130 grams
So, Lena has 1130 grams of sugar left.
:)
32. A student finds the slope of the line between (4, 12) and (4, 17) . She writes 12-17 4-4 , What mistake did she make?
Answers
Please help on timer ill give 15 brainlist

Answers
Answer:
B
Step-by-step explanation:
A polling company has decided to increase the size of its random sample of voters from about 1,000 people to about 2,800 people right before an election. A poll was designed to estimate the proportion of voters who favor a new law banning cell phone use in Internet coffee shops. What is the effect of this increase
Answers
Increasing the sample size from 1,000 to 2,800 will improve the accuracy and precision of the poll's estimate, providing a more reliable measurement of the proportion of voters who favor the new law banning cell phone use in Internet coffee shops.
We have,
Increasing the size of the random sample from about 1,000 people to about 2,800 people will have a positive effect on the accuracy and precision of the poll's estimate.
When conducting a poll, the sample size is an important factor in determining the reliability of the results.
A larger sample size generally leads to more accurate estimates and reduced sampling error.
By increasing the sample size from 1,000 to 2,800, the polling company is effectively collecting data from a larger and more diverse group of voters.
This larger sample size allows for a better representation of the population, reducing the potential for bias and increasing the reliability of the estimate.
With a larger sample size, the margin of error of the poll is likely to decrease.
The margin of error represents the range within which the true population proportion is likely to fall.
Increasing the sample size reduces the variability of the estimates and narrows the range of the margin of error.
Thus,
Increasing the sample size from 1,000 to 2,800 will improve the accuracy and precision of the poll's estimate.
Learn more about random samples here:
https://brainly.com/question/30759604
#SPJ12
Given that ABCD is a rectangle, where EC = 7x -5 and AE = 3x+ 9. Find DE.

Answers
Answer:
DE = 19.5
Step-by-step explanation:
the diagonals of a rectangle are congruent and bisect each other, then
EC = AE , that is
7x - 5 = 3x + 9 ( subtract 3x from both sides )
4x - 5 = 9 ( add 5 to both sides )
4x = 14 ( divide both sides by 4 )
x = 3.5
Then
AE = 3x + 9 = 3(3.5) + 9 = 10.5 + 9 = 19.5
Thus
DE = AE = 19.5
a collection of field goal kickers are divided into groups 1 and 2. group i has 3i kickers. on any kick, a kicker from group i will kick a field goal with probability 1/(i + 1), independent of the outcome of any other kicks
Answers
The probability that a kicker from group i will make a field goal is 1/(i + 1), where i represents the group number.
In the given scenario, the field goal kickers are divided into two groups: group 1 and group 2. Each group has 3i kickers, where i represents the group number.
The probability that a kicker from group i will make a field goal is given by 1/(i + 1). This means that the probability of a successful field goal attempt for a kicker in group 1 is 1/2, and for a kicker in group 2 is 1/3.
The probability of making a field goal is independent of the outcome of any other kicks, meaning that the success or failure of one kicker's attempt does not affect the probability of success for another kicker.
In the collection of field goal kickers divided into groups 1 and 2, the probability of a kicker from group i successfully making a field goal is 1/(i + 1), where i represents the group number. The success or failure of one kicker's attempt does not impact the probability of success for another kicker.
To know more about probability , Visit:
https://brainly.com/question/23417919
#SPJ11
What would be the volume (in cubic centimeters) of such a bacterium, assuming that it is spherical? Express your answer in cubic centimeters. Part B What would be the surface area (in square millimeters) of such a bacterium, assuming that it is spherical? Express your answer in square millimeters. What would be the volume (in cubic centimeters) of such a bacterium, assuming that it is spherical? Express your answer in cubic centimeters. Part B What would be the surface area (in square millimeters) of such a bacterium, assuming that it is spherical? Express your answer in square millimeters. Bacteria vary somewhat in size, but a diameter of 2.9 μm is not unusual.
Answers
The surface area of the bacterium is approximately 2.64 × 10⁻⁷ mm². The volume of the bacterium is approximately 1.43 × 10⁻³³ cm³ .
To find the volume of a spherical bacterium, we can use the formula for the volume of a sphere: V = (4/3)πr³, where r is the radius of the bacterium. Given that the diameter of the bacterium is 2.9 μm, we can calculate the radius by dividing the diameter by 2: r = 2.9 μm / 2 = 1.45 μm.
Converting the radius to centimeters, we divide by 10,000 (since 1 cm = 10,000 μm): r = 1.45 μm / 10,000 = 0.000145 cm.
Now we can substitute the radius into the volume formula: V = (4/3)π(0.000145 cm)³.
Evaluating the expression, the volume of the bacterium is approximately 1.43 × 10⁻³³ cm³ .
To find the surface area of the bacterium, we use the formula for the surface area of a sphere: A = 4πr².
Substituting the radius into the formula, we get: A = 4π(0.000145 cm)².
Evaluating the expression, the surface area of the bacterium is approximately 2.64 × 10⁻⁷ mm².
Learn more about volume here:
brainly.com/question/10167786
#SPJ11
Calcula la masa y el peso específico de 1500 litros de gasolina
Answers
The mass of 1500 liters of gasoline is 1110 grams, and the specific weight is approximately 0.007252 g/cm³.
To calculate the mass of 1500 liters of gasoline, we need to know the density of gasoline. The density of gasoline is typically around 0.74 grams per milliliter. Since there are 1000 milliliters in a liter, we can convert the volume to milliliters by multiplying 1500 liters by 1000, which gives us 1,500,000 milliliters. Then, we can calculate the mass by multiplying the volume in milliliters by the density, which gives us 1,500,000 milliliters * 0.74 grams per milliliter = 1,110,000 grams or 1110 kg.
The weight-specific or specific weight of a substance is the weight per unit volume. It can be calculated by multiplying the density of the substance by the acceleration due to gravity. In the case of gasoline, the specific weight would be approximately 0.74 grams per milliliter * 9.8 m/s² = 0.007252 g/cm³.
Learn more about liters of gasoline here:
https://brainly.com/question/28274982
#SPJ11
farmer bob needs to build a fence for his chicken's. the space he wants to build a fence around is 40 feet long and 20 feet wide.how many feet of fence he needs to buy
Answers
Answer:
120 feet
Step-by-step explanation:
You would find the perimeter of the fence, which is 40(2) + 20(2)
chapter 7.1.6 puzzle core connections algebra

Answers
The exponential function is y = 1200(1.04)^t and the investment amount after 16 years is $2247.58.
What is exponential function?
The formula for an exponential function is f(x) = a^x, where x is a variable and a is a constant that serves as the function's base and must be bigger than 0.
Jayden invests $1,200 in a savings account. Each year, the value increases by 4%.
Let t = time in years
Let y = amount of money invested in savings account
Start with $1200 and each year add 4% interest to the amount in the bank.
1st year: Interest = 1200 × (0.04) = $48
This is added to the previous amount -
= $1200 + $1200 × (0.04)
= $1200 (1+0.04)
= $1200 (1.04)
= $1248
2nd year: Previous amount + interest on the previous amount
= $1248 (1+0.06)
= $1248 (1.06)
= $1297.92
So, the exponential formula becomes -
y = 1200(1.04)^t
Now, to find the value of investment after 16 years, substitute t = 16.
y = 1200(1.04)^t
y = 1200(1.04)^16
y = 1200(1.87298125)
y =$2247.58
Therefore, the value of investment after 16 years is $2247.58.
To learn more about exponential function from the given link
https://brainly.com/question/11464095
#SPJ1
The given figure of a solid made up of cylinder and a cone. If the diameter of the cylinder is 12 cm , height 80 cm ,the slant height of the cone is 10 cm , find the total surface area of the solid object.

Answers
Answer:
\(\huge\boxed{\sf 3317.5\ cm\²}\)
Step-by-step explanation:
Since the diameter is 12 cm, the radius will be:
r = d/2 = 12/2 = 6 cm
Now,
Surface Area of cylinder:
\(= 2\pi rh+2\pi r^2\\\\Where \ r = 6 \ cm, \ h = 80 \ cm\\\\= 2(3.14)(6)(80)+2(3.14)(6)^2\\\\= 3015.9+2(3.14)(36)\\\\= 3242.12 \ cm^2\)
Surface Area of Cone:
\(= \pi r^2+\pi rl\\\\Where \ r = 6 \ cm, \ l = 10 \ cm\\\\= (3.14)(6)^2+(3.14)(6)(10)\\\\= (3.14)(36)+188.5\\\\= 113.1+188.5\\\\= 301.6 \ cm^2\)
Surface area of the object:
= SA of cone + SA of cylinder - 2πr² (Since the base area isn't included)
= 301.6 + 3242.1 - 2(3.14)(6)²
= 3543.7 - 2(3.14)(36)
= 3543.7 - 226.2
= 3317.5 cm²
\(\rule[225]{225}{2}\)
Hope this helped!
~AH1807the total surface area of the solid object is \(\bold{\green{1056\pi\: Or\:3317.52\:cm^2}}\)
Answer:
Solution given:
diameter [d]=12 cm
radius [r]=\(\frac{12}{2}=6\) cm
height of cylinder[H]=80cm
slant height [L]=10cm
Now,
Surface Area of cylinder=\(2\pi rH\)
=\(2\pi *6*80=960\pi cm^2\)
Surface Area of Cone:\(\pi rL\)
=\(\pi *6*10=60\pi cm^2\)
Surface area Base of solid=\(\pi r^2=\pi *6^2=36\pi cm^2\)
The total surface area of the object:
=Surface Area of cylinder + Surface Area of Cone+ Surface area Base of solid
=\(960\pi +60\pi +36\pi\)
=\(1056\pi\: Or\:3317.52\:cm^2\)
Step-by-step explanation:

Suppose that grade point averages of undergraduate students at one university have a bell-shaped distribution with a mean of 2.56 and a standard deviation of 0.45. Using the empirical rule, what percentage of the students have grade point averages that are greater than 1.66
Answers
Using the empirical rule, we can estimate that approximately 97.5% of the students have GPAs that are greater than 1.66 at this university.
The empirical rule, also known as the 68-95-99.7 rule, states that for a normal distribution, approximately 68% of the data falls within one standard deviation of the mean, 95% falls within two standard deviations, and 99.7% falls within three standard deviations.
To apply this rule to the given scenario, we first need to calculate how many standard deviations away from the mean a GPA of 1.66 is.
Z = (X - μ) / σ
Where X is the GPA in question, μ is the mean (2.56), and σ is the standard deviation (0.45).
Z = (1.66 - 2.56) / 0.45 = -2
This tells us that a GPA of 1.66 is 2 standard deviations below the mean.
Now, using the empirical rule, we know that approximately 95% of the data falls within two standard deviations of the mean. Since a GPA of 1.66 is 2 standard deviations below the mean, we can conclude that only about 2.5% (half of the remaining 5%) of the students have a GPA lower than 1.66.
Therefore, the percentage of students who have GPAs that are greater than 1.66 would be approximately 97.5%.
To know more about empirical rule, refer to the link below:
https://brainly.com/question/18025920#
#SPJ11
Compare the two groups of data. which statement is true?

Answers
The true statement is the range of Mrs Plum's class is 14 greater than the range of Mr Scarlet's class.
What is the range?A box plot is a graph that is used to describe a dataset. A box plot is made up of two lines and a box. The two lines are known as whiskers.
The end of the first whisker represents the minimum number and the end of the second whisker represents the maximum number. The difference between the whiskers is the range.
Range is used to measure the variation of a dataset. It is the difference between the maximum number and the minimum number.
Range = maximum number - minimum number
Range of Miss Scarlet's class = 98 - 65 = 33
Range of Miss Plum's class = 98 - 51 = 47
Difference in range = 47 - 33 = 14
To learn more about box plots, please check: https://brainly.com/question/27215146
#SPJ1
One year Ted had the lowest ERA (earned-run average, mean number of runs yielded per nine innings pitched) of any male pitcher at his school, with an ERA of 2.78. Also, Julie had the lowest ERA of any female pitcher at the school with an ERA of 2.84. For the males, the mean ERA was 4.767 and the standard deviation was 0.859. For the females, the mean ERA was 3.866 and the standard deviation was 0.937. Find their respective Z-scores. Which player had the better year relative to their peers, Ted or Julie? (Note: In general, the lower the ERA, the better the pitcher.) Ted had an ERA with a z-score of Julie had an ERA with a z-score of (Round to two decimal places as needed.) Which player had a better year in comparison with their peers? A. Julie had a better year because of a lower z-score. B. Julie had a better year because of a higher z-score. C. Ted had a better year because of a higher z-score. D. Ted had a better year because of a lower z-score.
Answers
The correct answer is D. Ted had a better year because of a lower z-score.
The following formula can be used to determine Ted and Julie's respective z-scores:
z = (x - )/, where:
x is the individual's ERA, the mean ERA for each group, and the standard deviation of the ERA for each group.
To Ted:
x (Ted's ERA) = 2.78; the mean ERA for males is 4.767; the standard deviation for males is 0.859. Regarding Julie:
The z-scores were calculated as follows: x (Julie's ERA) = 2.84 (mean ERA for females) = 3.866 (standard deviation for females) = 0.937
z (Ted) = (2.78 - 4.767) / 0.859 -2.32 z (Julie) = (2.84 - 3.866) / 0.937 -1.09 Add two decimal places to the z-scores.
Ted's z-score is lower (-2.32) when compared to Julie's (-1.09) when the z-scores are compared.
A person's value (ERA) is further below the mean when compared to their peers if their z-score is lower. As a result, Ted outperformed Julie in comparison to his peers.
The right response is D. Ted had a superior year in view of a lower z-score.
To know more about Z-score, visit
brainly.com/question/25638875
#SPJ11