Nolan ordered a set of beads. He received 86 beads in all. 43 of the beads were orange. What percentage of the beads were orange?
Answers
50% of the beads Nolan received were orange.
To find the percentage of beads that were orange, we need to divide the number of orange beads by the total number of beads and then multiply by 100.
Percentage of orange beads = (Number of orange beads / Total number of beads) * 100
In this case, Nolan received a total of 86 beads, and 43 of them were orange.
Percentage of orange beads = (43 / 86) * 100
Calculating this expression:
Percentage of orange beads = 0.5 * 100
Percentage of orange beads = 50%
Therefore, Out of total number of beads Nolan received, 50% were orange.
To learn more about percentage
https://brainly.com/question/31654195
#SPJ11
Related Questions
the base of a triangle is shrinking at a rate of 2 cm/min and the height of the triangle is increasing at a rate of 3 cm/min. find the rate (in cm2/min) at which the area of the triangle changes when the height is 38 cm and the base is 32 cm.
Answers
When the height is 38 cm and the base is 32 cm, the rate at which the area of the triangle changes is 10 cm²/min.
The rate at which the area of a triangle changes can be found by multiplying the rate at which the base is shrinking by the rate at which the height is increasing.
Given:
Rate of shrinking of the base = -2 cm/min
Rate of increasing of the height = 3 cm/min
Height of the triangle = 38 cm
Base of the triangle = 32 cm
To find the rate at which the area of the triangle changes, we use the formula for the area of a triangle:
Area = (1/2) * base * height
Differentiating the area formula with respect to time gives us:
dA/dt = (1/2) * (db/dt) * height + (1/2) * base * (dh/dt)
Substituting the given values, we have:
dA/dt = (1/2) * (-2) * 38 + (1/2) * 32 * 3
Simplifying, we get:
dA/dt = -38 + 48
dA/dt = 10 cm²/min
Therefore, when the height is 38 cm and the base is 32 cm, the rate at which the area of the triangle changes is 10 cm²/min.
To know more about triangle refer here:
https://brainly.com/question/2773823
#SPJ11
Find the domain of the logarithmic function. (Enter your answer using interval notation.) f(x) = -log3(x + 3) Find the x-intercept. (x, y) = Find the vertical asymptote. x =
Answers
To find the domain of the logarithmic function f(x) = -log3(x + 3), we first need to identify the values of x for which the function is defined. Logarithmic functions are defined only for positive arguments, meaning that we need x + 3 > 0.
Step 1: Solve the inequality x + 3 > 0.
x > -3
The domain of the function is all x values greater than -3. In interval notation, this is written as (-3, ∞).
Now, let's find the x-intercept of the function, which is the point where the function crosses the x-axis (y = 0). To do this, we need to solve the equation f(x) = 0 for x.
Step 2: Set f(x) = 0 and solve for x.
0 = -log3(x + 3)
-log3(x + 3) = 0
Step 3: Solve for the logarithmic equation.
log3(x + 3) = 1
Step 4: Rewrite the logarithmic equation in exponential form.
3^1 = x + 3
3 = x + 3
Step 5: Solve for x.
x = 3 - 3
x = 0
The x-intercept is (0, 0).
Lastly, let's find the vertical asymptote of the function. This is the line that the function approaches but never actually reaches. For logarithmic functions, the vertical asymptote is located at the point where the argument of the log is zero.
Step 6: Set x + 3 = 0 and solve for x.
x = -3
The vertical asymptote is x = -3.
To summarize:
- Domain: (-3, ∞)
- X-intercept: (0, 0)
- Vertical asymptote: x = -3
To learn more about ''domain of the logarithmic function'' visit : https://brainly.com/question/16444481
#SPJ11
you need to split it in half then multply then add

Answers
Answer:
130^2 or 130 meters squared
Step-by-step explanation:
I decomposed the figure, then found the area of the decomposed figures then found the sum of them.
FIGURE A:
3 x 3 = 9
= 9^2
FIGURE B:
11 x 11 = 121
= 121 meters^2
So 121 + 9 = 130
= 130 meters^2
REMEMBER!!!!
THE FORMULA FOR AREA IS LENGTH * WIDTH = AREA
assuming a data set with 20 training outcomes of which 12 are positive, what is the entropy? round your answer to the nearest thousandths place.
Answers
The entropy of the data set can be calculated using the formula: -p(log2p) - (1-p)(log2(1-p)), where p is the proportion of positive outcomes.
Plugging in the values, we get: -12/20(log2(12/20)) - (1-12/20)(log2(1-12/20)) = -0.971. Rounded to the nearest thousandths place, the entropy is -0.971.
The entropy of a dataset is a measure of its impurity or randomness. In your case, you have a dataset with 20 training outcomes, with 12 positive and 8 negative (since 20-12=8). To calculate the entropy, we use the formula:
Entropy = -p(positive) * log2(p(positive)) - p(negative) * log2(p(negative))
First, find the probabilities of positive and negative outcomes:
p(positive) = 12/20 = 0.6
p(negative) = 8/20 = 0.4
Next, plug these probabilities into the entropy formula:
Entropy = -0.6 * log2(0.6) - 0.4 * log2(0.4)
Entropy ≈ 0.971
Thus, the entropy of your dataset, rounded to the nearest thousandth, is 0.971.
To know more about entropy visit:
https://brainly.com/question/20166134
#SPJ11
For annually compounded interest, what rate would result in a single investment doubling in 3 years?
Answers
Work Shown:
\(A = P*(1+r/n)^{n*t}\\\\2P = P*(1+r/1)^{1*3}\\\\2 = (1+r)^{3}\\\\(1+r)^{3} = 2\\\\1+r = \sqrt[3]{2}\\\\r = -1+\sqrt[3]{2}\\\\r \approx 0.25992\\\\\)
That converts to 25.992% after moving the decimal point two spots to the right. Round this value however your teacher instructs.
Find the number of real solutions of each equation using the
discriminant.

Answers
The solutions for each one are:
1) Two real
2) Two complex
3) One real.
How to find the number of real solutions?For a quadratic of the form:
ax² + bx + c = 0
The discriminant is:
D = b² - 4ac
if D > 0, there are two real solutions.
if D= 0 there is one real solution.
if D < 0 the solutions are complex.
The first quadratic equation is:
2x² + 4x + 3 = 0
The discriminant is:
D = 4² - 4*2*3
= 16 - 24 = -8
So this equation has no real solutions.
The second is:
3x² - 5x + 1 = 0
The discriminant is:
D = (-5)² - 4*3*1
= 25 - 12 = 13
Two real solutions.
The last one is:
x² + 4x + 4 =0
We have:
D = 4² - 4*4*1
= 16 - 16 =0
One real solution.
Learn more about quadratic equations at:
https://brainly.com/question/1214333
#SPJ1
This is adding linear equations:
1. (–6x + 3) + (5x – 4)
2. (–2x + 10) + (–8x – 1)
3. (–4x + 6) + (x – 5)
4. (1.3x + 2.4) + ( –6.1x – 3.2)
5. (0.5x – 0.6) + (0.75x – 0.1)
6. (–7x – 14) + (x – 6)
7. (9x + 7) + (x + 3)
8. (4x – 1) + (–5x + 17)
I honestly just need help, so you can just do one of any problem on here, then I'd just need it to be explained and answered so that I understand
Answers
2. -10x+9
3. -3x+1
4. -4.8x-0.8
5. -1.25x-0.7
6. -6x-20
7. 10x+10
8. -x+16
You’re welcome
Can you solve for X inside the correct code for question four?

Answers
Answer
CIAD
Step-by-step explanation
The Pythagorean theorem states:
\(c^2=a^2+b^2\)where a and b are the legs and c is the hypotenuse of a right triangle.
Applying this theorem to triangle 1:
\(\begin{gathered} x^2=77^2+36^2 \\ x^2=5929+1296 \\ x^2=7225 \\ x=\sqrt{7225} \\ x=85 \end{gathered}\)Then, the first letter is C.
Applying the theorem to triangle 2:
\(\begin{gathered} x^2=39^2+80^2 \\ x^2=1521+6400 \\ x^2=7921 \\ x=\sqrt{7921} \\ x=89 \end{gathered}\)Then, the second letter is I.
Applying the theorem to triangle 3:
\(\begin{gathered} x^2=25^2+100^2 \\ x^2=625+10000 \\ x^2=10625 \\ x=\sqrt{10625} \\ x=103.08 \end{gathered}\)Then, the third letter is A.
Applying the theorem to triangle 4:
\(\begin{gathered} x^2=17^2+52^2 \\ x^2=289+2704 \\ x^2=2993 \\ x=\sqrt{2993} \\ x=54.71 \end{gathered}\)Then, the fourth letter is D.
6. A bought 3 3 by 2 kg of wheat and 2 1 by 2kg of rice. Find the total weight of wheat and rice
bought.......
please answer the question proccesfuly.
the answer which is the best I will mark it as braunlist.
Answers
Answer:
Step-by-step explanation:544
Answer:
total weight of wheat and rice is 8 kg
Step-by-step explanation:
rice = \(3\frac{3}{2}\)
=3*2+3/2
=9/2
wheat = \(2\frac{1}{2}\)
=2*2+1/2
=5/2
total weight of wheat and rice = \(\frac{7}{2} + \frac{9}{2}\)
since their denominator are same u can add numerators.
=7 +9/2
=16/2
=8
Trapezoid W′X′Y′Z′ is the image of trapezoid WXYZ under a dilation through point C. What scale factor was used in the dilation? −7/3 −3/7 3/7 7/3
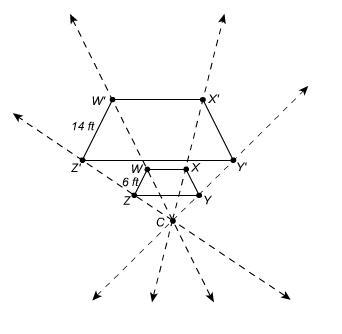
Answers
14 / 6 = 7/3.
Therefore, 7/3 is the scale factor used in this dilation.
The scale factor is the ratio of the new measurement to the old measurement. The scale factor that was used in the dilation is 7/3.
How to calculate the scale factor?Suppose the initial measurement of a figure was x units.
And let the figure is scaled and the new measurement is of y units.
Since the scaling is done by multiplication of some constant, that constant is called the scale factor. Let that constant be 's'.
Then we have:
\(s \times x = y\\s = \dfrac{y}{x}\)
Thus, the scale factor is the ratio of the new measurement to the old measurement.
Scale factor
= Dimension of the new shape ÷ Dimension of the original shape
= 14ft / 6ft
= 7ft / 3ft
Hence, the scale factor that was used in the dilation is 7/3.
Learn more about Scale Factor here:
https://brainly.com/question/22312172
#SPJ5
lucinda surveyed 50 students in her school to find out how many students enjoy playing sports. the resultsare shown in the table. do you think lucinda chose a random sample? why or why not?
Answers
If Lucinda used a random selection method, made an effort to ensure that the sample is representative, and the sample size is large enough, then it's possible that the sample is indeed random.
what are perpendicular lines?
Perpendicular lines are two lines that intersect at a 90-degree angle, forming four right angles at the point of intersection. In other words, if you were to draw a perpendicular line from one of the lines to the other at their point of intersection, it would form a right angle with each of the original lines.
Without having access to more information about how Lucinda selected the sample of students, it's difficult to determine whether or not the sample is truly random.
However, there are a few things that we can consider when trying to determine whether or not the sample is random. For example:
Did Lucinda use a random selection method to choose the students? If she simply surveyed her friends or classmates, for example, the sample would not be random.
Did Lucinda make any effort to ensure that the sample is representative of the larger population of students? For example, did she make sure to include students from a variety of grades, genders, and ethnic backgrounds.
Therefore, if Lucinda used a random selection method, and made an effort to ensure that the sample is representative, and the sample size is large enough, then it's possible that the sample is indeed random.
To learn more about perpendicular lines here is the given link -
https://brainly.com/question/18271653
#SPJ1
II. Given F = (3x² + y)i + (x - y); along the following paths. A. Is this a conservative vector field? If so what is the potential function, f? B. Find the work done by F a) in moving a particle alon
Answers
We are given a vector field F and we need to determine if it is conservative vector. If it is, we need to find the potential function f. Additionally, we need to find the work done by F along certain paths.
To determine if the vector field F is conservative, we need to check if its curl is zero. Computing the curl of F, we find that it is zero, indicating that F is indeed a conservative vector field. To find the potential function f, we can integrate the components of F with respect to their respective variables. Integrating (3x² + y) with respect to x gives us x³ + xy + g(y), where g(y) is the constant of integration. Similarly, integrating (x - y) with respect to y gives us xy - y² + h(x), where h(x) is the constant of integration. The potential function f is the sum of these integrals, f(x, y) = x³ + xy + g(y) + xy - y² + h(x). To find the work done by F along a path, we need to evaluate the line integral ∫ F · dr, where dr represents the differential displacement along the path. We would need more information about the specific paths mentioned in order to calculate the work done.
To know more about conservative vector here: brainly.com/question/32064186
#SPJ11
If there are 20 girls and 30 boys what is the percentage of boys
Answers
Answer:
60%
Step-by-step explanation:
convert to hundreds:
30 out of 50 is the same as 60 out of 100, aka 60%.
Answer:
60 percent
Step-by-step explanation:
50 total
50 is 10 percent
30/50 r boys
60/100 = 60 percent boys
How can we find that when a system of two equations, two unknowns has Infinite Solutions. I want a solution with matrix. I know this method (which is not with matrix):
Answers
Step-by-step explanation:
To determine if a system of two equations with two unknowns has infinite solutions using matrices, you can perform Gaussian elimination or row reduction on the augmented matrix of the system. If the reduced form of the matrix is the identity matrix, then the system has a unique solution. If the reduced form is a row of zeros except for the last column, then the system has no solution. If the reduced form has a row with all zeros except for the last column being non-zero, then the system has an infinite number of solutions.
In other words, the system has infinite solutions if the row reduced form of the augmented matrix has a row of the form [0 0 c], where c is a non-zero scalar. This means that there is a non-trivial solution that satisfies the equation, indicating that there are infinitely many solutions.
A 2-column table with 5 rows. Column 1 is labeled Number of chores, x with entries 2, 4, 6, 8, 10. Column 2 is labeled Days, y with entries 1, 2, 3, 4, 5. The table shows the number of days required to perform a given number of chores. The number of days varies directly with the number of chores. What is the constant of variation? 2 3 One-half One-third\
Answers
The constant of variation based on the information is one half.
How to illustrate the information?From the information given, when x is 2, y is 1, when x is 4, y is 2, etc. It should be noted that this is a direct variation.
This will be illustrated as:
y = kx
when y = 1, x = 2.
1 = 2k
Divide both side by 2.
k = 1/2
Therefore, the constant of variation is 1/2.
Learn more about constant of variation on:
brainly.com/question/25215474
#SPJ1
what is the result of 2.130 x 10³ - 6.6 x 10² =
Answers
Answer:
The answer you're looking for is 1470.
Step-by-step explanation:
The method I used was PEMDAS
Since there was no parenthesis, I simplified the exponents.
2.130 x 10³ - 6.6 x 10² = ?
2.130 x 1000 - 6.6 x 100 = ?
After that, I multiplied all terms next to each other.
2.130 x 1000 - 6.6 x 100 = ?
2130 - 660 = ?
The final step I did was to subtract the two final terms and ended up with 1470 as my final answer.
1470 = ?
I hope this was helpful!
find the value of X in the triangle shown in the image

Answers
Answer:
C \(\displaystyle x = 15\)
Step-by-step explanation:
Use the Pythagorean Theorem to define the hypotenuse:
\(\displaystyle a^2 + b^2 = c^2 \\ \\ 12^2 + 9^2 = x^2 \hookrightarrow 144 + 81 = x^2 \hookrightarrow \sqrt{225} = \sqrt{x^2} \\ \\ \boxed{15 = x}\)
I am joyous to assist you at any time.
\( \huge \underline\text{ Hello There}\)
\( \text{We know, Pythagoras Theorem}\)
\(\implies \text{ (Hypotenuse)²= (Base)² + (Altitude)²}\)
\( \text{Here, \red{Hypotenuse}= x, \red{Base}= 9, \red{Altitude}= 12}\)
\( \underline \text{To Find, } \text{Value of'x'}\)
\( \huge \underline\text \red {Solution}\)
\((x) {}^{2} = (9) {}^{2} + ({12})^{2} \\ \implies (x) { }^{2} = 81 + 144 \\ \implies (x) {}^{2} = 225 \\ \implies x = \sqrt{225} \\ \implies x = 15\)
\( \tt{So \: The \: Value \: of'x'= 15}\)
\( \bold{\therefore Hypotenuse= 15}\)
\( \text{Correct Opt. C= x =15}\)
Hope this helpsFind the equation of the line
that passes through the points
(4, 7) and (-2, 6)
Answers
y
=
1
6
x
+
19
3
←
equation in slope-intercept form
Step-by-step explanation:
Answer:
y = -x/6 + 19/3
Step-by-step explanation:
\((y - 7)( - 2 - 4) = (x - 4)(6 - 7) \\ - 6y + 42 = 4 - x \\ x - 6y = - 38 \\ or \\ y = (38 - x) \div 6\)
Solve negative one sixth times the quantity 3 minus 15 times the quantity one third squared end quantity end quantity.
two thirds
18 over 54
negative two ninths
negative two and 42 over 54
Answers
Negative one sixth times the quantity 3 minus 15 times the quantity one third squared end quantity end quantity will be C. negative two ninths
How to compute the expression?Based on the information given, the expression will be:
= 1/6 ×( 3 - 15 ) × (1/3)²
= -1/6 × -12 × 1/9
= -2 × 1/9
= -2/9
In conclusion, the correct option is D.
Learn more about expressions on:
brainly.com/question/723406
#SPJ1
David rented a truck for one day. there was a base fee of $14.99 and there was an additional charge of 94 cents for each mile driven. david had to pay $209.57 when he returned the truck. for how many miles did he drive the truck
Answers
To determine the number of miles David drove the truck, we need to subtract the base fee and divide the remaining amount by the additional charge per mile.
Let's denote the number of miles driven by 'm'. The equation can be set up as follows:
$209.57 - $14.99 = $0.94 * m
Simplifying the equation:
$194.58 = $0.94 * m
To solve for 'm', we divide both sides of the equation by $0.94:
m = $194.58 / $0.94
m ≈ 206.7
Therefore, David drove the truck for approximately 206.7 miles. Since it's not possible to drive a fraction of a mile, we can assume that David drove either 206 or 207 miles, depending on the rounding convention used.
To learn more about equation : brainly.com/question/29657983
#SPJ11
The diagonal of a square is 15 inches. Find the area of the square.
Answers
Answer:
112.5in²
Step-by-step explanation:
Answer
\(225in^{2}\)
Step-by-step explanation:
hope this helped :-)
Work out the size or angle X

Answers
Answer:
180-132
Step-by-step explanation:
the entire angle should sum to 180
Answer:
48 °
Step-by-step explanation:
132° + x° = 180° (Linear pair)
∴ x° = 180° - 132°
∴ x° = 48°
Hope this helps :) !!!
An item costs $320 before tax, and the sales tax is $16.
Find the sales tax rate. Write your answer as a percentage.
Answers
Brainly needs 20 characters
On Tuesday, Jessica paid $14.12 each on two tickets to a movie theater. Popcorn was
$3.98, but Jessica didn't buy any. She also borrowed a movie for $5.93. Jessica paid
with two $20 bills. How much change did Jessica get?
Answers
Answer:
14.12 × 2 + 5.93 = 34.17
40$ - 34.17 = 5.83$
Answer:
$14.12+$14.12=$28.24+$5.93=$34.17
Change is $6.83
7x2+6x+9
-(4x2+2x+1)
Answers
Answer:
\(3x^2+4x+8\)
Step-by-step explanation:
To find the value of \(7x^2+6x+9-4x^2-2x-1\)
We need to combine like terms by grouping
\(7x^2-4x^2+6x-2x+9-1\)
= \(3x^2+4x+8\)
Hope this helps :)
Have a great day!
whats 2 ( 4 + 7 ) =
Answers
Answer:
22. first multiply two with the digits and signs then add
So using order of operations (parentheses, exponents, multiplication & division, addition & subtraction), you have to do 4+7 inside the parentheses first, then multiply that by 2.
4+7=11
11×2=22
2(4+7)=22
♡ Hope this helps! ♡
❀ 0ranges ❀
set up proportion and solve:
3 packages of blueberries cost $9. How many packages can you buy for $18?
Answers
Answer:
3/9=3
3*18=54
you can buy 54 packages
Step-by-step explanation:
Answer:
6
Step-by-step explanation:
3/9=x/18
3/9=1/3
so 1/3=x/18
cross product
3*x=1*18
3x=18
x=18/3
x=6
Plz help me with this

Answers
Answer:
BALLZ
Step-by-step explanation:
T3ST1CALZ
Given: ∆MNP, PM = 8 m∠P = 90°, m∠N = 58° Find: Perimeter of ∆MNP
(Not 22.4 or 22.43)
Please answer ASAP, brainly awarded.
Answers
Answer:
Step-by-step explanation:
Triangle MNP is a right triangle with the following values:
m∠P = 90°m∠N = 58°PM = 8Interior angles of a triangle sum to 180°. Therefore:
m∠M + m∠N + m∠P = 180°
m∠M + 58° + 90° = 180°
m∠M + 148° = 180°
m∠M = 32°
To find the measures of sides MN and NP, use the Law of Sines:
\(\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}\)
Substitute the values into the formula:
\(\dfrac{MN}{\sin P}=\dfrac{NP}{\sin M}=\dfrac{PM}{\sin N}\)
\(\dfrac{MN}{\sin 90^{\circ}}=\dfrac{NP}{\sin 32^{\circ}}=\dfrac{8}{\sin 58^{\circ}}\)
Therefore:
\(MN=\dfrac{8\sin 90^{\circ}}{\sin 58^{\circ}}=9.43342722...\)
\(NP=\dfrac{8\sin 32^{\circ}}{\sin 58^{\circ}}=4.99895481...\)
To find the perimeter of triangle MNP, sum the lengths of the sides.
\(\begin{aligned}\textsf{Perimeter}&=MN+NP+PM\\&=9.43342722...+4.99895481...+8\\&=22.4323820...\\&=22.43\; \sf units\; (2\;d.p.)\end{aligned}\)

Find the union and intersection of each of the following families or indexed collections. For each natural number n, let Bn = N - {1,2, 3,...,n } and let = {Bn:n N}. For each n N, let Mn = {..., -3n, -Zn, -n, 0, n, 2n, 3n,...}, and let M = {Mn: n N}.
Answers
Let's first find the union and intersection for B.
1. For the collection B:
Recall that Bn = N - {1, 2, 3, ..., n} and B = {Bn: n ∈ N}.
a) Union of B:
To find the union of B, we need to consider all elements in any Bn. Since Bn excludes the first n natural numbers, the union will include all natural numbers greater than n for all n. In other words, the union will contain all natural numbers.
Union(B) = N
b) Intersection of B:
To find the intersection of B, we need to consider elements common to all Bn. Observe that, as n increases, Bn excludes more natural numbers. Therefore, there will be no natural numbers common to all Bn.
Intersection(B) = ∅
2. For the collection M:
Recall that Mn = {..., -3n, -2n, -n, 0, n, 2n, 3n, ...} and M = {Mn: n ∈ N}.
a) Union of M:
To find the union of M, we need to consider all elements in any Mn. Since every Mn contains multiples of n, the union will contain all multiples of natural numbers.
Union(M) = {k * n: k ∈ Z, n ∈ N}
b) Intersection of M:
To find the intersection of M, we need to consider elements common to all Mn. Observe that the only element common to all Mn is 0, as it is a multiple of every natural number.
Intersection(M) = {0}
So, for the indexed collections B and M, we found:
- Union(B) = N
- Intersection(B) = ∅
- Union(M) = {k * n: k ∈ Z, n ∈ N}
- Intersection(M) = {0}
To know more about unions and intersections refer here:
https://brainly.com/question/28337869?#
#SPJ11