Question If f(x)=2x−3 and g(x)=4x+5, what is (f⋅g)(x)?
Answers
Answer:
f * g)(x) = 8x^2 - 2x - 15
Step-by-step explanation:
Since we want to find (f * g)(x), we want to multiply the entire functions and leave the answer in terms of x (in terms of x simply means we do the multiplication and the simplified answer will be in terms of x):
Thus, we have (2x - 3)(4x + 5). This is a binomial expression and we can multiply binomials using the FOIL method, where
"F" refers to the first terms (2x and 4x in this case),"O" refers to the outer terms (2x and 5),"I" refers to the inner terms (-3 and 4x),and "L" refers to the last terms (-3 and 5)We add all the terms and combine like terms to find (f * g)(x):
(2x * 4x) + (2x * 5) + (-3 * 4x) + (-3 * 5)
8x^2 + 10x - 12x - 15
8x^2 - 2x - 15
Thus, (f * g)(x) is 8x^2 - 2x - 15
Related Questions
Find the least common multiple (LCM) of 7, 10, and 20.
200
140
20
70
Answers
Answer:
140
Step-by-step explanation:
140 is the first multiple that all 3 numbers share.
When finding the multiples of 7,10, and 20, the first number you see they all have in common besides 1, is 140
16 families went on a trip which cost them Rs 2,16,352. How much did each
family pay?
Answers
Given that 16 families went on a trip and the cost of the trip was Rs. 2,16,352.The amount paid by each family is to be determined by unitary method Hence each family paid Rs.13522
Now, let's solve this by using the method of unitary method. To find the cost of 1 family trip, we will divide the total cost of the trip by the number of families.2,16,352 / 16 = 13,522 So, the cost of the trip per family is Rs. 13,522.Hence, each family paid Rs. 13,522 for the trip.
to know more about unitary method
https://brainly.com/question/28276953
Answer:
Step-by-step explanation
1. The total cost of the trip for all 16 families is Rs 2,16,352.
2. To find out how much each family paid, we need to divide the total cost by the number of families: Rs 2,16,352 ÷ 16.
3. When we do the division, we get the result: Rs 13,522.
Now let's check if this result is correct:
1. If each family paid Rs 13,522 for the trip, then the total cost for all 16 families would be: 16 × Rs 13,522 = Rs 2,16,352.
2. This is exactly the same as the total cost given in the problem statement.
So we have shown that each family paid **Rs 13,522** for the trip
Which equation represents a nonlinear
Function
2y = 1/2x + 5
y = 1/2x - 5
3y = 1/2x + 5
4y = (1/2)^x -5
Answers
Answer:
4y = (1/2)^x -5
Step-by-step explanation:
The first three equations are lines. All the variables have a power of just one (power of one is a math number that is not written) They are actually all written in slope-intercept form even. Line equations are linear function. Yay the words match!
You get a curve (not linear) when you have exponents, square roots or variables in the denominator of a fraction. Or as here, a variable for an exponent!
$8,000 is invested in an account earning 8.7% interest (APR), compounded continuously. Write a function showing the value of the account after tt years, where the annual growth rate can be found from a constant in the function. Round all coefficients in the function to four decimal places. Also, determine the percentage of growth per year (APY), to the nearest hundredth of a percent.
Answers
i believe it would be 8k divided by 8.7 pie
Diven {x) = 3x- 1 and 9(x) = 2x-3, for which value of x does g(X) = {2)?
Answers
The calculated value of x at g(x) = 2 is x = 2.5
How to determine the value of x at g(x) = 2from the question, we have the following parameters that can be used in our computation:
f(x) = 3x - 1
Also, we have
g(x) = 2x - 3
When g(x) - 2, we have
2x - 3 = 2
So, we have
2x = 5
Divide by 2
x = 2.5
Hence, the value of x at g(x) = 2 is x = 2.5
Read more about function at
https://brainly.com/question/27915724
#SPJ1
Write an equation of the line that is parallel to y = 1/2x + 3 and passes through the point (2,-4). A) y = 1/2x-4 - 15 B) y = -2x-4 + 15 C) y = -2x-5 D) y = 1/2x - 5
Answers
Answer:
D
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
y = \(\frac{1}{2}\) x + 3 ← is in slope- intercept form
with slope m = \(\frac{1}{2}\)
• Parallel lines have equal slopes , then
y = \(\frac{1}{2}\) x + c ← is the partial equation
to find c substitute (2, - 4 ) into the partial equation
- 4 = \(\frac{1}{2}\) (2) + c = 1 + c ( subtract 1 from both sides )
- 5 = c
y = \(\frac{1}{2}\) x - 5 ← equation of parallel line
Convert the number to standard notation.
6.0253 × 109
Answers
Answer:656.7577
Step-by-step explanation:
What is are the answers

Answers
Answer:
Q1(a). x=112 (corr angles)
Q1(b). x=75 (alt angles)
Q1(c). x=180-150 (adj angles on a str line)
=30
y=150 (corr angles)
Q1(d). x=99 (vert opp angles)
y=99 (corr angles)
z=180-99 (adj angles on a str line)
=81
Q1(e). x=180-74 (adj angles on a str line)
=106
y=106 (corr angles)
Q1(f). x=123 (corr angles)
y=180-110 (int angles)
=70
Q3. 4x+15=5x-10 (vert opp angles)
4x-5x=-10-15
-x=-25
x=25
Q4. x+22+2x-13=180 (int angles)
3x+9=180
3x=180-9
=171
x=171÷3
=57
95% of what number is 114?
Answers
114 is 95% of 120
100% of 120 is 120, therefore 95 percent of 120 equals 114. To learn how to solve 114 is 95 percent of what number, see the step-by-step instructions below.
114 is 95 Percent of What Number?
Formula = Number x 100
Percent = 114 x 100
95 = 120
The following shows the steps to derive this formula and find out 95% of the number is 114.
Step 1: If 95% of a number is 114, then what is 100% of that number? Set up the equation.
114
95% = Y
100%
Step 2: Solve for Y
Using cross multiplication of two fractions, we get
95Y = 114 x 100
95Y = 11400
Y = 11400
100 = 120
solve for x in the equation x2+6x-6=10
Answers
Answer:
Step-by-step explanation:
\(x^{2} + 6x-6= 10\\x^{2} +6x-16=0\\x^{2} -2x+8x-16=0\\x(x-2)+8(x-2)=0\\(x-2)(x+8)=0\\x = 2\\or\\x = -8\)
Answer:
X = 2 and X = -8
Step-by-step explanation:
X2 + 6X - 6-10 = 0 ....... when +10 pass the equality sign it will become -10
X2 + 6X -16 =0
here we need to find if there are two numbers there sum is +6 and there product is -16.
here we need to find if there are two numbers there sum is +6 and there product is -16.The two numbers are -2 and +8
-2+8= +6
-2*8= -16
( X - 2 ) * ( X + 8 ) =0
X - 2 = 0 ...... when -2 pass equality sign it will become+2
X = 2
X + 8 =0 ..... when +8 pass equality sign it will become -8
X = -8
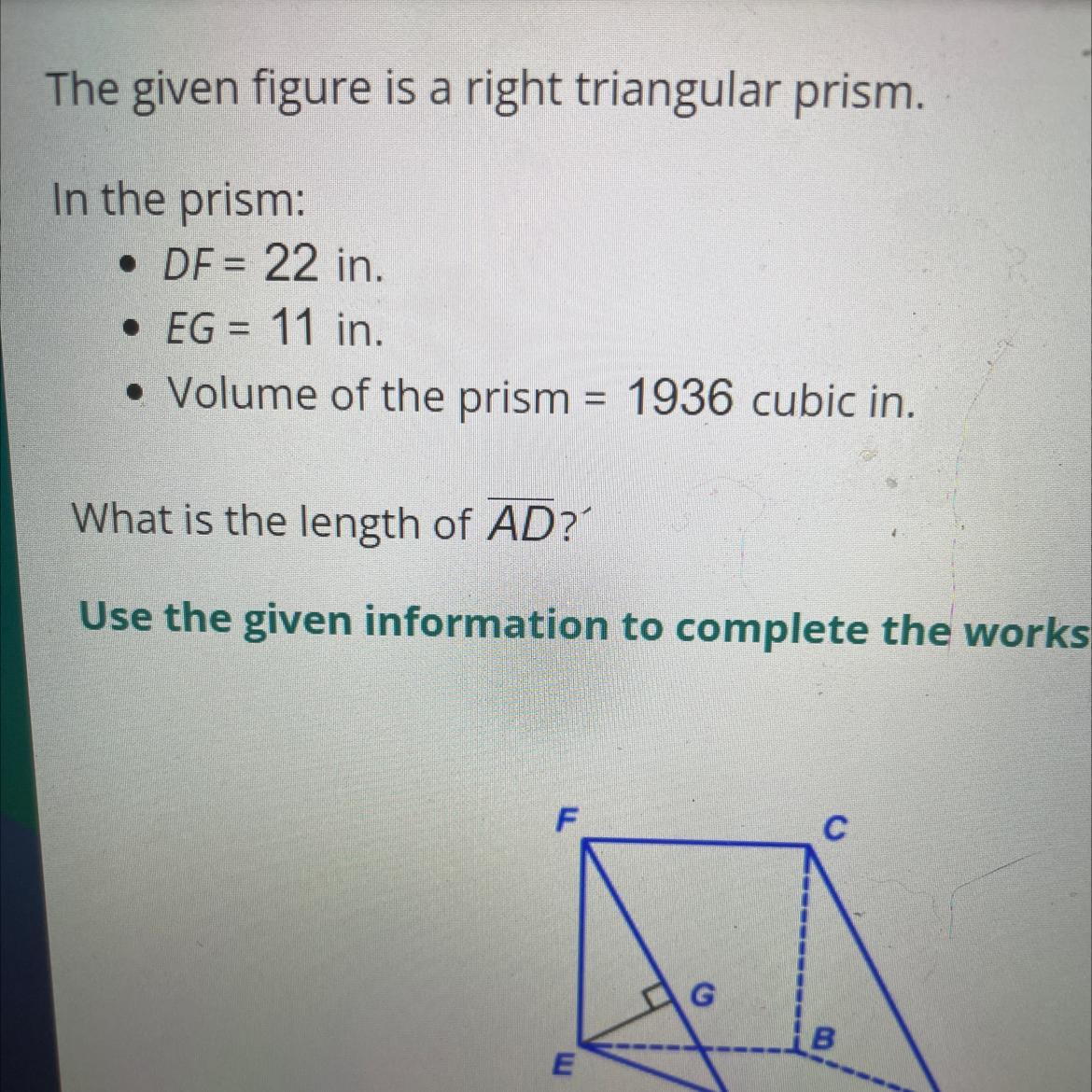
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
What is the length of AD?'
Use the given information to complete the worksheet.
Thank you!
Answers
The length of side AD is,
⇒ AD = 16
We have to given that;
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
Since, Volume of right triangular prism is,
V = 1/2 (bh) x L
Substitute all the values we get;
V = 1/2 (22 × 11) × AD
1936 = 121 × AD
AD = 16
Thus, The length of side AD is, 16
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
How can I resolve (with steps) 2*(4^2x+3) = 1/8
Answers
Answer:
-47/256
Step-by-step explanation:
Divided both sides by 2
2(4^2+3)/2=1/8/2
Simplify
16x+3=1/16
Subtract 3 from both sides
16x+3-3=1/16-3
Simplify
16x=-47/16
Divided both sides by 16
16x/16=-47/16/16
Simplify
x=-47/256
Hope this helped! :)
Answer:
rephrase the question plz
Step-by-step explanation:
Select three ratios that are equivalent to 11:1.
Choose 3 answers:
A(1:11
B(22:2
C(55:5
D(9:99
E(110:10
Answers
Answer:
B,C and D is the answer of this question
find two square roots of 49
Answers
Answer:
its 7.
Step-by-step explanation:
7 x 7 = 49
simple
find the missing angles in each triangle
PLS HELP I WILL GIVE U BRANLIEST I NEED ANSWERS AHHHH

Answers
Answer:
50°
Step-by-step explanation:
Please see the attached picture for the full solution.

Solve the system of 3×3 linear equations using elementary row operations

Answers
We want to solve the following system
\(\begin{cases}4x+3y-8z=-19 \\ x+y-2z=-4 \\ 3x+2y-5z=-13\end{cases}\)using the elimination method.
Gaussian elimination is the name of the method we use to perform the three types of matrix row operations on an augmented matrix coming from a linear system of equations in order to find the solutions for such system.
The Gaussian elimination rules are the same as the rules for the three elementary row operations, in other words, you can algebraically operate on the rows of a matrix in the next three ways (or combination of):
1 - Interchanging two rows
2 - Multiplying a row by a constant (any constant which is not zero)
3 - Adding a row to another row
We start our process by converting the system into an augmented matrix.
\(\begin{cases}4x+3y-8z=-19 \\ x+y-2z=-4 \\ 3x+2y-5z=-13\end{cases}\Leftrightarrow\begin{bmatrix}4 & 3 & -8 & \bigm| & -19 \\ 1 & 1 & -2 & \bigm| & -4 \\ 3 & 2 & -5 & \bigm| & -13\end{bmatrix}\)Now, starting the elimination process, we can add (-4) times the second row to the first row and add (-3) times the second row to the third row.
\(\begin{bmatrix}4 & 3 & -8 & \bigm{|} & -19 \\ 1 & 1 & -2 & \bigm{|} & -4 \\ 3 & 2 & -5 & \bigm{|} & -13\end{bmatrix}\rightarrow\begin{bmatrix}0 & -1 & 0 & \bigm{|} & -3 \\ 1 & 1 & -2 & \bigm{|} & -4 \\ 0 & -1 & 1 & \bigm{|} & -1\end{bmatrix}\)Then, interchanging the first and the second row
\(\begin{bmatrix}0 & -1 & 0 & \bigm{|} & -3 \\ 1 & 1 & -2 & \bigm{|} & -4 \\ 0 & -1 & 1 & \bigm{|} & -1\end{bmatrix}\rightarrow\begin{bmatrix}1 & 1 & -2 & \bigm{|} & -4 \\ 0 & -1 & 0 & \bigm{|} & -3 \\ 0 & -1 & 1 & \bigm{|} & -1\end{bmatrix}\)Adding the second row to the first row, we have
\(\begin{bmatrix}1 & 1 & -2 & \bigm{|} & -4 \\ 0 & -1 & 0 & \bigm{|} & -3 \\ 0 & -1 & 1 & \bigm{|} & -1\end{bmatrix}\rightarrow\begin{bmatrix}1 & 0 & -2 & \bigm{|} & -7 \\ 0 & -1 & 0 & \bigm{|} & -3 \\ 0 & -1 & 1 & \bigm{|} & -1\end{bmatrix}\)Multiplying the second row by (-1), we have
\(\begin{bmatrix}1 & 0 & -2 & \bigm{|} & -7 \\ 0 & -1 & 0 & \bigm{|} & -3 \\ 0 & -1 & 1 & \bigm{|} & -1\end{bmatrix}\rightarrow\begin{bmatrix}1 & 0 & -2 & \bigm{|} & -7 \\ 0 & 1 & 0 & \bigm{|} & 3 \\ 0 & -1 & 1 & \bigm{|} & -1\end{bmatrix}\)Adding the second row to the third row
\(\begin{bmatrix}1 & 0 & -2 & \bigm{|} & -7 \\ 0 & 1 & 0 & \bigm{|} & 3 \\ 0 & -1 & 1 & \bigm{|} & -1\end{bmatrix}\rightarrow\begin{bmatrix}1 & 0 & -2 & \bigm{|} & -7 \\ 0 & 1 & 0 & \bigm{|} & 3 \\ 0 & 0 & 1 & \bigm{|} & 2\end{bmatrix}\)And finally, adding 2 times the third row to the first, we have
\(\begin{bmatrix}1 & 0 & -2 & \bigm{|} & -7 \\ 0 & 1 & 0 & \bigm{|} & 3 \\ 0 & 0 & 1 & \bigm{|} & 2\end{bmatrix}\rightarrow\begin{bmatrix}1 & 0 & 0 & \bigm{|} & -3 \\ 0 & 1 & 0 & \bigm{|} & 3 \\ 0 & 0 & 1 & \bigm{|} & 2\end{bmatrix}\)Converting this matrix back to a system, we have
\(\begin{bmatrix}1 & 0 & 0 & \bigm{|} & -3 \\ 0 & 1 & 0 & \bigm{|} & 3 \\ 0 & 0 & 1 & \bigm{|} & 2\end{bmatrix}\rightarrow\begin{cases}x=-3 \\ y=3 \\ z=2\end{cases}\)Therefore, our solution is
\((x,y,z)=(-3,3,2)\)What is the number of significant figures in 122.35 cm ?
Answers
Answer:
5
Step-by-step explanation:
HELP I will mark brainliest
20) Are the two angles similar? Explain your reasoning.
(It’s number 20)

Answers
Find the value of x in the triangle shown below. x = 56° 99°

Answers
Answer:
x = 25 degrees
Step-by-step explanation:
All angles in a triangle should add up to 180 degrees. So to solve for x, set up an equation where all three angles added up equals 180.
180 = 99 + 56 + x
180 = 155 + x
25 = x
The unknown angle is equal to 25 degrees.
Loan application
A loan officer at a bank receives an application for a loan from a new customer. The customer claims to have a credit score above 700, but the officer is not sure whether to believe them. The officer knows that in the general population, about 20% of people have a credit score above 700. The officer has access to a credit bureau that can verify the customer's credit score with 95% accuracy, i.e., if a person has a credit score above 700, the credit bureau can give a correct report 95% of time, if a person has a credit score below 700, the credit bureau can give a correct report 95% of the time as well.
7. What is the probability that the customer actually has a credit score above 700, given that the credit bureau reports a score above 700? (round to three decimal places)
8. Show your work for the answer above.
Answers
The probability that the customer actually has a credit score above 700, given that the credit bureau reports a score above 700, is approximately 0.995. Bayes' theorem and the law of total probability were used to calculate the probability.
7. The probability that the customer actually has a credit score above 700, given that the credit bureau reports a score above 700, can be calculated using Bayes' theorem:
P(score > 700 | bureau reports score > 700) = P(bureau reports score > 700 | score > 700) * P(score > 700) / P(bureau reports score > 700)
We know that P(score > 700) = 0.20 and P(bureau reports score > 700 | score > 700) = 0.95. To find P(bureau reports score > 700), we can use the law of total probability:
P(bureau reports score > 700) = P(bureau reports score > 700 | score > 700) * P(score > 700) + P(bureau reports score > 700 | score <= 700) * P(score <= 700)
P(bureau reports score > 700) = 0.95 * 0.20 + 0.05 * 0.80
P(bureau reports score > 700) = 0.19
Now we can plug in the values:
P(score > 700 | bureau reports score > 700) = 0.95 * 0.20 / 0.19 ≈ 0.995
Therefore, the probability that the customer actually has a credit score above 700, given that the credit bureau reports a score above 700, is approximately 0.995.
8. P(score > 700 | bureau reports score > 700) = P(bureau reports score > 700 | score > 700) * P(score > 700) / P(bureau reports score > 700)
= 0.95 * 0.20 / (0.95 * 0.20 + 0.05 * 0.80)
= 0.995 (rounded to three decimal places)
We used Bayes' theorem to calculate the probability, and the law of total probability to find P(bureau reports score > 700).
Learn more about probability here: brainly.com/question/30034780
#SPJ4
A dairy needs 258 gallons of milk containing 7% butterfat how many gallons each of milk containing 8% butterfat and milk containing 2% butterfat must be used to obtain the desired 258 gallons
Answers
Let's assume x gallons of milk containing 8% butterfat and y gallons of milk containing 2% butterfat are used.
The total amount of milk is x + y gallons, and we want it to be equal to 258 gallons.
To determine the amount of butterfat in the mixture, we can multiply the volume of each type of milk by its respective butterfat percentage and sum them up.
For milk containing 8% butterfat, the amount of butterfat is 0.08x (8% is equivalent to 0.08 as a decimal).
For milk containing 2% butterfat, the amount of butterfat is 0.02y (2% is equivalent to 0.02 as a decimal).
Since we want the final mixture to contain 7% butterfat, we can set up the following equation:
0.08x + 0.02y = 0.07(258)
Simplifying the equation, we have:
0.08x + 0.02y = 18.06
To solve for x and y, we need another equation. Since the total amount of milk is x + y = 258, we can rearrange it to y = 258 - x.
Substituting this value into the equation above, we get:
0.08x + 0.02(258 - x) = 18.06
Solving this equation will give us the values of x and y, which represent the gallons of milk containing 8% butterfat and 2% butterfat, respectively, needed to obtain the desired 258 gallons.
For such more question on gallons
https://brainly.com/question/28274339
#SPJ8
differenciate the Function 1/ X3
Answers
Step-by-step explanation:
To differentiate the function f(x) = 1/x^3, we can use the power rule of differentiation. Here's the step-by-step process:
Write the function: f(x) = 1/x^3.
Apply the power rule: For a function of the form f(x) = x^n, the derivative is given by f'(x) = nx^(n-1).
Differentiate the function: In our case, n = -3, so the derivative is:
f'(x) = -3 * x^(-3-1) = -3 * x^(-4) = -3/x^4.
Therefore, the derivative of the function f(x) = 1/x^3 is f'(x) = -3/x^4.
which holds the more capacity 0.75 litres or 350ml
Answers
Answer:
0.75 liters
Step-by-step explanation:
1000ml in 1 liter so 0.75*1000=750ml
750ml > 350ml
simplify the expresion (5÷5)+5×(5²- 5)
Answers
Answer: 101
Step-by-step explanation: 1+5x20 then 100+1= 101
Susan bought a 1 kilogram bag of grapes. On the way home, she ate 125 grams of the grapes. How many grams of grapes does Susan have left? use math language and symbols to explain how you used the correct measurement units to solve the problem.
Answers
Susan has 875 grams of grapes left.
1. Susan bought a 1 kilogram bag of grapes, which is equivalent to 1000 grams (since there are 1000 grams in a kilogram).
2. Susan ate 125 grams of the grapes on her way home.
3. To find out how many grams of grapes Susan has left, we need to subtract the amount she ate from the initial weight of the bag. Therefore, we subtract 125 grams from 1000 grams.
1000 grams - 125 grams = 875 grams
4. Thus, Susan has 875 grams of grapes left.
measurement units:
In this problem, we used grams as the measurement unit. Grams are commonly used to measure the weight of small objects like grapes. Since the problem stated that Susan bought a 1 kilogram bag of grapes, it was necessary to convert the kilogram measurement to grams.
This conversion was done by multiplying the kilogram value by 1000 (1 kilogram = 1000 grams). By using the correct measurement units, we were able to accurately calculate the amount of grapes Susan had left after eating a portion.
For more such questions on grams, click on:
https://brainly.com/question/29255021
#SPJ8
NEED HELP ASAP!!! will give brian list!

Answers
Answer:
a. 28/143
b. 40/143
Step-by-step explanation:
For both parts, we assume that the teas are selected without replacement. So we start with 13 teas. After one is selected, we have 12 teas left, and then after one more is selected, we have 11 teas left.
a. If all three are sweet:
\( \frac{8}{13} \times \frac{7}{12} \times \frac{6}{11} = \frac{28}{143} \)
b. If exactly one is sweet:
First one sweet, next two unsweet:
\( \frac{8}{13} \times \frac{5}{12} \times \frac{4}{11} = \frac{40}{429} \)
First one unsweet, second one sweet,
third one unsweet:
\( \ \frac{5}{13} \times \frac{8}{12} \times \frac{4}{11} = \frac{40}{429} \)
First two unsweet, third one sweet:
\( \frac{5}{13} \times \frac{4}{12} \times \frac{8}{11} = \frac{40}{429} \)
Adding these probabilities, we have
\( \frac{120}{429} = \frac{40}{143} \)
drag tiles to the boxes to form correct pairs. match the cube roots and square roots with their values.

Answers
the cubed root of 729 is 9
the square root of 100 is 10
the cubed root of 216 is 6
the square root of 64 is 8
and the cubed root of 343 is 7
This should be right
Bandhan Bank employee salary after 10 years
Answers
Answer:
- Banking Operations salary in India with less than 1 year of experience to 10 years ranges from ₹ 1.4 Lakhs to ₹ 7 Lakhs with an average annual salary of ₹ 3.1 Lakhs based on 261 latest salaries
Rylon Corporation manufactures Brute and Chanelle perfumes. The raw materials needed to manufacture each type of perfume can be purchased for $3 per pound. Processing 1 lb of raw material requires 1 hour of laboratory time. Each pound of processed raw material yields 3 oz of Regular Brute Perfume and 4 oz of Chanelle perfume. Regular Brute can be sold for $7/oz and Regular Chanelle for $6/oz. Rylon also has the option of further processing Regular Brute and Regular Chanelle to produce Luxury Brute, sold at $18/oz, and Luxury Chanelle, sold at $14/oz. Each ounce of Regular Brute processed further requires an additional 3 hours of laboratory time and $4 processing cost and yields 1 oz of Luxury Brute. Each ounce of Regular Chanelle processed further requires an additional 2 hours of laboratory time and $4 processing cost and yields 1 oz of Luxury Chanelle. Each year, Rylon has 6,000 hours of laboratory time available and can purchase up to 4,000 lb of raw material. Question : what is the simplex algorithm (manual table ) to find a solution to the linear programming problem given above
Answers
Convert the problem to standard form and write the initial tableau with slack variables:
Maximize
\(Z = 7*3 + 6*4 + 18*5 + 14*6 - 3*1 - 3*2 - 4*5 - 4*6\)
Subject to:
\(x1 + x2 + s1 = 4000\\x3 - (1/3)*1 + (1/3)*5 = 0\\x4 - (1/3)*2 + (1/2)*6 = 0\\x3*1 + 3*2 + 3*3 + 3*4 + 3*5 + 2*6 + s2 = 6000\)
All variables are non-negative.
Tableau
x1 x2 x3 x4 x5 x6 s1 s2 b
Z -3 -3 7 6 18 14 0 0 0
s1 1 1 0 0 0 0 1 0 4000
s2 3 3 3 3 3 2 0 1 6000
x5 0 0 1 0 1/3 0 0 0 0
x6 0 0 0 1 0 1/2 0 0 0
The basic variables are s1, s2, x5, and x6.
Step 1: Choose entering variable. The most positive coefficient in objective row is 18, corresponding to x5. x5 enters the basis.
Step 2: Choose the leaving variable. The minimum ratio of right-hand side to coefficient of x5 is 12000/(1/3) = 36000,
corresponding to s1. s1 leaves the basis.
Step 3: Perform, pivot operation to make x5 the basic variable for s1. Divide, pivot row by 1/3 and subtract appropriate multiples of the pivot row from other rows to make other entries in column 5 zero.
x1 x2 x3 x4 x5 x6 s1 s2 b
Z -3 -3 7 6 18 14 0 0 0
x5 0 0 1 0 1/3 0 0 0 0
s2 3 3 3 3 2 2/3 2/3 0 1/3 24000
x3 1 0 1/3 0 1/3 0 -1/3 0 0
x4 0 1 0 1/3 0 1/2 -1/6 0 0
The basic variables are x5, x3, x4, and s2.
Step 4: Choose the entering variable. The most positive coefficient in the objective row is 7, corresponding to x3. x3 enters the basis.
Step 5: Determine the leaving variable. The right-hand side's minimum ratio to the coefficient of x3 is 0, indicating that x3 can be increased without bound. This implies that the optimal solution is unbounded and that there is no finite optimal value for the problem.
As a result, the simplex algorithm demonstrates that the given linear programming problem lacks a feasible solution. This means that it is not possible to meet all of the constraints at the same time.
For more question on simplex algorithm click on
https://brainly.com/question/29554333
#SPJ4
8. Lisa types 6 pages in 36 minutes. Frank types 5 pages in 30 minutes. Do they type at the same rate? Use a proportion to explain.
Answers
Answer:
Yes
Step-by-step explanation:
Lisa and Frank type at the same rate.
They both type 1 page every six minutes.
Lisa types 6 pages every 36 minutes, and if we divide the minutes by the pages, we get
\(\frac{36}{6} = 6\)
And Frank types 5 pages ever 30 minutes, when we divide we get
\(\frac{30}{5} = 6\)