Lulu's mum pours 210 ml of plant food into a watering con. She adds 150 ml more water than plant food into the watering can to get a mixture. She then pours all of the mixture equally onto 6 plants. How much of the mixture does she pour onto each plant?
Answers
Lulu's mum mixes 360 ml of water with 210 ml of plant food. Each plant will receive 95 ml of mixture.
To find out how much of the mixture Lulu's mum pours onto each plant, we need to first find out the total amount of mixture in the watering can, and then divide that by the number of plants.
Step 1: Find the total amount of mixture in the watering can.
We know that Lulu's mum pours 210 ml of plant food into the watering can. She also adds 150 ml more water than plant food, so she adds 210 ml + 150 ml = 360 ml of water.
The total amount of mixture in the watering can is therefore 210 ml + 360 ml = 570 ml.
Step 2: Divide the total amount of mixture by the number of plants.
We know that there are 6 plants, so we need to divide the total amount of mixture by 6.
570 ml / 6 = 95 ml.
Therefore, Lulu's mum pours 95 ml of the mixture onto each plant.
Learn more about mixture here:
https://brainly.com/question/4337089
#SPJ11
Related Questions
If Y has a binomial distribution with parameters n and p, then p(hat)1 = Y/n is an unbiased estimator of p. Another estimator of p is p(hat)2 = (Y+1)/(n+2).
a. Derive the biase of p(hat)2.
b. Derive MSE(Pphat)1) and MSE(p(hat)2).
c. For what values of p is MSE(p(hat)1) < MSE(p(hat)2)?
Answers
a. To derive the bias of p(hat)2, we need to calculate the expected value (mean) of p(hat)2 and subtract the true value of p.
Bias(p(hat)2) = E(p(hat)2) - p
Now, p(hat)2 = (Y+1)/(n+2), and Y has a binomial distribution with parameters n and p. Therefore, the expected value of Y is E(Y) = np.
E(p(hat)2) = E((Y+1)/(n+2))
= (E(Y) + 1)/(n+2)
= (np + 1)/(n+2)
The bias of p(hat)2 is given by:
Bias(p(hat)2) = (np + 1)/(n+2) - p
b. To derive the mean squared error (MSE) for both p(hat)1 and p(hat)2, we need to calculate the variance and bias components.
For p(hat)1:
Bias(p(hat)1) = E(p(hat)1) - p = E(Y/n) - p = (1/n)E(Y) - p = (1/n)(np) - p = p - p = 0
Variance(p(hat)1) = Var(Y/n) = (1/n^2)Var(Y) = (1/n^2)(np(1-p))
MSE(p(hat)1) = Variance(p(hat)1) + [Bias(p(hat)1)]^2 = (1/n^2)(np(1-p))
For p(hat)2:
Bias(p(hat)2) = (np + 1)/(n+2) - p (as derived in part a)
Variance(p(hat)2) = Var((Y+1)/(n+2)) = Var(Y/(n+2)) = (1/(n+2)^2)Var(Y) = (1/(n+2)^2)(np(1-p))
MSE(p(hat)2) = Variance(p(hat)2) + [Bias(p(hat)2)]^2 = (1/(n+2)^2)(np(1-p)) + [(np + 1)/(n+2) - p]^2
c. To find the values of p where MSE(p(hat)1) < MSE(p(hat)2), we can compare the expressions for the mean squared errors derived in part b.
(1/n^2)(np(1-p)) < (1/(n+2)^2)(np(1-p)) + [(np + 1)/(n+2) - p]^2
Simplifying this inequality requires a specific value for n. Without the value of n, we cannot determine the exact values of p where MSE(p(hat)1) < MSE(p(hat)2). However, we can observe that the inequality will hold true for certain values of p, n, and the difference between n and n+2.
To learn more about binomial distribution: -brainly.com/question/29137961
#SPJ11
In the given scenario, we have two estimators for the parameter p of a binomial distribution: p(hat)1 = Y/n and p(hat)2 = (Y+1)/(n+2). The objective is to analyze the bias and mean squared error (MSE) of these estimators.
The bias of p(hat)2 is derived as (n+1)/(n(n+2)), while the MSE of p(hat)1 is p(1-p)/n, and the MSE of p(hat)2 is (n+1)(n+3)p(1-p)/(n+2)^2. For values of p where MSE(p(hat)1) is less than MSE(p(hat)2), we need to compare the expressions of these MSEs.
(a) To derive the bias of p(hat)2, we compute the expected value of p(hat)2 and subtract the true value of p. Taking the expectation:
E(p(hat)2) = E[(Y+1)/(n+2)]
= (1/(n+2)) * E(Y+1)
= (1/(n+2)) * (E(Y) + 1)
= (1/(n+2)) * (np + 1)
= (np + 1)/(n+2)
Subtracting p, the true value of p, we find the bias:
Bias(p(hat)2) = E(p(hat)2) - p
= (np + 1)/(n+2) - p
= (np + 1 - p(n+2))/(n+2)
= (n+1)/(n(n+2))
(b) To derive the MSE of p(hat)1, we use the definition of MSE:
MSE(p(hat)1) = Var(p(hat)1) + [Bias(p(hat)1)]^2
Given that p(hat)1 = Y/n, its variance is:
Var(p(hat)1) = Var(Y/n)
= (1/n^2) * Var(Y)
= (1/n^2) * np(1-p)
= p(1-p)/n
Substituting the bias derived earlier:
MSE(p(hat)1) = p(1-p)/n + [0]^2
= p(1-p)/n
To derive the MSE of p(hat)2, we follow the same process. The variance of p(hat)2 is:
Var(p(hat)2) = Var((Y+1)/(n+2))
= (1/(n+2)^2) * Var(Y)
= (1/(n+2)^2) * np(1-p)
= (np(1-p))/(n+2)^2
Adding the squared bias:
MSE(p(hat)2) = (np(1-p))/(n+2)^2 + [(n+1)/(n(n+2))]^2
= (n+1)(n+3)p(1-p)/(n+2)^2
(c) To compare the MSEs, we need to determine when MSE(p(hat)1) < MSE(p(hat)2). Comparing the expressions:
p(1-p)/n < (n+1)(n+3)p(1-p)/(n+2)^2
Simplifying:
(n+2)^2 < n(n+1)(n+3)
Expanding:
n^2 + 4n + 4 < n^3 + 4n^2 + 3n^2
To learn more about binomial distribution: -brainly.com/question/29137961
#SPJ11
.........................
I
Answers
Answer:
???
Step-by-step explanation:
Find the solution of the system of equations
15x – 10y = -30
5x – 9y = 7
Answers
Explanation: We can use the elimination method to make two of the variables cancel out.
For the second question, we can multiply everything by -3 to get -15x+27=-21, where 15x and -15x will cancel out.
Adding the remaining equations will give us 17y=-51 and solving for y gives us y=-3.
If we plug -3 in for y in the 2nd original equation, we get 5x+27=-4, where solving for x will give us x=-4
find a monic quadratic polynomial $f(x)$ such that the remainder when $f(x)$ is divided by $x-1$ is $2$ and the remainder when $f(x)$ is divided by $x-3$ is $4$.
Answers
f(x) = x + 1 is the monic quadratic polynomial used here
Given,
The monic quadratic polynomial f(x)
The remainder when f(x) divided by x - 1 is 2
The remainder when f(x) divided by x - 3 is 4
We have to find f(x).
Monic Quadratic Polynomial;-
A monic polynomial in algebra is a univariate polynomial with a single variable and a leading coefficient of 1. Its leading coefficient is the highest degree nonzero coefficient.
Here,
The remainder when f(x) divided by x - 1 is 2
Assume f(x) / x - 1 = 1
Then,
f(x) = (x - 1) × 1 + 2
f(x) = x - 1 + 2
f(x) = x + 1
Next,
The remainder when f(x) divided by x - 3 is 4
Assume f(x) / x - 3 = 1
Then,
f(x) = (x - 3) × 1 + 4
f(x) = x - 3 + 4
f(x) = x + 1
That is,
The monic quadratic polynomial used here is, f(x) = x + 1
Learn more about monic quadratic polynomial here;
https://brainly.com/question/16601143
#SPJ4
Rick builds new homes for Eastover Construction Company. Yesterday, Rick installed a horizontal support beam parallel to the base of a triangular roof. Then, Rick installed a vertical support beam between the top and base of the roof, perpendicular to the horizontal beam and the base of the roof. Along the vertical beam, the distance from the top of the roof to the horizontal beam is 28 feet, and the distance from the horizontal beam to the base of the roof is 42 feet. The base of the roof is 90 feet long.
what is the length of the horizontal beam
Answers
Answer:
90 feet.
Step-by-step explanation:
The horizontal beam is parallel to the base of a triangular roof, and the vertical beam is perpendicular to the horizontal beam and the base of the roof. So the length of the horizontal beam is the same as the base of the roof which is 90 feet.
find the limit (if it exists). lim x→6 f(x) , where f(x)= x2 − 7x 4
if x < 6 −x2, 7x − 8 if x ≥ 6
Answers
The limit does not exist. The left and right limits as x approaches 6 are different, so the overall limit does not exist. The function "jumps" at x = 6.
Consider the left and right limits as x approaches 6:
lim x→6- f(x) = lim x→6- (x² - 7x)/4 = (-6)/4 = -3/2lim x→6+ f(x) = lim x→6+ (-x² + 7x - 8) = -26Since the left and right limits are different, the overall limit does not exist. Intuitively, this is because the function "jumps" at x = 6, taking on very different values on either side of the point. Therefore, the limit as x approaches 6 does not exist.
Learn more about Limit:
https://brainly.com/question/27129946
#SPJ4
1 2/3 yards of chain cost 9.00.
How much money for 1 yard
Answers
Alright nevermind, imma delete this answer.
Answer: $5.40
Step-by-step explanation:
1 and 2/3 yards costs $9
5/3 yards costs $9 <--- changes 1 and 2/3 to improper
5 * 1/3 yards costs $9 <---- 5/3 = 5 * 1/3
1/3 yard costs $9/5 = $1.80 <--- divides the ratio by 5
1 yard costs $1.80 * 3 = $5.40
Question 1 of 10
If there are 8 successful outcomes in a sample with a size of 25, what is the
sample proportion?
O A. 0.96
O B. 0.76
O C. 0.32
D. 0.52
SUBMIT

Answers
Answer: 0.32
Step-by-step explanation:

Word Problems Involving Real Numbers (Rational Numbers)
Solve for the following. Show your solution.
1. Paul spent 3
1/2
hours doing her assignment. Lorence did his assignment for
1 and 2/3 times as many hours as Paul did. How many hours did Lorence spend doing
3
his assignment?
2.
How many thirds are there in six-fifths?
3.
Hanna donated 2/5
of her monthly allowance to the landslide survivors. If her
monthly allowance is 500 aed, how much did she donate?
i will give brainliest if you answers fast
Answers
You are not going out of the same time for the same thing
Step-by-step explanation:
Uhgvhddfd dtcgxgstdd fhfgyfeywc
Gjufchhjjjjujch
yo anwser this as well

Answers
Answer:
3^8
Step-by-step explanation:
please mark me as brainlest to all questions please
What is the vertex of the graph of this equation y=-4x2 - 16x - 12?
Answers
Answer:
(-2,4)
I just turned it in it was right
Step-by-step explanation:
PLEASE MARK BRAINLIEST
someone on this god forsaken planet help me

Answers
Answer: Lol
B (-8,-5)
D (-10,-4)
C (-8,3)
Step-by-step explanation:
Cindy lost 47 pounds while on a diet. She now weighs 144 pounds. Write and solve an equation to find her initial weight.
Answers
Answer:
191
Step-by-step explanation:
47+144=191
Answer:
equation: 144+ 47= 191
Step-by-step explanation:
The price received for a bicycle is given by the equation b = 100 – 10x2, where x is the number of bicycles produced, in millions.
It costs the company $60 to make each bicycle.
What is the profit function for the company?
P = –10x2 – 60x + 100
P = –10x3 + 40x
P = – 10x2 + 40
Answers
Answer:
B
Step-by-step explanation:
What is the volume of this rectangular prism?
2/5cm
2/5cm
2/5cm
___cm3

Answers
Answer:
8/125cm3
Step-by-step explanation:
A=lxwxh
A=2/5 x 2/5 x 2/5
A=8/125cm
I hope this helps <3
What is the domain function of -3(x-5)+8
Answers
↝ Quadratic Function has the domain of all real numbers. (Even not given the specific domain.)
↝ The equation \(y=-3(x-5)+8\) is a parabola with (5,8) as a vertex. We call the equation \(y=a(x-h)^2+k\) as vertex equation.
The domain of -3(x-5)+8 is all set of real numbers.
↝ Interval Notation ↝
Since the domain of the equation is set of all real numbers.
Therefore, the domain is x ∈ R or (-∞,∞) or -∞<x<∞
There of them work. Recall that the domain of quadratic function is all set of real numbers.
solve pls brainliest

Answers
Answer:
20%
Step-by-step explanation:
12 / 60 = 0.2
0.2 x 100 = 20
20%
(% = Part / Whole × 100)
A store buys 4 sweaters for $20 and sells them for $136. How much profit does the store make per sweater?
Answers
Answer:
The profit per sweater is 29 dollars.
Step-by-step explanation:
First find the total profit.
136 - 20
116 for all 4 sweaters
Now divide by 4 since there are 4 sweaters to find the profit per sweater.
116/4
29
The profit per sweater is 29 dollars.
Mr. Adams has poster paper that is 10 3/4 feet long. He wants to make sheets that are 1/4 of a foot long to make paper airplanes. How many sheets can he make?
Answers
Answer:
43
Step-by-step explanation:
divide 10 3/4 by 1/4
suppose that ann selects a ball by first picking one of two boxes at random and then selecting a ball from this box. the first box contains three orange balls and four black balls, and the second box contains seven orange balls and four black balls. what is the probability that ann picked a ball from the second box if she has selected an orange ball? (enter the value of the probability in decimal format and round the final answer to two decimal places.)
Answers
The probability that Ann picked a ball from the second box given that she selected an orange ball is 0.56 or 56% (rounded to two decimal places).
We can use Bayes' theorem to calculate the probability that Ann picked a ball from the second box given that she selected an orange ball.
Let A be the event that Ann selected an orange ball, and B be the event that Ann picked a ball from the second box. We want to find P(B|A), the probability that Ann picked a ball from the second box given that she selected an orange ball.
We know that there are two boxes, each with a probability of 1/2 of being selected. The probability of selecting an orange ball from the first box is 3/7, and the probability of selecting an orange ball from the second box is 7/11. Therefore, the probability of selecting an orange ball overall is:
P(A) = P(A|B)P(B) + P(A|B')P(B')
= (7/11)(1/2) + (3/7)(1/2)
= 25/42
Now we can use Bayes' theorem:
P(B|A) = P(A|B)P(B)/P(A)
= (7/11)(1/2)/(25/42)
= 14/25
Therefore, the probability that Ann picked a ball from the second box given that she selected an orange ball is 0.56 or 56% (rounded to two decimal places).
Learn more about Bayes' theorem
https://brainly.com/question/29598596
#SPJ4
HELP ME PLEASE
7. When Mrs. Santo lived in China, temperature was measured in Celsius. She constantly had to convertir
Celsius to Fahrenheit until she started learning Celsius temperatures and how warm they are.
The formula to convert from Celsius to Fahrenheit is F = = C) + 32
The mean temperature for one month was 34°C and the standard deviation was 2.27.C. Applying what
know about multiplying by a constant and adding a constant, what was the mean and standard deviation
Fahrenheit? Be sure to show your work for both the mean and the standard deviation.

Answers
Answer:
Mean: \(93.2\; \rm ^{\circ} F\).
Standard deviation: \(4.086\; \rm ^{\circ} F\).
Step-by-step explanation:
Consider a random variable \(X\) with mean \(\overline{X}\) and variance \({\rm Var}(X)\).
If a random variable \(Y\) is obtained by linearly transforming \(X\) for some constants \(m \ne 0\) and \(b\), then the mean of \(Y\!\) would be:
\(\overline{Y} = m\, \overline{X} + b\).
\(\mathrm{Var}(Y) = m^{2} \, \mathrm{Var}(X)\).
The standard deviation of a random variable is the square root of its variance. Therefore, the standard deviation of \(Y\) would be:
\(\begin{aligned}\mathrm{SD}(Y) &= \sqrt{\mathrm{Var}(Y)} \\ &= \sqrt{m^{2}\, \mathrm{Var}(X)} \\ &= m\, \sqrt{\mathrm{Var}(X)} \\ &= m\, \mathrm{SD}(X)\end{aligned}\).
In this question, the random variable \(F\) is obtained by linearly transforming \(C\) using the constants \(m = (9/5)\) and \(b = 32\). That is:
\(F = (9/5)\, C + 32\).
It is given that mean \(\overline{C} = 34\) while standard deviation \(\mathrm{SD}(X) = 2.27\). The mean and standard deviation of \(F\) obtained from the linear transformation would be:
\(\begin{aligned}\overline{F} &= m\, \overline{C} + b \\ &= (9/5) \times 34 + 32\\ &= 93.2\end{aligned}\).
\(\begin{aligned}\mathrm{SD}(F) &= m\, \mathrm{SD}(C) \\ &= (9/5) \times 2.27 = 4.086\end{aligned}\).
Thus, when measured in degrees Fahrenheit, the corresponding mean would be \(93.2\; \rm ^{\circ} F\) and and standard deviation would be \(4.086\; \rm ^{\circ} F\).
USE F= 7, M= 0 AND L = 5. PLEASE SHOW ALL STEPS AND SOLVE
ACCORDINGLY
\[ l y^{\prime \prime}+m y^{\prime}+f y=e^{l x} ; y(0)=m, y^{\prime}(0)=f \] Where, \( f, m \), and \( l \) are the number of letters in your first name, middle name, and last name respectively. (Note
Answers
Given the values (f = 7), (m = 0), and (l = 5) (corresponding to the number of letters in my first name, middle name, and last name, respectively), we can rewrite the differential equation as follows:
[5y^{\prime \prime} + 0y^{\prime} + 7y = e^{5x}, \quad y(0) = 0, \quad y^{\prime}(0) = 7.]
To solve this second-order linear homogeneous ordinary differential equation with constant coefficients, we first find the characteristic equation by assuming a solution of the form (y = e^{rx}). Substituting this into the differential equation, we get:
[5r^2 + 7 = 0.]
Solving this quadratic equation for (r), we have:
[r^2 = -\frac{7}{5}.]
Taking the square root of both sides, we obtain:
[r = \pm i\sqrt{\frac{7}{5}}.]
Since the roots are complex, we have two complex conjugate solutions: (r_1 = i\sqrt{\frac{7}{5}}) and (r_2 = -i\sqrt{\frac{7}{5}}).
The general solution to the homogeneous equation is given by:
[y_h(x) = c_1 e^{r_1 x} + c_2 e^{r_2 x},]
where (c_1) and (c_2) are arbitrary constants.
Next, we need to find a particular solution to the non-homogeneous equation. Since the right-hand side of the equation is (e^{5x}), we can assume a particular solution of the form (y_p(x) = Ae^{5x}), where (A) is a constant to be determined.
Substituting this into the differential equation, we have:
[5(5^2Ae^{5x}) + 7Ae^{5x} = e^{5x}.]
Simplifying, we get:
[25Ae^{5x} + 7Ae^{5x} = e^{5x}.]
Combining like terms, we obtain:
[32Ae^{5x} = e^{5x}.]
Dividing both sides by (e^{5x}), we find:
[32A = 1.]
Therefore, (A = \frac{1}{32}).
Hence, the particular solution is (y_p(x) = \frac{1}{32}e^{5x}).
The general solution to the non-homogeneous equation is the sum of the general solution to the homogeneous equation and the particular solution:
[y(x) = y_h(x) + y_p(x).]
Substituting the values of (r_1), (r_2), and (A), we have:
[y(x) = c_1 e^{i\sqrt{\frac{7}{5}}x} + c_2 e^{-i\sqrt{\frac{7}{5}}x} + \frac{1}{32}e^{5x}.]
To determine the constants (c_1) and (c_2), we use the initial conditions (y(0) = 0) and (y'(0) = 7).
From (y(0) = 0):
[c_1 + c_2 + \frac{1}{32} = 0.]
From (y'(0) = 7):
[i\sqrt{\frac{7}{5}}c_1 - i\sqrt{\frac{7}{5}}c_2 + 5\cdot \frac{1}{32} = 7.]
Simplifying the equations, we get:
[c_1 + c_2 = -\frac{1}{32},]
[i\sqrt{\frac{7}{5}}c_1 - i\sqrt{\frac{7}{5}}c_2 + \frac{5}{32} = 7.]
Adding the two equations, we find:
[2c_1 = 7 - \frac{1}{32}.]
Hence,
[c_1 = \frac{7}{2} - \frac{1}{64} = \frac{111}{32}.]
Substituting this value of (c_1) into the first equation, we obtain:
[\frac{111}{32} + c_2 = -\frac{1}{32}.]
Simplifying, we find:
[c_2 = -\frac{1}{32} - \frac{111}{32
Learn more about differential equation here
https://brainly.com/question/33433874
#SPJ11
Samantha has 67 cents in her pocket. Write two coin combinations she could have that would equal the same amount
Answers
she could have that would equal the same amount.
Answer:
Given
Samantha have 67 cents
penny
1 cent
$0.01
nickel
5 cents
$0.05
dime
10 cents
$0.10
quarter
25 cents
$0.25
6 dimes, 1 nickels and 2 pennies
makes 67 cents
2 quarters, 2 nickels and 2 pennies
makes 67 cents.

For a positively skewed distribution with a mode of x = 31 and a mean of 36, the median is most probably?
Answers
According to the question the median is most probably less than 36.
For a positively skewed distribution, the mode is the value that occurs most frequently, the mean is the average value, and the median is the middle value when the data is arranged in ascending order.
Given that the mode is \(\(x = 31\)\) and the mean is \(\(36\),\) we can infer that the majority of the data is clustered towards the left (lower values) and there are some relatively high values that pull the mean to the right.
Since the distribution is positively skewed, the median is expected to be lower than the mean. This is because the presence of outliers or higher values on the right side of the distribution affects the mean more than the median.
Therefore, the median is most probably less than 36.
To know more about median visit -
brainly.com/question/33815261
#SPJ11
Which of the following expressions can you multiply using the FOIL Method? Check all that apply. k12
2x(x2+8x−2)
(x−3)(x2+9x−1)
(5x+1)(x+3)
(x−c)(x−d)
Answers
Options (C) and (D) are the correct options.
FOIL method of multiplication: FOIL method of multiplication is applicable for the expressions in the
form of (a - b)(c - d).
Here, a and c are the FIRST terms
a and d are the OUTER terms
b and c are the INNER terms
b and d are the LAST terms
Multiply all FIRST, OUTER, INNER and LAST terms and add them.
(a - b)(c - d) = a.c + a(-d) + (-b)c + (-b)(-d)
= ac - ad - bc + bd
= ac - (ad + bc) + bd
Therefore, expressions given in options (C) and (D) are the correct options.
Learn more about the FOIL method of multiplication here,
https://brainly.com/question/13984641?referrer=searchResults
day weight (ounces) monday 23 22 23 24 tuesday 23 21 19 21 wednesday 20 19 20 21 thursday 18 19 20 19 friday 18 20 22 20 what is the mean of the sampling distribution of sample means when this process is in control?
Answers
The value of the required mean of the sampling distribution of sample means is approx. 21 ounces when this process is in control.
Sample mean: The arithmetic mean of the values of the variables in the sample. If the samples are drawn from probability distributions with a common expected value, the sample mean is an estimate of that expected value.
Sample means for all days using formula,
Monday = (23+22+23+24)/4 = 23
Tuesday = (23+21+19+21)/4 = 21
Wednesday = (20+19+20+21)/4 = 20
Thursday = (18+19+20+19)/4 = 19
Friday = (18+20+22+20)/4 = 20
We have to calculate the mean of sampling distribution of sample means.
Mean of the sampling distribution of sample means = Sum of sample means of all days / Number of days
= (23+21+20+19+20)/5
= 20.6 = 21 ounces
Hence, the required mean is approx. 21 ounces.
To learn more about Sampling distribution of sample means , refer:
https://brainly.com/question/26952915
#SPJ4
The measures of the angles of a triangle are shown in the figure below. Solve for x.

Answers
Answer:
x=17 degrees
Step-by-step explanation:
All 3 angles = 180 degrees
So 90 + 54 + (x+19) = 180
Combine like terms
163 + x = 180
Subtract 163 from both sides
x = 180-163
x = 17
I need help bcuz I'm dum

Answers
Answer: 697
Step-by-step explanation:
(9)(3)(9)(3)−(12)(3)+4
=(27)(9)(3)−(12)(3)+4
=(243)(3)−(12)(3)+4
=729−(12)(3)+4
=729−36+4
=693+4
=697
How I can answer this question, NO LINKS, if you answer correctly I will give u brainliest!
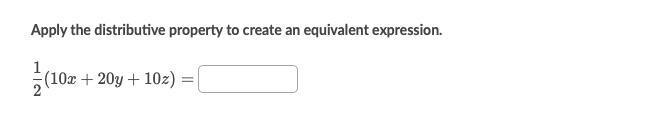
Answers
Answer:
5x+10y+5z
Step-by-step explanation:
hope this helped luis also other person is correct
Which of the following is not a factor of the binomial 7x^2-28x?
1. x-4
2.x
3.7
4.-4