Lengths (mm) Frequency 140 - 154 1 155 - 169 16 170 - 184 71 185 - 199 108 200 - 214 83 215 - 229 18 230 - 244 3
Answers
The frequency distribution appears to be centered around 192 mm, with most of the observations falling within the range of 170-214 mm.
This appears to be a frequency distribution table for the lengths (in millimeters) of some objects or organisms. The table shows the number of observations (frequency) that fall within each interval of length.
To summarize the information in the table, we can calculate some descriptive statistics:
Range: The range of lengths is the difference between the maximum and minimum values. In this case, the minimum length is 140 mm and the maximum length is 244 mm, so the range is 244 - 140 = 104 mm.
Mean: The mean length is the average of all the observations. To calculate the mean, we can use the midpoint of each interval as an estimate of the values in that interval.
For example, the midpoint of the first interval (140-154) is (140+154)/2 = 147, so we can assume that the one observation in that interval is approximately equal to 147 mm. Then, we can multiply each midpoint by its corresponding frequency, add up the products, and divide by the total number of observations.
This gives:
mean = (1147 + 16162 + 71177 + 108192 + 83207 + 18222 + 3*237) / (1+16+71+108+83+18+3) = 187.02 mm
Median: The median length is the middle value when the observations are arranged in order. To find the median, we can add up the frequencies until we reach the midpoint of the total (which is (1+16+71+108+83+18+3)/2 = 160).
Then, we can find the interval that contains the 160th observation and calculate the midpoint of that interval. In this case, the interval is (185-199), which contains 108 observations, so the median is (185+199)/2 = 192 mm.
Mode: The mode is the value or interval with the highest frequency. In this case, the interval with the highest frequency is (185-199), which has a frequency of 108, so the mode is the midpoint of that interval, which is 192 mm.
Standard deviation: The standard deviation is a measure of the spread or variability of the observations around the mean. To calculate the standard deviation, we can use the formula:
\(sd = sqrt( (1/N) * sum( (x_i - mean)^2 ) )\)
where N is the total number of observations, x_i is the ith observation, and mean is the mean of all the observations. This gives:
\(sd = sqrt( (1/300) * ( (1-147)^2 + (16-162)^2 + ... + (3-237)^2 ) )\)= 21.82 mm
These statistics can help us to understand the distribution of lengths and to compare it to other distributions. For example, the mean and median are relatively close to each other, indicating that the distribution is roughly symmetric.
The mode is also close to the mean and median, which further supports this conclusion. The standard deviation is moderate, suggesting that there is some variability in the lengths, but not extreme. Overall, the distribution appears to be centered around 192 mm, with most of the observations falling within the range of 170-214 mm.
Learn more about frequency distribution at
brainly.com/question/28569100
#SPJ4
Related Questions
Hudson bay wants price MSRP 59.99 acquire sheets for
22.99 what is markup on cost percentage
Answers
The markup on cost percentage for Hudson Bay's acquisition of sheets priced at MSRP 59.99 for 22.99 is 61.68%.
To calculate the markup on cost percentage, we can use the following formula:
Markup on Cost Percentage = ((Selling Price - Cost Price) / Cost Price) x 100
In this case, the cost price of the sheets is 22.99, and the selling price (MSRP) is 59.99. Plugging these values into the formula, we get:
Markup on Cost Percentage = ((59.99 - 22.99) / 22.99) x 100
Markup on Cost Percentage = (37 / 22.99) x 100
Markup on Cost Percentage = 1.6103 x 100
Markup on Cost Percentage = 61.68%
Therefore, Hudson Bay's markup on cost percentage for acquiring sheets priced at MSRP 59.99 for 22.99 is 61.68%.
To know more about cost percentage refer here:
https://brainly.com/question/26080842#
#SPJ11
TRUE/FALSE. in a poisson distribution, the probability of success may vary from trial to trial.
Answers
The statement is false because in a Poisson distribution, the probability of success does not vary from trial to trial.
The Poisson distribution is a discrete probability distribution that describes the number of times an event occurs in a fixed time interval or spatial region, given the average rate of occurrence and assuming that the events are independent and random.
The Poisson distribution has only one parameter, λ, which represents the average rate of occurrence of the event.
The probability of observing k events in the interval is given by the Poisson probability mass function:
P(k) = (e^(-λ) * λ^k) / k!
where e is the base of the natural logarithm, and k is a non-negative integer.
The Poisson distribution assumes that the probability of observing an event at any given point in time or space is constant, and that the events are independent of each other.
To know more about Poisson distribution refer here:
https://brainly.com/question/30388228#
#SPJ11
A bag contain 3 red candy and 5 green candy
jackl take one a t random and eat it
what i the probality of him getting 2 red one
Answers
The probability of Jack taking 2 red candies is 3/28.
What do you mean by a union in probability?
The letter "U" (union) stands for "or." Specifically, P(AB) represents the probability of that event A or event B occurring. The sample points that are present in both event A and event B must be counted in order to determine P(AUB).
The new probability set made up of all the elements from both sets is created when two sets are joined. When two sets intersect, a new set is created that includes every element from both sets.
Solution Explained:
Given in the question,
A bag contains 3 red and 5 green candies.
Total possibilities is 3 + 5 = 8
Jack takes a candy at random and eats it
A/Q there are 3 red candies out of 8, the probability is given by,
P(R) = 3/8
Now there are 2 red candies out of 7, so the probability is given by,
P(R') = 2/7
The probability of both events is given by,
P(2R) = P(R) × P (R') = 3/8 × 2/7 = 3/28
Therefore, the probability of Tim taking 2 red candies is P(2R) = 3/28
To learn more about the union in probability, use the link given
https://brainly.com/question/24527389
#SPJ4
Plot the points and name the figure you obtain also find its area (-1,-2),(1,0),(-1,2),(-3,0)
Answers
Answer:
i plot the points and it is a sqaure
Find the equation of the parabola with the given x-intercepts and point on the graph. Use y = a(x-p)(x-q).
2. x-int: (-4,0) , (-10, 0)
P (-6,-12)
Answers
Answer:
y = 1.5(x + 4)(x + 10)=========================
Givenx- intercepts (-4, 0) and (-10, 0),Point P (- 6, - 12).SolutionThe given translates as:
p = - 4, q = - 10, x = - 6, y = - 12Use given x - intercepts to get the equation:
y = a(x + 4)(x + 10)Use the coordinates of P to find the value of a:
- 12 = a(-6 + 4)(-6 + 10)- 12 = a*(-2)*4- 12 = - 8aa = - 12 / - 8a = 1.5The equation of this parabola is:
y = 1.5(x + 4)(x + 10)Answer:
\(\textsf{Intercept form}: \quad y=\dfrac{3}{2}(x+4)(x+10)\)
\(\textsf{Standard form}: \quad y=\dfrac{3}{2}x^2+21x+60\)
Step-by-step explanation:
\(\boxed{\begin{minipage}{6 cm}\underline{Intercept form of a quadratic equation}\\\\$y=a(x-p)(x-q)$\\\\where:\\ \phantom{ww}$\bullet$ $p$ and $q$ are the $x$-intercepts. \\ \phantom{ww}$\bullet$ $a$ is some constant.\\\end{minipage}}\)
If the x-intercepts are (-4, 0) and (-10, 0) then:
p = -4q = -10Substitute the values of p and q into the formula:
\(\implies y=a(x-(-4))(x-(-10))\)
\(\implies y=a(x+4)(x+10)\)
To find a, substitute the given point on the curve P (-6, -12) into the equation:
\(\implies -12=a(-6+4)(-6+10)\)
\(\implies -12=a(-2)(4)\)
\(\implies -12=-8a\)
\(\implies a=\dfrac{-12}{-8}\)
\(\implies a=\dfrac{3}{2}\)
Substitute the found value of a into the equation:
\(\implies y=\dfrac{3}{2}(x+4)(x+10)\)
Expand to write the equation in standard form:
\(\implies y=\dfrac{3}{2}(x^2+14x+40)\)
\(\implies y=\dfrac{3}{2}x^2+21x+60\)
saleswoman earns 9% commission on all the merchandise that she sells. Last month she sold $8000 worth of merchandise. How much commission (in dollars) did she earn last month?
Answers
Answer:
8720
Step-by-step explanation:
If it's anything like compound / simple interest here's how to do it:
The multiplier for +9% is 1.09
8000 x 1.09 = 8720
Henry deposited his savings in the neighborhood bank. The bank paid an interest of 8% compounded quarterly. How much had Henry deposited if he received $13,299. 23 after 5 years? Round your answer to the nearest dollar
Answers
Henry had deposited approximately $8,000.32 if he received $13,299.23 after 5 years. Rounded to the nearest dollar, the answer is $8,000.To solve this problem, we can use the formula for compound interest:
\($$ A = P \left(1 + \frac{r}{n}\right)^{nt} $$\)
where A is the amount after t years, P is the principal (the amount deposited), r is the annual interest rate, n is the number of times the interest is compounded per year, and t is the number of years.
In this case, we have:
A = $13,299.23
r = 0.08 (8%)
n = 4 (quarterly compounding)
t = 5 years
We can rearrange the formula to solve for P:
\(P = \frac{A}{(1 + \frac{r}{n})^(nt) }\)
Plugging in the values, we get:
\(P = \frac{ $13,299.23}{(1 + \frac{0.08}{4} ) ^ {(4*5)} }\)
P ≈ $8,000.32
Therefore, Henry had deposited approximately $8,000.32 if he received $13,299.23 after 5 years. Rounded to the nearest dollar, the answer is $8,000.
To know more about deposits
brainly.com/question/15841366
#SPJ4
Please help I need statements and reasonings

Answers
Answer:
Step-by-step explanation:
angle 3 is about half of the measure of angle 4. You can easily see that angle 4 is a right angle, then next to it, angles 3 and 5 make up a right angle together, seemingly dividing the right angle into two halves. So, angle 3 is about half of angle 4
I hope this helps you! Good luck on the test/homework!
i need help please branliest to who gets it right

Answers
The kite is about 16.5 yards above the edge of the pond.
How to find the height of the kite?You are flying a dragon kite. It's connected to 36 yards string. The kite is directly above the end of the pond. The edge of the pond is 32 yards where the kite is tied to the ground.
Therefore, the height of the kite above the ground can be calculated as follows:
This situation form a right angle triangle. Hence, using Pythagoras's theorem,
Therefore,
h² = 36² - 32²
h² = 1296 - 1024
h = √272
h = 16.4924225025
Hence, the height of the kite is 16.5 yards.
learn more on right triangle here: brainly.com/question/28975129
#SPJ1
х
f(x)
Analyze the table of values for the continuous function,
f(x), to complete the statements.
A local maximum occurs over the interval
A local minimum occurs over the interval
-3
-16
-2
-1
-1
2
0
-1
1
-4
N
-1
Answers
Answer: the answer is
(-2,0)
(0,2)
Answer:
The answer is
( -2, 0 )
(0, 2 )
Step-by-step explanation:
I just took the test and got it right
Hopefully this helps you
pls mark brainlest
find the radian measure of an angle at the center of a circle with radius 77.0 cm that intercepts an arc length of 128 cm
Answers
The radian measure of the angle at the center of the circle is approximately 1.6623 radians.
We are given that the radius of the circle is 77.0 cm and the length of the intercepted arc is 128 cm. We need to find the radian measure of the angle at the center of the circle.
To solve this problem, we use the formula relating the angle at the center of a circle, the radius of the circle, and the arc length intercepted by the angle.
The formula is given byθ = s/rwhereθ = angle at the center of the circle in radians s = arc length intercepted by the angle r = radius of the circle Substituting the given values, we getθ = 128/77.0 = 1.6623 radians (rounded to four decimal places)
Therefore, the radian measure of the angle at the center of the circle is approximately 1.6623 radians.
For more such questions on radian measure
https://brainly.com/question/19758686
#SPJ8
When studying radioactive material, a nuclear engineer found that over 365 days, 1,000,000 radioactive atoms decayed to 974,728 radioactive atoms, so 25,272 atoms decayed during 365 days a. Find the mean number of radioactive atoms that decayed in a day b. Find the probability that on a given day, 50 radioactive atoms decayed
Answers
a) The mean number of radioactive atoms that decayed in a day is approximately 69.28 atoms. and b) the probability that on a given day, 50 radioactive atoms decayed is approximately 2.314685e-47.
a. To find the mean number of radioactive atoms that decayed in a day, we can divide the total number of atoms decayed over 365 days by the number of days:
Mean number of radioactive atoms decayed per day = Number of atoms decayed / Number of days
Mean number of radioactive atoms decayed per day = 25,272 atoms / 365 days
Mean number of radioactive atoms decayed per day ≈ 69.28 atoms
Therefore, the mean number of radioactive atoms that decayed in a day is approximately 69.28 atoms.
b. To find the probability that on a given day, 50 radioactive atoms decayed, we can use the Poisson distribution. The Poisson distribution is often used to model the number of events occurring in a fixed interval of time or space.
The formula for the Poisson distribution is:
P(X = k) = \((e^(-λ) * λ^k) / k!\)
Where:
P(X = k) is the probability that k events occur,
e is Euler's number, approximately 2.71828,
λ is the average number of events occurring in the given interval,
k is the number of events we are interested in.
In this case, the average number of radioactive atoms decayed in a day is approximately 69.28 atoms (calculated in part a). Therefore, λ = 69.28.
Substituting the values into the Poisson distribution formula:
P(X = 50) =\((e^(-69.28) * 69.28^50)\) / 50!
Calculating \(e^(-69.28):\)
\(e^(-69.28)\) ≈ 2.67048178576e-31
Calculating \(69.28^50:\)
\(69.28^50\) ≈ 2.64267020807e+80
Calculating 50! (factorial of 50):
50! ≈ 3.04140932017e+64
Substituting these values back into the formula:
P(X = 50) ≈ (2.67048178576e-31 * 2.64267020807e+80) / 3.04140932017e+64
P(X = 50) ≈ 2.314685e-47
Therefore, the probability that on a given day, 50 radioactive atoms decayed is approximately 2.314685e-47.
know more about mean number
https://brainly.com/question/21800892
#SPJ11
Of the 100 snakes on display at the nature center, 30% were venomous. How many of the 100 snakes were venomous?
HURRY PLEASE
Answers
Answer:
There are 30 venomous snakes.
Step-by-step explanation:
Since its 30% you can assume that its a total of 100%. So, 100 snakes would be 100%. So the total of venomous snakes are 30 total snakes. Hope this helped!! :D
Question 4 (0.5 points)
Which expression is equivalent to 42x + 6?
6(7x + 6)
0617x + 1)
7(6x + 6)
2(40x + 8)
Answers
Find the inverse of each function. f (x) = 3/x − 2 + 1
Answers
Hope it helps:)
wILL GIVE YOU BRANLIEST, JUST PLEASE ANSWER ANYONE.

Answers
I hope this helps you!


Which transformations of quadrilateral PQRS would result in the image of the quadrilateral being located only in the first quadrant of the coordinate plane?
Select each correct answer.
A. a translation right 4 units
B. a reflection across x = 4
C. a reflection across y = −x
D. a rotation of 90˚ counterclockwise about vertex Q
E. a reflection across x=3, then a translation up 8 units
F. a reflection across the x-axis, then a translation up 13 units

Answers
Answer:
E
Step-by-step explanation:
The first quadrant is the top-right one
If a point is in the first quadrant, the x- and y-values of the point are both positive
Let's go through the one by one.
A) Translating the quadrilateral right 4 units will make the new S to be \((-3+4, -7)=(1, -7)\), which is not in the first quadrant.
B) Reflection the quadrilateral across \(x=4\) will not change the y-value of any points. So, the new S will stay below the x-axis, and thus will never be in the first quadrant, because it will always have a negative y-value.
C) This one is tricky. We can prove(the proof is just taking cases of which quadrant) that if a point is in the second or fourth quadrant, it's reflection across the line \(y=-x\) will always be in the same quadrant it started in(i.e. reflect a point in the second quadrant, you get a point in the second quadrant). We know that P is in the second quadrant, so the new P will also be in the second quadrant. Therefore, the new quadrilateral will not be entirely in the first quadrant.
D) We intuitively(and can prove) that because R is right underneath Q, the new R will be directly to the left of Q, with the same distance as Q to original R. So, the new R will be \((-10, 12)\) using above method. This point is not in the first quadrant.
E) We know intuitively(and can prove) that a reflection across the line \(x=3\) will make the entire quadrilateral in the first and fourth quadrant. However, When we translate up, the new S, the lowest point on the quadrilateral, will be above the x-axis, making all the points in the first quadrant! Therefore, E works.
F) When we reflect across the x-axis, any points in the second quadrant go to the third quadrant. So, the new P will be in the third quadrant. However, when we translate up 13 units, the new P will go to the second quadrant. It will never cross the y-axis, and will always have a negative x-coordinate. Therefore, P will not be in the first quadrant.
Summing up the cases that work, we get that \(\boxed{E}\) is the only answer.
The transformations of quadrilateral PQRS which would result in the image of the quadrilateral being located only in the first quadrant of the coordinate plane is:
E. A reflection across x=3, then a translation up 8 unitsWhat is a Quadrant?This refers to the axis of a two dimensional Cartesian system which is one side out of four quarters of a circle or given shape.
From the given image, we can see that the first quadrant is at the top.
With this, we can see that the transformation which would make the quadrilateral PQRS to be in the first quadrant is a reflection across x=3, then a translation up 8 units.
This is because when we translate up, then we can see that the x-y values of the point are positive and which would make the translation up 8 points.
Read more about coordinate plane here:
https://brainly.com/question/18168162
PLEASEEE HELP ILL GIVE BRAINLIEST btw there are 2 attachments so u could see all the answer choices

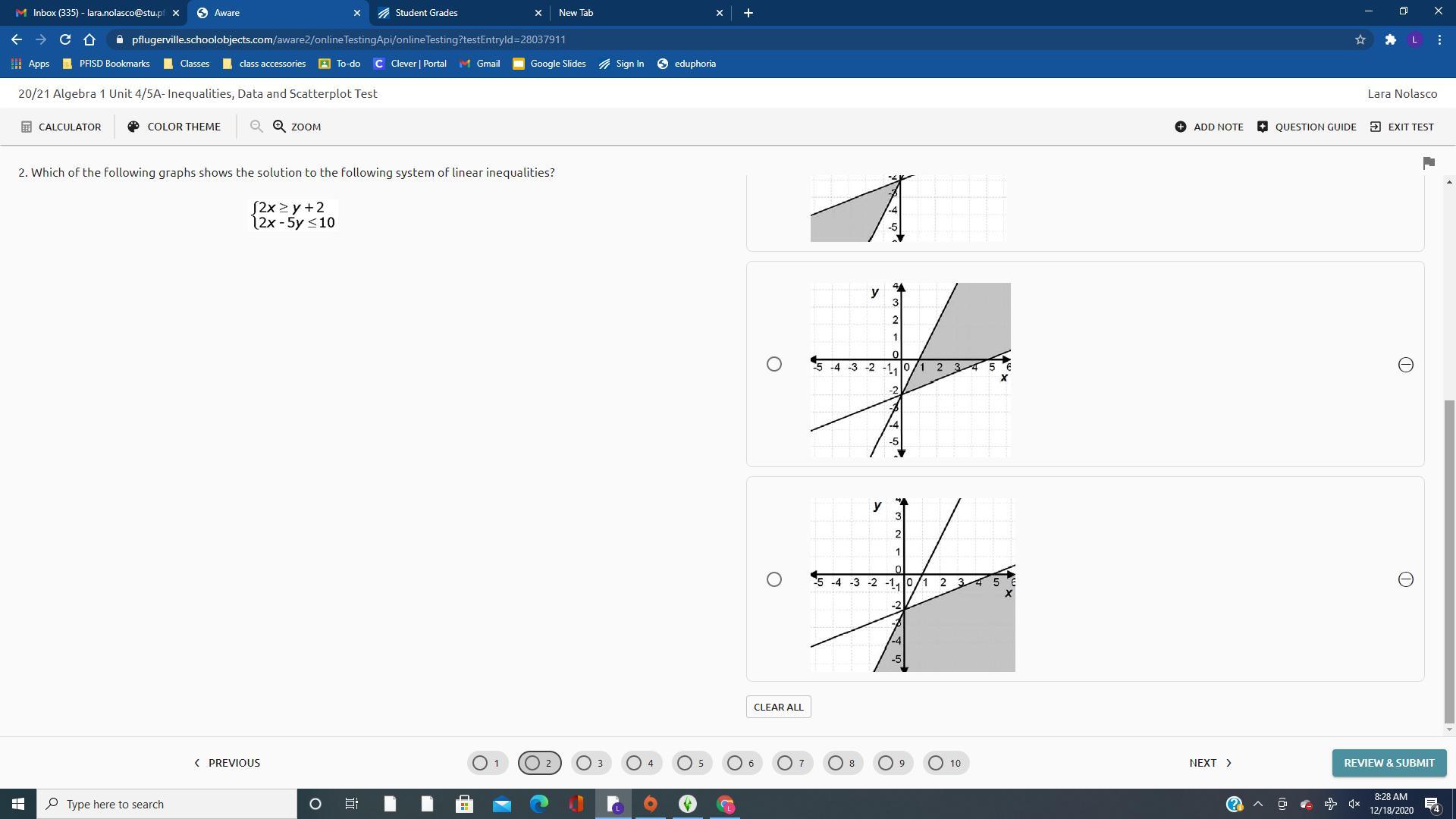
Answers
Answer:
1) C
Step-by-step explanation:
Step 1)
First we have to plot ↓
2x ≥ y + 2
And that looks like Image 1
Step 2)
Second we have to plot ↓
2x - 5y ≤ 10
and that looks like Image 2


a^2m+4m/a^2+4 reduce
m
m^2
2m
Answers
Answer:
just m
Step-by-step explanation:
You and your friend are going into business mowing lawns. If you can mow a 1 acre lawn in 35 minutes and your friend can mow a 1 acre lawn in 50 minutes, how long will it take for you to mow 6 acres together? How much will you make if your combined rate is $20/hour?
Answers
Answer:
80$ (maybe 85)
Step-by-step explanation:
combined rate =20$/hour
It can take 85 minutes for you and your friend to mow 2 acres. 35+50=85. So 85*3 (because 6/2=3) is the number of minutes you work. 255 minutes. So 4.25 hours. If you are only being paid for hours, then you will make $80. If you are being paid the extra minutes the $85. I believe that the answer you should pick is $80.
Answer:
$41.18
Step-by-step explanation:
35/50 = 0.7
Therefore, in the time it takes you mow 1 acre, your friend mows 0.7 acres
Therefore, for every 35 minutes = 1 + 0.7 = 1.7 acres are mowed by you and your friend combined.
⇒ 1.7 ÷ 35 = 0.04857142... acres mowed every minute
⇒ 6 ÷ 0.04857142... = 123.5294118... minutes to 6 acres
Therefore, it takes 35/17 hours for you and your friend to mow 6 acres
If your rate is $20 per hour, then 35/17 x 20 = $41.18
The maintenance crew of a hotel has to monitor the temperature of the hotel pool and hot tub. To enhance comfort, the management team requests that the mean pool temperature and the mean hot tub temperatures not differ by more than 15 degrees. To estimate the difference in these mean temperatures the maintenance crew selects a random sample of 8 times to check the hot tub temperature and a random sample of 10 times to check the pool temperature. Although the sample sizes are small, the distribution of temperature for the pool and for the hot tub does not show strong skewness or any outliers. The mean pool temperature is 86 degrees with a standard deviation of 3 degrees. The mean hot tub temperature is 101 with a standard deviation of 1.8 degrees. What is the correct 95% confidence interval for the true difference in the population means (hot tub – pool)? Use the conservative df.
Answers
Answer: Option D
Explanation: 100%

Parallelogram P was dilated to form parallelogram P prime. Parallelogram P has side lengths of 10 and x 3. Parallelogram P prime has side lengths of 20 and 8. What is the value of x? (Figures not drawn to scale. ).
Answers
The value of x is 1.
DilationDilation means the changing of the size of the object without changing the shape. The size of the object may be increased or decreased based on the scale factor.
Given
Dimension of parallelogram P 10 and x + 3.
Dimension of parallelogram P' 20 and 8.
To findThe value of x.
How to find the value of x?Lenght of P' = Dilation x Lenght of P
20 = Dilation x 10
Dilation = 2
Then
width of P' = Dilation x width of P
8 = 2 (x + 3)
4 = x + 3
x = 1
So the value of x is 1.
More about the Dilation link is given below.
https://brainly.com/question/2856466
Answer:
the value of x is 1
Step-by-step explanation:
Amani earns 41 dollars per week working part-time at a book store. She makes one dollar more for each book that she sells. The amount, A (in dollars), that
Amani earns in a week if she sells b books is given by the following.
A=41+b
How much does Amani earn in a week if she sells 18 books?
Answers
Amani earns 59 dollars in a week if she sells 18 books.
Amani earns a base amount of $41 per week for working part-time at the bookstore. In addition to that, she earns an extra dollar for each book she sells. The equation A = 41 + b represents her total earnings, where A represents the amount she earns and b represents the number of books she sells.
To find out how much Amani earns in a week if she sells 18 books, we substitute the value of b (18) into the equation:
A = 41 + 18
This simplifies to:
A = 59
Therefore, if Amani sells 18 books in a week, she will earn $59.
For more such questions on sells , Visit:
https://brainly.com/question/24951536
#SPJ11
alice has perfect substitutes preferences. she is indifferent between bundle (x = 20, y = 5) and bundle (x= 10, y = 30). what is her marginal rate of substitution for x with y? 0.4 -2.5 -0.4 2.5
Answers
The marginal rate of substitution for x with y for Alice with perfect substitutes preferences is 0.4.
To find the marginal rate of substitution (MRS), we can use the formula: MRS = change in y / change in x. In this case, we can use the two bundles given to find the change in x and y.
Change in x = 20 - 10 = 10
Change in y = 30 - 5 = 25
So, MRS = 25 / 10 = 2.5
However, since Alice has perfect substitutes preferences, she is willing to give up a smaller amount of one good for a larger amount of another good. This means that her MRS will be less than 1.
To find the MRS for x with y, we can simply take the reciprocal of the MRS for y with x:
MRS for x with y = 1 / MRS for y with x = 1 / 2.5 = 0.4
Therefore, the correct answer is 0.4.
For more similar questions on substitution :
brainly.com/question/4449154
#SPJ11
Which pair of terms are like terms in the expression 3x + 2 – x?
Answers
Answer:
3x and x
Step-by-step explanation:
because you can put them together to make 2x+2
Answer:
3x and -x
Step-by-step explanation:
Like terms are terms that are in the same form. So essentially, 3x and -x are both able to be added and subtracted from each other in this case.
what is 1.92 ÷ 32 ???
Answers
Therefore:
\(\frac{1.92}{32}=0.06\)
help which one is it

Answers
Answer:
I think it's 3 units to the left and 6 units down
Step-by-step explanation:
Hope I helped!
John and Pablo caught fish that have the lengths, in centimeters, listed below. 45, 44, 47, 49, 45, 47, 42, 39, 45, 42, 44 Which box-and-whisker plot correctly represents the data?
Answers
The options for the box and whisker plots aren't given ; however using technology, a box and whisker plot could be generated from the data.
Answer:
Step-by-step explanation:
Given :
45, 44, 47, 49, 45, 47, 42, 39, 45, 42, 44
Using technology, the box and whisker plot generated for the data is attached below.
The 5 - number summary is also given below :
Minimum: 39
Median: 45
First quartile: 42
Third quartile: 47
Interquartile Range: 5
Maximum: 49
Outliers: none

Answer:
Step-by-step explanation:
The distance from Mexico City, Mexico to Monterrey, Mexico is 931 kilometers. How far is this in miles? Round your answer to the nearest whole number. (1 mile = 1.6 kilometers)
Answers
Answer:
578
Step-by-step explanation:
divide the length value by 1.609
Find the x-intercept and y-intercept of the graph of the equation 2y = 3x - 6.
Answers
Given:
The equation is:
\(2y=3x-6\)
To find:
The x-intercept and y-intercept of the graph of the given equation.
Solution:
We have,
\(2y=3x-6\)
Substitute \(y=0\) to find the x-intercept.
\(2(0)=3x-6\)
\(0+6=3x\)
\(\dfrac{6}{3}=x\)
\(2=x\)
So, the x-intercept of the graph of the given equation is 2.
Substitute \(x=0\) to find the y-intercept.
\(2y=3(0)-6\)
\(2y=-6\)
\(y=\dfrac{-6}{2}\)
\(y=-3\)
So, the y-intercept of the graph of the given equation is -3.
Therefore, the x-intercept is 2 and the y-intercept is -3.
