.(10 points) In the following, A, B are real numbers. You do NOT need to find them to answer the questions below. (a) The possible POSITIVE rational roots of 3r³+ Ar2+Bz-14 are (b) The graph of y = 3a + Ar + Br-14 is shown below:
Answers
(a) Without the specific values of A and B, it is not possible to find the exact rational roots. (b) The given equation, y = 3a + Ar + Br - 14, represents a linear function with variables a and r.
(a) The possible positive rational roots of the polynomial 3r³ + Ar² + Bz - 14 are yet to be determined. The rational roots theorem states that if a rational root exists, it must be in the form of p/q, where p is a factor of the constant term (-14) and q is a factor of the leading coefficient (3). However, since the coefficients A and B are unknown, we cannot determine the rational roots without further information.
(b) The graph of this equation can be a straight line in the coordinate plane. The specific shape and position of the graph depend on the values of coefficients A and B, which are not provided in the question. Without the values of A and B, we cannot determine the exact characteristics of the graph, such as slope or intercepts. To analyze the graph further, it is necessary to have the values of A and B or additional information about the equation.
learn more about rational roots theorem here: brainly.com/question/30779768
#SPJ11
Related Questions
Can someone please solve these? Identify the segment bisect of XY. Then find XY
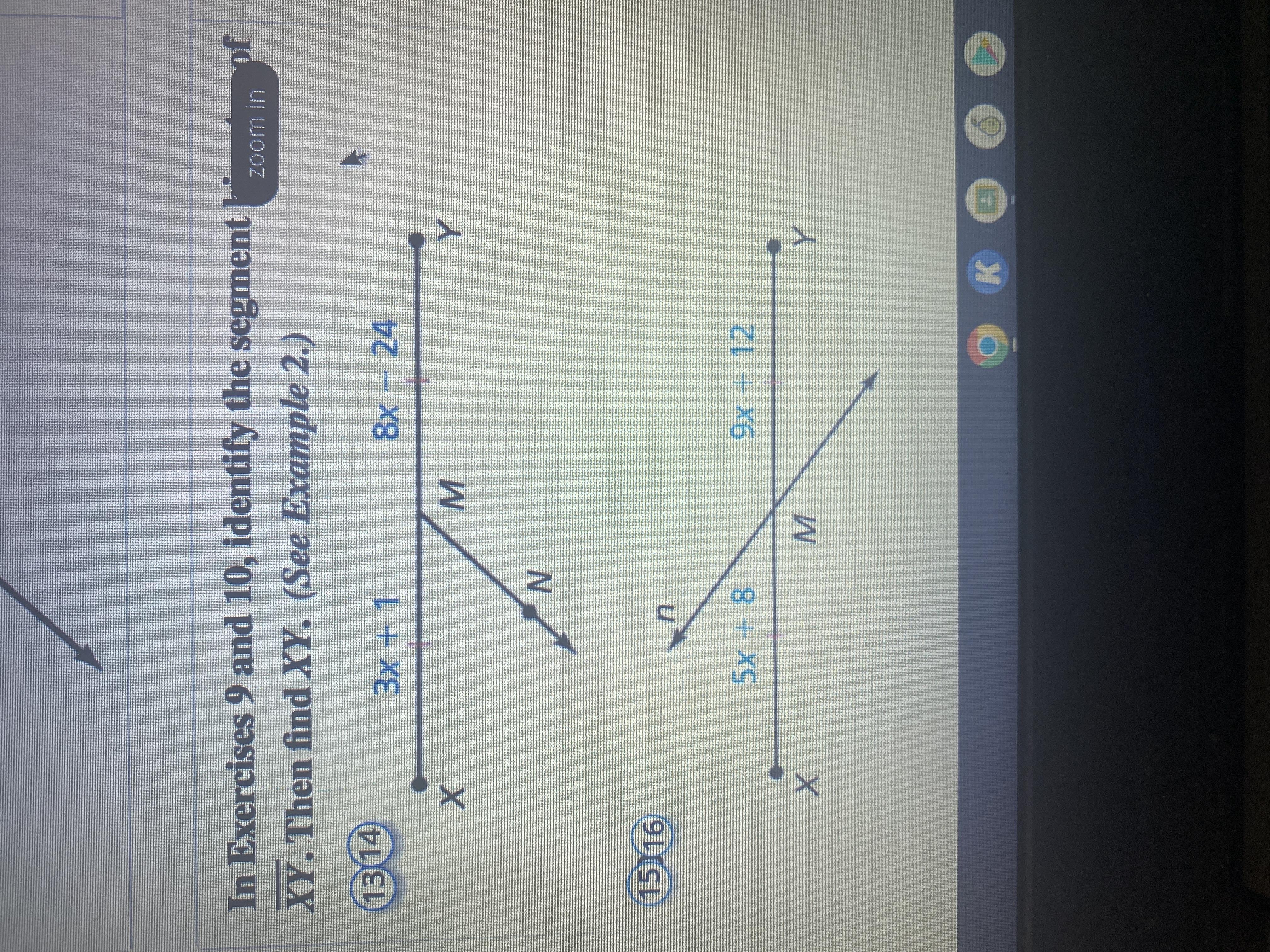
Answers
The length of the line segment XY which was bisected at point M is;
1) 32
2) 6
How to solve division of line segments?
1) From the given line segments, it is clear that XM is congruent to YM since M bisects XY. Thus;
XM = YM and XM + YM = XY
We are given that;
XM = 3x + 1
YM = 8x - 24
Thus;
3x + 1 = 8x - 24
8x - 3x = 1 + 24
5x = 25
x = 25/5
x = 5
Thus;
XM = 3(5) + 1 = 16
YM = 8(5) - 24 = 16
XY = 16 + 16 = 32
2) From the given line segments, it is clear that XM is congruent to YM since M bisects XY. Thus;
XM = YM and XM + YM = XY
We are given that;
XM = 5x + 8
YM = 9x + 12
Thus;
5x + 8 = 9x + 12
9x - 5x = 8 - 12
4x = -4
x = -1
XM = 5(-1) + 8 = 3
YM = 9(-1) + 12 = 3
XY = 6
Read more about division of line segments at; https://brainly.com/question/17374569
#SPJ1
Figure B is a scaled copy of Figure A.
Figure A
14
Figure B
56
16
7
64
28
What is the scale factor from Figure A to Figure B?

Answers
Answer:
4
Step-by-step explanation:
Notice each side was increased by 4 times
You can set up a ratio of
\(\frac{new}{old}\)
then reduce or divide
Marie will earn $15 Per hour at a new job. During training, she will earn $10 per hour.
What percent of Marie's regular hourly rate will she earn during training
Answers
The percent that Marie will earn during her training is 66.67%.
What is percentage?
Percentage is a number or ratio that can be expressed as a fraction of 100. If we have to calculate percent of a number, divide the number by the whole and multiply by 100. Hence, the percentage means, a part per hundred. The word per cent means per 100. It is represented by the symbol “%”.
Given,
She earns working in new job = $15
She earns while training = $10
percentage she will earn during her training
= earing during training/earning during job multiplied by 100.
= 10/15(100)
=66.67%
To know more about percentage, visit:
https://brainly.com/question/13963757
#SPJ13
Help me with this please!!!

Answers
this question answer is 4.25
find the area of the given triangle. round your answer to the nearest tenth. do not round any intermediate computations. 18 62°
Answers
To find the area of the given triangle with a side length of 18 and an angle of 62 degrees, we can use the formula for the area of a triangle: A = 1/2 * base * height.
In this case, the base of the triangle is given as 18, but we need to find the height. To find the height, we can use the trigonometric relationship between the angle and the sides of the triangle. The height is equal to the length of the side opposite the given angle. Using trigonometry, we can determine the height by multiplying the length of the base by the sine of the angle: height = 18 * sin(62°).
Once we have the height, we can calculate the area using the formula: A = 1/2 * base * height. Plugging in the values, we get A = 1/2 * 18 * 18 * sin(62°). Finally, we round the answer to the nearest tenth to obtain the final result.
To learn more about triangle click here :
brainly.com/question/2773823
#SPJ11
A minivan is traveling at 80.5 kilometers per hour. Cargo is strapped to the roof at a height of 1.75 meters. The car hits a concrete barrier, and the cargo is ejected from the roof. Use the following two equations to determine how long it takes for the cargo to hit the ground and how far it travels in the horizontal direction. Let y represent height in meters, x represent horizontal distance in meters, and t represent time in seconds. Equation 1: y = -4.9t2 + 1.75 Equation 2: y = -0.0081x2 + 1.75
Answers
The time taken for the cargo to hit the ground will be 0.6 seconds and it travels in the horizontal direction for around 14.69 feet.
What is equation?The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions. For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, which are separated by the 'equal' sign. The point-slope form, standard form, and slope-intercept form are the three main types of linear equations. The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions. For instance, the equation 3x + 5 = 14 consists of the two equations 3x + 5 and 14, which are separated by the 'equal' sign.
Here,
The calculations are attached in images.
To calculate t we will use that is y because at the moment of cargo will have a height 0, so we get,
= −4.9t² +1.75
-1.75=-4.9t²
t²=-1.75/-4.9
t²=√0.3571
=0.6 seconds
Now we will calculate x, then y = 0
because since the cargo will be on the ground it will no have height, so
0= -0.0081x²+1.75
-1.75 =-0.0081x²
x²=-1.75/-0.0081
x= √216.04 = 14.69 feet
It will take the cargo 0.6 seconds to hit the ground, and it will travel 14.69 feet in a horizontal direction.
To know more about equation,
https://brainly.com/question/649785
#SPJ4


Carter Motor Company claims that its new sedan, the Libra, will average better than 70 miles per gallon in the city. Use μ, the true average mileage of the Libra. Express the null hypothesis H0 and the alternative hypothesis H1 in symbolic form.
Answers
The H0: μ = 70 H1: μ > 70 These are the null and alternative hypotheses in symbolic form for the given scenario.
How we Express the null hypothesis and the alternative hypothesis in symbolic form?express the null hypothesis (H0) and alternative hypothesis (H1) for the given situation involving the Carter Motor Company and their claim about the Libra's average city mileage.
The null hypothesis (H0) is the default assumption that there is no difference or relationship between the tested parameters. In this case, it would be that the true average mileage (μ) of the Libra is equal to 70 miles per gallon in the city:
H0: μ = 70
The alternative hypothesis (H1) is the claim that we want to test, which is that the true average mileage (μ) of the Libra is better than (greater than) 70 miles per gallon in the city:
H1: μ > 70
These are the null and alternative hypotheses in symbolic form for the given scenario.
Learn more about Hypothesis
brainly.com/question/29519577
#SPJ11
a company makes wax candles in the shape of a cylinder. each candle has a diameter of inches and a height of inches. how much wax will the company need to make candles? use for , and do not round your answer.
Answers
The company will need 6π cubic inches of wax to make a single candle.
Given that the company makes wax candles in the shape of a cylinder, each candle has a diameter of 2 inches and a height of 6 inches.
Now, we need to find out how much wax will the company need to make candles.
The formula to find out the volume of a cylinder is given byπr²h,
where r is the radius of the circular base, h is the height of the cylinder and π is the mathematical constant (approx. 3.14159).
Here, Diameter of the cylindrical candle = 2 inchesTherefore, radius (r) of the candle = diameter / 2= 2 / 2= 1 inch
Height (h) of the candle = 6 inchesSubstitute the values of r and h in the formula for the volume of a cylinder and simplify to get,
Volume of the cylindrical candle = πr²h= π(1)²(6)= π(1)(1)(6)= 6π cubic inches
Therefore, the company will need 6π cubic inches of wax to make a single candle.
Know more about cubic inches here:
https://brainly.com/question/11610634
#SPJ11
Which expression is equivalent to 100,000
Answers
Answer:
the answer is 10 with a little 4 on the top right corner
Step-by-step explanation:
count your zeros
Find the following areas. = cos(38).
(a) Find the area inside one loop of r = cos(30).
(b) Find the area inside one loop of r = sin² 0.
(c) Area between the circles r = 2 and r = 4 sin 0,
(d) Area that lies inside r = 3 + 3 sin and outside r = 2.
Answers
(a) The area inside one loop of r = cos(30) is equal to π/3 square units. (b) The area inside one loop of r = sin^2(θ) is equal to π/2 square units. (c) The area between the circles r = 2 and r = 4 sin(θ) is equal to 6π square units. (d) The area that lies inside r = 3 + 3 sin(θ) and outside r = 2 is equal to 9π/2 square units.
(a) To find the area inside one loop of r = cos(30), we need to integrate the function r^2 with respect to θ over one complete revolution. In this case, the limits of integration are 0 to 2π. Evaluating the integral, we get (1/3)π - (-1/3)π = π/3 square units.
(b) To find the area inside one loop of r = sin^2(θ), we follow a similar approach and integrate r^2 with respect to θ over one complete revolution. The limits of integration are again 0 to 2π. Evaluating the integral, we get (1/2)π - 0 = π/2 square units.
(c) To find the area between the circles r = 2 and r = 4 sin(θ), we calculate the area enclosed by the outer circle (r = 4 sin(θ)) and subtract the area enclosed by the inner circle (r = 2). Integrating r^2 with respect to θ over one complete revolution, the area is given by (1/2)∫(16sin^2(θ) - 4) dθ from 0 to 2π. Evaluating the integral, we get 6π square units.
(d) To find the area that lies inside r = 3 + 3 sin(θ) and outside r = 2, we calculate the area enclosed by the outer curve (r = 3 + 3 sin(θ)) and subtract the area enclosed by the inner curve (r = 2). Integrating r^2 with respect to θ over one complete revolution, the area is given by (1/2)∫((3 + 3 sin(θ))^2 - 4) dθ from 0 to 2π. Evaluating the integral, we get 9π/2 square units.
Learn more about integral here:
https://brainly.com/question/31059545
#SPJ11
Can someone please help me

Answers
Answer:
1) D
2) B
3) A
4) D
Step-by-step Explanation:
1) 1,300,000
= 1.3 × 10⁶
2) 0.052
= 5.2 × 10⁻²
3) 4,500
= 4.5 × 10³
4) 0.00061
= 6.1 × 10⁻⁴
Complete the equation of the line through (-6,5) and (-3,3). use exact numbers y=
Answers
We know the line equation is expressed by
y = mx + b, where is m is its slope (how inclinated it is) and b is intercept with the y-axis.
Finding m
We find its inclination, its slope, m, by
\(\begin{gathered} m=\frac{\Delta y}{\Delta x} \\ =\frac{y_2-y_1}{x_2-x_1} \\ \end{gathered}\)Let's say
(x₁, y₁) = (-6, 5)
(x₂, y₂) = (-3, 3)
Then
\(\begin{gathered} m=\frac{3-5}{-3-(-6)} \\ =\frac{-2}{-3+6}=\frac{-2}{3} \\ m=-\frac{2}{3} \end{gathered}\)Then y = -(2/3)x + b,
Finding b
Since b is intercept with the y-axis, we know it intercepts y when x = 0
Using the equation we have found y = -(2/3)x + b, and replacing one point given by the question (x₂, y₂) = (-3, 3)
y = -(2/3)x + b
3 = -(2/3)(-3) + b
3 = -2 + b
3 + 2 = b
Then, b = 5
Therefore,
Answer, y = -(2/3)x + 5,
Suppose P (B) = 0.6, P (A|B) = 0.2, P (A|B′) = 0.3.
(a) Find P (B′).
(b) Explain why B and B′constitute a partition of the sample space S.
(c) Use the Law of Total Probability to find P (A). (d) Use Bayes’ Theorem to find P (B|A).
2. An experiment consists of tossing two dice and recording the score on
each. Consider the events
A: first die is even
B: sum of dice is 4
C: sum of dice is 5
(a) Find P (A), P (B), P (A ∩B), P (A|B), P (B|A).
(b) Are the events A and B independent? Explain your answer.
(c) Are the events A and B mutually exclusive? Explain your answer.
(d) Find P (C), P (A ∩C), P (A|C), P (C|A).
(e) Are the events A and C independent? Explain your answer.
(f) Are the events A and C mutually exclusive? Explain your answer.
Answers
(a) P(A) = 0.24, P(B) = 3/36, P(A ∩ B) = 1/36, P(A|B) = 1/3, P(B|A) = 1/18. (b) Events A and B are not independent, and they are not mutually exclusive (c) P(C) = 4/36, P(A ∩ C) = 2/36, P(A|C) = 1/2, P(C|A) = 1/3. (d) Events A and C are not independent, and they are not mutually exclusive.(e) Events A and C are not independent.(f) Events A and C are not mutually exclusive.
(a) To find P(B'), we can use the complement rule. The complement of event B (denoted as B') is the event that B does not occur. So, P(B') = 1 - P(B) = 1 - 0.6 = 0.4.
(b) Events B and B' constitute a partition of the sample space S because they are mutually exclusive and exhaustive.
- Mutually exclusive: Events B and B' cannot occur simultaneously, meaning if B occurs, B' cannot occur and vice versa.
- Exhaustive: Either B or B' must occur, as they cover all possible outcomes.
(c) We can use the Law of Total Probability to find P(A). The law states that for any event A and a set of mutually exclusive and exhaustive events B1, B2, ..., Bn, the probability of A is the sum of the probabilities of A given each Bi, multiplied by the probability of Bi.
In this case, we have B and B' as our events.
P(A) = P(A|B) * P(B) + P(A|B') * P(B')
= 0.2 * 0.6 + 0.3 * 0.4
= 0.12 + 0.12
= 0.24
Therefore, P(A) = 0.24.
(d) To find P(B|A) using Bayes' Theorem, we can rearrange the formula:
P(B|A) = (P(A|B) * P(B)) / P(A)
We already know P(A|B) = 0.2, P(B) = 0.6, and P(A) = 0.24 (calculated in part c).
P(B|A) = (0.2 * 0.6) / 0.24
= 0.12 / 0.24
= 0.5
Therefore, P(B|A) = 0.5.
2. For the second set of questions:
(a) Given:
A: First die is even
B: Sum of dice is 4
C: Sum of dice is 5
To find the probabilities:
P(A) = 3/6 (there are three even numbers: 2, 4, 6, out of six possible outcomes)
P(B) = 3/36 (out of 36 possible outcomes, there are three ways to get a sum of 4: (1, 3), (2, 2), (3, 1))
P(A ∩ B) = 1/36 (only one way to get both an even number and a sum of 4: (2, 2))
P(A|B) = P(A ∩ B) / P(B) = (1/36) / (3/36) = 1/3
P(B|A) = P(A ∩ B) / P(A) = (1/36) / (3/6) = 1/18
(b) Events A and B are independent if and only if P(A ∩ B) = P(A) * P(B). However, P(A ∩ B) = 1/36 ≠ (3/6) * (3/36) = 1/72. Therefore, events A and B are not independent.
(c) Events A and B are not mutually exclusive since it is possible to roll a sum of 4 with an even first die.
(d) To find the probabilities for event C:
P(C) = 4/36 (out of 36 possible outcomes, there are four ways to get
a sum of 5: (1, 4), (2, 3), (3, 2), (4, 1))
P(A ∩ C) = 2/36 (two ways to get both an even number and a sum of 5: (2, 3), (4, 1))
P(A|C) = P(A ∩ C) / P(C) = (2/36) / (4/36) = 1/2
P(C|A) = P(A ∩ C) / P(A) = (2/36) / (3/6) = 1/3
(e) Events A and C are independent if and only if P(A ∩ C) = P(A) * P(C). However, P(A ∩ C) = 2/36 ≠ (3/6) * (4/36) = 1/9. Therefore, events A and C are not independent.
(f) Events A and C are not mutually exclusive since it is possible to roll a sum of 5 with an even first die.
Learn more about probability here: https://brainly.com/question/32117953
#SPJ11
Here is a frequency distribution table (FDT) for a small data set:
data value frequency
30 18
31 29
32 11
33 23
34 17
Find the following measures of central tendency.
mean (¯xx¯) =Incorrect(Please show your answer to one decimal place.)
median =Incorrect(Please enter an exact answer.)
mode =Incorrect(Please enter an exact answer.)
Answers
The total frequency is even (98), the median is the average of the two middle values, which are 31 and 33. So, the median is (31+33)/2 = 32.
To find the mean, we need to compute the sum of products of data values and their frequencies and divide by the total frequency:
(3018 + 3129 + 3211 + 3323 + 34*17) / (18+29+11+23+17) = 31.1
So, the mean is 31.1.
To find the median, we need to find the middle value of the ordered data set. First, we need to compute the cumulative frequency distribution:
data value frequency cumulative frequency
30 18 18
31 29 47
32 11 58
33 23 81
34 17 98
Since the total frequency is even (98), the median is the average of the two middle values, which are 31 and 33. So, the median is (31+33)/2 = 32.
To find the mode, we need to look for the data value(s) with the highest frequency. In this case, the mode is 31 because it has the highest frequency of 29, which is larger than the frequencies of all other values.
To learn more about total frequency visit:https://brainly.com/question/30358157
#SPJ11
Looking at the top of tower A and base of tower B from points C and D, we find that ∠ACD = 60°, ∠ADC = 75° and ∠ADB = 30°. Let the distance between points C and D be 100. Find the height AB of the tower.
Picture attached for the problem. Please show your work too. Thanks!

Answers
Answer:
\(\text{Exact: }AB=25\sqrt{6},\\\text{Rounded: }AB\approx 61.24\)
Step-by-step explanation:
We can use the Law of Sines to find segment AD, which happens to be a leg of \(\triangle ACD\) and the hypotenuse of \(\triangle ADB\).
The Law of Sines states that the ratio of any angle of a triangle and its opposite side is maintained through the triangle:
\(\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}\)
Since we're given the length of CD, we want to find the measure of the angle opposite to CD, which is \(\angle CAD\). The sum of the interior angles in a triangle is equal to 180 degrees. Thus, we have:
\(\angle CAD+\angle ACD+\angle CDA=180^{\circ},\\\angle CAD+60^{\circ}+75^{\circ}=180^{\circ},\\\angle CAD=180^{\circ}-75^{\circ}-60^{\circ},\\\angle CAD=45^{\circ}\)
Now use this value in the Law of Sines to find AD:
\(\frac{AD}{\sin 60^{\circ}}=\frac{100}{\sin 45^{\circ}},\\\\AD=\sin 60^{\circ}\cdot \frac{100}{\sin 45^{\circ}}\)
Recall that \(\sin 45^{\circ}=\frac{\sqrt{2}}{2}\) and \(\sin 60^{\circ}=\frac{\sqrt{3}}{2}\):
\(AD=\frac{\frac{\sqrt{3}}{2}\cdot 100}{\frac{\sqrt{2}}{2}},\\\\AD=\frac{50\sqrt{3}}{\frac{\sqrt{2}}{2}},\\\\AD=50\sqrt{3}\cdot \frac{2}{\sqrt{2}},\\\\AD=\frac{100\sqrt{3}}{\sqrt{2}}\cdot\frac{ \sqrt{2}}{\sqrt{2}}=\frac{100\sqrt{6}}{2}={50\sqrt{6}}\)
Now that we have the length of AD, we can find the length of AB. The right triangle \(\triangle ADB\) is a 30-60-90 triangle. In all 30-60-90 triangles, the side lengths are in the ratio \(x:x\sqrt{3}:2x\), where \(x\) is the side opposite to the 30 degree angle and \(2x\) is the length of the hypotenuse.
Since AD is the hypotenuse, it must represent \(2x\) in this ratio and since AB is the side opposite to the 30 degree angle, it must represent \(x\) in this ratio (Derive from basic trig for a right triangle and \(\sin 30^{\circ}=\frac{1}{2}\)).
Therefore, AB must be exactly half of AD:
\(AB=\frac{1}{2}AD,\\AB=\frac{1}{2}\cdot 50\sqrt{6},\\AB=\frac{50\sqrt{6}}{2}=\boxed{25\sqrt{6}}\approx 61.24\)
Answer:
\( \displaystyle 25 \sqrt{6} \)
Step-by-step explanation:
the triangle ∆ABD is a special right angle triangle of which we want to figure out length of its shorter leg (AB).
to do so we need to find the length of AD (the hypotenuse). With the help of ∆ADC it can be done. so recall law of sin
\( \boxed{ \displaystyle \frac{ \alpha }{ \sin( \alpha ) } = \frac{ \beta }{ \sin( \beta ) } = \frac{ c}{ \sin( \gamma ) } }\)
we'll ignore B/sinB as our work will be done using the first two
step-1: assign variables:
\( \sin( \gamma ) = \sin( {60}^{ \circ} ) \)\(c=AD\)\( \rm \sin( \alpha ) = \sin( {180}^{ \circ} - ({60}^{ \circ} + {75}^{ \circ} )) = \sin( {45}^{ \circ} ) \)\(a=100\)step-2: substitute
\( \displaystyle \frac{100}{ \sin( {45}^{ \circ} )} = \frac{AD }{ \sin( {60}^{ \circ} )} \)
recall unit circle therefore:
\( \displaystyle \frac{100}{ \dfrac{ \sqrt{2} }{2} } = \frac{AD }{ \dfrac{ \sqrt{3} }{2} } \)
simplify:
\(AD = 50 \sqrt{6} \)
since ∆ABD is a 30-60-90 right angle triangle of which the hypotenuse is twice as much as the shorter leg thus:
\( \displaystyle AB = \frac{50 \sqrt{6} }{2}\)
simplify division:
\( \displaystyle AB = \boxed{25 \sqrt{6} }\)
and we're done!
how many ways are there to arrange the letters in visiting with no pair of consecutive is?
Answers
There are 32,160 ways to arrange the letters in ""visiting"" with no pair of consecutive ""i's"".
To count the number of ways to arrange the letters in ""visiting"" with no pair of consecutive ""i's"", we can use the principle of inclusion-exclusion.
Let's first consider the total number of arrangements of the letters in ""visiting"" without any restrictions. We have 8 letters, so the total number of arrangements is 8! = 40,320.
Now let's consider the number of arrangements where the two ""i's"" are together. We can treat the two ""i's"" as a single letter, so we have 7 letters to arrange. There are 7! = 5,040 ways to arrange these letters, and within each arrangement there are 2! = 2 ways to arrange the ""i's"". So there are 2 x 5,040 = 10,080 arrangements where the two ""i's"" are together.
However, we have overcounted some arrangements, namely those where there are three consecutive ""i's"". To count these arrangements, we can treat the three ""i's"" as a single letter, so we have 6 letters to arrange.
There are 6! = 720 ways to arrange these letters, and within each arrangement there are 3! = 6 ways to arrange the ""i's"".
So there are 6 x 720 = 4,320 arrangements where there are three consecutive ""i's"".
Thus, by the principle of inclusion-exclusion, the number of arrangements of ""visiting"" with no pair of consecutive ""i's"" is:
8! - 10,080 + 4,320 = 32,160
Therefore, there are 32,160 ways to arrange the letters in ""visiting"" with no pair of consecutive ""i's"".
Click the below link, to learn more about consecutive pairs:
https://brainly.com/question/29012599
#SPJ11
Tell whether the angles are complementary or supplementary. Then find the value of x.
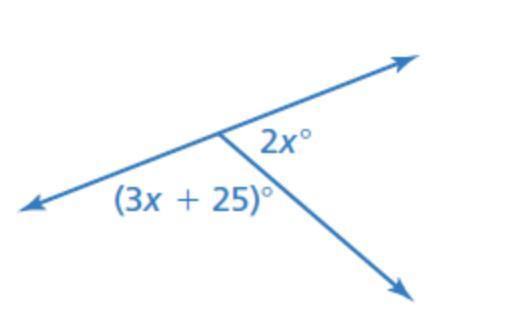
Answers
3x+25+2x=180
5x=155
x=31
Hope this helps!! :)
T/F: Nonsampling errors reduce the overall quality of data regardless of the data collection method.
Answers
True. Nonsampling errors refer to errors that occur during the data collection process that are not related to the sampling method used. These errors can occur in any type of data collection method, whether it be through surveys, experiments, or observational studies.
Nonsampling errors can arise due to a variety of reasons, such as poor survey design, biased sampling methods, inadequate training of surveyors, errors in data entry or processing, or even deliberate fraud.
Nonsampling errors can have a significant impact on the quality of the data collected, as they can introduce biases and inaccuracies into the results. These errors can result in incorrect conclusions and decisions based on the data, which can have serious consequences. Therefore, it is important to take steps to minimize nonsampling errors during the data collection process, such as carefully designing surveys, ensuring proper training of surveyors, and conducting thorough quality checks on the data collected.
Learn more about Nonsampling here:
https://brainly.com/question/15396688
#SPJ11
Helpppppppppppppppppppp

Answers
Answer:
\(( {4}^{3} \div {5}^{ - 2} {)}^{5} \)
Step-by-step explanation:
\( {4}^{15} . {5}^{10} \)
hope this will help you more
have a great day..
Step-by-step explanation:
\(( \frac{4 {}^{3} }{5 {}^{ - 2} } ) {}^{5 } \\ ( \frac{4 {}^{15} }{5 {}^{10} } ) \\ \frac{4 {}^{15} }{5 {}^{10} } \)
Jenna collected data on how many CDs her friends owned and how many hours per week they listened to music. Her data is shown in the table.
CDs Owned
15/15/8/18/11
Hours Listened 7 8 5 10 9
Which scatter plot correctly represents this data?
ОА
Ос.
new
CDS Ow
12 16
CDs Owned
Ов.
OD.
CDs Owned
CDs Owned

Answers
Answer:
im pretty sure it would be d
Step-by-step explanation:
Answer:
It is D
Step-by-step explanation:
got it right on the test
Looking north, two skyscrapers are sighted from the viewing deck of the Empire State Building at 1250 feet up. One skyscraper is sighted at a 20° angle of depression and a second skyscraper is sighted at a 30° angle of depression. How far apart are the two skyscrapers to the nearest foot?
Answers
Answer:
Step-by-step explanation:

The angle of depression is the angle between the line of sight and a vertical line.
The distance between the two skyscrapers is 1269ft
I've added as an attachment, a figure that illustrates the scenario
First, we calculate distance AB using the following tangent ratio
\(\mathbf{\tan(\theta) = \frac{Opposite}{Adjacent}}\)
So, we have:
\(\mathbf{\tan(60) = \frac{AB}{1250}}\)
Make AB the subject
\(\mathbf{AB = 1250 \times \tan(60)}\)
Next, we calculate distance AC using the following tangent ratio
\(\mathbf{\tan(\theta) = \frac{Opposite}{Adjacent}}\)
So, we have:
\(\mathbf{\tan(60+10) = \frac{AB + BC}{1250}}\)
\(\mathbf{\tan(70) = \frac{AB + BC}{1250}}\)
Make AB + BC, the subject
\(\mathbf{AB + BC = 1250 \times \tan(70)}\)
Make BC the subject
\(\mathbf{BC = 1250 \times \tan(70) - AB}\)
Substitute \(\mathbf{AB = 1250 \times \tan(60)}\)
\(\mathbf{BC = 1250 \times \tan(70) - 1250 \times \tan(60)}\)
\(\mathbf{BC = 1269}\)
Hence, the distance between the two skyscrapers is 1269ft
Read more about angles of depression at:
https://brainly.com/question/13697260

Examples of distribution
Answers
Answer:
see below
Step-by-step explanation:
5(2a+2b+2c)
you must distribute the 5 among the values in parenthesis
4(x-3)
you must distribute the 4 among the values in parenthesis
Hope this helps! :)
Determine the equation of the line that passes through (-8,9) and (2,-6)
Express you answer as a fraction in lowest terms.

Answers
The equation of the line that passes through the points (-8, 9) and (2, -6) is y = (-3 / 2)x - 3.Given two points (-8, 9) and (2, -6). We are supposed to find the equation of the line that passes through these two points.
We can find the equation of a line that passes through two given points, using the slope-intercept form of the equation of a line. The slope-intercept form of the equation of a line is given by, y = mx + b,Where m is the slope of the line and b is the y-intercept.To find the slope of the line passing through the given points, we can use the slope formula: m = (y2 - y1) / (x2 - x1).Here, x1 = -8, y1 = 9, x2 = 2 and y2 = -6.
Hence, we can substitute these values to find the slope.m = (-6 - 9) / (2 - (-8))m = (-6 - 9) / (2 + 8)m = -15 / 10m = -3 / 2Hence, the slope of the line passing through the points (-8, 9) and (2, -6) is -3 / 2.
Now, using the point-slope form of the equation of a line, we can find the equation of the line that passes through the point (-8, 9) and has a slope of -3 / 2.
The point-slope form of the equation of a line is given by,y - y1 = m(x - x1)Here, x1 = -8, y1 = 9 and m = -3 / 2.
Hence, we can substitute these values to find the equation of the line.y - 9 = (-3 / 2)(x - (-8))y - 9 = (-3 / 2)(x + 8)y - 9 = (-3 / 2)x - 12y = (-3 / 2)x - 12 + 9y = (-3 / 2)x - 3.
Therefore, the equation of the line that passes through the points (-8, 9) and (2, -6) is y = (-3 / 2)x - 3. Thus, the answer is (-3/2)x - 3.
For more question on equation
https://brainly.com/question/17145398
#SPJ8
2. Amy has a room that is 6 feet by 10 feet. She bought tiles
that are 8 inches by 6 inches. How many tiles will she
need to cover the floor?
Answers
A unit can be used for measurement, and is commonly found in mathematics to describe length, size, etc.
Because we are dealing with different units here, we first would need to know how many inches are in one foot.
1 foot = 12 inches
Now that we know how many inches are in a foot, we can convert the length and width of the room from feet to inches.
6 feet = 72 inches
10 feet = 120 inches
Taking these numbers, we now need to figure out the area of the floor.
72 × 120 = 8640
Now, find the area of each tile.
6 × 8 = 48
Taking 8640, we can now divide that by 48 to get the number of tiles needed.
8640 ÷ 48 = 180
Therefore, 180 tiles are needed to cover the floor.
Consider a male restroom design with minimum plumbing requirements of 12 water closets and 13 lavatories, which one of the following is closest to the minimum space required with considering urinal substitution? Select one: O a. 222 b. 219 c. 237 d. 249
Answers
none of the provided options (a, b, c, d) appear to be accurate or close to the minimum space required.
To determine the minimum space required for a male restroom design with the given plumbing requirements, we need to consider the minimum space required for water closets and lavatories.
The minimum space required for water closets is typically around 30-36 inches per unit, and for lavatories, it is around 24-30 inches per unit.
Since the design requires a minimum of 12 water closets and 13 lavatories, we can estimate the minimum space required as follows:
Minimum space required for water closets = 12 water closets * 30 inches = 360 inches
Minimum space required for lavatories = 13 lavatories * 24 inches = 312 inches
Adding these two values together, we get a total minimum space requirement of 672 inches.
Among the given options, the closest value to 672 inches is option d) 249. However, this value seems significantly lower than the expected minimum space requirement.
To know more about minimum visit:
brainly.com/question/21426575
#SPJ11
Which of the following is an incorrect description for the number -11/3 A. Negative number B. Rational number C. Repeating decimal D. Terminating decimal
Answers
Answer:
D
Step-by-step explanation:
because -11/3 is a repeating decimal. Terminating decimals are decimals that come to an end.
according to a gallup poll, it is reported that 81% of americans donated money to charitable organizations in 2021. if a researcher were to take a random sample of 6 americans, what is the probability that: a. exactly 5 of them donated money to a charitable cause?
Answers
The probability that exactly 5 out of 6 randomly selected Americans donated money to a charitable cause in 2021 is approximately 0.3931, or 39.31%.
The probability of a single American donating money to a charitable organization in 2021 is given as 81%. Therefore, the probability of an individual not donating is 1 - 0.81 = 0.19.
To calculate the probability of exactly 5 out of 6 Americans donating, we can use the binomial probability formula:
P(X = k) = (n C k) * p^k * (1 - p)^(n - k)
Where:
P(X = k) represents the probability of exactly k successes (donations).
(n C k) is the binomial coefficient, which represents the number of ways to choose k successes from n trials.
p is the probability of success (donation) in a single trial.
(1 - p) represents the probability of failure (not donating) in a single trial.
n is the total number of trials (sample size).
In this case, n = 6, k = 5, p = 0.81, and (1 - p) = 0.19.
Plugging in these values, we can calculate the probability:
P(X = 5) = (6 C 5) * (0.81)^5 * (0.19)^(6 - 5)
P(X = 5) = 6 * (0.81)^5 * (0.19)^1
P(X = 5) = 0.3931
Therefore, the probability that exactly 5 out of 6 randomly selected Americans donated money to a charitable cause in 2021 is approximately 0.3931, or 39.31%.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
-7 + (-9) - (-11) -2

Answers
a 3-digit pin number is selected. what it the probability that there are no repeated digits? the probability that no numbers are repeated is
Answers
The probability that no numbers are repeated = \(\frac{720}{1000}=0.72\)
The probability that there are no repeated digits in a 3-digit pin number is 0.72.
Formula used:
\(P(n,r)=\frac{n!}{(n-r)!}\\ Probability=\frac{Number of favourable outcomes}{Total number of events in the samples pace}\)
There are 10 digits (0,1,2,3,4,5,6,7,8,9) to choose from.
Therefore, the total number of possible 3-digit pin numbers with no repeated digits is
\(P(10,3)=\frac{10!}{(10-3)!}\\P(10,3)= \frac{10!}{7!}\\P(10,3)=720\)
The total number of possible 3-digit pin numbers \(= 10 * 10 * 10 = 1000\).
Thus, the probability that no numbers are repeated = \(\frac{720}{1000}=0.72\)
Therefore, the probability that there are no repeated digits in a 3-digit pin number is 0.72.
Learn more about probability below
https://brainly.com/question/13604758
what can identifying a correlation do for your research? guide the design of grids or decision matrices. present possible solutions to be explored. aid in the calculation of the mean and mode.
Answers
Identifying Correlation helps in presenting solutions to be explored.
What is Correlation?
Correlation is a statistical metric (a number) that represents the magnitude and direction of a link between two or more variables. A correlation between variables, on the other hand, does not imply that a change in one variable is the cause of a change in the values of the other variable.
Solution:
Identifying Correlation helps in presenting solutions to be explored.
To learn more about Correlation from the given link
https://brainly.com/question/4219149
#SPJ4