John had to pay a combined electric and gas bill $150. The electric portion of the bill was $90. What is the ratio of money spent on electric to that on gas?
Answers
Given:
John had to pay a combined electric and gas bill $150.
The electric portion of the bill was $90.
To find:
The ratio of money spent on electric to that on gas.
Solution:
Let x be the amount of gas bill.
The electric portion of the bill was $90 and John had to pay a combined electric and gas bill $150. So,
\(90+x=150\)
\(x=150-90\)
\(x=60\)
The gas portion of the bill was $60.
The ratio of money spent on electric to that on gas is:
\(\text{Required Ratio}=\dfrac{\text{Electric bill}}{\text{Gas bill}}\)
\(\text{Required Ratio}=\dfrac{90}{60}\)
\(\text{Required Ratio}=\dfrac{3}{2}\)
\(\text{Required Ratio}=3:2\)
Therefore, the ratio of money spent on electric to that on gas is 3:2.
Related Questions
Use the information to answer the following question.
Carolyn was asked to solve the following system of equations.
Her work is shown.
Step 1: 3x – 2y = 7
Step 2: 3x – 2(x + 2) = 7
Step 3: 3x – 2x + 4 = 7
Step 4: x + 4 = 7
Step 5: x = 3
Step 6: y = x + 2
Step 7: y = 3 + 2
Step 8: y = 5
Solution: (3, 5)
Did Carolyn make an error in her work?
Yes, Carolyn did not correctly combine like terms in Step 2.
Yes, Carolyn should have substituted the x-value into the first equation in Step 6.
No, Carolyn solved the system of equations correctly.
Yes, Carolyn did not correctly distribute the negative in Step 3.
Answers
Carolyn made an error in her work because she did not correctly distribute the negative in Step 3.
System of EquationsA system of equations is the given term math for two or more equations with the same variables. The solution of these equations represents the point of the intersection.
You can solve a system of equations by the adding or substitution methods. In the addition method, you eliminate a variable, on the other hand, in the substitution method you replace a variable for the other.
The question gives:3x-2y=7 (1)y=x+2The question shows that Carolyn applies the substitution method because she replaces the variable y (equation 2) in equation 1. See the given step 2.
3x – 2y = 7
3x – 2(x + 2) = 7
3x – 2x - 4 = 7 - here it is the mistake. (Carolyn did not correctly distribute the negative).
Read more about solving systems equations here:
brainly.com/question/12691830
#SPJ1
ed drives to work at a constant speed s. one day he is halfway to work when he immediately turns around, speeds up b8 mph, and drives home. as soon as he is home, he turns and drives to work at6 mph faster than he drove home. his total driving time is exactly 67% greater than usual. find s in mph and write the answer in the corresponding blank on the answer sheet
Answers
The speed s of Ed's drive to work is 24 mph.
Let d be the distance between Ed's home and work, and let t be the time it takes him to drive to work at speed s. Then, we know that Ed drove half the distance to work before turning around, so he drove d/2 miles.
When he turns around, he increases his speed by 8 mph, so his new speed is s+8 mph. He then drives back to his home, covering the same distance of d/2 miles at an increased speed.
The time it takes him to drive home is therefore (d/2)/(s+8) hours. When he arrives home, he turns around and drives to work at a speed of (s+6) mph. The time it takes him to drive to work is then d/(s+6) hours.
Since Ed's total driving time is 67% greater than usual, we know that his new driving time is 1.67t. Setting up an equation using these values, we get:
d/(s+6) + d/2/(s+8) + d/(s) = 1.67t
Simplifying this equation yields:
d = 6t(s+6)/(7s+24)
We also know that Ed drove half the distance to before turning around, so:
d/2 = st/2
Substituting for d and solving for s yields:
s = 24 mph
To know more about distance, refer here:
https://brainly.com/question/23366355#
#SPJ11
Please answer correctly and write explanation

Answers
Answer:
the 3rd choice, 10x + 5, looks good
Step-by-step explanation:
a coefficient is the number in front of a variable , so that's 10
a constant is a number w/o a variable ... so that's 5
I believe that the answer is 10x + 5.
Coefficents are also know as "multipliers". They pair with variables (in this case, that is x). Constants are simply numbers on their own.
Hope that makes sense.
Jose brought 9 pounds of rice for $4. How many pounds of rice did he get per dollar?
Answers
Answer:
1.5 pound ever dollar
Step-by-step explanation:
just calculate
Answer:
2.25 answer
Step-by-step explanation:
9÷4=2.25answer thanks
The CEO has left the company, so the stock prices have changed. The price has changed from $120 per share to $90 per share.
Answers
Answer:
120-90
=30
the change in stock price is $30 per share
Please help I’m stuck!!
When do you have to split up the middle
term in a trinomial when factoring?
Answers
You typically split up the middle term if your a-value (the coefficient on x^2) is not 1.
For example, I'd split up the middle term on 3x^2 + 4x – 4,
but not on x^2 + 4x - 12.
Technically you could on that second one, but you're making a lot of extra and unecessary work for yourself.
Does that make sense?
3 - h divided by 3/4; h=2/3
50 Points!
URGENT!

Answers
Answer:
19/9
Step-by-step explanation:
Important concepts and formulas used to solve the following question:
PEMDAS (Parenthesis, Exponents, Multiplication and Division(Going left to right), Addition and Subtraction(Going left to right). This tells us the order we perform the operations when evaluating an expression. Keep , Change , Flip : Rather than trying to divide a fraction by another fraction, we can use keep change flip which allows us to multiply the fractions rather than dividing them. To do so, we Keep the first fraction, Change the sign to multiplication and Flip the second fraction.Answering the question
We want to evaluate the following expression given that h = 2/3
3 - h ÷ 3/4
==> plug in h = 2/3
3 - 2/3 ÷ 3/4
==> First we do the division before the subtraction according to PEMDAS. Rather than trying to divide a fraction by another fraction we can use "keep change flip" (dividing a number by a fraction is the same as multiplying the number by the fractions reciprocal)
3 - 2/3 × 4/3
==> multiply 2/3 and 4/3
3 - 8/9
==> simplify
19/9
Learn more about evaluating expressions here : https://brainly.com/question/24694393
Learn more about PEMDAS here : https://brainly.com/question/11961214
\(\huge\text{Hey there!}\)
\(\mathsf{3 - h \div \dfrac{3}{4}}\)
\(\mathsf{= \dfrac{3}{1}- \dfrac{2}{3} \div \dfrac{3}{4}}\)
\(\mathsf{= \dfrac{3}{1}- \dfrac{2}{3}\times\dfrac{4}{3}}\)
\(\mathsf{= \dfrac{3}{1} - \dfrac{2\times4}{3\times3}}\)
\(\mathsf{= \dfrac{3}{1} - \dfrac{8}{9}}\)
\(\mathsf{= \dfrac{3\times 9}{1\times9} - \dfrac{8}{9}}\)
\(\mathsf{= \dfrac{27}{9} - \dfrac{8}{9}}\)
\(\mathsf{= \dfrac{27 - 8}{9 - 0}}\)
\(\mathsf{= \dfrac{19}{9}\rightarrow 2 \dfrac{1}{9}}\)
\(\huge\text{Therefore your answer should be:}\)
\(\huge\boxed{\mathsf{\dfrac{19}{9}\ or \ 2\dfrac{1}{9}}}\huge\checkmark\)
\(\uparrow\large\text{Either of those should work because they are practically the same}\\\large\text{thing}\)
\(\huge\text{Good luck on your assignment \& enjoy your day!}\)
~\(\frak{Amphitrite1040:)}\)
You are studying a population of mountain bighorn sheep. There are currently 170 individuals and the intrinsic growth rate is 0.2 per year. Assuming exponential growth, approximately what will the population size be in 4 years
Answers
The population size of mountain bighorn sheep after four years will be approximately 374 individuals.
The intrinsic growth rate of a population is the highest possible growth rate without any environmental or other constraints. Exponential growth is a growth pattern that arises when a population increases in size by a set percentage each year. Exponential growth is one method of modeling population growth and is defined by an accelerating growth rate over time.
The mountain bighorn sheep has an intrinsic growth rate of 0.2 per year, and the formula used to estimate the population size after a given number of years is P = P0ert. In this equation, P0 is the initial population size, P is the final population size, e is Euler's number, r is the intrinsic growth rate, and t is the time in years.
Therefore, to calculate the population size of mountain bighorn sheep after four years, we can use the equation as follows: P = P0ert. By substituting the values given in the problem into the equation, we obtain P = 170 x e^(0.2 x 4). Simplifying the equation yields P = 170 x e^0.8, and rounding this number yields P ≈ 373.96.
Hence, the population size of mountain bighorn sheep after four years will be approximately 374 individuals.
Know more about Exponential growth here:
https://brainly.com/question/1596693
#SPJ11
Colin earned $66.00 raking leaves. If he worked 2.5 today and 3 hours yesterday, how much did he earn per hour?
Answers
66/5.5=12
$12.00/hour
a market research firm conducts telephone surveys with a historical response rate. what is the probability that in a new sample of telephone numbers, at least individuals will cooperate and respond to the questions? in other words, what is the probability that the sample proportion will be at least ? calculate the probability to decimals
Answers
The probability that the sample proportion will be at least 0.375 = 0.8461
Here, te market research firm conducts telephone surveys with a 40% historical response rate.
so, p = 0.4
here, the sample of 400 telephone numbers is n = 400
and \(\hat{p}=0.375\)
The standard deviation would be,
\(\sigma=\sqrt{\frac{p(1-p)}{n} } \\\\\sigma=\sqrt{\frac{0.4(1-0.4)}{400} } \\\\\sigma=0.0245\)
Now we calculate z score :
\(z=\frac{0.375-0.4}{0.0245} \\\\z=-1.0204\)
The probability that the sample proportion will be at least 0.375:
P(\(\hat{p}\) ≥ 0.375)
= P(z > -1.0204)
= 0.8461
Therefore, the required probability is: 0.8461
Learn more about the probability here:
https://brainly.com/question/15124899
#SPJ4
The complete question is;
A market research firm conducts telephone surveys with a 40% historical response rate. What is the probability that in a new sample of 400 telephone numbers, at least 150 individuals will cooperate and respond to the questions? In other words, what is the probability that the sample proportion will be at least 150/400 = .375?
Calculate the probability to 4 decimals.
Use synthetic division and the remainder Theorem to find the indicated function value.
f(x) = 5x³-13x² + 4x-2: f(2)
Answers
To find f(2) using synthetic division, we set up the synthetic division table with the coefficients of the polynomial:
What is synthetic division?Synthetic division is a shorthand method of dividing a polynomial by a linear factor of the form (x - a), where a is a constant. The method is used to simplify the long division process and is particularly useful for finding the roots of a polynomial.The basic idea behind synthetic division is to use the coefficients of the polynomial and the constant a to create a condensed division table that eliminates the need for writing out all the intermediate steps of the division process.2 │ 5 -13 4 -2
│ 10 -6 -2
└───────────
5 -3 -2 0
The last entry in the bottom row of the table gives the remainder of the division, which is f(2). Therefore, we have:
f(2) = 5(2)³ - 13(2)² + 4(2) - 2 = 40 - 52 + 8 - 2 = -6
So, the value of the function f(x) = 5x³-13x² + 4x-2 at x = 2 is f(2) = -6.
To know more about synthetic division , check out :
https://brainly.com/question/24662212
#SPJ1
uppose that the proportion of defective items in a large lot is 10 percent. what is the smallest random sample of items that must be taken from the lot in order for the probability to be at least 99 percent that the proportion of defective items in the sample is less than 13 percent?
Answers
Using Central Limit Theorem,
the smallest possible value of sample size , n is 452...
let Xi = 1 if item is defective or
Xi = 0 if item is not defective
Now, Xn- hat = 1/n ∑Xᵢ= sample proportion for defective items
we have to calculate smallest value of n we require P( Xn- hat <0.13 ) > 0.99
we have,. E(Xᵢ) = μ = 0.1 and variance (Xᵢ)
= (.1 ) (1 - 0.1) =( 0.1) (0.9) = σ²
Since, Xi are Bernoulli random variables
According to limit theorem ,
Z = (Xₙ- hat - u) √n/ sd ~ N(1;0) approximately when n is large
Therefore,
P ( Xₙ -hat < 0.13)
=> P (( Xₙ-hat - u)√n / sd < (0.13 - 0.1 )√n/ √0.09 )
=> P( Z < 0.03 √n/0.03 ) where Z~N(1;0)
=> P( Z< √n/10)
i.e f( √n/10 > f(2.32 ) = 0.99
=> n/ 100 > (2.32)²
=> n = (2.32)²× 100
=> n > 541.02 ~ 542
Thus, smallest possible value is 542..
To learn more about Center limit theorem, refer:
https://brainly.com/question/14099217
#SPJ4
Use matrices A and B. Compute B - A, if you can. (1 point)

Answers
If a city population of 10,000 experiences 100 births, 40 deaths, 10 immigrants, and 30 emigrants in the course of a year, what is its net annual percentage growth rate?0.4%0.8%1.0%4.0%8.0%
Answers
The net annual percentage growth rate of the city population is 0.4%
To calculate the net annual percentage growth rate of a population, we can use the following formula:
Net Annual Percentage Growth Rate = ((Births + Immigrants) - (Deaths + Emigrants)) / Initial Population x 100%
Plugging in the given values, we get:
Net Annual Percentage Growth Rate =\(((100 + 10) - (40 + 30)) / 10,000 x 100%\)
Net Annual Percentage Growth Rate = \((40 / 10,000) x 100%\)
Net Annual Percentage Growth Rate =\(0.4%\)
The net annual percentage growth rate of the city population is 0.4%
for such more questions on growth rate
https://brainly.com/question/25630111
#SPJ11
What is the length of the diagonal from P to Q?

Answers
Answer:
The length of the diagonal from P to Q is
\( \sqrt{ {9}^{2} + {12}^{2} + {8}^{2} } = \sqrt{289} = 17\)
If f(x) = 2x + 3, what is f(-2)?
Answers
Answer:
7
Step-by-step explanation:
Answer:
no answer
Step-by-step explanation:
2(-2)+3=-2
simplify
-4+3=-2
simplify
-1=-2
No answer
If there's something along the lines of no answer and it's multiple choice click that.
Mark can make 42 birthday cakes in 7 days. How many cakes can he make in 5 days?
Answers
Answer:
30
Step-by-step explanation:
if he can make 42 cakes = 7days
therefore x cakes. =5days
you do cross multiplication
i.e. 42x5/7 =30 days
please help
( GIVING BRAINLIEST)

Answers
Answer:
I belive that the solution is 2 gallons and 4 cups
Answer:
1c = 0.0625
36x0.0625=2.25 galon = 2 gal 4 cups
Step-by-step explanation:
Resolve ax/a+x into an infinite series. Write the first 5 terms. Consider x as the variable. Then, use summation notation to create a formula for the infinite series
Answers
The infinite series ax/a+x can be written in the form of a summation notation as \(Σ ( (−1)^n * (x^(n+1))/(a^(n+1)))\), which can be used to calculate the sum of the series for any value of x and a.
The infinite series representing ax/a+x can be written as:
\(∑n=0∞(−1)nx^n+1a^n+1\)
The first 5 terms of this series can be calculated as follows:
\(Term 1 = (x/(a+x))Term 2 = -(x^2/a^2+2ax+x^2) 4Term 3 = (x^3/a^3+3a^2x+3ax^2+x^3) Term 4 = -(x^4/a^4+4a^3x+6a^2x^2+4ax^3+x^4)Term 5 = (x^5/a^5+5a^4x+10a^3x^2+10a^2x^3+5ax^4+x^5)\)
The general formula for the infinite series can be written as:
\(∑n=0∞(−1)nx^n+1a^n+1 = (x/(a+x)) - (x^2/a^2+2ax+x^2) + (x^3/a^3+3a^2x+3ax^2+x^3) - (x^4/a^4+4a^3x+6a^2x^2+4ax^3+x^4) + (x^5/a^5+5a^4x+10a^3x^2+10a^2x^3+5ax^4+x^5) + ...\)
The summation notation for this series can be written as:
\(∑n=0∞(−1)nx^n+1a^n+1 = Σ ( (−1)^n * (x^(n+1))/(a^(n+1)))\)
This formula can be used to calculate the sum of the infinite series for any value of x and a.
The infinite series ax/a+x can be written in the form of a summation notation as \(Σ ( (−1)^n * (x^(n+1))/(a^(n+1)))\), which can be used to calculate the sum of the series for any value of x and a.
Learn more about infinite series here:
https://brainly.com/question/29062598
#SPJ4
Write an equation of the line through (-3,- 6) having slope17/16Give the answer in standard form.The equation of the line is
Answers
The equation of a line in Standard form is:
\(Ax+By=C\)Where "A", "B" and "C" are Integers ("A" is positive).
The Slope-Intercept form of the equation of a line is:
\(y=mx+b\)Where "m" is the slope and "b" is the y-intercept.
In this case you know that:
\(m=\frac{17}{16}\)And knowing that the line passes through the point
\(\mleft(-3,-6\mright)\)You can substitute values and solve for "b":
\(\begin{gathered} y=mx+b \\ -6=(\frac{17}{16})(-3)+b \\ \\ \\ -6=-\frac{51}{16}+b \\ \\ -6=-\frac{51}{16}+b \\ \\ -6+\frac{51}{16}=b \\ \\ b=-\frac{45}{16} \end{gathered}\)Then, the equation of this line in Slope-Intercept form is:
\(y=\frac{17}{16}x-\frac{45}{16}\)Now that you have this equation, you can write it in Standard form as following:
\(\begin{gathered} y+\frac{45}{16}=\frac{17}{16}x \\ \\ \frac{45}{16}=\frac{17}{16}x-y \\ \\ \frac{17}{16}x-y=\frac{45}{16} \end{gathered}\)The answer is:
\(\frac{17}{16}x-y=\frac{45}{16}\)true or false? "Because in a randomized controlled trial (RCT), the assignment is random, therefore there is no coverage bias---by definition" g
Answers
The statement "Because in a randomized controlled trial (RCT), the assignment is random, therefore there is no coverage bias---by definition" g is false because, it is important to consider both randomization and other factors when assessing the potential for bias in an RCT.
Random assignment in an RCT can help to reduce selection bias, but it does not guarantee the absence of coverage bias.
Coverage bias can occur if the participants who are enrolled in the trial do not represent the population to which the results will be generalized.
For example, if the trial only includes participants who are healthier or more compliant than the typical patient, the results may not be applicable to the broader population.
Therefore, it is important to consider both randomization and other factors when assessing the potential for bias in an RCT.
for such more question on RCT
https://brainly.com/question/23819325
#SPJ11
What is the completely factored form of f(x) = x3 – 2x2 – 5x 6? f(x) = (x 2)(x – 3)(x 6) f(x) = (x 2)(x – 3)(x – 6) f(x) = (x – 2)(x 3)(x – 1) f(x) = (x 2)(x – 3)(x – 1)
Answers
\(x^3-2x^2-5x +6\\\\=x^3-x^2-x^2+x-6x+6\\\\=x^2(x-1)-x(x-1)-6(x-1)\\\\=(x-1)(x^2 -x -6)\\\\=(x-1)(x^2 -3x +2x -6)\\\\=(x-1)\textbf{[} x(x-3) +2(x-3)\textbf{]}\\\\=(x-1)(x-3)(x+2)\)
The requried, factored form of the given expression is (x - 1)(x - 3)(x + 2).
What are the factors?A number or algebraic expression that evenly divides another number or expression—i.e., leaves no remainder—is referred to as a factor.
To factor the polynomial f(x) = x³ – 2x² – 5x + 6 completely, we can use a combination of the rational root theorem and synthetic division.
We can use synthetic division to test each possible root and see if it is a factor of the polynomial. Starting with x = 2, we have:
2 | 1 -2 -5 6
| 2 0 -10
|_____________
1 0 -5 -4
Since the remainder is not zero, x = 2 is not a factor of the polynomial. Continuing with the other possible roots, we find that x = 1 and x = 3 are roots, but x = -1, x = -2, x = -3, and x = -6 are not roots.
Therefore, we can factor the polynomial as follows:
f(x) = x² – 2x² – 5x + 6
= (x - 1)(x - 3)(x + 2)
So the completely factored form of f(x) is f(x) = (x - 1)(x - 3)(x + 2).
Learn more about Factors here:
https://brainly.com/question/24182713
#SPJ7
0.60792 liters x ________ = 607.92 mL
Answers
0.60792 liters x 1000 = 607.92 mL
Multiplying the volume in liters by 1000 converts it to milliliters.
Helppppp plssss I need answer fast will give brainlest answer

Answers
Answer:
A. Undefined
Step-by-step explanation:
Any vertical lines' slope is undefined.
Answer:
A. Undefined
Step-by-step explanation:
Because the line is vertical.
To find the surface area of a triangular prism, use the formulaS= 2B + Ph where B is the area of the base, P is the perimeter of thebases, and h is the height of the prism.The height of the prism is_____ftThe area of the base is_____ftThe perimeter of the base is_____ftFill in the formula. S= 2.____+____X_____The surface area of the triangular prism is_____ft

Answers
ANSWER :
The height of the prism is h = 7 ft
The are of the base is B = 12 ft^2
The perimeter of the base is P = 18 ft
Fill in the formula. S = 2x12 + 18x7
The surface area of the triangular prism is 150 ft^2
EXPLANATION :
The given formula for the surface area is :
\(S=2B+Ph\)where B = Base area
P = perimeter of the bases
h = height of the prism
The height of the prism is h = 7 ft
The base is a triangle with dimensions of b = 8 ft and a height h = 3 ft
The area of a triangle is :
\(\begin{gathered} A=\frac{1}{2}bh \\ \\ A=\frac{1}{2}(8)(3) \\ \\ A=12ft^2 \end{gathered}\)The are of the base is B = 12 ft^2
The perimeter of the base is 5 + 5 + 8 = 18 ft, so P = 18 ft
Substitute the results in the formula :
\(\begin{gathered} S=2B+Ph \\ S=2(12)+18(7) \\ S=150ft^2 \end{gathered}\)A researcher wanted to estimate the mean number of hours adults spend formally exercising each week. She gathered a random sample and created a 95% confidence interval of (0.45 hours, 7.94 hours). Which of the following is the correct interpretation of this confidence interval?
Select one: O a. Weare 95% confident that the population mean number of hours adults spend on formal exercise each week lies between 0.45 and 7.94.
O b. There is a 0.95 probability that adults exercise formally between 0.45 hours and 7.94 hours per week.
O c. The sample mean number of hours adults spend on formal exercise each week lies between 0.45 and 7.94.
O d. The population mean number of hours adults spend on formal exercise each week lies between 0.45 and 7.94.
O e. We are 95% confident that the sample mean number of hours adults spend on formal exercise each week lies between 0.45 and 7.94.
Answers
The correct interpretation of the given confidence interval is: “We are 95% confident that the population mean number of hours adults spend on formal exercise each week lies between 0.45 and 7.94.”
Option (a) is the correct interpretation because a confidence interval provides an estimate of the range within which the true population parameter (in this case, the mean number of hours spent on formal exercise) is likely to fall. The confidence level of 95% indicates that if we were to repeat the sampling process and construct confidence intervals, 95% of those intervals would contain the true population mean.
Therefore, we can say with 95% confidence that the population mean lies within the interval (0.45 hours, 7.94 hours). Option (b) is incorrect because probabilities are not associated with confidence intervals. Options (c) and € refer to the sample mean, not the population mean. Option (d) incorrectly suggests that we know the true population mean is within the interval, whereas the confidence interval provides an estimate of the likely range.
Learn more about Population mean here: brainly.com/question/33543874
#SPJ11
calculator for equation a car left the house traveling north at 10 a.m. another car left the house traveling south two hours later. if the cars traveled at the same rate and were 550 miles apart at 4 p.m., what was the rate of each car ?
Answers
The rate of each car is 55 miles per hour.
In order to find the rate of each car, we need to follow the given steps :
1. Let's denote the rate of each car as R (in miles per hour).
2. The first car traveled north from 10 a.m. to 4 p.m., which is 6 hours. So, the distance covered by the first car can be represented as 6R.
3. T he second car traveled south from 12 p.m. to 4 p.m., which is 4 hours. So, the distance covered by the second car can be represented as 4R.
4. According to the problem, the total distance between the two cars at 4 p.m. is 550 miles. Therefore, the sum of the distances covered by both cars should equal 550 miles.
5. Now, we can set up an equation: 6R + 4R = 550
6. Combine the terms: 10R = 550
7. Solve for R: R = 550 / 10 = 55
So, the rate of each car was 55 miles per hour.
To learn more about equations visit : https://brainly.com/question/2972832
#SPJ11
Find the third side in simplest radical form

Answers
Answer:
x= 2\(\sqrt{6}\)
Step-by-step explanation:
To solve this problem we first observe the Pythagoras equation. If a=x and b = 7 are the lengths of the legs of a right triangle and c= \(\sqrt{73}\) is the length of the hypotenuse, then the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.
This relationship is represented by the formula:
a*a + b*b = c*c
\(x^{2}\) + \(7^{2}\) = \((\sqrt{73} )^2\)
=> x= \(2\sqrt{6}\)
Brent is skiing down a mountain. If his altitude
changes by -15 feet per second, what will be his
!
Answers
Answer:
-900
Step-by-step explanation:
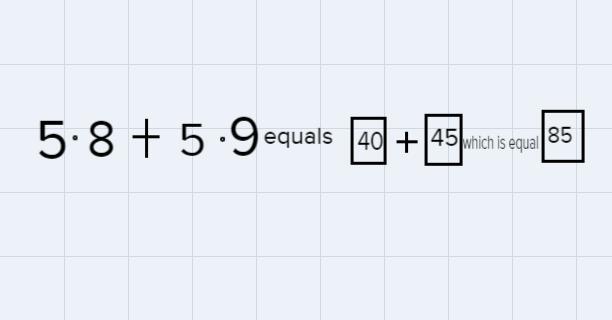
Answer the questions below about Line 1 and Line 2 shown below.5. (8 + 9)Line 15. 8 + 5.9Line 2The expression was rewritten using the5. (8 + 9) equals 5.which equals5 - 8 + 5 · 9 equalswhich equals

Answers
Given the expressions
\(\begin{gathered} 5\cdot(8+9)---------\text{ line 1} \\ 5\cdot8+5\cdot9--------\text{ line 2} \end{gathered}\)The expresion was rewritten using the Distributive property