Initially 100 milligrams of a radioactive substance was present. After 6 hours the mass had decreased by 3%. If the rate of decay is proportional to the amount of the substance present at time t, determine the half-life of the radioactive substance. (Round your answer to one decimal place.)
Answers
The radioactive compound has a half-life of around 3.09 hours.
The period of time needed for a radioactive substance's initial quantity to decay by half is known as its half-life. The half-life of a drug may be calculated as follows if the rate of decay is proportionate to the amount of the substance existing at time t:
Let t be the half-life of the substance, then after t hours, the amount of the substance present will be,
100 mg × \(\dfrac{1}{2}\) = 50 mg.
At time 6 hours, the amount of the substance present is,
100 mg × (1 - 3%) = 97 mg.
Given that the amount of material available determines how quickly something degrades,
The half-life can be calculated as follows:
\(t = 6 \times \dfrac{50}{ 97} = 3.09 \ hours\)
Therefore, the half-life of the radioactive substance is approximately 3.09 hours.
Learn more about half-life:
brainly.com/question/24710827
#SPJ12
Related Questions
helpppp plzzz plz plzz
Apples are on sale at the local fruit stand at 4 lbs. for $2.60. Which equation can be used to find the cost, c, of n pounds of apples?
c = 4
c = 8n
c = .65n
c = 2.60n
Answers
Precalculus question:
A polynomial f(x) and one or more of its zeros are given. (pictured below)
a) Find all the zeros. Write in the exact simplest form.
b) Factor f(x) as a product of linear factors
c) Solve the equation f(x)=0

Answers
Considering the polynomial f(x) = x^4 - 16x³ + 70x² + 48x - 219, we have that:
a) The zeros are: x = -1.995, x = 1.995, x = 8 - 3i, x = 8 + 3i.
b) The linear factors are: (x + 1.995)(x - 1.995)(x - 8 + 3i)(x - 8 - 3i).
c) The solutions to f(x) = 0 are: x = -1.995, x = 1.995, x = 8 - 3i, x = 8 + 3i.
How to obtain the zeros of the polynomial?The given zero of the polynomial is:
8 + 3i
Hence it's conjugate is also a zero, that is:
8 - 3i.
Thus the first two factors are given as follows:
(x - 8 - 3i)(x - 8 + 3i) = x² - 16x + 64 + 9i² = x² - 16x + 55.
Then the polynomial can be written as follows:
x^4 - 16x³ + 70x² + 48x - 219 = (ax² + bx + c)(x² - 16x + 55).
As a fourth order polynomial can be the product of two second order polynomials. Applying the distributive property to the right side of the equality, we have that:
x^4 - 16x³ + 70x² + 48x - 219 = ax^4 + x³(b - 16a) + x²(55a + c - 16b) + x(55b - 16c) + 55c.
Then the coefficients are given as follows:
a = 1.55c = -219 -> c = -219/55 -> c = -3.98.b - 16a = -16 -> b = 0.Hence the other two factors are given as follows:
x² - 3.98 = 0
x = ± sqrt(3.98)
x = ± 1.995.
The linear factors are:
(x - x')(x - x'')(x - x''')(x - x'''').
In which x', x'', x''' and x'''' are the roots.
The solutions to f(x) = 0 are the roots.
More can be learned about the zeros of a polynomial at https://brainly.com/question/19030198
#SPJ1
Why does the graph y= sin(c) continue to go up and down rather than diverge to
like the graph of a quadratic, exponential, or any other function.
Answers
Answer:C. They have the same y-intercept and the same end behavior as x approaches
Step-by-step explanation:
What is the length of EF in the right triangle below?
D
26
10
E
F
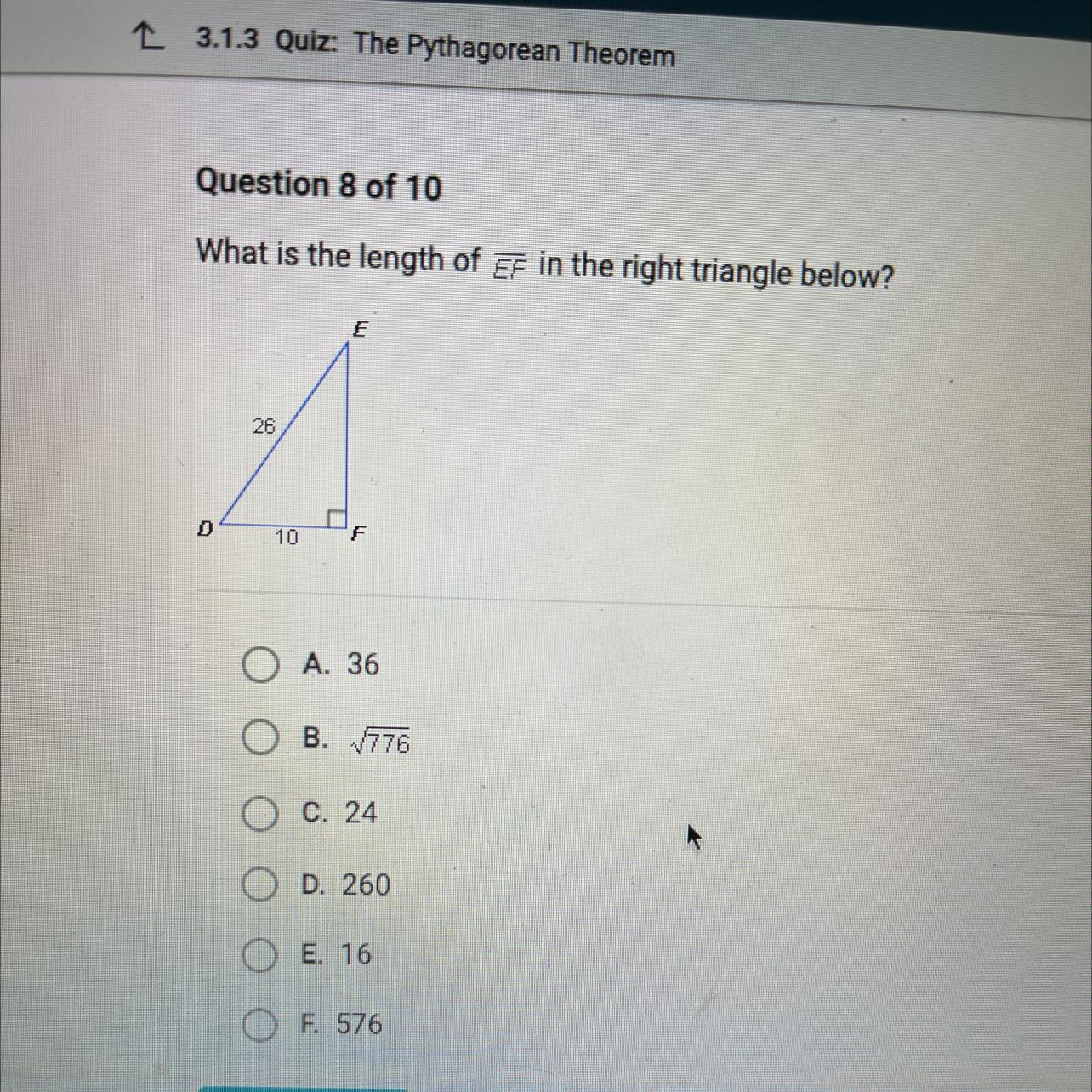
Answers
The measure of side length EF in the right triangle is 24.
What is the measure of side length EF?The Pythagorean theorem states that the "square on the hypotenuse of a right-angled triangle is equal in area to the sum of the squares on the other two sides.
It is expressed as;
c² = a² + b²
From the diagram:
Hypotenuse DE = c = 26
Leg DF = a = 10
Leg EF = b = ?
Plug in the values and solve for b:
c² = a² + b²
26² = 10² + b²
676 = 100 + b²
b² = 676 - 100
b² = 576
b = +√576 ( we take the positive value since we are dealing with dimensions)
b = 24
Therefore, the length EF is 24.
Option C)24 is the correct answer.
Learn more about Pythagorean theorem here: brainly.com/question/343682
#SPJ1
Suppose that you are testing the hypotheses Upper H 0 : pequals 0.43 vs. Upper H Subscript Upper A : pgreater than 0.43. A sample of size 150 results in a sample proportion of 0.48 . a) Construct a 99 % confidence interval for p. b) Based on the confidence interval, can you reject Upper H 0 at alpha equals0.005 ? Explain. c) What is the difference between the standard error and standard deviation of the sample proportion? d) Which is used in computing the confidence interval?
Answers
Answer:
Following are the answer to the given points.
Step-by-step explanation:
In point a:
The confidence interval for p is 95%
using formula:
\(= \hat P - Z\times \sqrt{\frac{\hat P(1- \hat P)}{n}} < p < \hat P +Z \times \sqrt{\frac{\hat P(1- \hat P)}{n}}\)
\(= 0.28 - 1.96 \times \sqrt {\frac{(0.28 \times 0.72)}{350} } < p < 0.28 + 1.96 \times \sqrt{(\frac{0.28 \times 0.72)} { 350}}\\\\= 0.233 < p < 0.327\)
In point b:
Because 0.22 is not within the trust interval, they have enough proof of H0 at level 0.05.
In point c:
For the percentage for samples,
\(\text{Standard error} = \sqrt { \frac{P (1 - p)}{n} }\) from ratio p
\(\text{Standard deviation} = \sqrt{ \frac{\hat{p}( 1 - \hat{p})}{n} }\) from sample ratio \(\hat{p}\)
In point d:
Standard deviation is used to measure the interval of confidence
\(\text{Standard deviation} = \sqrt{ \frac{\hat{p}( 1 - \hat{p})}{n} }\)
If the area of a square inscribed in a circle is
25, what is the area of the circle?
Answers
The area of a square inscribed in a circle is 25, then the area of the circle is 25π/2 or approximately 39.27 square units.
To solve this problem, we can use the relationship between the area of a square inscribed in a circle and the area of the circle itself.
When a square is inscribed in a circle, the diagonal of the square is equal to the diameter of the circle. Let's assume that the side length of the square is 's' and the radius of the circle is 'r'.
We are given that the area of the square is 25, so we can find the side length of the square:
Area of square = \(s^2 = 25\)
Taking the square root of both sides, we get:
s = √25 = 5
Since the diagonal of the square is equal to the diameter of the circle, we can find the diameter of the circle:
Diagonal = Diameter = s√2 = 5√2
The radius of the circle is half the diameter, so:
Radius = 5√2 / 2 = (5√2)/2
Now, we can calculate the area of the circle using the formula:
Area of circle = \(\pi r^2\)
Substituting the value of the radius, we get:
Area of circle = π((5√2)/\(2)^2\) = π(25/2) = 25π/2
Therefore, the area of the circle is 25π/2 or approximately 39.27 square units.
For more question on square visit:
https://brainly.com/question/428672
#SPJ8
The grade received on a certain teacher's 100-point test varies in direct proportion to the amount of time a student spends preparing for the test. If a student receives 72 points on a test for which she spent 3 hours preparing, what score would she receive on the next test if she spent 4 hours preparing?
Answers
Answer:
She would receive 96 points
Step-by-step explanation:
The grade (Y) received on a certain teacher's 100-point test varies in direct proportion to the amount of time(t) a student spends preparing for the test.
Mathematically
Y= kt
Where k is constant of proportionality
If y= 72 and t= 3
72=k3
72/3= k
24= k
So
Y= 24t
If t= 4
Y= kt
Y= 24(4)
Y= 96
Y = 96 points
She would receive 96 points
8).
9).
7). Degrees
Degrees
Degrees
A
77
Teacrerit20
HELP ASAP PLEASE

Answers
8. x= 28
9. x= 26
Answer:
1) 47 degrees
2) 28 degrees
3) 26 degrees
Step-by-step explanation:
a triangle always equals 180 degrees, you add together the numbers you have then subtract it from 180 then you'll get your answer <3
What is the sum of the geometric series
10
∑6(2)^n ?
N-1
A.15,658
B.6,138
C12,276
D756
Answers
The sum of the geometric series is -12,276.
So, the correct answer is C. -12,276.
To find the sum of the geometric series, we can use the formula:
\(S = a \times (1 - r^n) / (1 - r),\)
where S is the sum of the series,
a is the first term,
r is the common ratio, and
n is the number of terms.
In this case, the first term (a) is 6(2) = 12, the common ratio (r) is 2, and the number of terms (n) is 10.
Plugging these values into the formula, we get:
\(S = 12 \times (1 - 2^{10} ) / (1 - 2).\)
Calculating further:
\(S = 12 \times (1 - 1024) / (-1) = 12 \times 1023 = 12276.\)
Therefore, the sum of the geometric series is -12,276.
So, the correct answer is C. -12,276.
For similar question on geometric series.
https://brainly.com/question/24643676
#SPJ11
A regular hexagonal prism has a height of 7 cm and base edge length of 4 cm. Identify its lateral area and surface area. HELP ASAP
Answers
Answer:
Lateral Surface Area = 168 \(cm^2\)
Total Surface Area = 209.57 \(cm^2\)
Step-by-step explanation:
Given:
There is a regular hexagonal prism with
Height, h = 7 cm
Base edge length, a = 4 cm
To find:
Lateral surface area and total surface area = ?
Solution:
Formula for lateral surface area is given as:
\(LSA = \text{Perimeter of Base}\times Height\)
Perimeter of a hexagon is given as:
\(P = 6 \times Edge\ Length\\\Rightarrow P = 6\times 4=24\ cm\)
Now, LSA = 24 \(\times\) 7 = 168 \(cm^2\)
Total Surface area of prism is given by the formula:
\(TSA = LSA + B\)
where B is the area of base.
Base is a regular hexagon, formula for area of a regular hexagon is given by:
\(B =6\times \dfrac{\sqrt3}4\times Edge^2\\\Rightarrow B =6\times \dfrac{\sqrt3}4\times 4^2 = 24\sqrt3\ cm^2\\\Rightarrow B = 41.57 cm^2\)
So, Total Surface Area = 168 + 41.57 = 209.57\(cm^2\)
So, answer is :
Lateral Surface Area = 168 \(cm^2\)
Total Surface Area = 209.57 \(cm^2\)
Answer: It' actually:
Lateral Area: 168cm²
Surface Area: 251.1cm²
Hope this helps ya!
If nobody answers me imma just die
Cause I know I’m nothing cause nobody will help

Answers
Answer:
when reflected across the y-axis the points will reflect onto the other side on the y-axis.
when reflected over the x-axis the points with reflect onto the x-axis
which statement explains why ABC is congruent to A’B’C’?

Answers
The distance of all the side of ΔABC and ΔA'B'C' are equal which makes them congruent triangles.
What is congruent triangles?
When all 3 corresponding sides and every one 3 corresponding angles area unit equal in size, 2 triangles area unit aforementioned to be congruent.
Main Body:
First let us find the co-ordinates of both the triangles.
A= (3,5)
B = (-2, 3)
C= (-4,-1)
A' =(10,-5)
B'= (5, -3)
C' =(3,1)
Distance between two points = d=√((x₂ – x₁)² + (y₂ – y₁)²).
In ΔABC
Distance of side AB = √((3 –(-2) )² + (5 –3 )²)
= √5² +2²
= √29
Distance of side BC = √((-2-(-4) )²+ (3 -(-1 )²)
= √20
Distance of side CA = √((3-(-4) )² + (5-(-1) )²)
= √7² + 6²
= √85
Distance of side A'B' = √((10 -5)² + (-5-(-3))²
= √(5² +2²)
= √29
Distance of side B'C' = √ ((5-3)² + (-3 -1)² )
= √ (2)² +4²
= √20
Distance of side C'A' = √((10-3)² + ( -5-1)²)\
= √(7)² + 6²
= √85
This shows each side of ΔABC is equal to side of ΔA'B'C'.
hence the triangles are congruent.
To learn more about congruent , visit;
https://brainly.com/question/2938476
#SPJ9
find the slope and y-intercept.
Answers
The slope and the y-intercept of the line y = 4x + 5 are given as follows:
Slope of 4.y-intercept of 4.How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b
The coefficients m and b represent the slope and the intercept, respectively, and are explained as follows:
m represents the slope of the function, which is by how much the dependent variable y increases or decreases when the independent variable x is added by one.b represents the y-intercept of the function, representing the numeric value of the function when the input variable x has a value of 0. On a graph, the intercept is given by the value of y at which the graph crosses or touches the y-axis.The function for this problem is given as follows:
y = 4x + 5.
Hence the slope and the intercept are given as follows:
m = 4.b = 5.Missing InformationThe problem asks for the slope and the intercept of y = 4x + 5.
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ1
design and implement an application that reads in a set of values in the range of 1 to 100 (yes, you should error check for this) and then creates a chart showing how often the values appeared. the chart should look like the one below and should show how many values fell in the range of 1-10, 11-20, 21-30, and so on.
Answers
Sample Output: Code to copy: //Import the required package. import java.util.Scanner; //Define the class Main. class Main { //Start the execution of the main() method.
Code of Origin:Origin C is a programming language that is ANSI C compatible and also incorporates C++ and C# features. The majority of Origin objects can be accessed programmatically thanks to built-in C++ classes. The NAG C Library's extensive collection of numerical computational routines is also included.
C, a replacement for the programming language B, was initially created by Ritchie at Bell Labs between 1972 and 1973 to create utilities for Unix. It was used to re-implement the Unix operating system's kernel. C increasingly gained popularity in the 1980s.
import java.io.*;
import java.util.Scanner;
public class histogram
{
public static void main(java.lang.String[] args)
throws IOException
{
Scanner scan = new Scanner (System.in);
final int min = 1;
final int max = 10;
final int limit = 10;
int[] a = new int[max];
for (int b = 0; b < a.length; b++)
{
a[b] = 0;
}
System.out.println("Enter Number between 1 and 100: \n (Or press 0 to stop)");
int number = scan.nextInt();
while (number >= min && number <= (limit*max) && number != 0)
{
a[(number-1)/limit] = a[(number - 1 ) / limit] + 1;
System.out.print("Please enter a value:");
number = scan.nextInt();
}
System.out.println("\n__Histogram__");
for (int y = 0; y < a.length; y++)
{
System.out.print(" " + (y * limit + 1) + " - " + (y + 1) * limit + "\t");
return;
}
for (int z = 0; z < a[b]; z++)
{
System.out.print("*");
}
System.out.println(0);
}
}
To learn more about Histogram refer to:
https://brainly.com/question/25983327
#SPJ4
Ir[ Fairbanks, the temperature at 6:00 AM on Sunday is - 48°F. The weather forecast
predicts that a warming trend will raise the temperature to 0°F.
If the temperature rises an average of 16° a day, how many days will it take to get to 0?
Answers
Answer:
The answer is 3 days
Step-by-step explanation:
Divide 48/16=3
the value of √-9 is not -3 because...?

Answers
Because \(-3^{2} \neq -9\)
A number squared never equals a negative number. So that's why the value of \(\sqrt{-9}\) is not -3.
Hope this helps you!
~Just a joyful teen
\(SilentNature\)
If you really genius please answer this with solution ASAP

Answers
Answer:
sinn
Step-by-step explanation:
sine
PLS HELP! it’s question 12

Answers
Answer:
yes
Step-by-step explanation:
it is going by 5s.
Answer:
Yes. This is because if you plot the numbers on a ration table or see the graph points, you can see a pattern: you multiply by 5. The equation to solve this would be y=5x. Another reason why this is proportional is that the graph starts from the origin (0,0) This is the opposite for non-proportional relationships. Hope this helps! :)
The sum of a number and -16 is 25. Find the number.
A.
25/16
B. -9
C.
41
D. 9
please help :)
Answers
Answer:
41
Step-by-step explanation:
n+(-16)=25
n-16=25
Add 16 to both sides to isolate the variable
n=41
Answer:
\( \huge{ \fbox{ \sf{41}}}\)
Step-by-step explanation:
\( \star{ \sf{ \: Let \: the \: missing \: number \: be \: x}}\)
Create an equation
\( \sf{x + ( - 16) = 25}\)
\( \mapsto{ \sf{x - 16 = 25}}\)
Move 16 to right hand side and change it's sign
\( \mapsto{ \sf{x = 25 + 16}}\)
Add the numbers : 25 and 16
\( \mapsto{ \sf{x = 41}}\)
The number is 41
Hope I helped!
Best regards! :D
~TheAnimeGirl
what is g÷10 pls explain it
Answers
Answer:
answer may be 0.1g or 1/10g

A 2 meter television camera at ground level is filming the lift-off of a space shuttle at a point 750 meters from the launch pad. The camera’s angle of elevation to the shuttle is 32° at this specific time . Find the height of the shuttle.
Answers
To find the height of the shuttle, we can use trigonometry and the concept of similar triangles. The height of the shuttle is approximately 468.675 meters.
Let's assume that the height of the shuttle is represented by 'h' meters. From the information given, we know that the distance between the camera and the launch pad is 750 meters, and the angle of elevation from the camera to the shuttle is 32 degrees.
Using trigonometry, we can set up the following equation:
tan(32°) = h / 750
To find the value of h, we can rearrange the equation:
h = tan(32°) * 750
Using a calculator, we can find the value of tan(32°) ≈ 0.6249.
Now we can calculate the height of the shuttle:
h ≈ 0.6249 * 750
h ≈ 468.675 meters
Therefore, the height of the shuttle is approximately 468.675 meters.
For more such questions on trigonometry
https://brainly.com/question/24349828
#SPJ8
21) Kinzang is 1.49 m tall. He was 0.53 m at birth. How much did he grow?
Answers
Kinzang grew 0.96 meters.
We have,
To find how much Kinzang grew, we need to subtract his height at birth from his current height:
Height Kinzang grew = Current height - Height at birth
Height Kinzang grew = 1.49 m - 0.53 m = 0.96 m
Therefore,
Kinzang grew 0.96 meters.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ1
What values of b satisfy 3(2b + 3)² = 36?
Answers
Answer:
The values of b that satisfy the equation are:
b = (2√3 - 3) / 2
b = (-2√3 - 3) / 2
In other words, b can take the values (2√3 - 3) / 2 or (-2√3 - 3) / 2.
Step-by-step explanation:
To find the values of b that satisfy the equation 3(2b + 3)² = 36, we can solve for b by following these steps:
1. Divide both sides of the equation by 3:
(2b + 3)² = 12
2. Take the square root of both sides:
√[(2b + 3)²] = √12
Simplifying further:
2b + 3 = ±√12
3. Subtract 3 from both sides:
2b = ±√12 - 3
4. Divide both sides by 2:
b = (±√12 - 3) / 2
Simplifying further:
b = (±√4 * √3 - 3) / 2
b = (±2√3 - 3) / 2
Therefore, the values of b that satisfy the equation are:
b = (2√3 - 3) / 2
b = (-2√3 - 3) / 2
In other words, b can take the values (2√3 - 3) / 2 or (-2√3 - 3) / 2.
Ad
Module 3 Mini Project
While there were about 3,000,000 people (about the population of Arkansas)
who visited the zoo last year, the number of people who visited in each
month was different. For example, people are more likely to visit the zoo in
July than they are in January. For that reason, the zoo raises its prices during
the months when there are a lot of visitors (peak season) and lowers its
prices during the months when there are not as many visitors (off season).
During peak season the zoo has about 1,800,000 visitors. Write an
expression to show how much money would be made during peak season
where p is the price of one peak season ticket.
The zoo wants to sell tickets in the off season for half of the price of tickets
in the peak season. Write an expression to show how much money would be
made during the off season where p is the price of one peak season ticket.
To break even the zoo needs to make at least how much money they spent
on the animals. Write and solve an inequality to find out how much the price
of one peak season ticket should be where p is the price of one peak season
ticket. How much should one off season ticket be?
Answers
Money made during peak season = 1,800,000 * p
1. Expression for money made during peak season:
During peak season, the zoo has about 1,800,000 visitors. To calculate the money made during peak season, we multiply the number of visitors by the price of one peak season ticket (p):
Money made during peak season = 1,800,000 * p
2. Expression for money made during the off season:
The zoo wants to sell tickets in the off season for half the price of tickets in the peak season. Therefore, the price of one off season ticket would be p/2. To calculate the money made during the off season, we multiply the number of visitors by the price of one off season ticket:
Money made during the off season = 1,200,000 * (p/2) = 600,000 * p
3. Inequality for breaking even:
To break even, the zoo needs to make at least as much money as they spent on the animals. Let's represent the amount spent on animals as A. The money made during peak season plus the money made during the off season should be greater than or equal to the amount spent on animals:
1,800,000 * p + 600,000 * (p/2) ≥ A
Simplifying the inequality:
3,600,000p + 300,000p ≥ 2A
3,900,000p ≥ 2A
Solving for p:
p ≥ (2A) / 3,900,000
This determines the minimum price of one peak season ticket to break even.
The price of one off season ticket would be half the price of one peak season ticket, so the off season ticket should be (p/2).
For more such questions on season, click on:
https://brainly.com/question/25000811
#SPJ8
3(y+1/4)>3/4 determine the value of y for the inequality
Answers
Therefore, the solution to the inequality 3(y + 1/4) > 3/4 is y > 0.
What is inequality?An inequality is a mathematical statement that shows a relationship between two values, which are not necessarily equal. Inequalities are represented using symbols such as > (greater than), < (less than), ≥ (greater than or equal to), and ≤ (less than or equal to). Inequalities are commonly used in algebra and other areas of mathematics, as well as in real-world applications such as finance, economics, and science. They can be used to represent constraints or limits on a variable, such as the maximum or minimum value that it can take.
Here,
We can solve the inequality 3(y + 1/4) > 3/4 by first distributing the 3 to the expression inside the parentheses:
3y + 3/4 > 3/4
Next, we can simplify by subtracting 3/4 from both sides:
3y > 0
Finally, we can solve for y by dividing both sides by 3:
y > 0/3
y > 0
To know more about inequality,
https://brainly.com/question/30238773
#SPJ1
Mauro has 140 feet of rope he will cut it into two peices so that the length of the longer peice is 3 times the length of the shorter peice
Answers
Explain how to find 20% of 160
Answers
Answer: 20% of 160 is 32.
Step-by-step explanation:
The percentage is from the word percent which means one part in a hundred. It is a part of the base or the whole determined by the rate. Usually, the percentage is smaller than the base. However, there are also cases where the percentage is greater than the base. This happens when the percent is greater than 100%.
To find the percentage, you have to multiply the base and the rate. The base is the 100% or original amount or the whole while the rate is the ratio of the percentage to the base and it has the percent sign (%). Remember that you have to convert the rate to a decimal number by moving the decimal point twice to the left.
Let us now find the 20% of 160.
20% = 0.2
percentage = 160 × 0.2
= 32
Given sinz = -4/5 for pi < z < (3pi)/2, find the value of cosz.

Answers
The angle z is in the third quadrant, the value of cosz is negative. Hence, cosz = -3/5.So, the value of cosz is -3/5.
Given sinz = -4/5 for pi < z < (3pi)/2, we need to find the value of cosz. We can use the trigonometric identity of Pythagorean theorem to find the value of cosz.
According to Pythagorean theorem, sin2θ + cos2θ = 1, where θ is the angle in the right-angled triangle and sin, cos are the trigonometric ratios.
The negative sign for the given sinz indicates that the angle z is in the third quadrant. So, we can take the help of the unit circle to find the value of cosz as shown below:
Here, we have used the Pythagorean identity of sin2z + cos2z = 1 on the unit circle to find the value of cosz. Since the value of sinz is already given, we can find the value of sin2z as: sin2z = sinz x sinz = (-4/5) x (-4/5) = 16/25
Then, we can substitute the value of sin2z in the Pythagorean identity as: cos2z = 1 - sin2z = 1 - (16/25) = 9/25We need to find the value of cosz.
So, we can take the square root of cos2z as: cosz = ±(√(9/25)) = ±(3/5)The sign of cosz can be determined by considering the quadrant of the angle z.
Since the angle z is in the third quadrant, the value of cosz is negative. Hence, cosz = -3/5.So, the value of cosz is -3/5.
For more questions on angle.
https://brainly.com/question/31615777
#SPJ8
It is advertised that the average braking distance for a small car traveling at 65 miles per hour equals 122 feet. A transportation researcher wants to determine if the statement made in the advertisement is false. She randomly test drives 38 small cars at 65 miles per hour and records the braking distance. The sample average braking distance is computed as 116 feet. Assume that the population standard deviation is 21 feet. (You may find it useful to reference the appropriate table: z table or t table) a. State the null and the alternative hypotheses for the test.
Answers
Complete Question
The complete question is shown on the first uploaded image
Answer:
the null hypothesis is \(H_o : \mu = 122\)
the alternative hypothesis is \(H_a : \mu \ne 122\)
The test statistics is \(t = - 1.761\)
The p-value is \(p = P(Z < t ) = 0.039119\)
so
\(p \ge 0.01\)
Step-by-step explanation:
From the question we are told that
The population mean is \(\mu = 122\)
The sample size is n= 38
The sample mean is \(\= x = 116 \ feet\)
The standard deviation is \(\sigma = 21\)
Generally the null hypothesis is \(H_o : \mu = 122\)
the alternative hypothesis is \(H_a : \mu \ne 122\)
Generally the test statistics is mathematically evaluated as
\(t = \frac { \= x - \mu }{\frac{ \sigma }{ \sqrt{n} } }\)
substituting values
\(t = \frac { 116 - 122 }{\frac{ 21 }{ \sqrt{ 38} } }\)
\(t = - 1.761\)
The p-value is mathematically represented as
\(p = P(Z < t )\)
From the z- table
\(p = P(Z < t ) = 0.039119\)
So
\(p \ge 0.01\)

slope-intercept form? proper fractions, and improper

Answers
Answer:
y = 3x
Step-by-step explanation:
slope intercept form is y = mx + b with m as the slope and b as the y-intercept
to find the slope you can see where the line intersects at (1, 3) and (0,0) If you look at the graph you count up three spaces over one so the slope is 3
since the y-intercept intersects at (0,0) The y-intercept is 0 and you do not have to add that to the answer
Answer:
y=3x I think if not sorry
Step-by-step explanation:
have great evening,day,night,morning!