Answers
Answer: X = 24.5.
Both angles are the same size, so 42=2x-7. You then add 7 to both sides to make 49=2x, then you divide by 2 to get 24.5 = x
Hope this helped :)
Related Questions
Which sentence contains a gerund phrase?
The goal of the class was learning how to use a computer keyboard.
Washing clothes regularly allows Annabelle to always have something clean to wear.
To sing with the Metropolitan Opera has been my dream throughout my life.
Troubled by the noise from the trains, Cole began to wear sound-muting headphones.
Answers
Answer:
its b
Step-by-step explanation:
i took the test
Answer: its b cause i took the test and got it right
Write a system of inequalities to match the graph and prove that the coordinate point (-10, -14) is in the solution set

Answers
Answer:
y < x - 2
y ≥ 2x + 5
Step-by-step explanation:
For the equation of the dotted line,
Slope of the line = \(\frac{y_2-y_1}{x_2-x_1}\)
Since the dotted lines passes through the points (-7, -9) and (2, 0)
Slope = \(\frac{-9-0}{-7-2}\)
\(m_1\) = 1
Therefore, equation of the line passing through (2, 0) and slope = 1 will be,
y - y' = m₁(x - x')
y - 0 = 1(x - 2)
y = x - 2
Since, shaded area is below the dotted line,
y < x - 2 will be the inequality.
Slope of the solid line passing through (-7, -9) and (0, 5) is,
\(m_2=\frac{-9-5}{-7-0}\)
= 2
Therefore, equation of the line passing through (0, 5) and slope = 2 will be,
y - 5 = 2(x - 0)
y = 2x + 5
Since, the given line is a solid line and shaded area is above the line,
y ≥ 2x + 5 will be the inequality.
Since, (-10, -14) is lying in the common shaded area of both the inequalities, it will be the solution set of the graphed inequalities.
Where is the central tendency located in a skewed left distribution?
to the left of the tallest bar
to the right of the smallest bar
to the left of the smallest bar
in the center of the graph
to the right of the tallest bar
Answers
The Central tendency is typically located to the right of the tallest bar.
In a skewed left distribution, the central tendency is typically located to the right of the tallest bar. Skewed left distributions, also known as negatively skewed distributions, are characterized by a tail that extends towards the left side of the distribution.
The central tendency refers to the measure that represents the center or average of a distribution. It provides information about the typical or central value around which the data points tend to cluster. Common measures of central tendency include the mean, median, and mode.
In a skewed left distribution, the mean is usually influenced by the long tail on the left side of the distribution. This tail pulls the mean towards lower values, resulting in a lower mean compared to the median. Therefore, the mean will typically be located to the left of the tallest bar in a skewed left distribution.
On the other hand, the median is less affected by the skewness of the distribution and is relatively robust to extreme values. It represents the value that separates the lower 50% of the data from the upper 50%. In a skewed left distribution, the median will be located closer to the tallest bar or even slightly to the right of it.
The mode, which represents the most frequently occurring value in a distribution, may or may not be influenced by the skewness depending on the shape of the distribution. It can be located anywhere along the distribution, and its position is not necessarily tied to the location of the tallest bar.
To summarize, in a skewed left distribution, the central tendency is typically located to the right of the tallest bar. The median is usually closer to the tallest bar or slightly to the right, while the mean is influenced by the skewness and tends to be located to the left of the tallest bar.
To know more about Central tendency.
https://brainly.com/question/1288901
#SPJ8
3 Jack walk from Santa Clara to Polo Allo. Il took I hour 25 min to walk from Santa Clot to Los Altos. Than it took 25 minute of wal from los altos to Palo buto. He arrived in Palo alto at 2:45 P.M. of what time die Santa Clara ? he leave Santa clara
Answers
The time Jack left Santa Clara is 1 : 55 pm
What is word problem?A word problem in math is a math question written as one sentence or more. These statements are interpreted into mathematical equation or expression.
The time for Jack to walk to lose Altos is 25 min and he uses another 25mins to work to Palo alto.
Therefore, the total time he spent is
25mins + 25 mins = 50 mins
He arrived Palo at 2 :45 pm, therefore the time he left Santa Clare will be ;
2:45 pm = 14 :45
= 14:45 - 50mins
= 13:55
= 1 : 55pm
Therefore he left at 1:55 pm
learn more about word problem from
https://brainly.com/question/21405634
#SPJ1
how do i determine which of these fit the graph data?d(t)=50t+300d(t)=50td(t)=-50t+300d(t)=-50t
Answers
To determine the behavior of the graph, we calculate the slope-intercept form of the graph. It is given by
y = mx + b
Here, b is the y-intercept.
m is the slope of the graph that is the difference between y-axis over x-axis.
m = (y2 - y1) / (x2 - x1)
To calculate both points, let's pick two points from the graph.
For example, the first point is (1, 250) and the second point is (2, 200)
So,
(x1, y1) = (1, 250)
x1 = 1
y1 = 250
(x2, y2) = (2, 200)
x2 = 2
y2 = 200
Now, put these values in slope form, we get
m = (200 - 250) / (2 - 1)
m = -50
Hence, the slope is -50 that tells that with every on increase in the value of x, y is decreasing 50. Hence, if I decrease the value of x, y will rise 50.
Therefore,
I can say that when x = 0, y = 300. (0, 300)
Therefore, b = 300
Now, put all these values in the slope-intercept form.
y = mx + b
dt = -50x + 300
Hence, the 3rd option is correct.
Can some pls help me with this!

Answers
THATS A LOT
Step-by-step explanation:
4x + 7 − 23
In this expression, the coefficient is 4.
True or False
Answers
Answer:
True
Step-by-step explanation:
A rectangular poster is 50 centimeters long and 25 centimeters wide. If 1 centimeter is approximately 0.4 inches, which of the following best represents the area of the poster in inches?
Answers
The area of the poster in inches is,
⇒ A = 4 inches²
We have to given that;
A rectangular poster is 50 centimeters long and 25 centimeters wide.
Here, 1 centimeter is approximately 0.4 inches
Hence, Lenght = 50 cm
Lenght = 50 x 0.4
= 2 inches
Width = 25 cm
= 25 x 0.4
= 1 inches
Thus, The area of the poster in inches is,
⇒ A = 1 x 4
⇒ A = 4 inches²
Learn more about the rectangle visit:
https://brainly.com/question/2607596
#SPJ1
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
1
A reforestation drive is conducted in a town. The town had 2,022 trees at the start of the drive. Four months after the start of the
reforestation drive, the town had 4,897 trees.
If n represents the number of months and T represents the number of trees, which of the following equations can be used to model
this situation?
OA. T 718.75 - 2,022
OB. T = 2,022n + 718.75
OC. T 718.75 + 2,022
OD. T = 2875 + 2,022n
Answers
Answer: OD. T = 2875 + 2,022n
Step-by-step explanation: What makes the most sense is
OD. T = 2875 + 2,022n
because they added 2875 to the trees already there and 4,897 was the new total after four months, I also want to point out it has nothing to do with decimals or a 700 number.
What is half of 3/4 in fraction?
Answers
Answer:
3/8
Step-by-step explanation:
1/2 times 3/4= 3/8
Round 317,675 to the nearest ten thousand
Answers
Answer:320000
Step-by-step explanation:
Zack is on his school's color guard and is practicing throwing and catching his flag. He throws the flag into the air from a height of 5 feet at a velocity of 30 feet per second. After the flag starts to come back down, he catches it 7 feet above the ground.
To the nearest tenth of a second, how long is the flag in the air before Zack catches it?
Hint: Use the formula h=16t2+vt+s.
Answers
The Nearest tenth of a second, the flag is in the air for approximately 0.1 seconds before Zack catches it.
To determine the time the flag is in the air before Zack catches it, we can use the kinematic equation for vertical motion:
h = 16t^2 + vt + s
Where:
h is the height of the flag,
t is the time in seconds,
v is the initial vertical velocity of the flag,
s is the initial height of the flag.
In this case, the flag is thrown into the air from a height of 5 feet (s = 5) with an initial vertical velocity of 30 feet per second (v = 30). Zack catches it at a height of 7 feet (h = 7).
We can rewrite the equation as:
7 = 16t^2 + 30t + 5
To find the time (t) when the flag is at a height of 7 feet, we can rearrange the equation and solve for t. However, since this is a quadratic equation, we can also use the quadratic formula.
The quadratic equation in this case is:
16t^2 + 30t + 5 - 7 = 0
16t^2 + 30t - 2 = 0
Now, we can use the quadratic formula:
t = (-b ± √(b^2 - 4ac)) / (2a)
Applying the values from the quadratic equation, we have:
t = (-30 ± √(30^2 - 4 * 16 * (-2))) / (2 * 16)
Simplifying further:
t = (-30 ± √(900 + 128)) / 32
t = (-30 ± √1028) / 32
Using a calculator, we find two solutions:
t ≈ -1.08 seconds or t ≈ 0.06 seconds
Since time cannot be negative in this context, we discard the negative solution.
Therefore, to the nearest tenth of a second, the flag is in the air for approximately 0.1 seconds before Zack catches it.
To know more about Nearest .
https://brainly.com/question/31217836
#SPJ8
I need help please.

Answers
Step-by-step explanation:
if I had to guess it's probably true
The values of x shown on the number line below are solutions to an absolute valueequation.
Answers
We will use the solutions to the absolute value functions to determine the function's description as follows:
The two solutions to the absolute value function are given as follows:
\(x\text{ = -3 and x = 5}\)We will investigate each description as follows:
A) The distance of x from -3 is 8.
We will use the number line and determine the distance from ( x = -3 ) to the other solution ( x = 5 ). The number of units along the x-axis from point ( x = -3 ) to ( x = 5 ) would be:
\(\textcolor{#FF7968}{8}\text{\textcolor{#FF7968}{ units}}\)Hence, option A is correct!
B) This option describes the absolute value function as follows:
\(|\text{ x }-\text{ 3 | = 5}\)We will solve the above absolute value function as follows:
\(\begin{gathered} +(x\text{ - 3 ) = 5 OR -(x - 3 ) = 5} \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 8 }}\text{ OR }\text{\textcolor{#FF7968}{x = -2}} \end{gathered}\)The above solution to the absolute value function is not equal to the solution presented in the number line. Hence, option B is incorrect!
C) The distance of x from 1 is 4
The above statement describes the center point of the two solutions represented on the number line. We will determine the distance of each solution given from point ( x = 1 ) as follows:
\(\text{\textcolor{#FF7968}{Distance}}\text{ = 5 - 1 = 1 - ( - 3 ) = 4}\)We see that the distance from each solution ( x = -3 ) AND ( x = 5 ) from point ( x = 1 ) is 4 units along the x axis. Hence, option C is correct!
D) The distance of x from 4 is 1
The above statement describes the center point of the two solutions represented on the number line. We will determine the distance of each solution given from point ( x = 4 ) as follows:
\(\begin{gathered} \text{Distance : ( x = 5 ) - ( x = 4 ) = }\text{\textcolor{#FF7968}{1 unit}} \\ \text{Distance : ( x = -3 ) - ( x = 4 ) = }\text{\textcolor{#FF7968}{7 units}} \end{gathered}\)The above statement is true for the solution ( x = 5 ); however, incorrect for solution ( x = -3 ). Hence, we will reject this option D as it is not true in entirety!
E) This option describes the absolute value function as follows:
\(|\text{ x }-\text{ 4 | = }1\)We will solve the above absolute value function as follows:
\(\begin{gathered} +(x\text{ - 4 ) = 1 OR - ( x - 4 ) = }1 \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 5 }}\text{ OR }\text{\textcolor{#FF7968}{x = }}\textcolor{#FF7968}{3} \end{gathered}\)The above solution to the absolute value function is not equal to the solution presented in the number line. Hence, option E is incorrect!
F) This option describes the absolute value function as follows:
\(|\text{ x + 1 | = }4\)We will solve the above absolute value function as follows:
\(\begin{gathered} +(x\text{ + 1 ) = 4 OR - ( x + 1 ) = }4 \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 3 }}\text{ OR }\text{\textcolor{#FF7968}{x = -}}\textcolor{#FF7968}{3} \end{gathered}\)The above solution to the absolute value function is not equal to the solution presented in the number line. Hence, option F is incorrect!
G) The distance of x from -3 is 5
The above statement describes the center point of the two solutions represented on the number line. We will determine the distance of each solution given from point ( x = 4 ) as follows:
\(\begin{gathered} \text{Distance : ( x = 5 ) - ( x = -3 ) = }\text{\textcolor{#FF7968}{8 unit}} \\ \end{gathered}\)The above statement is not true for the solution ( x = 5 ). Hence, we will reject this option G as it is not true in entirety!
H) This option describes the absolute value function as follows:
\(|\text{ x }-\text{ 1 | = }4\)We will solve the above absolute value function as follows:
\(\begin{gathered} +(x\text{ - 1 ) = 4 OR - ( x - 1 ) = }4 \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 5 }}\text{ OR }\text{\textcolor{#FF7968}{x = -}}\textcolor{#FF7968}{3} \end{gathered}\)The above solution to the absolute value function is equal to the solution presented in the number line. Hence, option H is correct!
The correct statements are:
\(\textcolor{#FF7968}{A}\text{\textcolor{#FF7968}{ , C , H}}\)The above statement describes the center point of the two solutions represented on the number line. We will determine the distance of each solution given from point ( x = 4 ) as follows:
\(undefined\)Line B passes through the points (5, 10) and (0,0). What is the slope of the line perpendicular to line
B?

Answers
Answer:
-1/2 is the answer
Step-by-step explanation:
HELP ASAP PLEASE !!!!

Answers
Explanation: 32/3^2*5^3
1. Make the denominators equal (3^2*5^3), so that means you need to multiply 7 by 5 and 1 by 3.
2. Subtract 3 from 35 to get 32 on top.
Then, you’re done!
Help PLSSS
What is the volume of a cone with a diameter of 16 centimeters and a height of 15 centimeters?
The options:
480π cm^3
544π cm^3
320π cm^3
363π cm^3
Answers
Answer:
320π cm^3
Step-by-step explanation:
V=1/3 π r² h
V=1/3 × π x 8² x 15
V=1/3 × π x 64 x 15
V=320π cm³
L is the mid point of KM. If LM = 8x and KM = 9x + 7, what is LM?
Answers
The value of LM is 8 for the given line segment.
What is a line segment?A line section that can connect two places is referred to as a segment.
In other words, a line segment is just part of a big line that is straight and going unlimited in both directions.
The line is here! It extends endlessly in both directions and has no beginning or conclusion.
Given the line segment KM with midpoint L
So,
KL = LM
(KM - LM) = LM
9x + 7 - 8x = 8x
x + 7 = 8x
7x = 7
x = 1
Now,
LM = 8(1) = 8 unit.
Hence "The value of LM is 8 for the given line segment".
For more about line segment,
https://brainly.com/question/25727583
#SPJ1
There were 44 dogs and cats at the pet store if 75% were cats how many cats were at the pets store?
Answers
Answer:
33.
Step-by-step explanation:
75% x
100 44
x = (44 * 75 ) / 100 = 33.
What percentage of the food cost is the tip?
Answers
Winston earns $140.00 by selling 56 hot dogs at a concession stand at school. Using the same rate for the cost of one hot dog, how many hot dogs would Winston need to sell to earn a total of $175.00?
A. 14
B. 70
C.350
D.2.5
Answers
Answer:
B or 70 hot dogs.
Step-by-step explanation:
56 hot dogs cost 140 dollars
1 hot dog costs 140/56 = 2.50
How many hot dogs would you need to see to get 175 dollars.
x * $2.50 = $175
x = 175/2.5
x = 70
what is the 2 step equation -1=(5+x)6
Answers
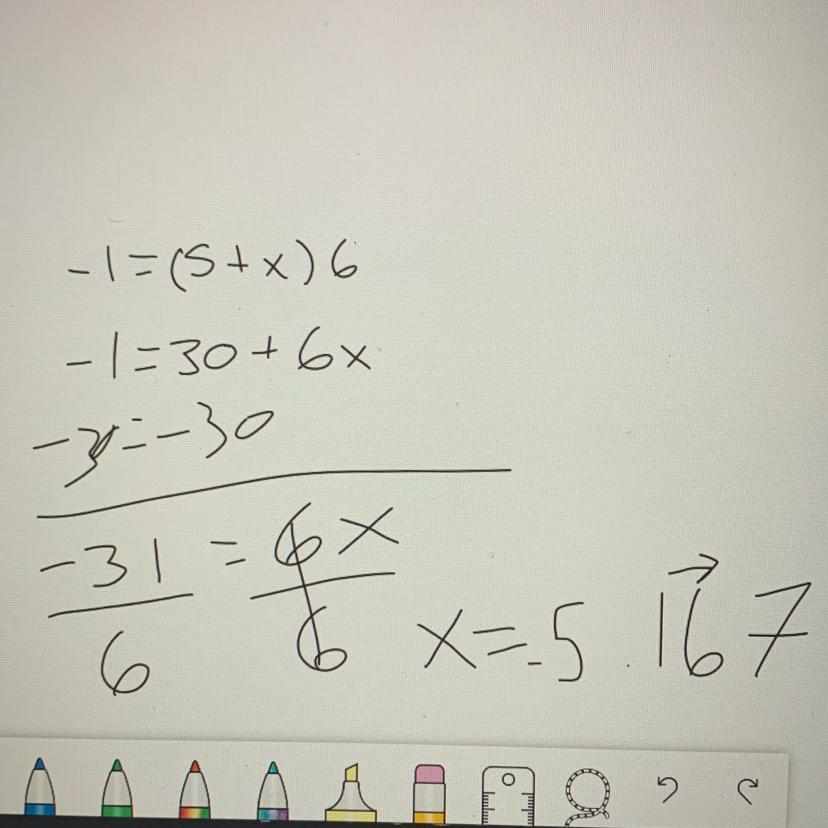
Archie bought 100 shares of stock in an ice cream company 2 years ago. He paid $60.65 per share. He just sold all of his shares for $67.68 per share. How much did he gain?
Answers
Answer:
Step-by-step explanation:
First, we need to find the difference between the price that he sold the shares for and the price that he bought them at: (67.68-60.65) = 7.03
That means that there was a gain of $7.03 per share for Archie.
That being said, since Archie bought 100 shares, we can multiply that number by 100 to find the total gain from selling the shares:
(7.03x100)= 703
The answer then is:
Archie gained $703 from selling all of his shares.
joan’s finishing time for the bolder boulder 10k race was 1.81 standard deviations faster than the women’s average for her age group. there were 410 women who ran in her age group. assuming a normal distribution, how many women ran faster than joan? (round down your answer to the nearest whole number.)
Answers
Given that Joan's finishing time was 1.81 standard deviations faster than the women's average for her age group, we can use the properties of a normal distribution to find the corresponding percentage.
Since Joan is faster than the average, her finishing time would fall in the top portion of the distribution. Using a standard normal distribution table or a calculator, we can find the percentage of data below her finishing time. The Z-score associated with 1.81 standard deviations is approximately 0.9641, which corresponds to a percentage of 96.41%.
This means that approximately 96.41% of the women in her age group ran slower than Joan. To find the number of women who ran faster, we subtract this percentage from 100%: 100% - 96.41% = 3.59%.
To determine the number of women, we multiply the percentage by the total number of women in her age group: 3.59% * 410 = 14.709.
Rounding down to the nearest whole number, we can conclude that approximately 14 women ran faster than Joan.
what is the equation for the perpendicular bisector of the line segment whose endpoints are (-7, 2) and (-1,-6)
Answers
The equation of the perpendicular bisector of the line segment with endpoints (-7, 2) and (-1, -6) is y = (3/4)x + 1.
To find the equation of the perpendicular bisector of a line segment, we need to determine the midpoint of the line segment and the slope of the line segment. The perpendicular bisector will have a negative reciprocal slope compared to the line segment and will pass through the midpoint.
Given the endpoints (-7, 2) and (-1, -6), we can find the midpoint using the midpoint formula:
Midpoint = ((x1 + x2)/2, (y1 + y2)/2)
Midpoint = ((-7 + (-1))/2, (2 + (-6))/2)
= (-8/2, -4/2)
= (-4, -2)
The midpoint of the line segment is (-4, -2).
Next, we need to find the slope of the line segment using the slope formula:
Slope = (y2 - y1)/(x2 - x1)
Slope = (-6 - 2)/(-1 - (-7))
= (-6 - 2)/(-1 + 7)
= (-8)/(6)
= -4/3
The slope of the line segment is -4/3.
Since the perpendicular bisector has a negative reciprocal slope, the slope of the perpendicular bisector will be 3/4.
Now, we can use the midpoint (-4, -2) and the slope 3/4 in the point-slope form of a line to find the equation of the perpendicular bisector:
y - y1 = m(x - x1)
y - (-2) = (3/4)(x - (-4))
y + 2 = (3/4)(x + 4)
y + 2 = (3/4)x + 3
y = (3/4)x + 1.
For more such questions on Line segment:
https://brainly.com/question/2437195
#SPJ8
The pH scale measures how acidic or basic a substance is. Bleach is said to have a
55 POINTS!!! WILL MARK!!! ANSWER FAST!!!pH of less than 14 and greater than 11. Model the normal range of pH values of bleach, using a compound inequality.
11 > x > 14
11 < x < 14
11 ≤ x ≤ 14
11 ≥ x ≥ 14
Answers
Answer:
11 < x < 14
Step-by-step explanation:
Bleach ph value ranges from 11-13
Help for Pre Calc please

Answers
The correct statement regarding the inverse function of f(x) = 4x^4 is given as follows:
\(f^{-1}(x) = \pm \left(\frac{x}{4}\right)^{\frac{1}{4}}\); f^(-1)(x) is not a function.
How to obtain the inverse function?The function in this problem is defined as follows:
f(x) = 4x^4.
To obtain the inverse of a function y = f(x), first the variables y and x are exchanged, as follows:
x = 4y^4.
Isolating the variable y, we have that:
y^4 = (x/4).
The inverse operation of the fourth power is the fourth root, hence:
\(y = \pm \sqrt[4]{\frac{x}{4}}\)
\(f^{-1}(x) = \pm \sqrt[4]{\frac{x}{4}}\)
\(f^{-1}(x) = \pm \left(\frac{x}{4}\right)^{\frac{1}{4}}\)
The plus/minus symbol means that for each input of x, the inverse function gives two outputs, meaning that there are multiple outputs mapped to each input, and thus the inverse is not a function.
This means that the second statement is correct.
More can be learned about inverse functions at https://brainly.com/question/3831584
#SPJ1
Which method would determine the volume of the prism shown below?
2-¹ cm
5 cm
2 cm
O
10 unit cubes and 10 one-quarter cubes gives 10+ (10x)
30 unit cubes and 10 one-quarter cubes gives
20 unit cubes and 10 one-quarter cubes gives 20+ 10x
¹+(10x) a
a
as the volume.
20+/1
as the volume.
+ (10x²1²) 251
as the volume.

Answers
The method that determines the volume of the prism is simply multiply the area of the base by the height, and the result is 12.5 cm³. (option-a)
To determine the volume of the prism shown in the diagram, we need to multiply the area of the base by the height.
The base of the prism is a rectangle with dimensions 5 cm by 2 cm. Therefore, the area of the base is:
A = length x width = 5 cm x 2 cm = 10 cm²
The height of the prism is 2-¹ cm, which is equivalent to 5/4 cm.
Therefore, the volume of the prism is:
V = A x h = 10 cm² x 5/4 cm = 12.5 cm³
The expressions involving unit cubes and one-quarter cubes are not relevant to this problem and do not provide a method for finding the volume of the prism.
For such more questions on volume
https://brainly.com/question/1972490
#SPJ8
A room has a floor dimension of 30 feet by 50 feet. The height of the basement is 6 feet. What is the total area of all four walls?
Answers
Answer:
960 feet
Step-by-step explanation:
30×6=180
180×2=360
50×6=300
300×2=600
360+600=960
