I think it's c but not sure
Given the following function and the transformations that are taking place, choose the most appropriate statement below regarding the graph of f(x) = 5 sin[2 (x - 1)] +4 Of(x) has an Amplitude of 5. a
Answers
The function can be graphed by first identifying the midline, which is the vertical shift of 4 units up from the x-axis, and then plotting points based on the amplitude and period of the function.
The amplitude of the function f(x) = 5 sin[2 (x - 1)] + 4 is 5.
This is because the amplitude of a function is the absolute value of the coefficient of the trigonometric function.
Here, the coefficient of the sine function is 5, and the absolute value of 5 is 5.
The transformation that is taking place in this function is a vertical shift up of 4 units.
Therefore, the appropriate statement regarding the graph of the function is that it has an amplitude of 5 and a vertical shift up of 4 units.
The function can be graphed by first identifying the midline, which is the vertical shift of 4 units up from the x-axis, and then plotting points based on the amplitude and period of the function.
To know more about function visit:
https://brainly.com/question/30721594
#SPJ11
Related Questions
Help!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!11

Answers
Use the note that Linear pairs have sum 180°
TD is a straight line\(\\ \rm\rightarrowtail m\overset{\frown}{CD}+122=180\)
\(\\ \rm\rightarrowtail m\overset{\frown}{CD}=180-122=58°\)
Now
DB arc be xA whole angle is 360° or 2π\(\\ \rm\rightarrowtail x+122+58+90=360\)
\(\\ \rm\rightarrowtail x+270=360\)
\(\\ \rm\rightarrowtail m\overset{\frown}{DB}=90°\)
Answer:
90
Step-by-step explanation:
A panel of judges must be chosen to judge the upcoming dance competition. There are 5 men and 8 women to pick from. How many ways can you pick a panel of 2 men and 2 women?
Answers
The number of ways of picking a panel of judges comprising of 2 men and 2 women is 280 ways
How to find the number of ways to pick a panel of 2 men and 2 women
Given data
number on men = 5
number of women = 8
The number of ways of picking a panel of 2 men and 2 women
= 5 combination 2 * 8 combination 2
= 5 C 2 * 8 C 2
= 5! / ( 2! ( 5 - 2 )! * 8! / ( 2! ( 8 - 2 )!
= 5! / ( 2! 3! ) * 8! / ( 2! 6! )
= 5 * 4 * 3! / ( 2! * 3! ) * 8 * 7 * 6! / ( 2! * 6! )
= 20 / 2 * 56 / 2
= 10 * 28
= 280 ways
The number of ways of picking a panel of judges comprising of 2 men and 2 women is 280 ways
Read more on combination here: https://brainly.com/question/11732255
#SPJ1
PLEASE HELP!!!!
Find the volume and surface area of the composite figure. Give four answers in terms of π.
Answer Options
V = 123π in3; S = 78π in2
V = 612π in3; S = 264π in2
V = 153π in3; S = 123π in2
V = 135π in3; S = 105π in2

Answers
Answer:
V = 135π in3; S = 105π in2
Step-by-step explanation:
entify the sampling technique. a gardener wanted to check how his tomato plants were developing. he randomly chose 2 of his 20 plants and inspected the selected plants.
Answers
The sampling technique used in this scenario is simple random sampling.
Determine the simple random sample?Simple random sampling involves randomly selecting a subset of elements from a population in such a way that every element has an equal chance of being chosen.
In this case, the gardener randomly chose 2 plants from a total of 20 plants. By randomly selecting the plants, the gardener ensured that each plant had an equal probability of being included in the sample.
Simple random sampling is a common and straightforward technique used to obtain a representative sample from a larger population. It helps minimize bias and allows for generalization of the findings from the sample to the entire population.
By inspecting the randomly selected plants, the gardener can make inferences about the development of the tomato plants as a whole, assuming that the selected plants are representative of the entire population of tomato plants.
Therefore, the gardener utilized a simple random sampling technique by randomly selecting and inspecting two out of twenty tomato plants to assess their development.
To know more about simple random sample, refer here:
https://brainly.com/question/30403914#
#SPJ4
Please help with these, in two-column chart form



Answers
The method used to prove the specified equations in the questions based on similar triangle properties are presented as follows;
3. ΔABC ~ ΔABD, indicates, AC/AB = AB/AD, therefore; AC · AD = (AB)²
4. ΔPQR ~ ΔBDR, and ΔPCQ ~ ΔABC, therefore; CP/CA = PQ/PD = PR/RD
CP/CA = PR/RD
5. ΔFXY ~ ΔFDG and ΔFXZ ~ ΔFGE, therefore; XY/DG = FY/FG = YZ/GE
XY/DG = YZ/GE
What are similar triangles?Similar triangles are triangles, A and B in which two interior angles of a triangle A are congruent to two interior angles of a triangle B, the lengths of the sides of the triangles may be different.
3. ∠1 ≅ ∠C
The reflexive property indicates that angle ∠A is congruent to itself, therefore; ∠A ≅ ∠A
Therefore, triangle ΔABC and triangle ΔABD are similar by Angle-Angle, AA similarity postulate.
Correponding parts of similar triangles are proportional, therefore; \(\frac{AC}{AB} = \frac{AB}{AD}\)
Cross multiplying, we get;
AC × AD = AB × AB = (AB)²
Therefore; AC × AD = (AB)²
4. The segment \(\overline{PQ}\) and \(\overline{AD}\) are parallel (\(\overline{PQ}\) ║ \(\overline{AD}\))
\(\overline{AB}\) ≅ \(\overline{BD}\), therefore;
\(\overline{AB}\) = \(\overline{BD}\) (definition of congruency)
∠PRQ ≅ ∠BRD (Vertical angle theorem)
∠PQR ≅ ∠DBR (Alternate interior angles theorem)
ΔPQR is similar to ΔBDR by Angle-Angle, AA similarity postulate
∠PQC ≅ ∠ABC (Same side angles theorem)
∠C ≅ ∠C (reflexive property of congruency)
Triangle ΔPCQ is aimilar to ΔABC by AA similarity postulate
CP/CA = PQ/AB
PQ/AB = PQ/BD (by substitution property)
PQ/BD = PR/RD (ratio of corresponding sides of similar triangles)
CP/CA = PQ/BD = PR/RD
Therefore; CP/CA = PR/RD
5. The segment \(\overline{XY}\) is parallel to the segment \(\overline{DE}\)
ΔFXY ~ ΔFDG
ΔFYZ ~ ΔFGE
XY/DG = FY/FG (Ratio of corresponding sides of similar triangles)
YZ/GE = FY/FG
Therefore, by the substitution property, we get;
XY/DG = YZ/GE
Learn more about similar triangles here: https://brainly.com/question/29782809
#SPJ1
Find the exact length of the third side.
63
60

Answers
Answer:
Question, are you doing pythagorean theromen?
Answer:
57
Step-by-step explanation:
By the way there is another formula so I don't know if I am 100% correct. I added 63+60. Then when you get the answer minus it by 180. I hope it helped! :)
A ___________ is used to visualize sample data graphically and to draw preliminary conclusions about the possible relationship between the variables.
Answers
A scatter plot is used to visualize sample data graphically and to draw preliminary conclusions about the possible relationship between the variables.
A scatter plot is used to visualize sample data graphically and to draw preliminary conclusions about the possible relationship between the variables. It is a type of mathematical diagram that utilizes Cartesian coordinates to display values for typically two variables for a set of data.
The data is displayed as a collection of points, each with the value of one variable determining the position on the horizontal axis and the value of the other variable determining the position on the vertical axis. Scatter plots are extremely useful when there are a large number of data points.
Summery:A scatter plot is used to visualize sample data graphically and to draw preliminary conclusions about the possible relationship between the variables.
Learn more about variablesclick here:
https://brainly.com/question/28248724
#SPJ11
PLEASE help
Allen mixes 1 cup of water that is 150°F and 1 cup of cold chicken broth that is 50°F. The end temperature of the mixture would be about___________
. Chris combines 2 cups of soup that is 50°F with 1 cup of water that is 150°F. The end temperature of the mixture would be ______
Answers
Answer:
1) 100 degrees F
2) 50 degrees F
Step-by-step explanation:
its just simple subtraction
a grocery store counts the number of customers who arrive during an hour. the average over a year is 30 customers per hour. assume the arrival of customers follows a poisson distribution. (it usually does.) find the probability that at least one customer arrives in a particular one minute period. round your answer to 3 decimals.
Answers
The probability that at least one customer arrives in a particular one-minute period is approximately 0.393, rounded to three decimal places.
To find the probability that at least one customer arrives in a particular one-minute period, we can use the Poisson distribution formula. The Poisson distribution is commonly used to model the number of events occurring within a fixed interval of time or space, given the average rate of occurrence.
In this case, we are given that the average number of customers per hour is 30. To convert this to the average number of customers per minute, we divide by 60 since there are 60 minutes in an hour. Therefore, the average number of customers per minute is 30/60 = 0.5.
The probability of no customers arriving in a particular one-minute period can be calculated using the Poisson distribution formula:
P(X = 0) = (e^(-λ) * λ^0) / 0!
Where λ is the average number of customers per minute.
Let's calculate the probability of no customers arriving in one minute:
P(X = 0) = (e^(-0.5) * 0.5^0) / 0!
= (e^(-0.5) * 1) / 1
= e^(-0.5)
Now, to find the probability that at least one customer arrives in one minute, we can subtract the probability of no customers from 1:
P(at least one customer) = 1 - P(X = 0)
= 1 - e^(-0.5)
Using a calculator, we can evaluate this expression to three decimal places:
P(at least one customer) ≈ 1 - e^(-0.5) ≈ 0.393
for such more question on probability
https://brainly.com/question/13604758
#SPJ8
If a driver brings a car traveling at 22 m/s to a full stop in 2.0 s with an acceleration of -8 m/s?, then how far did the car travel while braking?
Answers
The car traveled a distance of 30.25 meters while braking.
When a car is brought to a full stop from an initial velocity of 22 m/s with an acceleration of -8 m/s^2, we can use the laws of motion to determine the distance traveled by the car while braking.
The relevant equation to use in this case is:
\(v^2 = u^2 + 2as\)
where v is the final velocity (which is 0, since the car comes to a full stop), u is the initial velocity (which is 22 m/s), a is the acceleration (which is \(-8 m/s^2\), since the car is decelerating), and s is the distance traveled while braking.
Substituting the given values into the equation, we get:
\(0^2 = (22 m/s)^2 + 2(-8 m/s^2)s\)
Simplifying this equation, we get:
\(0 = 484 m^2/s^2 - 16s\)
\(16s = 484 m^2/s^2\)
\(s = (484 m^2/s^2) / 16s = 30.25 m\)
Therefore, the car traveled a distance of 30.25 meters while braking.
This calculation shows that the distance traveled by the car while braking depends on the initial velocity of the car and the rate at which it decelerates. In this case, the car was traveling at a high initial velocity of 22 m/s and decelerated at a rate of -8 m/s^2, which resulted in a braking distance of 30.25 meters. If the initial velocity or the deceleration rate were different, the braking distance would also be different.
Learn more about "laws of motion" :
https://brainly.com/question/26083484
#SPJ11
Select the correct answer from the drop-down menu. consider this population data set: 4, 6, 7, 11, 12, 18, 26, 23, 14, 31, 22, and 12. the values 11, 31, 22, and 12 constitute a random sample drawn from the data set. the sample mean is more than the population mean by .
Answers
The correct answer from the drop-down menu is 3.5.
What is the mean value?The mean is the average of the numbers. It is easy to calculate add up all the numbers, then divide by how many numbers in the data set.
Therefore the population mean is the sum of the 12 data set values divided by 12
4 + 6 + 7 + 11 + 12 + 18 + 26 + 23 + 14 + 31 + 22 + 12 = 186.
Therefore the population mean
= 186/12
= 15.5.
The sample mean is given by the sum of the 4 sample values divided by 4
11 + 31 + 22 + 12
Sum = 76.
Therefore the sample mean
= 76/4
= 19.
The sample mean is more than the population mean by
= 19 - 15.5
= 3.5.
To learn more about the mean visit:
https://brainly.com/question/21577204
a journalist for an automotive magazine wants to determine how the weight of a passenger vehicle, in kilograms, is related to its length, in centimeters; the maximum number of passengers; and its safety rating on a 5-point scale. what is the correct format for a multiple regression equation?
Answers
the correct format for a multiple regression equation is
ŷ= \(b_{o} + b_{1}x_{1} + b_{2}x_{2} + b_{3}x_{3} + b_{4}x_{4}\)
multiple regression: The relationship between a single dependent or criterion variable and multiple independent or predictor variables is typically explained by multiple regression. The constant term and multiple independent variables with their corresponding coefficients are used to model a dependent variable. The term "multiple regression" refers to the fact that it requires two or more predictor variables.
because, the weight of a passenger vehicle, in kilograms, is related to its length, in centimeters; and the maximum number of passengers.
thus, ŷ=\(b_{o} + b_{1}x_{1} + b_{2}x_{2} + b_{3}x_{3} + b_{4}x_{4}\) is the multiple regression equation.
know more about multiple regression here: https://brainly.com/question/28167705
#SPJ4
Calculus Consider the function 6 = x²y+yz. (a) Find its rate of change in the direction (1,2,3) at the point (1,2,-1). (b) At this same point, (1, 2,−1), in what direction does increase most rapidly? What is its rate of change in this direction?
Answers
The rate of change of the function 6 = x²y + yz in the direction (1, 2, 3) at the point (1, 2, -1) is 21. The function increases most rapidly in the direction (1, 2, 3) at the point (1, 2, -1), with a rate of change of 21.
To find the rate of change of the function in a specific direction, we can use the gradient vector. The gradient of a function represents the direction of the steepest increase, and its magnitude represents the rate of change in that direction.
The given function is 6 = x²y + yz. We need to find the rate of change in the direction (1, 2, 3) at the point (1, 2, -1).
First, we calculate the gradient of the function:
∇f = (∂f/∂x, ∂f/∂y, ∂f/∂z)
Taking partial derivatives with respect to x, y, and z, we get:
∂f/∂x = 2xy
∂f/∂y = x² + z
∂f/∂z = y
At the point (1, 2, -1), we substitute these values into the gradient:
∇f = (2(1)(2), (1)² + (-1), 2) = (4, 0, 2)
The rate of change in the direction (1, 2, 3) is given by the dot product of the gradient and the direction vector:
Rate of change = ∇f · (1, 2, 3) = (4)(1) + (0)(2) + (2)(3) = 4 + 0 + 6 = 10
Therefore, the rate of change in the direction (1, 2, 3) at the point (1, 2, -1) is 10.
Learn more about rate of change of the function:
https://brainly.com/question/29518179
#SPJ11
By what factor should -1 - 4i/ 2 + 9i be multiplied to find the quotient? Enter any complex numbers in the form a + bi
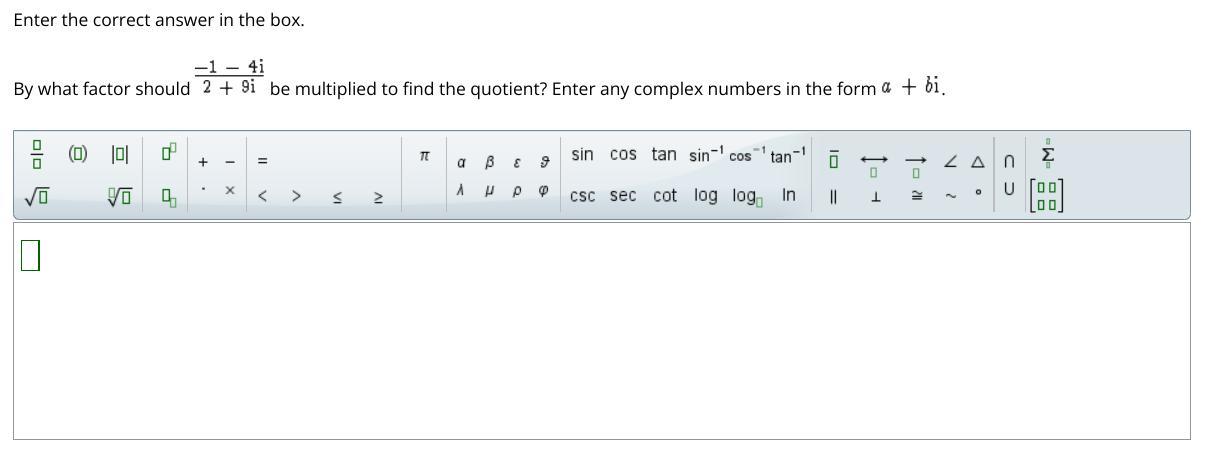
Answers
The factor by which the complex rational number be multiplied is; 2 -9i.
What value should be used to multiply to find the quotient?The expression given in the task is a fraction made up of complex numbers.
Hence in a bid to evaluate the quotient of the expression; -1 - 4i/ 2 + 9i.
The numerator and denominator must be multiplied by the conjugate of the denominator which in this case is; 2 -9i.
This is to help reduce the denominator to a real number.
Read more on division of complex numbers;
https://brainly.com/question/264450
#SPJ1
an urn contains five balls numbered 1, 2, 2, 6, and 6. how many ways can a person choose two balls at random from the urn?
Answers
There are six possible ways a person can choose two balls at random from an urn containing five balls numbered 1, 2, 2, 6, and 6.
To understand how to calculate the number of combinations, let's break it down into two parts: selecting the first ball, and then selecting the second ball. Since there are five balls in the urn, the first ball can be chosen in five possible ways. Then, when selecting the second ball, the number of possible selections is reduced to four because one ball has already been selected. This can be expressed mathematically as: n(A)=5x4.
To calculate the total number of combinations, we then multiply the two numbers: 5x4=20. This result is then divided by two because the order of selection does not matter. As a result, 20/2=10, which means that there are ten possible combinations when choosing two balls at random from the urn. In conclusion, if an urn contains five balls numbered 1, 2, 2, 6, and 6, there are six possible ways a person can choose two balls at random. This can be expressed mathematically as n(A)=6 or n(A)=5x4/2.
To know more about probability click here :
https://brainly.com/question/30034780
#SPJ11
The boiling pint of jet fuel is 329 Fahrenheit! Rounded to the nearest degree, what is the temperature in sergers Celsius? Use the formula F= 9/5 C + 32, where C represents degree Celsius and F represents degree Fahrenheit!
Answers
Answer:
165 degrees Celsius
Step-by-step explanation:
find area of a circle with a radius of 2 either enter an exact answer in terms of Pi or used to be 144
plzz aspa plzzzzzzzz
Answers
Answer:
A = 4π units²
Step-by-step explanation:
The area (A) of a circle is calculated as
A = πr² ( r is the radius ) , then
A = π × 2² = 4π units²
The concentration (in moles per liter) of oxygen in a chemical reaction is given by the function C(t) = t2 - 7t, where t is in hours. Find the rate at which the concentration of oxygen is changing after 5 hours?

Answers
Answer:
3
Step-by-step explanation:
This is a differentiation question
\( \frac{d}{dx} [t^2-7t]=2t-7 \)
C'(t) = 2t - 7
C'(5) = 2(5) - 7
C'(5) = 3
what is the result of 2.130 x 10³ - 6.6 x 10² =
Answers
Answer:
The answer you're looking for is 1470.
Step-by-step explanation:
The method I used was PEMDAS
Since there was no parenthesis, I simplified the exponents.
2.130 x 10³ - 6.6 x 10² = ?
2.130 x 1000 - 6.6 x 100 = ?
After that, I multiplied all terms next to each other.
2.130 x 1000 - 6.6 x 100 = ?
2130 - 660 = ?
The final step I did was to subtract the two final terms and ended up with 1470 as my final answer.
1470 = ?
I hope this was helpful!
Use the table to work out the values of a , b , c , and d. X y = 2 x + 1 − 3 a − 2 − 3 − 1 b 0 1 1 c 2 d a = b = c = d =
Answers
By Using the table to work out the values of a , b , c , and d. X y = 2 x + 1 − 3 a − 2 − 3 − 1 b 0 1 1 c 2 d a = b = c = d =
Therefore, The solutions are : a = -3, b = 0, c = 6, d = 9
Equation:
In mathematics, an equation is an expression that indicates equality of two expressions by connecting them with the equal sign = . The word "equation" and related words in other languages can have slightly different meanings. For example, in French an equation is defined as containing one or more variables, whereas in English a well-formed formula consisting of two expressions connected by an equal sign is an equation.
Given:
This table;
x y = 3x+3
-3 -6
-2 a
-1 b
0 3
1 c
2 d
To Find:
Values of a, b, c and d
Consider the 2nd row,
x = -2, y = a
Putting the values in the equation,
we get,
a = 3(-2) + 3
⇒ a = -3
Consider the 3rd row,
x = -1, y = b
Putting the values in the equation,
we get,
b = 3(-1) + 3
⇒ b = 0
Consider the 5th row,
x = 1, y = c
Putting the values in the equation,
c = 3(1) + 3
⇒ c = 6
Consider the 6th row,
x = 2, y = d
d = 3(2) + 3
⇒ d = 9
The final answer is,
a = -3, b = 0, c = 6, d = 9.
Learn more about solutions:
https://brainly.com/question/29263728
#SPJ4
given a function f : a → b and subsets w, x ⊆ a, then f (w ∩ x) = f (w)∩ f (x) is false in general. produce a counterexample.
Answers
Therefore, f(w ∩ x) = {0} ≠ f(w) ∩ f(x), which shows that the statement f(w ∩ x) = f(w) ∩ f(x) is false in general.
Let's consider the function f: R -> R defined by f(x) = x^2 and the subsets w = {-1, 0} and x = {0, 1} of the domain R.
f(w) = {1, 0} and f(x) = {0, 1}, so f(w) ∩ f(x) = {0}.
On the other hand, w ∩ x = {0}, and f(w ∩ x) = f({0}) = {0}.
To know more about statement,
https://brainly.com/question/31502625
#SPJ11
(2ND TIME POSTING THIS)
Solve the inequality
2/7 > b + 5/7
Answers
Answer:
b < - \(\frac{3}{7}\)
Step-by-step explanation:
Given
\(\frac{2}{7}\) > b + \(\frac{5}{7}\) ( multiply through by 7 to clear the fractions )
2 > 7b + 5 ( subtract 5 from both sides )
- 3 > 7b ( divide both sides by 7 )
- \(\frac{3}{7}\) > b , then
b < - \(\frac{3}{7}\)
(Brainliest for correct) You have decided to buy a Honda Accord LX, but you are concerned about the value of the car depreciating over time. You search the Internet and obtain the following information. The suggested retail price is $20,025. The depreciation per year is $1,385. What is the value of the car in dollars for 1 year of ownership, and how did you get that answer?
Answers
To find the value of the car after 1 year, subtract the amount it depreciates from the value of the car:
20,025 - 1,385 = 18,640
After 1 year the car is valued at $18,640
Answer:
$18640
Step-by-step explanation:
For year 1: Depreciated value is $1385.
We will minus that amount from the actual worth of car i.e. $20,025
So,
= $20,025 - $1385
= $18640
Hope this helps you.
(a^3 - 2a + 5) - (4a^3 - 5a^2 + a - 2)
Answers
Answer:
− 3 a ^3 + 5 a ^2 − 3 a + 7
Step-by-step explanation:
Apply the distributive property.
a ^3 − 2 a + 5 − ( 4 a ^3 ) − ( − 5 a ^2 ) − a − − 2
Simplify.
a ^3 − 2 a + 5 − 4 a ^3 + 5 a ^2 − a + 2
Simplify by adding terms.
Subtract 4 a ^3 from a ^3 .
− 3 a ^3 − 2 a + 5 + 5 a ^2 − a + 2
Subtract a from − 2 a .
− 3 a ^3 − 3 a + 5 + 5 a ^2 + 2
Simplify the expression.
Add 5 and 2 .
− 3 a^ 3 − 3 a + 5 a ^2 + 7
Move − 3 a .
− 3 a ^3 + 5 a ^2 − 3 a + 7
I hope this helped. I am sorry if you get this wrong.
5. (10 points) use calculus to find the absolute and local extreme values of f(x) = x 3 2 x 2/3 on the interval [−8, 8]
Answers
The absolute and local extreme values of the given function f(x) = x^3 - 2x^(2/3) on the interval [−8, 8] is 11.79.
To find the absolute extrema and local extrema of a function on a closed interval, we need to evaluate the function at the critical points and the endpoints of the interval.
First, we need to find the derivative of the function:
f'(x) = 3x^2 - (4/3)x^(-1/3)
Setting f'(x) equal to zero, we get:
3x^2 - (4/3)x^(-1/3) = 0
Multiplying both sides by 3x^(1/3), we get:
9x^(5/3) - 4 = 0
Solving for x, we get:
x = (4/9)^(3/5) ≈ 0.733
Next, we need to evaluate f(x) at the critical point and the endpoints of the interval:
f(-8) ≈ -410.38
f(8) ≈ 410.38
f(0.733) ≈ 11.79
Therefore, the absolute maximum value of f(x) on the interval [-8, 8] is approximately 410.38, and it occurs at x = 8. The absolute minimum value of f(x) on the interval is approximately -410.38, and it occurs at x = -8.
To find the local extrema, we need to evaluate the second derivative of the function:
f''(x) = 6x + (4/9)x^(-4/3)
At the critical point x = 0.733, we have:
f''(0.733) ≈ 7.28
Since f''(0.733) is positive, this means that f(x) has a local minimum at x = 0.733.
Therefore, the local minimum value of f(x) on the interval [-8, 8] is approximately 11.79, and it occurs at x = 0.733.
To learn more about absolute maximum visit: https://brainly.com/question/19921479
#SPJ11
I understand this a little but i don’t understand the angles please help me??

Answers
We can use the fact that the sum of all angles in a triangle is 180° to find the missing angles in both triangles.Therefore, the missing angles in ΔABC are ∠E = 47° and ∠F = 76°, and in ΔDEF is ∠D = 93°.
What is an angles?A geometric figure formed by two rays that share a common endpoint is termed as an angle. It is measured in degrees or radians and has different types based on its measure.
In ΔABC, we know that ∠A = 57° and that the other two angles are ∠E and ∠F. Therefore, we have:
∠A + ∠E + ∠F = 180°
57° + ∠E + ∠F = 180°
∠E + ∠F = 180° - 57°
∠E + ∠F = 123°
In triangle ΔDEF, we know that one angle is 40° and the other angle is ∠D. Therefore, we have:
∠D + 40° + ∠E = 180°
∠D + ∠E = 180° - 40°
∠D + ∠E = 140°
We now have two equations with two unknowns (∠E + ∠F = 123° and ∠D + ∠E = 140°). Solving the system of equations simultaneously gives us:
∠E = 47°
∠F = 76°
∠D = 93°
To know more about triangle visit:
https://brainly.com/question/2773823
#SPJ1
Students at a school went on a trip. The given equation models the total cost of the trip, where x is the number of students who went on the trip.
Answers
Answer:
50 students
Step-by-step explanation:
Students at a school went on a trip. The given equation models the total cost of the trip, where x is the number of students who went on the trip.
18x = 900
How many students went on the trip?
Given equation:
18x = 900
Where,
x = number of students who went on the trip
Number of students who went for the trip
18x = 900
x = 900/18
x = 50 students
Therefore, 50 students went for the trip
how to find slope of tangent line using implicit differentiation
Answers
Solve for dy/dx: dy/dx = (-2x) / (2y) = -x / y which gives the slope of tangent line using implicit differentiation
To find the slope of a tangent line using implicit differentiation, follow these steps:
1. Start with the given equation that represents the relationship between x and y in the form of an equation involving both variables, for example: F(x, y) = 0.
2. Differentiate both sides of the equation with respect to x using the chain rule whenever necessary. Treat y as a function of x and apply the derivative rules accordingly.
3. After differentiating, have a resulting equation involving both x, y, and their derivatives (dy/dx). Rearrange the equation if necessary to isolate dy/dx on one side.
4. Solve for dy/dx to find the derivative of y with respect to x. This will give the slope of the tangent line at any given point on the curve defined by the implicit equation.
Note: The resulting expression for dy/dx may involve both x and y variables. To find the slope of the tangent line at a specific point, substitute the coordinates of that point into the expression for dy/dx.
Here's an example to illustrate the process:
Given the implicit equation: \(x^2 + y^2 = 25\)
1. Start with the equation: \(x^2 + y^2 = 25.\)
2. Differentiate both sides with respect to x:
2x + 2y * (dy/dx) = 0
3. Rearrange the equation to isolate dy/dx:
2y * (dy/dx) = -2x
4. Solve for dy/dx:
dy/dx = (-2x) / (2y)
= -x / y
Now, have the expression for the slope of the tangent line in terms of x and y. To find the slope at a specific point, substitute the coordinates of that point into the expression.
To learn more about implicit differentiation
https://brainly.com/question/11887805
#SPJ11
Suppose that the heights of males in the U.S. follow a normal distribution with a mean of 70 inches and a standard deviation of 4 inches. If we took a random sample of 54 U.S. males, what is the probability that (a) The sample mean height will be less than 69 inches
Answers
The probability that the sample mean height will be less than 69 inches is 0.966 or 96.6%.
What is normal distribution?The normal distribution, like any other probability distribution, defines how well the values of a statistic are distributed. Because it accurately captures the range of values for many natural occurrences, it is the most significant probability distribution in statistics.
The formula for normal distribution is;
\(Z=\frac{\bar{X}-\mu}{\left(\frac{\sigma}{\sqrt{n}}\right)}\)
Where, X is the sample average( = 69).
μ is the mean (= 70).
σ is the standard distribution ( = 4)
n is the sample size (= 54).
Substituting above values in the formula;
\(z=\frac{69-70}{\left(\frac{4}{\sqrt{54}}\right)}\)
z = -1.83
So the likelihood that it sample mean is less than 69 would be the probability of Z will be greater than -1.83 This is determined using the Z-table:
P( < 69) = P(Z < -1.83) = 0.966
Therefore, the probability for getting the sample mean height will be less than 69 inches is 0.966 or 96%.
To know more about the normal distribution, here
https://brainly.com/question/6476990
#SPJ4
options of Answer
A) 10 bags of chips and 2 jars of salsa
B) 20 bags of chips and 2 jars of salsa
C) 14 bags of chips and 5 jars of salsa
D) 18 bags of chips and 6 jars of salsa

Answers
Answer:
D) 18 bags of chips and 6 jars of salsa
Step-by-step explanation:
Given : The networking organization you joined is throwing a party. You are in charge of buying the chips, which cost $2.50 per bag and salsa, which costs $4 per jar. The chips & salsa budget you are given totals $60.
Inequality: \(2.5x+4y\) ≤ \(60\)
Solution :
x represents chips
y represents salsa
Option a: 10 bags of chips and 2 jars of salsa
so, x = 10 and y =2
Putting values in inequality
\(2.5(10)+4(2)\) ≤\(60\)
\(25+8\) ≤\(60\)
\(33\)≤\(60\)
Hence it is correct.
Option c : 14 bags of chips and 5 jars of salsa
so, x = 14 and y =5
Putting values in inequality
\(2.5(10)+4(2)\)≤\(60\)
\(50+8\)≤\(60\)
\(58\)≤\(60\)
Hence it is correct.
Option c : 14 bags of chips and 5 jars of salsa
so, x = 14 and y =5
Putting values in inequality
\(2.5(14)+4(5)\)≤\(60\)
\(35+20\)≤\(60\)
\(55\)≤\(60\)
Hence it is correct.
Option d :18 bags of chips and 6 jars of salsa
so, x = 18 and y =6
Putting values in inequality
\(2.5(18)+4(6)\)≤\(60\)
\(45+24\)≤\(60\)
\(69\geq 60\)
Hence it is not correct since it violates the inequality