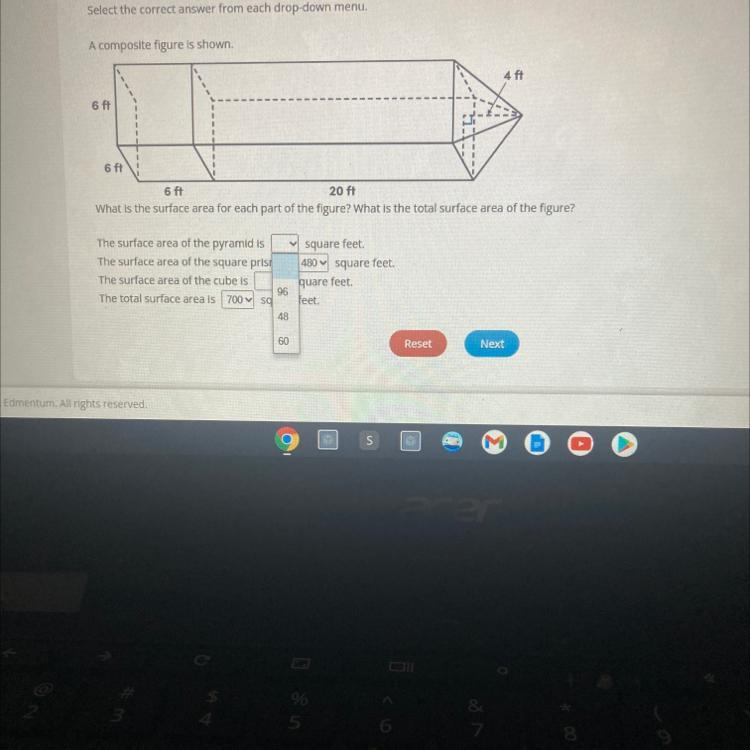
Answers
Given:
• Length of base(cube) = 6 ft
,• Height of square prism = 20 ft
,• Height of pyramid =4 ft
Since it is a composite figure, the surface of some sides will not be included in the surface area.
Let's solve for the following:
• (a). The surface area of the pyramid.
To find the surface area of the pyramid, apply the formula:
\(SA=A+\frac{1}{2}ps\)Where:
A is the area of the base
p is the perimeter of the base
s is the slant height.
To find the slant height, apply Pythagorean theorem:
\(\begin{gathered} s=\sqrt{(4)^2+(\frac{6}{2})^2} \\ \\ s=\sqrt{16+9}=\sqrt{25}=5\text{ ft} \end{gathered}\)We have:
\(\begin{gathered} SA=(6*6)+\frac{1}{2}(6*4)*5 \\ \\ SA=36+\frac{1}{2}(24)*5 \\ \\ SA=36+60 \\ \\ SA=96\text{ ft}^2 \end{gathered}\)The surface area of the pyramid is 96 ft².
• (b). Surface area of the square prism.
Apply the formula:
\(\begin{gathered} SA=3ah \\ \\ SA=4(6)(20) \\ \\ SA=480\text{ ft}^2 \end{gathered}\)The surface area of the square prism is 480 ft².
• (c). Surface area of the cube.
To find the surface area of the cube, we have:
\(\begin{gathered} SA=6a^2 \\ \\ SA=6(6)^2 \\ \\ SA=216\text{ ft}^2 \end{gathered}\)The surface area of the cube is 216 ft²
The total surface area will be:
T = Surface area of pyramid + surface area of prism + surface area of cube - area of base
T = 96 + 480 + 216 - 36
T = 756 ft²
ANSWER:
Surface area of the pyramid is 96 ft².
Surface area of the square prism is 480 ft².
Surface area of the cube is 216 ft²
Total surface area is 756 ft²
Related Questions
The line plot displays the number of roses purchased per day at a grocery store.
A horizontal line starting at 0 with tick marks every one unit up to 10. The line is labeled Number of Rose Bouquets, and the graph is titled Roses Purchased Per Day. There is one dot above 10. There are two dots above 1 and 4. There are three dots above 2 and 5. There are 4 dots above 3.
Which of the following is the best measure of variability for the data, and what is its value?
The IQR is the best measure of variability, and it equals 3.
The IQR is the best measure of variability, and it equals 9.
The range is the best measure of variability, and it equals 3.
The range is the best measure of variability, and it equals 9.
Answers
The range is the best measure of variability for this data, and its value is 4.
Which of the following is the best measure of variability for the data, and what is its value?The line plot displays the number of roses purchased per day at a grocery store, with the data values ranging from 0 to 4 (since there are no dots above 4).
The best measure of variability for this data is the range, which is the difference between the maximum and minimum values in the data set. In this case, the minimum value is 0 and the maximum value is 4, so the range is:
Range = Maximum value - Minimum value = 4 - 0 = 4
Therefore, the range is the best measure of variability for this data, and its value is 4.
to know more about range
brainly.com/question/29452843
#SPJ1
Evaluate the following, using the distributive property. (i) – 39 × 99
(ii) (– 85) × 43 + 43 × ( – 15)
(iii) 53 × ( – 9) – ( – 109) × 53
(iv) 68 × (–17) + ( –68) × 3
(v) 26 x (-48) + (-48) x 36
(vi) (-41) x 102
(vii)(-57) x (-19) + 5
Answers
Answer:
(i) - 33 × 99
= - 3267
(iii) 53 × ( - 9) - ( - 109) × 53
= - 477 + 109 × 53
= - 477 + 5777
= + 5300
(ii) (-85) × 43 + 43 × ( - 15)
= - 3655 + 43 - 645
= - 3655 - 645 + 43
= - 4300 + 43
= - 4257
At a sale, shirts were sold for $20 each. This price was 80% of their original price. What was the original price?
(SHOW THE WORK)
Answers
Answer:
100%hajsmsmwkwkkqjwjnwnw
Linear sequence of 35/100,5/10,65/100
Answers
The linear rule for the sequence is f(n) = 7/20 + 3/20(n - 1)
Finding the linear rule for the sequenceFrom the question, we have the following parameters that can be used in our computation:
35/100,5/10,65/100
In the above sequence, we can see that 15/100 is added to the previous term to get the new term
This means that
First term, a = 35/100
Common difference, d = 15/100
The nth term is then represented as
f(n) = a + (n - 1) * d
Substitute the known values in the above equation, so, we have the following representation
f(n) = 35/100 + 15/100(n - 1)
So, we have
f(n) = 7/20 + 3/20(n - 1)
Hence, the explicit rule is f(n) = 7/20 + 3/20(n - 1)
Read more about sequence at
brainly.com/question/30499691
#SPJ1
A movie theater can seat a maximum of 25 people. Let p represent the total number of people. Which inequality represents p, the number of people the theater can seat?
Answers
The inequality that represents p, the number of people the theater can seat is p ≤ 25
Which inequality represents p, the number of people the theater can seat?From the question, we have the following parameters that can be used in our computation:
A movie theater can seat a maximum of 25 people
This means that
Maximum = 25 people
In other words, the movie theatre can allow 25 or less people to attend a movie
In inequality, 25 or less means less than or equal to 25
When represented as an inequality expression, we have
≤ 25
Using the variable p, we have
p ≤ 25
Hence, the inequality is p ≤ 25
Read more about inequality at
https://brainly.com/question/30390162
#SPJ1
The product of 4 and the difference of a number and 7.
Answers
Answer:
simplified: 4x−28
Step-by-step explanation:
The product of 4 and the difference of a number and 7 can be written as 4(x-7) where x is the number you are looking for.
there are 60 students at a college..20 students study both French and Spanish, a total of 43 students study Spanish....complete the Venn diagram for this information
Answers
Answer:
A: 13
B: 20
C: 23
Don't study: 4 students
A store owner uses pieces of tape to paint a window advertisement. The letters are slanted at an 80 degree angle. What is the measure of angle 1?
Answers
Answer:
∠1 is 180° − 80° = 100°.
Step-by-step explanation:
Using the corresponding angles, the 80° angle is congruent to the angle that is supplementary to ∠1, as shown. The measure of ∠1 is 180° − 80° = 100°.
The measure of ∠b comes to be 100°.
As we know,
In window advertisement,
∠b and 80° are supplementary angles to each other.
What are the supplementary angles?When the sum of Two angles is 180°, each angle is said to be the supplement of the other angle.
As ∠b +80° =180°
∠b = 180°-80°
∠b = 100°.
Therefore, The measure of ∠b comes to be 100°.
To get more about supplementary angles visit:
https://brainly.com/question/12919120
Kristen has 8 gallons of water. Chris has 28 quarts of water. How many more pints of water does Kristen have than Chris?
Answers
Kristen have 8 cups more than Chris.
We will use unitary method for solving a problem by the first value of a single unit and then finding the value by multiplying the single value.
Given that Kristen has 8 gallons of water. Chris has 28 quarts of water.
We need to convert gallons and quarts to cups and subtract the values
1 gallon = 16 cups
7 gallons = 7 x 16 = 112 cups
1 quart = 4 cups
Therefore,
26 quarts = 26 x 4 = 104 cups
112 - 104 = 8 cups
Learn more about the unitary method, please visit the link given below;
https://brainly.com/question/23423168
#SPJ7
Using 50 random numbers given below, compute the mean and standard deviation. 0.937776 0.270012 0.243785 0.590701 0.824982 0.131805 0.879337 0.741998 0.254683 0.080259 0.419321 0.928220 0.958430 0.980182 0.263900 0.063119 0.762096 0.485612 0.662900 0.362242 0.724796 0.307736 0.305021 0.417052 0.054337 0.323357 0.069662 0.843387 0.353107 0.074262 0.735596 0.175095 0.390508 0.668932 0.029861 0.205228 0.387740 0.962169 0.646565 0.423914 0.754782 0.156719 0.773113 0.546335 0.323573 0.649740 0.214082 0.382383 0.383982 0.030539 Mean = (to 6 decimals) Standard deviation = (to 6 decimals)
Answers
The mean is 0.477514 (rounded to 6 decimal places).
The standard deviation is 0.288919 (rounded to 6 decimal places).
How to Solve the Problem?To calculate the mean and standard deviation, we will use the following formulas:
Mean = (sum of all values) / (number of values)
Standard deviation = sqrt[(sum of (value - mean)^2) / (number of values)]
Using these formulas, we can calculate the mean and standard deviation for the given set of random numbers:
Mean = (0.937776 + 0.270012 + 0.243785 + 0.590701 + 0.824982 + 0.131805 + 0.879337 + 0.741998 + 0.254683 + 0.080259 + 0.419321 + 0.928220 + 0.958430 + 0.980182 + 0.263900 + 0.063119 + 0.762096 + 0.485612 + 0.662900 + 0.362242 + 0.724796 + 0.307736 + 0.305021 + 0.417052 + 0.054337 + 0.323357 + 0.069662 + 0.843387 + 0.353107 + 0.074262 + 0.735596 + 0.175095 + 0.390508 + 0.668932 + 0.029861 + 0.205228 + 0.387740 + 0.962169 + 0.646565 + 0.423914 + 0.754782 + 0.156719 + 0.773113 + 0.546335 + 0.323573 + 0.649740 + 0.214082 + 0.382383 + 0.383982 + 0.030539) / 50 = 0.477514
Therefore, the mean is 0.477514 (rounded to 6 decimal places).
Now we will calculate the standard deviation:
Standard deviation = sqrt[((0.937776 - 0.477514)^2 + (0.270012 - 0.477514)^2 + (0.243785 - 0.477514)^2 + ... + (0.382383 - 0.477514)^2 + (0.383982 - 0.477514)^2 + (0.030539 - 0.477514)^2) / 50] = 0.288919
Therefore, the standard deviation is 0.288919 (rounded to 6 decimal places).
Learn more about mean here: https://brainly.com/question/20118982
#SPJ1
Consider the following figure.
(Note that the figure is not drawn to scale.)
20°
L
47°
89°
Order the side lengths IK, KL, IJ, IL, and LJ from least to greatest.
Answers
The side lengths from least to greatest as follows:
IK < KL < IJ < IL < LJ
To order the side lengths IK, KL, IJ, IL, and LJ from least to greatest, we can analyze the given figure.
Since the figure is not drawn to scale, we cannot determine the exact lengths of the sides. However, we can make some observations based on the given angles.
Let's analyze the angles:
Angle L: Since angle L is marked as 47°, we know that side KL is the shortest side, as it is opposite to the smallest angle in a triangle.
Angle I: Since angle I is marked as 20°, we can infer that side IJ is longer than side IK, as it is opposite to a larger angle.
Angle LJ: Since angle LJ is marked as 89°, we can conclude that side LJ is the longest side, as it is opposite to the largest angle in the triangle.
Based on these observations, we can order the side lengths from least to greatest as follows:
IK < KL < IJ < IL < LJ
For such more questions on Side Length Order Analysis
https://brainly.com/question/17137941
#SPJ8
Find the equation to the line

Answers
The equation of the line is y = 2/3x + 1
How to determine the equation of the line?The graph represents the given parameter
From the graph, we have the following points that can be used in our computation:
(x, y) = (0, 1) and (3, 3)
The equation of the line is then calculated using the following equation
y = (y₂ - y₁)/(x₂ - x₁) * (x - x₁) + y₁
Where
(x, y) = (0, 1) and (3, 3)
Substitute the known values in the above equation, so, we have the following representation
y = (3 - 1)/(3 - 0) * (x - 0) + 1
Evaluate
y = 2/3 (x - 0) + 1
So, we have
y = 2/3x + 1
Hence, the line equation is y = 2/3x + 1
Read more about linear equations at
https://brainly.com/question/2030026
#SPJ1
(1 point) Some shrubs have the useful ability to resprout from their roots after their tops are destroyed. Fire is a particular threat to shrubs in dry climates, as it can injure the roots as well as destroy the aboveground material. One study of resprouting took place in a dry area of Mexico. The investigation clipped the tops of samples of several species of shrubs. In some cases, they also applied a propane torch to the stumps to simulate a fire. Of 16 specimens of a particular species, 7 resprout after fire. Estimate with 99% confidence the proportion of all shrubs of this species that will resprout after fire.
Answers
Answer:
The answer is "\(0.45 \pm 0.18204\)"
Step-by-step explanation:
For the +4 sample proportion\(= \frac{(7+2)}{(16+4)} = \frac{9}{20} = 0.45\)
Sample percentage measurements estimated stdev
\(= \sqrt{\frac{[(0.45)(1-0.45)]}{[(16+4)]}}\\\\ = \sqrt{\frac{[(0.45)(0.55)]}{[(20)]}}\\\\ = \sqrt{\frac{0.2475}{20}}\\\\= \sqrt{0.012375}\\\\=0.111\)
Calculating the critical z for a=0.1, two-tailed = 1.64
Calculating the confidence interval:
\(= 0.45 \pm 0.111 \times 1.64 \\\\= 0.45 \pm 0.18204\)
Can I please get help with B
Answers
Answer:
sure just bring the question and it will be answered
quadrilateral a'b'c'd' is the image of quadrilateral abcd under a dilation with a scale factor of 1/3?

Answers
Answer:
6
Step-by-step explanation:
The required measure of the line CD is 6 units, as of the given conditions.
Given that
Quadrilateral a'b'c'd' is the image of quadrilateral abcd under a dilation with a scale factor of 1/3.
The scale factor is defined as the ratio of the modified change in length to the original length.
here,
Given scale factor = 1/3
Now,
C'D'/ CD = 1/3
CD = 3 C'D'
CD = 3 × 2
CD = 6 units
Thus, the required measure of the line CD is 6 units, as of the given conditions.
Learn more about Scale factors here:
https://brainly.com/question/22312172
#SPJ5
Need help with top problem. Maybe bottom too

Answers
1) The area of a circle circumscribed about a square is 307.7 cm².
2.a.) The angle ACB is 39 degrees.°.
2b.) The value of x is 5.42.
How to determine the area of a circle?We shall find the radius to determine the area of a circle.
First, find the side length of the square:
Since the perimeter of the square = 56 cm, then, each side of the square is 56 cm / 4 = 14 cm.
Next, find the diagonal of the square, using the Pythagorean theorem:
Diagonal = the diameter of the circumscribed circle.
Diagonal² = side length² + side length²
= 14 cm² + 14 cm²
= 196 cm² + 196 cm²
= 392 cm²
Take the square root of both sides:
Diagonal = √392 cm ≈ 19.80 cm (rounded to two decimal places)
Then, the radius of the circle which is half the diagonal:
Radius = Diagonal / 2 ≈ 19.80 cm / 2 ≈ 9.90 cm (rounded to two decimal places)
Finally, compute the area of the circle using the formula:
Area = π * Radius²
Area = 3.14 * (9.90 cm)²
Area ≈ 307.7 cm² (rounded to two decimal places)
Therefore, the area of the circle that is circumscribed about a square with a perimeter of 56 cm is 307.7 cm².
2. a) We use the property of angles in a circle to solve for angle ACB: an angle inscribed in a circle is half the measure of its intercepted arc.
Given that arc AB has a measure of 78°, we can find angle ACB as follows:
Angle ACB = 1/2 * arc AB
= 1/2 * 78°
= 39°
Therefore, the angle ACB is 39 degrees.
2b.) To solve for the value of x, we use the information that the angle ADB = (3x - 12)⁴.
Given that angle ADB is (3x - 12)⁴, we can equate it to the measure of the intercepted arc AB, which is 78°:
(3x - 12)⁴ = 78
Solve the equation for x, by taking the fourth root of both sides:
∛∛((3x - 12)⁴) = ∛∛78
Simplify,
3x - 12 = ∛(78)
Isolate x by adding 12 to both sides:
3x - 12 + 12 = ∛(78) + 12
3x = ∛(78) + 12
Finally, divide both sides by 3:
x = (∛(78) + 12) / 3
x = (4.27 +12) / 3
x = 5.42
So, x is 5.42
Therefore,
1) The area of the circle is 154 cm².
2a.) Angle ACB is equal to 102°.
2b.) The value of x is 5.42
Learn more about the area of a circle at brainly.com/question/12374325
#SPJ1
Karen finished watching a movie at 1:10 pm. The movie lasted 1 hour and 38 minutes. What is the time that karen started watching the movie
Answers
Answer:
11:32:00 AM
Step-by-step explanation:
(10 Points) Tanya is visiting New Orleans, and she wants to bring back T-shirts for all her friends. She’s
found T-shirts she likes for $5, $10, and $15. She has budgeted $40 for the gifts. make a systematic list
to answer the following questions.
(i) List how many ways she can spend exactly $30 if she is determined to buy one or more than one
$15 T-shirts?
(ii) List how many ways she can spend exactly $25.
Help its due in 1 hour plzzz!!!!!!! can you show your work to
Answers
Answer:
ok.
1. Tanya spends exactly $30.
She can spend $15.00 each for 2 t shirts and spend $30.00
15 x 2 = 30
She can buy one $15.00 t shirt, one $10.00 t shirt and one $5.00 t shirt for exactly $30.00.
15 + 10 + 5 = 30
She can buy one $15.00 t shirt, and three $5.00 t shirts for exactly $30.00
15 + 5 + 5 +5 = 30
2. To spend exactly $25.00, Tanya can spend it :
5 of the $5.00 t shirts
5 x 5 = 25
2 of the $10 t shirts and one of the $5 t shirts
10 + 10 + 5 = 25
1 of the $15 t shirts and one of the $10 t shirts
15 + 10 = 25
1 of the $15 t shirts and 2 of the $5 t shirts
15 + 5 + 5 = 25
late the sentence into an equation.
Three less than the product of 2 and a number is 4 .
Use the variable x for the unknown number.
Answers
The expression of the given statement is 2y - 3 = -1
What is Expression?Expressions are mathematical statements that comprise either numbers, variables, or both and at least two terms associated by an operator. The operations of mathematics include multiplication, division, addition, and subtraction.
A phrase is considered a mathematical expression if it contains at least two numbers or variables and one or more mathematical operations. Let's look at how expressions are written.
The expression of the given statement is 2y - 3 = 4.
Here, let the unknown number = y
Now, product of y and 2 = 2 times y = 2y
Also, three less than the product = Product - 3
So, three less than the product of 3 and y = 2 y - 3
Now, this above expression is equivalent to -1.
⇒2 y - 3 = -1
Hence the expression of the given statement is 2y - 3 = -1
To know more about Expression, visit:
https://brainly.com/question/1859113
#SPJ1
The sentence "Three less than the product of 2 and a number is 4" can be translated into the equation: 2x - 3 = 4
What is an equation?A mathematical statement that demonstrates the equivalence of two expressions is known as an equation.
It has two sides that are divided by the equals sign (=).
Variables, constants, coefficients, operators, and functions can all be used in the expressions on either side of the equation.
Here, x represents the unknown number that we are trying to solve for. The expression "the product of 2 and a number" is represented by 2x, and "three less than" is represented by the subtraction of 3 from that product. This expression is set equal to 4, which is the result given in the original sentence.
To know more about expressions visit:
https://brainly.com/question/19131200
#SPJ1
Find the area of an equilateral triangle with apothem length 4 cm.
If necessary, write your answer in simplified radical form.
Answers
Step-by-step explanation:
Hey there!
According to the question;
Side (a) = 4cm
To find : area
Now;
\(area = \frac{ \sqrt{3} }{4} {(a)}^{2} \)
\(or \: area = \frac{ \sqrt{3} }{4} ( {4)}^{2} \)
\(area \: = 4 \sqrt{3} \)
Therefore, area of triangle is 6.92 cm² or 4√(3) cm².
Hope it helps!
The table shows Mitch’s record for the last thirty par-3 holes he has played.
Based on this record, what is the probability that Mitch will score a 2 or 3 on the next par-3 hole?
a. 7/9
b. 3/5
c. 3/10
d. 9/50

Answers
Answer:c. 3/10
Step-by-step explanation:
Explain how the distributive property helps us multiply the following polynomials and why and how the final products differ:(a + b)^2,(a – b)^2,(a - b)(a + b)
Answers
Answer:
because you have to distrubute the 2 to the letters inside the () or else youll get a diff answer thats wrong
Step-by-step explanation:
Mary invested $200 for 3 years at 5% per annum. John invested $300 at the same rate. If they both received the same amount of interest how much did john invest???
Answers
Answer:
Step-by-step explanation:
An arrow is shot from 3 ft above the top of a hill with a vertical upward velocity of 108 ft/s. If it strikes the plain below after 9.5 s, how high is the hill?
If the arrow is launched at t0, then write an equation describing velocity as a function of time?
Answers
The height of the hill is approximately 25.73 ft. Where v0 is the initial velocity (108 ft/s), g is the acceleration due to gravity \((-32.2 ft/s^2)\),
To find the height of the hill, we can use the formula for the vertical position of an object under constant acceleration:
h = h0 + v0t + 1/2at^2
where h is the final height, h0 is the initial height, v0 is the initial velocity, t is the time, and a is the acceleration due to gravity (-32.2 ft/s^2).
In this case, we are given that the initial height h0 is 3 ft, the initial velocity v0 is 108 ft/s, and the time t is 9.5 s. We want to find the height of the hill, which we can denote as h_hill. The final height is the height of the plain, which we can denote as h_plain and assume is zero.
At the highest point of its trajectory, the arrow will have zero vertical velocity, since it will have stopped rising and just started to fall. So we can set the velocity to zero and solve for the time it takes for that to occur. Using the formula for velocity under constant acceleration:
v = v0 + at
we can solve for t when v = 0, h0 = 3 ft, v0 = 108 ft/s, and a = -32.2 ft/s^2:
0 = 108 - 32.2t
t = 108/32.2 ≈ 3.35 s
Thus, it takes the arrow approximately 3.35 s to reach the top of its trajectory.
Using the formula for the height of an object at a given time, we can find the height of the hill by subtracting the height of the arrow at the top of its trajectory from the initial height:
h_hill = h0 + v0t + 1/2at^2 - h_top
where h_top is the height of the arrow at the top of its trajectory. We can find h_top using the formula for the height of an object at the maximum height of its trajectory:
h_top = h0 + v0^2/2a
Plugging in the given values, we get:
h_top = 3 + (108^2)/(2*(-32.2)) ≈ 196.78 ft
Plugging this into the first equation, we get:
h_hill = 3 + 108(3.35) + 1/2(-32.2)(3.35)^2 - 196.78
h_hill ≈ 25.73 ft
If the arrow is launched at t0, the equation describing velocity as a function of time would be:
v(t) = v0 - gt
For such more questions on velocity
https://brainly.com/question/25749514
#SPJ8
ABCD is an area in the shape of rhombus in which
120°. Find the measure of
If u answer will mark brainlyest and will give 40 points

Answers
Answer:
The measure of <CDO and <DCo are 60° and 30°.
Step-by-step explanation:
∠CDO = 1/2 ∠CDA
= 1/2 (120)° = 60°
∠ADC + ∠DCB = 180°
120° + ∠DCB = 180°
⇒ ∠DCB = 180° – 120° = 60°
∠DCO = 1/2 ∠DCB
= 1/2 (60°) = 30°
I hope this helps, have a good day! :D
So,
∠CDO = 1/2 ∠CDA
= 1/2 (120)° = 60°
∠ADC + ∠DCB = 180°
120° + ∠DCB = 180°
⇒ ∠DCB = 180° – 120° = 60°
∠DCO = 1/2 ∠DCB
= 1/2 (60°) = 30°
im doing decimals greatest to least and i need help with number 12 and 13
Answers
(I know there isnt any real problem here to solve, but heres a tip on how to solve greatest to least with decimal problems)
1. Just because a number looks big, doesn't mean it is big
Example: 1.00000000000001 < 1.1
just look at the numbers ^ and dont just hastily read it over assuming that 1.1 is smaller because it "has less digits"
2. Negative numbers are... opposite. and they are less than positive numbers
-3.4 > -4.1
Why is this? Well, if you look on a line, with the point 0 in the middle, you can see that -3.4 is not as far away from 0 as -4.1 is. So the idea is to apply opposite logic for negative numbers
I hope these tips helped!! :D
Answer:
12) 6.32, 6.318, 6.23, 6.108
13) 1.345, .654, .645, .456
Step-by-step explanation:
What is most likely the line of best fit for this scatter plot?
2234H205642
18
16
14
12
10
0123456789 10 12 14
O Line A
Line B
O Line C
O Line D
Answers
The most likely the line of best fit for this scatter plot is line C.
What is scatterplot?It should be noted that a scatterplot simply means a graph that shows the relationship between the variables in the data set.
In this case, the most likely the line of best fit for this scatter plot is line C. The dependent variable is illustrated in the x axis and the dependent variable is illustrated on the y axis.
Learn more about scatterplot on:
brainly.com/question/6592115
#SPJ1

Please ANSWER!!!!!!!

Answers
Answer:
See explanation
Step-by-step explanation:
It appears that the second graph is better since it seems to be rather consistent. The graph of the first one seems out of place. Therefore it seems to be confusing and could be misleading.
Suppose the function h(x) = 2x - 9 is translated up 5 units to become a new function,
Xx). What's the equation of the new function?
A) x) = 7x-4
B)(x) = 2x - 14
C)(x) = 7x-9
D) (x)=2x-4
Answers
According to the given data the equation of the new function is (D) f(x) = 2x - 4.
What is meant by equation?An equation is a mathematical statement that indicates that two expressions are equal. It contains an equals sign "=" and may involve variables, constants, and mathematical operations such as addition, subtraction, multiplication, division, exponentiation, etc.
According to the given information:If we translate the function h(x) = 2x - 9 up by 5 units, the new function f(x) will have the form:
f(x) = h(x) + 5
Substituting the definition of h(x) into this equation, we get:
f(x) = 2x - 9 + 5
Simplifying, we have:
f(x) = 2x - 4
Therefore, the equation of the new function is (D) f(x) = 2x - 4.
To know more about equations visit:-
https://brainly.com/question/22964920
#SPJ1
Q1. An industry analyst wants to compare the average salaries of two firms, both to each other and to the industry. Firm A's average salary is 93% of the industry average, Firm B's average salary is $58,000, and the industry average salary is 96% of Firm B's average salary. a. Determine the industry average salary. b. Determine Firm A's average salary. c. Express Firm B's average salary as a percentage of Firm A's average salary. Round the percentage to two decimals.
Answers
a.The Industry Average Salary is $55,680. b.The Firm A's Average Salary is $51,718.40 .c. Firm B's average salary is approximately 112.27% of Firm A's average salary.
a. To determine the industry average salary, we can use the information that the industry average salary is 96% of Firm B's average salary. Firm B's average salary is $58,000. Therefore, we can calculate the industry average salary as follows:
Industry Average Salary = 96% of Firm B's Average Salary
= 0.96 * $58,000
= $55,680
b. Firm A's average salary is stated as 93% of the industry average salary. To calculate Firm A's average salary, we can multiply the industry average salary by 93%:
Firm A's Average Salary = 93% of Industry Average Salary
= 0.93 * $55,680
= $51,718.40
c. To express Firm B's average salary as a percentage of Firm A's average salary, we can divide Firm B's average salary by Firm A's average salary and multiply by 100:
Percentage = (Firm B's Average Salary / Firm A's Average Salary) * 100
= ($58,000 / $51,718.40) * 100
≈ 112.27%
For more such questions on Industry Average Salary
https://brainly.com/question/28947236
#SPJ8