What is a Rectangular Coordinate System
Answers
Answer:
Cartesian coordinate system in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length.
Related Questions
Let f(x, y) = ln(1 + 2x + y). Consider the graph of z = f(x,y) in the xyz- space. (a) Find the equation of the tangent plane of this graph at the point (0,0,0). (b) Estimate the value of f(-0.3, 0.1) using the linear approximation at the point (0,0).
Answers
(a) The equation of the tangent plane of the graph of the function z = f(x,y) at the point (0,0,0) is given by z = f(0,0) + fx(0,0)(x-0) + fy(0,0)(y-0).
We have f(0,0) = ln(1 + 2(0) + 0) = ln(1) = 0, fx(x,y) = 2/(1+2x+y)² and fy(x,y) = 1/(1+2x+y)². Thus the equation of the tangent plane of the graph at (0,0,0) is z = 0 + 2(x-0) + 1(y-0) = 2x + y.
(b) The linear approximation of the function f(x,y) = ln(1 + 2x + y) at the point (0,0) is given by L(x,y) = f(0,0) + fx(0,0)(x-0) + fy(0,0)(y-0). We have f(0,0) = 0, fx(x,y) = 2/(1+2x+y)² and fy(x,y) = 1/(1+2x+y)².
Therefore, L(x,y) = 0 + 2x + y = 2x + y. We want to estimate the value of f(-0.3,0.1) using this linear approximation at (0,0). Therefore, x = -0.3 - 0 = -0.3 and y = 0.1 - 0 = 0.1. Then we have L(-0.3,0.1) = 2(-0.3) + 0.1 = -0.5. Thus, we can estimate that f(-0.3,0.1) ≈ -0.5.
The linear approximation is an important concept in Calculus. It is a way of approximating the value of a function at a point by using the values of the function and its derivatives at a nearby point. It is useful when we want to estimate the value of a function at a point that is close to a point where we know the value of the function and its derivatives.
The linear approximation is given by L(x, y) = f(a, b) + fx(a, b)(x-a) + fy(a, b)(y-b), where a and b are the coordinates of the point where we know the value of the function and its derivatives.
To know more about tangent plane refer here:
https://brainly.com/question/6256325#
SPJ11
4. Consider the ground state of the Harmonic Oscillator with the potential in the k standard form V = x² so the potential well is centered at x = 0. 2 (a) Evaluate the values of (x²) and σ₂ = √
Answers
(a) To evaluate (x^2) for the ground state of the Harmonic Oscillator, we need to integrate x^2 multiplied by the square of the absolute value of the wavefunction ψ0(x).
(b) The expectation value of p^2 for the ground state of the Harmonic Oscillator is simply the eigenvalue corresponding to the momentum operator squared.
(c) By calculating the uncertainties in position (Δx) and momentum (Δp) for the ground state, we can verify that their product satisfies Heisenberg's uncertainty principle, Δx · Δp ≥ ħ/2.
(a) In the ground state of the Harmonic Oscillator, the wavefunction is given by \(\psi_0(x) = \frac{1}{\sqrt{\sigma}}e^{-\frac{x^2}{2\sigma^2}}\), where \(\sigma\) is the standard deviation.
To evaluate \((x^2)\), we need to find the expectation value of \(x^2\) with respect to the wavefunction \(\psi_0(x)\). Using the formula for the expectation value, we have:
\((x^2) = \int_{-\infty}^{\infty} x^2 \left|\psi_0(x)\right|^2 dx\)
Substituting the given wavefunction, we have:
\((x^2) = \int_{-\infty}^{\infty} x^2 \frac{1}{\sqrt{\sigma}}e^{-\frac{x^2}{\sigma^2}} dx\)
Evaluating this integral gives us the value of \((x^2)\) for the ground state of the Harmonic Oscillator.
To evaluate \(\sigma_2\), we can simply take the square root of \((x^2)\) and subtract the expectation value of \(x\) squared, \((x)^2\).
(b) To evaluate \((p^2)\), we need to find the expectation value of \(p^2\) with respect to the wavefunction \(\psi_0(x)\). However, in this case, it is clear that the ground state of the Harmonic Oscillator is an eigenstate of the momentum operator, \(p\). Therefore, the expectation value of \(p^2\) for this state will simply be the eigenvalue corresponding to the momentum operator squared.
(c) The Heisenberg's uncertainty principle states that the product of the uncertainties in position and momentum (\(\Delta x\) and \(\Delta p\)) is bounded by a minimum value: \(\Delta x \cdot \Delta p \geq \frac{\hbar}{2}\).
To show that the uncertainty product satisfies the uncertainty principle, we need to calculate \(\Delta x\) and \(\Delta p\) for the ground state of the Harmonic Oscillator and verify that their product is greater than or equal to \(\frac{\hbar}{2}\).
If the ground state wavefunction \(\psi_0(x)\) is a Gaussian function, then the uncertainties \(\Delta x\) and \(\Delta p\) can be related to the standard deviation \(\sigma\) as follows:
\(\Delta x = \sigma\)
\(\Delta p = \frac{\hbar}{2\sigma}\)
By substituting these values into the uncertainty product inequality, we can verify that it satisfies the Heisenberg's uncertainty principle.
Regarding the statement \((x) = 0\) and \((p) = 0\) for this problem, it seems incorrect. The ground state of the Harmonic Oscillator does not have zero uncertainties in position or momentum. Both \(\Delta x\) and \(\Delta p\) will have non-zero values.
learn more about "wavefunction":- https://brainly.com/question/28447252
#SPJ11
yo please help me w dis asap!!!

Answers
Answer:
a = -4, b = 3, c = 6
Step-by-step explanation:
x² + 8x = 38
(x + 4)² - 16 = 38
(x + 4)² = 54
x + 4 = ± √54
x = -4 ± 3√6
If F(x)=-x+6 and g(x)=3x^2-x+3 find the value of (g•f)(8)
Answers
9514 1404 393
Answer:
-374
Step-by-step explanation:
f(8) = -8 +6 = -2
g(8) = (3x -1)x +3 = (3·8 -1)8 +3 = 23·8 +3 = 187
Then the product is ...
(g•f)(8) = g(8)•f(8) = 187·(-2)
(g•f)(8) = -374

What can be concluded about a pair of triangles with some congruent corresponding parts? Select all that apply.
The two triangles are sometimes congruent.
A conclusion cannot be made based on the given information.
The two triangles are always congruent.
The two triangles are never congruent.
Answers
Answer:
The two triangles are sometimes congruent.
Step-by-step explanation:
I did it and got it correct
The following assign labels for certain contents in the format of label : content. Input only the label associated with the correct content into each of the boxes:
i. Range (A)
ii. Null (A)
iii. Row (A)
iv. Null (A)
The equation Ax=b has a solution only when b is in____ it has a unique solution only when____ contains only the zero vector.
The equation ATy=d has a solution only when d is in___ it has a unique solution only when ____contains only the zero vector. Assume the size of A is m×n.
Assume the size of A is m x n then
when Ax=b has a unique solution, the space____ must be equal to Rn
Hint: any null vector of A must be orthogonal to the rows of A, and the null vector can only be a zero vector when the solution is unique
when ATy=d has a unique solution, the space___ must be equal to Rm Hint: any null vector of AT must be orthogonal to the rows of AT, and the null vector can only be a zero vector when the solution is unique.
Answers
i. Range (A): The space spanned by the columns of matrix A. It represents all possible linear combinations of the columns of A.
ii. Null (A): The set of all vectors x such that Ax = 0. It represents the solutions to the homogeneous equation Ax = 0.
iii. Row (A): The space spanned by the rows of matrix A. It represents all possible linear combinations of the rows of A.
iv. Null (A): The set of all vectors y such that ATy = 0. It represents the solutions to the homogeneous equation ATy = 0.
The equation Ax = b has a solution only when b is in the Range (A). It has a unique solution only when the Null (A) contains only the zero vector.
The equation ATy = d has a solution only when d is in the Row (A). It has a unique solution only when the Null (A) contains only the zero vector.
Assuming the size of A is m × n:
When Ax = b has a unique solution, the space Null (A) must be equal to Rn. This means there are no non-zero vectors that satisfy Ax = 0, ensuring a unique solution.
When ATy = d has a unique solution, the space Null (AT) must be equal to Rm. This means there are no non-zero vectors that satisfy ATy = 0, ensuring a unique solution.
Learn more about matrix from
https://brainly.com/question/27929071
#SPJ11
How should I explain how I got my answer?
Answers
Answer:
What is meant by "Explain your answer?"
On tests & problem sets students are often asked to explain the reasoning behind their answers. They are often frustrated and/or confused by “explain.” What & why are they supposed to explain? Here is one answer:
It isn't enough to get the right answer -- you have to be able to explain how you got it. To be sure you get enough practice at explaining yourself, it pays to discuss the questions with your fellow students and/or to write out explanations of your reasoning. You need to both
(1) Include the right facts, principles, etc., AND
(2) Explain the logic that you used to solve the problem. How did you get from the facts to the answer?
It is not sufficient to pile up unselected facts (even if they are correct), OR just to state the facts (even if they are the right ones), without explaining how they relate to the problem at hand, OR to just explain the logical train of thought (even if it is correct), without any specifics.
That's what you shouldn't do. What should you aim for??
Try to explain as if you were talking to a fellow student in the class who is generally intelligent, prepared, etc., but can't figure out this particular question. In other words, explain your reasoning step by step. Don't just repeat all the related facts in the book or notes--try to pick out the important, relevant points, put them in logical order, and explain (or diagram) how one leads to the next. (In other words, pretend you are writing a simple* answer key.)
*Note: The keys provided after each exam or problem set are usually quite complex and go beyond what we expect from an individual student. The posted keys tend to be so long and involved because they include not only correct answers (& explanations) but also explanations of common student misconceptions.
How to Get the Most out of Explaining
When you explain things to yourself, or to others, try not to use pronouns. Use nouns instead. This may sound silly, but it really helps you to be sure that you understand what you are saying. If you use pronouns or vague terms you can fool yourself into thinking you understand when you really don't. An example: Suppose you say "The gene is transcribed and it goes to the cytoplasm and is translated, which uses tRNA and mRNA." What do you mean by it and/or which? Is it the gene or the mRNA? Does which refer to translation or transcription? Sometimes you know, and you are just using shorthand. But sometimes you don't know, and you don't even realize it until you are forced to pick the right terms to replace "it" and "which." So try to be as specific as possible instead of as vague and as general as possible. Being specific has multiple advantages. It helps you to learn, it helps listeners understand what you are saying, and it helps graders on exams know that you really understand what you are talking about.
State if the three numbers can be the measures of the sides of a triangle,
6,8,9
No
Yes
Answers
help help help help help help help help help

Answers
Answer:
do math
Step-by-step explanation:
Find the common factor of all the terms of the polynomial 16x2 - 14x. O A. 2x² O B. 44² O c. 2x O D. 4x
Answers
Answer:
c. 2x.
Step-by-step explanation:
16x2 - 14x
Common factor of 16 and 14 = 2'
for x2 and x it is x,
Answer: 2x.
An antique vase was worth $185 when you inherited it from your grandma in
2007. In 2017, the vase is worth $325. Write and solve an equation to find how
much the vase should be worth in 2025
Answers
Answer:yes but that to is gonna get the same answer F(x) =1/2x+1/2
f-1(x) = [ ? ]x + [ ]
Step-by-step explanation:
Answer:
456,8
Step-by-step explanation:
325 / 185 / 10 * 8 * 325
Given m||n, find the value of x.
t
(7X+7)
(2x+2)
Answers
The value of x is 21.
From the attached diagram we can observe that the lines m and n are parallel to each other and these parallel lines are intersected by transversal t.
Let us assume that angle 'y' be a linear angle with (2x + 2)
(Both angles are below line n)
⇒ y + (2x + 2) = 180° .............(1)
So that, angles (7x + 7) and angle y are alternate exterior angles.
We know that alternate exterior angles are equal.
⇒ (7x + 7) = y
From equation (1),
(7x + 7) + (2x + 2) = 180°
9x + 9 = 180
9(x + 1) = 180
x + 1 = 20
x = 21
This is the required value.
Learn more about alternate exterior angles here:
https://brainly.com/question/2279752
#SPJ1
Find the complete question below.

Why does a plasmid that is going to be used in both yeast and bacteria need to have two different selection markers? Select ALL that apply. The same selection (e.g. presence of an antibiotic) may not work for both hosts. Having more genes makes the plasmid bigger and thus easier to work with and maintain. In cases where the same selection can be used in both hosts, two selection markers are still needed because bacteria and yeast recognize different promoters The codons used by bacteria correspond to different amino acids than they do in yeast.
Answers
A plasmid used in both yeast and bacteria requires two different selection markers because the same selection may not work for both hosts and bacteria and yeast recognize different promoters.
When using a plasmid in both yeast and bacteria, it is important to have two different selection markers for several reasons. First, the same selection, such as the presence of an antibiotic, may not be effective in both hosts. Different organisms have varying sensitivities to antibiotics, so a marker that works in bacteria may not work in yeast or vice versa. Therefore, two different selection markers are needed to ensure successful selection in both hosts.
Additionally, bacteria and yeast recognize different promoters, which are DNA sequences that control the initiation of gene expression. Promoters are specific to each organism and play a crucial role in regulating gene expression. By incorporating two different selection markers into the plasmid, each marker can be driven by a promoter recognized specifically by the corresponding host. This ensures that the selection marker is effectively expressed in the appropriate host organism, enabling accurate selection and maintenance of the plasmid.
In summary, using two different selection markers in a plasmid intended for both yeast and bacteria is necessary because the same selection may not be effective in both hosts, and different promoters are recognized by bacteria and yeast. This approach allows for successful selection and maintenance of the plasmid in both organisms.
To learn more about plasmid refer:
https://brainly.com/question/30313647
#SPJ11
Use the following statements to write a compound
statement for the disjunction -p or -q. Then find its truth
value.
p: There are 14 inches in 1 foot.
q: There are 3 feet in 1 yard.
Answers
The disjunction of -p or -q can be written as (-p) v (-q). So, we have to find the truth value of (-p) v (-q). So, the compound statement for the disjunction of -p or -q is (-p) v (-q), and its truth value is true.
using the following statements: p: There are 14 inches in 1 foot.
q: There are 3 feet in 1 yard.
Solution: We know that 1 foot = 12 inches, which means that there are 14 inches in 1 foot can be written as 14 < 12. But this statement is false because 14 is not less than 12. Therefore, the negation of this statement is true, which gives us (-p) as true.
Now, we know that 1 yard = 3 feet, which means that there are 3 feet in 1 yard can be written as 3 > 1. This statement is true because 3 is greater than 1. Therefore, the negation of this statement is false, which gives us (-q) as false.
Now, we can use the values of (-p) and (-q) to find the truth value of (-p) v (-q) using the disjunction rule. The truth value of (-p) v (-q) is true if either (-p) or (-q) is true or both (-p) and (-q) are true. Since (-p) is true and (-q) is false, the disjunction of (-p) v (-q) is true. Hence, the compound statement for the disjunction of -p or -q is (-p) v (-q), and its truth value is true.
For more questions on: compound statement
https://brainly.com/question/28794655
#SPJ8
Help please
Mathematics

Answers
Answer:
21.5sqft
Step-by-step explanation:
The area of the square is 10ft*10ft = 100sqft
The area of the circle is 5ft*5ft*pi = 25pi sqft
We're supposed to use 3.14 for pi, so the circle is around 25*3.14 sqft = 78.5sq ft
The area left over is 100sqft - 78.5sqft = 21.5sqft
Answer:
21.5 sq. feet
Step-by-step explanation:
Find area of squareFind area of circleSubtract area of circle from square to get area of remaining cloth
help me math home work part 3

Answers
Answer:9x^4
Step-by-step explanation:
6x^4*3x^3 can be simplified to 18x^7 by separating out cand combining like terms [6*3 = 18] and [x^4*x^3 = x^7]
This results in 18x^7 fr the top term
Do the same for the bottom term: 2x^2*x = 2x^3
We can now write: (18x^7)/(2x^3)
The reduces to 9x^4
The Hansons are having a well built in their backyard. On Monday, 175 feet of the well was dug, and another 165 feet was dug on Tuesday. How many feet below ground was the well dug, expressed as an integer The Answer would be 10.35
Answers
Answer:
340 feet
Step-by-step explanation:
To get the number of feet, we simply make an addition of the number of feet dug on both days
The total will be 175 feet + 165 feet = 340 feet
Bank ABC offers a 10 -year CD that pays a 5.0% interest compounded annually.
Bank XYZ also offers a 10 -year CD that pays 4.95% interest compounded daily.
How much would a $1,000 initial investment in each bank's CD be worth at maturity?
Bank ABC: ______
Bank XYZ: ______
(Enter answer in the form: $x,x×x.xx )
Answers
A $1,000 initial investment in Bank ABC's CD would be worth $1,628.89 at maturity. A $1,000 initial investment in Bank XYZ's CD would be worth $1,622.82 at maturity.
The formula to calculate the value of a CD after a specific duration at a specific interest rate compounded annually is given by:
A = P(1 + r/n)^(nt)
where P is the principal,
r is the annual interest rate,
n is the number of times compounded per year,
t is the number of years, and
A is the value of the CD at maturity.
Here, we need to calculate the value of a $1,000 initial investment in each bank's CD at maturity.
Let's calculate the value of a $1,000 investment in Bank ABC's CD.
P = $1,000
r = 5.0% compounded annually
t = 10 years
n = 1
We have all the values; let's put them in the formula and solve:
A = $1,000(1 + 0.05/1)^(1x10)A = $1,628.89
Therefore, a $1,000 initial investment in Bank ABC's CD would be worth $1,628.89 at maturity.
Let's calculate the value of a $1,000 investment in Bank XYZ's CD.
P = $1,000
r = 4.95% compounded daily
t = 10 years
n = 365
We have all the values; let's put them in the formula and solve:
A = $1,000(1 + 0.0495/365)^(365x10)A = $1,622.82
Therefore, a $1,000 initial investment in Bank XYZ's CD would be worth $1,622.82 at maturity.
To know more about investments, visit:
https://brainly.com/question/31411302
#SPJ11
Consider parallelogram ABCD. Which of the following transformations will change the perimeter of the parallelogram?
Answers
In geometry, transformation involves changing the position and/or size of a shape.
The transformation that will change the size of ABCD is dilation.
There are four transformations in geometry:
TranslationReflectionRotationDilationOf all types of transformation, dilation will change the size of the shape,
The new shape will either be enlarged or reduced
Either ways, the size of the shape will be altered.
When the size is altered, the perimeter will not remain the same.
Hence. dilation will change the perimeter of ABCD.
Read more about transformations at:
https://brainly.com/question/11709244
Which fraction is less?
5/12 or 6/10.
Answers
Answer:
\(\frac{5}{12}\)
Step-by-step explanation:
Make both fractions have a common denominator
\(\frac{5}{12}=\frac{50}{120}\)
\(\frac{6}{10}=\frac{72}{120}\)
Therefore, \(\frac{5}{12}<\frac{6}{10}\) since \(\frac{50}{120}<\frac{72}{120}\)
7/3 + x=3;x math I really need help
Answers
Given:
The equation is:
\(\dfrac{7}{3}+x=3\)
To find:
The value of x.
Solution:
We have,
\(\dfrac{7}{3}+x=3\)
Subtract both sides by \(\dfrac{7}{3}\).
\(\dfrac{7}{3}+x-\dfrac{7}{3}=3-\dfrac{7}{3}\)
\(x=\dfrac{9-7}{3}\)
\(x=\dfrac{2}{3}\)
Therefore, the value of x is \(\dfrac{2}{3}\) or it can be written as 0.667.
divided the fraations
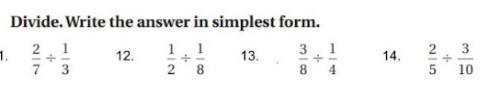
Answers
Answer:
please see detailed answers below
Step-by-step explanation:
to divide one fraction by another, just multiply the 2nd one upside down.
1) 2/7 ÷ 1/3 = 2/7 X 3/1 = 6/7
12) 1/2 ÷ 1/8 = 1/2 X 8/1 = 8/2 = 4
13) 3/8 ÷ 1/4 = 3/8 X 4/1 = 12/8 = 3/2
14) 2/5 ÷ 3/10 = 2/5 X 10/3 = 20/15 = 4/3
Nicole begins jogging for Mr. allergies class. on her first run, she runs one- half mile. she increases her work out by adding one-half mile a week to her run. she wrote the equation f(x) = 0.5 + 0.5x to model her progress. What does x represent?
A. Miles she runs.
B. Weeks she runs
C.miles she ran the first day
D. Calories she burns
Answers
What is the 50th term of the sequence that begins -6,0,6,12
a. 292
b. 288
c. 286
d. 290
Answers
Answer:
The 50th term of the sequence that begins with - 6 is 288.
Step-by-step explanation:
Definition of Arithmetic ProgressionAn arithmetic progression, also known as an arithmetic sequence, is a set of numbers in which the difference between successive terms remains constant. The sequence 5, 7, 9, 11, 13, 15,... is, for example, an arithmetic progression with a common difference of 2.
Formula -\($a_{n}=a_{1}+(n-1) d$\)
The given sequence is − 6, 0, 6, 12,It is in arithmetic progression as the common difference between all consecutive numbers is 6.
Let a1 be the first term and d be the common difference.
Therefore, a1 = - 6 and d = 6
For 50th term, a50 = a1 + (n - 1) d
= - 6 + (50 - 1) 6
= - 6 + 49 × 6
= - 6 + 294
= 288
Thus, the 50th term of the sequence is 288.
Learn more about arithmetic progression here-https://brainly.com/question/24462795
#SPJ2
An investment group compares returns on an account
against the function represented in the table, where x is the
time in years and f(x) is the total return on investment.
Which describes the function over the interval given in the
table?
х
a decreasing quadratic function
an increasing quadratic function
a decreasing exponential function
an increasing exponential function
0
5
f(x)
10,000
12,201.90
14,888.64
22,167.15
10
20
Answers
Answer:
d
Step-by-step explanation:
edge2020
Option D is correct. The exponential function is increasing when time goes and the total return on investment.
What is exponential function?An exponential function is of the form aˣ where 'a' is the base of the function and 'x' is the power of the function.
What is quadratic function?A quadratic function is" a polynomial function with one or more variables in which highest exponent of variable is 2".
According to the question,
Let 'x' is the time in years and f(x) is the total return on investment. The below table shows the function over the interval.
x f(x)
a decreasing quadratic function 10,000
an increasing quadratic function 12,201.90
a decreasing exponential function 14,888.64
an increasing exponential function 22,167.15
Quadratic function f(x) = ax² +b x +c a > 0
A decreasing quadratic function is the vertex of the parabola lies on the axis parabola. The graph of the function is increasing at one side of the axis and decreases at other side of the axis. Clearly it shows as time in years change does not give maximum total return on investment.An increasing quadratic function the vertex of the parabola lies on the axis parabola. The graph of the function is increasing at one side of the axis and decreases at other side of the axis. Clearly it shows change in time in years does not give maximum total return on investment.Exponential function f(x) = a. bˣ +q
The exponential function is decreasing when a < 0 and 0 ≤ b < 1. Then the function f(x) is decreasing exponential function. Clearly it shows time goes, total return on investment is not maximum. The exponential function is increasing when a > 0 and b > 1. Then the function f(x) is increasing exponential function. Clearly it shows time goes, total return on investment is maximum.Hence, the exponential function is increasing when time goes and the total return on investment.
Learn more about exponential function here
https://brainly.com/question/27307412
#SPJ2
Simplify the expression −|−5⋅(−7)|
Answers
Answer:
-35
Step-by-step explanation:
-|35|
-35
Answer:
-35
Step-by-step explanation:
−|−5⋅(−7)|
Multiply inside the absolute values
−|35|
Take the non negative value inside the absolute value
- 35
Fill out the Rate column in the table below.
a = b=
Answers
The rate column will be:
A= 30
B= 20
C= x miles
D= x miles
What is rate?It should be noted that rate simply means the measure, quantity, or frequency that one measure against another quantity or measure.
In this case, Jorden drives to the store at 30 miles per hour and on her way home she averages only 20 miles per hour.
Therefore, the rate column will be:
A= 30
B= 20
C= x miles
D= x miles
Learn more about rate on:
https://brainly.com/question/25537936
#SPJ1
Fill out the Rate column in the table below. Jorden drives to the store at 30 miles per hour. On her way home she averages only 20 miles per hour. If the total driving time takes half an hour, how far does she live from the store? Fill out the Rate column in the table below. a = b =
If the ratio 5:8 =× : 100 find the value of ×
Answers
Answer:
x = 62.5
Step-by-step explanation:
Express the ratios as equivalent fractions, that is
\(\frac{5}{8}\) = \(\frac{x}{100}\) ( cross- multiply )
8x = 500 ( divide both sides by 8 )
x = 62.5
Click on photo again (I’m so sorry but 20 point for it lol)
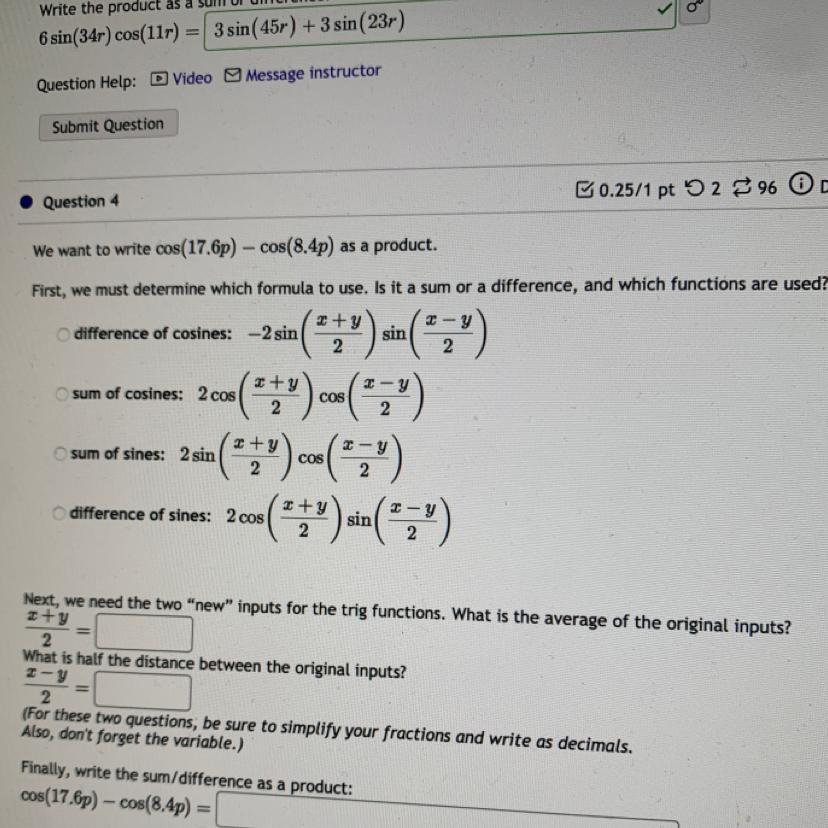
Answers
The formula to use to write cos(17.6p) + cos(8.4p) as a product is: B. sum of cosines: \(2cos(\frac{x\;+\;y}{2} )cos(\frac{x\;-\;y}{2} )\).
The average of the original inputs is \(\frac{x\;+\;y}{2} =13p\)
Half the distance between the original inputs is \(\frac{x\;-\;y}{2} =4.6p\)
The sum as a product is: cos(17.6p) + cos(8.4p) = 2cos(13p)cos(4.6p).
What is the Bhaskaracharya sum and difference formulas?In Mathematics and Geometry, the Bhaskaracharya sum and difference formulas that shows the relationship between sine and cosine values for trigonometric identities (two angles) can be modeled by the following mathematical equation;
cos(u + v) = cos(u)cos(v) - sin(u)sin(v)
cos(u - v) = cos(u)cos(v) + sin(u)sin(v)
cos(u + v) + cos(u - v) = 2cos(u)cos(v)
In this context, the formula to use in writing cos(17.6p) + cos(8.4p) as a product is given by:
sum of cosines: \(2cos(\frac{x\;+\;y}{2} )cos(\frac{x\;-\;y}{2} )\).
For the average of the original inputs, we have:
\(\frac{x\;+\;y}{2} =\frac{17.6\;+\;8.4}{2} \\\\\frac{x\;+\;y}{2} =13p\)
For half the distance between the original inputs, we have:
\(\frac{x\;-\;y}{2} =\frac{17.6\;-\;8.4}{2} \\\\\frac{x\;-\;y}{2} =4.6p\)
Therefore, the sum as a product can be written as follows:
cos(17.6p) + cos(8.4p) = 2cos(13p)cos(4.6p).
Read more on sum of cosines here: https://brainly.com/question/25312045
#SPJ1
Find the 4th term in the sequence with the following definition help meeeeeeeeee

Answers
Answer:
-37.
Step-by-step explanation:
a2 = 2 a2-1 - 3
= 2 a1 - 3
= 2*-2 -3
= -7
a3 = 2 a3 - 3
= 2*-7 - 3
= -17
4th term a4
= 2*-17 - 3
= -37.