Answers
Related Questions
A gas station is supplied with gasoline once a week and the weekly volume of sales in thousands of gallons is a random variable with probability density function (pdf) fx(x) A (1x)*, lo, 0 x 1 otherwise (a) What is the constant A? (b) What is the expected capacity of the storage tank? (c) What must the capacity of the tank be so that the probability of the supply being exhausted in a given week is 0.01?
Answers
(a) To find the
constant
A, we need to integrate the given pdf from 0 to 1 and set it equal to 1, since the total
probability
of all possible outcomes must be 1:
∫[0,1] A(1/x) dx = 1
Using the fact that ln(1/x) is the antiderivative of 1/x, we get:
A[ln(x)]|[0,1] = 1
A[ln(1) - ln(0)] = 1
A(0 - (-∞)) = 1
A = 1
Therefore, the constant A is 1.
(b) The expected capacity of the storage tank is the expected value of the random variable, which is given by:
E(X) = ∫[0,1] x f(x) dx
Using the given pdf, we get:
E(X) = ∫[0,1] x (1/x) dx = ∫[0,1] dx = 1
Therefore, the expected capacity of the storage tank is 1 thousand gallons.
(c) Let C be the capacity of the tank in thousands of gallons. Then, the probability that the supply is exhausted in a given week is the probability that the weekly sales exceed C, which is given by:
P(X > C) = ∫[C,1] f(x) dx
Using the given pdf, we get:
P(X > C) = ∫[C,1] (1/x) dx = ln(1/C)
We want P(X > C) = 0.01, so we solve the equation ln(1/C) = 0.01 for C:
ln(1/C) = 0.01
1/C = e^0.01
C = 1/e^0.01
Rounding this to 3 decimal places, we get:
C ≈ 0.990
Therefore, the capacity of the tank must be at least 0.990 thousand gallons to ensure that the probability of the supply being exhausted in a given week is no more than
0.01
.
Learn more about
Volume
here:- brainly.com/question/1825045
#SPJ11
HURRY !! A female blue jay is generating an egg cell for reproduction. Through which process does the egg cell form?
meiosis
prophase
fertilization
mitosis
Answers
Answer: Meiosis
Step-by-step explanation: Meiosis is the type of cell division that creates egg and sperm cells.
Answer: meiosis
Step-by-step explanation:
Si 10 barras de chocolate cuestan 3 pesos, ¿cuánto cuesta 1?
Answers
To know how much each chocolate bar costs, knowing that ten chocolate bars cost 3 pesos, we only have to divide the total cost of the 10 chocolate bars by the total number of chocolate bars.
So that:
3 pesos ➗ 10 bars = 0.3 pesos/bar.Tenth that; the cost of each bar is 0.3 pesos.
suppose that a recent article stated that the mean time spent in jail by a first-time convicted burglar is 2.5 years. a study was then done to see if the mean time has increased in the new century. a random sample of 27 first-time convicted burglars in a recent year was picked
Answers
We can reject the null hypothesis at the 0.05 level and accept the alternative hypothesis.
A one-sided test will test using the full alpha to test whether the result is far enough in one direction. A two-sided test will split the alpha in half to test whether the result is too big or too small.
The null hypothesis is:
\(\mathit{H}_{0}: \mu= 2.5\)
The alternative hypothesis is:
\(\mathit{H}_{1}: \mu > 2.5\)
The z-score for a mean of 3 is:
\(z = (x- \mu)/ (\sigma/ \sqrt{n})) \\ = (3-2.5)/(1.8/\sqrt{n})) \\ = (.5)/(1.8/6)) \\ = (.5)/(.3)) \\ = 1.666666667\)
The z-score for the 0.05 significance level is 1.645, which is less than the mean of 3 z score of 1.67.
Hence, we can go ahead and reject the null hypothesis
Learn more about hypothesis:
https://brainly.com/question/29519577
#SPJ4
The weight of chocolate bars from a particular chocolate factory has a mean of 8 ounces with a standard deviation of 0. 1 ounces. What is the z-score corresponding to a weight of 8. 17 ounces? What percent of chocolate bars weigh less than 8. 17 ounces. Show and explain your work
Answers
95.54% of the chocolate bars at the factory weigh less than 8. 17 ounces
What is an equation?An equation is an expression showing the relationship between two or more numbers and variables. An equation can either be linear, quadratic, cubic and so on depending on the degree.
z score shows by how many standard deviations the raw score is above or below the mean. It is given by:
z = (raw score - mean)/standard deviation
Given that mean = 8, standard deviation = 0.1
For x < 8.17 ounces:
z = (8.17 - 8) / 0.1 = 1.7
From the normal distribution table:
P(z < 1.7) = 0.9554 = 95.54%
The probability that the chocolate bars weigh less than 8. 17 ounces is 95.54%
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
PLEASE HELP
What is the approximate volume of the cone
Use 3.14 for TT.
57 cm3
339 cm3
509 cm3
1526 cm3
Answers
The volume of the Illustrated cone used as an example is 51.3cm³.
How to calculate the volume?Volume is a measurement of three-dimensional space that is occupied. It is frequently expressed numerically using SI-derived units, as well as different imperial or US-standard units. Volume and the definition of length are related.
A cone is a recognizable three-dimensional geometric shape with a flat and curved surface that is pointed upward. The formula for the volume of a cone is V=1/3hπr²
Let's say the radius is 7cm. The volume will be:
= 1/3 × 3.14 × 7²
= 51.3cm³
Learn more about volume on:
https://brainly.com/question/28790396
#SPJ1
Complete as a indirect proof
1. S ⊃ D (TV ~U) 2. U ⊃ D ( ~T V R) 3. (S & U) ⊃ ~R /~S V~U
Answers
To complete the indirect proof, also known as proof by contradiction, we assume the opposite of the desired conclusion and derive a contradiction from it. In this case, we assume ~(~S V ~U) and aim to derive a contradiction.
Assume ~(~S V ~U). Using De Morgan's law, we can rewrite this as (S & U). From the premises, we have:
1. S ⊃ D (TV ~U)
2. U ⊃ D (~T V R)
3. (S & U) ⊃ ~R (given, not ~R)
We will now derive a contradiction:
4. ~R (modus ponens: 3, S & U)
5. ~T V R (modus ponens: 2, U)
6. ~T (disjunctive syllogism: 4, 5)
7. TV ~U (modus ponens: 1, S)
8. U (simplification: S & U)
9. ~U (disjunctive syllogism: 4, 8)
From step 8 and step 9, we have both U and ~U, which is a contradiction.
Since we derived a contradiction from the assumption ~(~S V ~U), our initial assumption must be false. Therefore, the conclusion ~S V ~U must be true.
Hence, the indirect proof demonstrates that ~S V ~U is true.
To know more about De Morgan's law:
https://brainly.com/question/29073742
#SPJ11
PLS HELP MEEE I NEED THE ANSWERS RN

Answers
Answers:
x= -10 and y= 16
3y = -6x - 12
3y = -6(-2y+22) -12
3y = 12y - 144
3y + -12y = 12y -144 + -12y
-9y = -144
divide -9 on both sides
y= 16
x= -2y+22
x= -2y+22
x= (-2)(16)+22
x= -10
PLEASE HELP!!
The diagram shows the cross-section ABCD of a sculpture in the shape of
a prism
with perpendicular height 9 cm.
AB = 14 cm, CD = 8cm, AD = 12cm and BC = 10cm
The height of the prism is also 9 cm.
What is the total surface area of the sculpture in cm2?
Type each step of your working on a separate line.

Answers
Answer:
99 (cm^2)
Step-by-step explanation:
Perpendicular to the AB segment at points D and C, the graph is divided into two triangles and a rectangle.
The area of the middle rectangle is equal to 8*9=72. The hypotenuse of the right triangle is 10cm, and one of the right sides is 9cm, so the other side is SQRT (10^2-9^2) = SQRT (19).
One side of the left triangle is 9cm long and the other side is 14-8-sqRT (19) = 6-sqRT (19) cm.
Then, add the area of the three parts.
72+9*sqrt(19)/2+9*(6-sqrt(19))/2=99 (cm^2)
Latex: \triangle ABC
△
A
B
C
was transformed using two rigid transformations.
a. Compare all of the corresponding parts (angles and sides) of the image and preimage. Describe the results.
b. Explain why the results are true.
When two triangles are congruent to each other, each triangle has six parts (three angles and three sides) that are congruent to those six parts of the other triangle. This can be proven using rigid transformations. But suppose you don't know the rigid transformations that map one triangle to another.
a. How can you prove the two triangles are congruent without using rigid transformations?
b. Will you need to show that all of the parts of one triangle are congruent to all of the parts of the other triangle to prove they are congruent? Explain.
Answers
a. The corresponding parts (angles and sides) of the image and preimage of triangle ABC are congruent after two rigid transformations. b. The congruence of the corresponding parts is true because rigid transformations preserve the shape and size of geometric figures.
a. When comparing all corresponding parts (angles and sides) of the image and preimage of triangle ABC after two rigid transformations, we observe that they are congruent. This means that the corresponding angles and sides of the transformed triangle match exactly with the corresponding angles and sides of the original triangle.
b. The results are true because rigid transformations (such as translations, rotations, and reflections) preserve the shape and size of geometric figures. In other words, these transformations do not alter the angles and lengths of the original triangle. As a result, the transformed triangle remains congruent to the original triangle.
To prove that two triangles are congruent without using rigid transformations:
a. You can use other methods of congruence, such as side-angle-side (SAS), angle-side-angle (ASA), or side-side-side (SSS) congruence. These methods involve comparing specific combinations of angles and sides between the triangles.
b. No, it is not necessary to show that all parts of one triangle are congruent to all parts of the other triangle to prove their congruence. Depending on the given information, you can use the appropriate congruence criteria (such as SAS, ASA, or SSS) to establish the congruence of the triangles based on the specific combinations of angles and sides that are known or given.
To know more about rigid transformations,
https://brainly.com/question/30063622
#SPJ11
The weights of certain candles are normally distributed with a mean of 720mg and a standard deviation of 20mg. What proportion of candles weigh between 695mg and 734mg?
Answers
Answer:
ufoufoydiyd8yf86fiyxitdkydyofiyd8yfoyfoycoycoycoycoyfiyfiyfyocyiciycigxitc8txitditxt8xtix8tx8td8yd8yc8yyc8yf58d8txt7x85d85duts7td8txits
Step-by-step explanation:
yfid8yydyofoyf0
Find the perimeter. Explain what you added together to get your answer. You can get partial credit for explaining steps, even if your final answer is incorrect.

Answers
Answer:
the area of the shape is 7.14
Step-by-step explanation:
First, find the area of the square:
2 in x 2 in = 4 in
then to find the area of the semi- circles add them together to make a circle
To find the area of the circle, use:
pi x radius^2
Since the diameter is 2 divide the diameter by 2 to get radius
3.14 x 1^2 = 3.14
The circle is 3.14 plus 4 ( the square ) = 7.14
How are the roots of the equation x^2-2x-15=0 related to the function y=x^2-2x-15
Answers
Answer:
They are zeroes when y=0
Step-by-step explanation:
For a function \(f(x)\), if \(f(x)=0\), the values of x that make the function true are known as roots, or x-intercepts, or zeroes.
What are the 3 ways in math?
Answers
Step-by-step explanation:
Today, we are going to be talking about the three-way principle of mathematics. Basically, there are three ways to solve a problem in math: verbally, graphically, or by example. In this lesson, we will discuss each of these principles by solving sample problems using each type.
Two equations are shown: I will give 40 pts if someone answers
Equation 1: (x – 12) = 12
Solve each equation.
Answers
Answer:
x and y both equal 24
The table below represents a quadratic function. Use the data in the table to
determine the domain and range of the function.
x
-1
0
1
4
y
5
3
5
35

Answers
The domain is all real numbers and the Range is y ≥ 3.The correct answer is option A.
To determine the domain and range of the quadratic function based on the given table, let's analyze the values.
Domain represents the set of possible input values (x-values) for the function.
Range represents the set of possible output values (y-values) for the function.
From the given data:
x = -1, 0, 1, 4
y = 5, 3, 3, 5, 35
Looking at the x-values, we can see that the function has values for all real numbers. Therefore, the domain of the function is "all real numbers."
Now, let's consider the y-values. The minimum value of y is 3, and there are no y-values less than 3.
Additionally, the maximum value of y is 35. Based on this information, we can conclude that the range of the function is "y ≥ 3" since all y-values are greater than or equal to 3.
Therefore, the correct answer is:A. Domain: all real numbers
Range: y ≥ 3
For more such questions on Range,click on
https://brainly.com/question/30389189
#SPJ8
The probable question may be:
The table below represents a quadratic function. Use the data in the table to determine the domain and range of the function.
x= -1,0,1,4
y= 5,3,3,5,35
A. Domain: all real numbers Range: y ≥3
B. Domain: all real numbers
Range: x≥0
c. Domain: all real numbers
Range: y ≥0
D. Domain: all real numbers
Range: y ≤3
What are the values of x and y?
A.
x equals 136 over 15 and y equals 17 over 15
B.
x equals 64 over 15 and y equals 17 over 15
C.
x equals 8 over 15 and y equals 136 over 15
D.
x equals 64 over 15 and y equals 136 over 15

Answers
Answer:
d. 8 over 15 = 136 over 15 this is the right answer okay
PLEASE HELP ITS URGENT!
Considering line BD as a side of ABD, express its length in terms of variables representing side lengths and angle measures in ABD. Show your work.

Answers
Answer:
Thats the answer from american school
Step-by-step explanation:

The value of the common length BD would be 8 units aprroximately.
What are trigonometric identities?Trigonometric identities are the functions that include trigonometric functions such as sine, cosine, tangents, secant, and, cot.
Given information;
1. Considering line BD as a side of ABD, express its length in terms of variables representing side lengths and angle measures in ABD.
So, We know that
Sin A = BD / AB
Sin A = BD / c
c Sin A = BD
Substitute;
(10) Sin (53.13) = BD
BD = 10 ( 0.79)
BD = 7.99
Therefore, the value of the common length BD would be 8 units aprroximately.
Learn more about trigonometric;
https://brainly.com/question/21286835
#SPJ2
A person on the 25th floor of a building releases a quarter out of their window. The height of the quarter(in feet) is represented with the polynomial shown below, where t is the number of seconds after the quarter is released. At the same time, a person on the 20th floor throws a dime out of their window. The height of the dime( in feet) is represented by the polynomial shown in the photo attached.

Answers
The height of the quarter is given by the polynomial -16t^2 + 250 feet and the height of the dime is given by the polynomial -16t^2 - 10t + 100 feet.
To compare the height of the quarter and dime at any time t, we need to find the difference between their heights.
Let's first find the height of the dime when the quarter is released, which is at t=0:
Height of the quarter at t=0: 16(0)^2 + 250 = 250 feet
Height of the dime at t=0: -16(0)^2 - 10(0) + 100 = 100 feet
So, the initial height difference between the quarter and dime is 250 - 100 = 150 feet.
Now, let's find the height difference between the quarter and dime at any time t:
Height of the quarter at time t: 16t^2 + 250
Height of the dime at time t: -16t^2 - 10t + 100
So, the height difference at time t is:
(16t^2 + 250) - (-16t^2 - 10t + 100) = 32t^2 + 10t + 150
Therefore, the height difference between the quarter and dime at any time t is given by the polynomial 32t^2 + 10t + 150.
Leaen more about polynomial here:
https://brainly.com/question/11536910
#SPJ1
What is 0.025m in centimeters?
Answers
Answer:2.5cm
Step-by-step explanation:1cm =0.01 m
Estimate $10.01 + $7.07 using front-end estimation.
Answers
Answer:
17
Step-by-step explanation:
You would make the 10.01 a 10 and the 7.07 a 7.
What is the slope of the line?
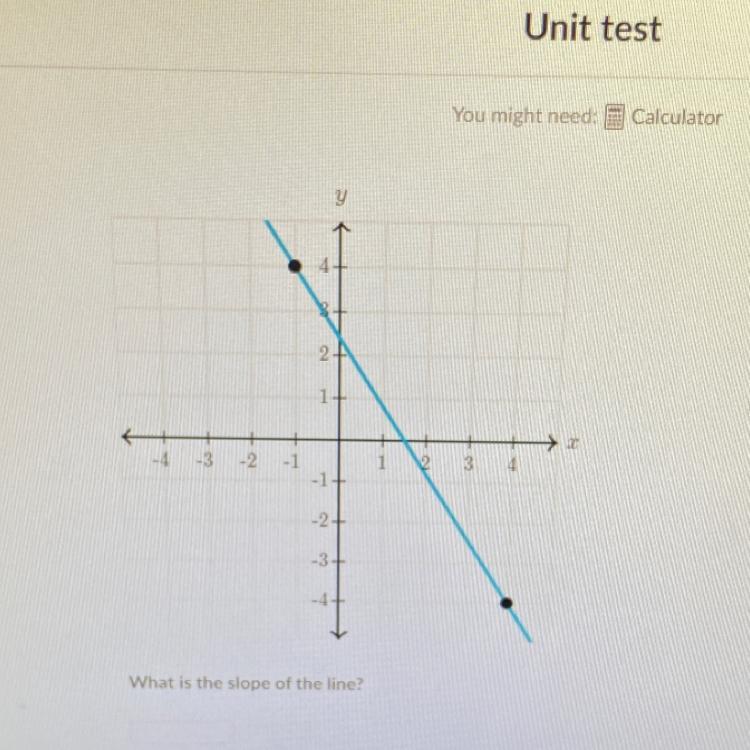
Answers
Answer:-8\5
Step-by-step explanation down 8 to the left 5
Whenever the probability is proportional to the length of the interval in which the random variable can assume a value, the random variable is
a. uniformly distributed
b. normally distributed
c. exponentially distributed
d. Poisson distributed
Answers
a. uniformly distributed. When the probability is proportional to the length of the interval in which the random variable can assume a value, the random variable is said to be uniformly distributed.
In a uniform distribution, the probability density function is constant within the interval, meaning that all values within the interval have an equal chance of occurring.
The uniform distribution is characterized by a rectangular-shaped probability density function, where the height of the rectangle represents the probability and the width of the rectangle represents the interval. This distribution is often used when there is no specific bias or preference for any particular value within the interval.
On the other hand, the normal distribution (b) follows a bell-shaped curve, the exponential distribution (c) describes the time between events in a Poisson process, and the Poisson distribution (d) is used to model the number of rare events occurring in a fixed interval of time or space.
Therefore, the random variable is uniformly distributed (a) when the probability is proportional to the length of the interval.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
Assuming that all years have 365 days and all birthdays occur with equal probability, how large must n be so that in any randomly chosen group of n people, the probability that two or more have the same birthday is at least 1/2?
Answers
it is seen that if the number of people in the group is n = 23, the probability that at least two people will have the same birthday is at least 1/2.
Let P(A) be the probability that in a randomly selected group of n people, at least two people have the same birthday.
If we assume that the year has 365 days, then the number of ways to select n people with different birthdays is n x (n-1) x (n-2) x ... x (n-364).
the probability of selecting n people with different birthdays is P(A') = n(n - 1)(n - 2)...(n - 364)/365nThen, the probability that at least two people in a group of n have the same birthday is given by P(A) = 1 - P(A').
We need to find the smallest value of n such that P(A) ≥ 1/2.Let's solve for this.Let us find n such that P(A) ≥ 1/2.
By using the complement rule, 1-P(A') = P(A).Then:1 - n(n - 1)(n - 2)...(n - 364)/365n ≥ 1/2n(n - 1)(n - 2)...(n - 364)/365n ≤ 1/2(2)n(n - 1)(n - 2)...(n - 364) ≤ 365n/2Now, take the natural logarithm of both sides and simplify as follows:ln[n(n - 1)(n - 2)...(n - 364)] ≤ ln[365n/2]nln(n) - ln[(n - 1)!] - ln[(n - 2)!] - ... - ln[2!] - ln[1!] ≤ ln[365n/2]
Therefore, we need at least 23 people in the group for the probability of two or more people having the same birthday to be at least 1/2.
This is because n = 23 is the smallest number for which the inequality holds, and therefore, it is the smallest number of people required to ensure that the probability of two or more people having the same birthday is at least 1/2.
To know more about number visit:
brainly.com/question/3589540
#SPJ11
a fair die is rolled five times. what is the probability that 6 lands face up at least once in the five rolls?
Answers
The probability that 6 lands face up at least once in the five rolls of a fair die is 0.4643 or 46.43%.
First of all, let's find out the total number of outcomes possible when a fair die is rolled 5 times.
The number of possible outcomes for a single roll of a die is 6.
Thus, the total number of outcomes possible for 5 rolls of a die will be \(6^5 = 7776.\)
Next, let's find out the number of outcomes in which no 6 lands face up.
The probability of not getting a 6 in a single roll is 5/6 (since there are 5 faces other than 6 on the die).
Thus, the probability of not getting a 6 in any of the 5 rolls is\((5/6)^5\).
So, the number of outcomes in which no 6 lands face up will be: \(7776 x (5/6)^5 = 4165.08\)
Now, let's find out the number of outcomes in which at least one 6 lands face up.
This will be the total number of outcomes minus the number of outcomes in which no 6 lands face up.
So, the number of outcomes in which at least one 6 lands face up will be:
7776 - 4165.08 = 3610.92.
Thus, the probability of getting at least one 6 in 5 rolls of a die will be:
3610.92/7776 = 0.4643 (rounded to 4 decimal places).
For similar question on probability.
https://brainly.com/question/12283505
#SPJ11
4 x 6 - 8 / 4 = help me out
Answers
Answer:
22
Step-by-step explanation:
You use the order of operations: PEMDAS.
Sooo...
4*6-8/4=
24-8/4=
24-2=
22
The following equation describes the motion of a certain mass connected to a spring, with viscous friction on the surface 3ÿ + 18y + 102y = f(t) where f(t) is an applied force. Suppose that f(t) = 0 for t <0 and f(t) = 10 for t≥ 0. a. Plot y(t) for y(0) = y(0) = 0. b. Plot y(t) for y(0) = 0 and y(0) =
Answers
The plot of y(t) will show how the mass oscillates with time, starting from the equilibrium position and gradually coming to rest due to the damping effect of the friction.
The given equation represents the motion of a mass connected to a spring with viscous friction. To plot the displacement, y(t), we need to solve the differential equation. With initial conditions y(0) = 0, we can find the solution using the Laplace transform. After solving the equation, we can plot y(t) for t < 0 and t ≥ 0 separately. For t < 0, the applied force, f(t), is zero, so the mass will not experience any external force and will remain at rest. For t ≥ 0, the applied force is 10, and the mass will respond to this force and undergo oscillatory motion around the equilibrium position.
To solve the given differential equation, we can start by finding the characteristic equation by setting the coefficients of y, its derivative, and its second derivative to zero:
s^2 + 18s + 102 = 0.
Solving this quadratic equation gives us the roots s1 = -3 + 3i and s2 = -3 - 3i. These complex roots indicate that the mass will undergo damped oscillations.
Using the Laplace transform, we can solve the differential equation and obtain the expression for Y(s), the Laplace transform of y(t):
(s^2 + 18s + 102)Y(s) = F(s),
where F(s) is the Laplace transform of f(t). Since f(t) = 10 for t ≥ 0, its Laplace transform is F(s) = 10/s.
Solving for Y(s) gives us:
Y(s) = 10 / [(s^2 + 18s + 102)].
To find y(t), we need to inverse Laplace transform Y(s). Using partial fraction decomposition, we can express Y(s) as:
Y(s) = A / (s - s1) + B / (s - s2),
where A and B are constants to be determined. After finding A and B, we can inverse Laplace transform Y(s) to obtain y(t).
With the given initial condition y(0) = 0, we can solve for A and B by setting up equations using the initial value theorem:
A / (s1 - s1) + B / (s1 - s2) = 0,
A / (s2 - s1) + B / (s2 - s2) = 0.
Solving these equations will give us the values of A and B. Finally, we can substitute these values back into the inverse Laplace transform of Y(s) to obtain y(t).
For t < 0, since the applied force f(t) is zero, the mass will not experience any external force. Therefore, y(t) will remain at its initial position, y(0) = 0.
For t ≥ 0, the applied force f(t) is 10, and the mass will respond to this force and undergo oscillatory motion around the equilibrium position. The displacement, y(t), will depend on the properties of the mass, the spring, and the viscous friction. The plot of y(t) will show how the mass oscillates with time, starting from the equilibrium position and gradually coming to rest due to the damping effect of the friction.
Learn more about equation here: brainly.com/question/29657983
#SPJ11
There are 8 cupcakes on a plate. Five children will share them equally. How many cupcakes will each child receive? Represent the scenario three ways:
With math vocabulary, as an expression, and as a fraction.
Answers
Answer:
Each child will receive eight fifths of the cupcakes.
5x=8 ; x represents how many cupcakes each child receives.
\(\frac{8}{5}\)
Step-by-step explanation:
There are 8 cupcakes in total.
5 children.
Divide 8 by 5. \(\frac{8}{5}\)
I hope this helps!
pls ❤ and mark brainliest pls!
please please help me it's for my homework

Answers
Answer:
6/25
Step-by-step explanation:
.24 = 24/100 = 6/25
Answer:
6/25
Step-by-step explanation:
step 1 The decimal number = 0.24
step 2 Write it as a fraction
0.24/1
step 3 Multiply 100 to both numerator & denominator
(0.24 x 100)/(1 x 100) = 24/100
It can be written as 24% = 24/100 or 24/100
step 4 To simplify 24/100 to its lowest terms, find LCM (Least Common Multiple) for 24 & 100.
4 is the LCM for 24 & 100
step 5 divide numerator & denominator by 4
24/100 = (24 / 4) / (100 / 4)
= 6/25
6/25 is a simplest fraction for the decimal point number 0.24
12 flowers are planted in a squared garden.How many garden are needed for this purpose?
Answers
answer:
tell us why the other gardens are needed
