Hover-high helicopters manufactures radio-controlled toy helicopters. they have their quality control down to a point where only 1 in 100 built could be defective and returned for repair at a cost to the company of $50. at a profit margin of $10 per unit, what would their profit be per unit after selling 200 copters?
a. -$9.40 per unit
b. $0.60 per unit
c. -$0.60 per unit
d. $9.40 per unit
e. $10.00 per unit
Answers
After selling 200 copters, Hover-high Helicopters would have a profit of $9.40 per unit. Therefore, the correct answer is d) $9.40 per unit.
To calculate the profit per unit, we need to consider the profit from each unit sold and subtract the cost of any defective units returned for repair.
Hover-high Helicopters has a defect rate of 1 in 100, which means that 1% of the units built are expected to be defective. With 200 copters sold, we can expect 2 units to be returned for repair (200 * 1% = 2).
For each unit sold, Hover-high Helicopters earns a profit margin of $10. However, they incur a cost of $50 for each defective unit returned for repair.
Profit per unit = Profit margin - Cost of defective units
= $10 - ($50 * Number of defective units)
Since 2 units are expected to be defective, the cost of defective units is $50 * 2 = $100.
Profit per unit = $10 - $100 = -$90.
However, the question asks for the profit per unit, so we need to consider the overall profit after selling 200 copters.
Profit per unit after selling 200 copters = Overall profit / Number of units sold
= (-$90 * 2 + $10 * 200) / 200
= ($-180 + $200) / 200
= $20 / 200
= $0.10
Therefore, the profit per unit after selling 200 copters is $0.10, which is equivalent to $9.40 per unit. The correct answer is d) $9.40 per unit.
Learn more about cost here:
https://brainly.com/question/19261126
#SPJ11
Related Questions
3x5+9^2/(27x1 third)-negative 10
Answers
The solution to the algebraic expression 3 × 5 + (9²/(27 × ¹/₃)) - (-10) using order of operations is; 34
How to carry out order of operations?The order of operations is mathematical operations is as follows: PEMDAS which denotes parentheses, exponents, multiplication, division, addition, then subtraction.
We want to solve the algebraic expression;
3 × 5 + (9²/(27 × ¹/₃)) - (-10)
Let us first solve the numerator to get;
15 + (81/(27 × ¹/₃)) - (-10)
Let us now solve the denominator to get;
15 + (81/9) + 10
= 15 + 9 + 10
= 34
Read more about order of operations at; https://brainly.com/question/17297306
#SPJ1
what is th answer to this question

Answers
The total surface area of the trapezoidal prism is S = 3,296 inches²
Given data ,
Let the total surface area of the trapezoidal prism is S
Now , the measures of the sides of the prism are
Side a = 10 inches
Side b = 32 inches
Side c = 10 inches
Side d = 20 inches
Length l = 40 inches
Height h = 8 inches
Lateral area of prism L = l ( a + b + c + d )
L = 40 ( 10 + 32 + 10 + 20 )
L = 2,880 inches²
Surface area S = h ( b + d ) + L
On simplifying the equation , we get
S = 2,880 inches² + 8 ( 52 )
S = 3,296 inches²
Hence , the surface area of prism is S = 3,296 inches²
To learn more about surface area of prism click :
https://brainly.com/question/9183590
#SPJ1
Hazel is trying to solve this inequality. After she solves it, she shows it to you, and she asks you if she did it correctly. This is the work she completed:
3(t+1)−4t≥−5
3(t+1)−4t≥−5
Step 1: 3t +3−4t≥−5
Step 2: −t+3≥−5
Step 3: −t≥−8
Step 4: t≥8
Part A: In which step did Hazel make a mistake?
Part B: How would you explain to Hazel what her mistake was, so she won't make the mistake again on a future test?
Answers
We need to see Hazel's work for simplifying an inequality and see if she had a mistake or not.
The answers are:
a) Step 4.
B) She did not change the direction of the inequality symbol.
a) Let's analyze each step:
She starts with:
3*(t + 1) - 4*t ≥ −5
Step 1:
3t +3−4t ≥ −5
Here what she does is distributing the first product, she goes from:
3*(t + 1) to 3*t + 3
Step 2:
−t+3≥−5
Here what she did is adding "3*t - 4*t = (3 - 4)*t = -t"
Step 3:
−t ≥ −8
Here she subtracts 3 in both sides.
Step 4:
t ≥ 8
Here is the mistake.
B)
Here what she does is multiplying by -1 in both sides, her mistake is that we multiply both sides by a negative number in an inequality, the direction of the inequality must change, so here is her error.
So what she actually should had is:
-t ≥ -8
(-1)*(-t) ≤ (-1)*(-8)
t ≤ 8
If you want to learn more, you can read:
https://brainly.com/question/20271304
5) The floor of a room is in the shape of
a rectangle. The room is c meters long
and the width of the room is 2cm less
than its length.
a) write in terms of c;
i) the width of the floor
ii) the area of the floor
b) If the area of the room is 15cm²,
write down an equation in c to show
this information.
c) Use the equation to find the length
and width of the room.
Answers
Answer: a) i) The width of the floor can be expressed in terms of c as: w = c - 2 cm.
ii) The area of the floor can be expressed in terms of c as: A = c * (c - 2) cm^2.
b) If the area of the room is 15 cm^2, then we can write the equation as:
c * (c - 2) = 15.
c) Solving for c, we get:
c^2 - 2c - 15 = 0.
Using the quadratic formula, we find that:
c = 5 or c = -3.
Since the length of the room cannot be negative, we choose c = 5.
Therefore, the length of the room is 5 cm and the width of the room is 3 cm.
Step-by-step explanation:
Given ABCD, solve for x.
B
16. 2x
с
12
12
A
10 + 8x
D
O A. 1
O B. 3
C. 2
O D. 4
Answers
Answer: A
Step-by-step explanation:
X=1
Bill and Tom together have 112 baseball cards. Bill has 28 more than tom. How many does each boy have?
Define a variable, write an equation, and solve the problem
(Unit: Solving Equations: Variables on Both Sides)
Answers
Answer:
Let Cards with Tom be x
Therefore ,
Cards with Bill=x+28
No. of cards in total=112
x+x+28=112
2x=84
x=42.
Therefore,
Cards with Tom=42
Cards with Tom=42Cards with Bill=70
8. The graph below represents the path of a golf ball.
The Path of a Golf Ball
Part A: The above graph is (circle one) linear/nonlinear.
Part B: Is the above graph a function? Explain.
Part C: What is the y-intercept and what does the y-intercept
representa
Part D: What is the solution to this graph and what does it represent in this
situation?

Answers
Answer:
Part A: Non linear
Part B: Yes
Part C: The y-intercept is (0, 0), represent the starting height level of the golf ball
Part C: The solution are the points (0, 0) and (100, 0) which are the points at which the golf ball touches the ground
Step-by-step explanation:
Part A: The shape of the path of the increase in the height of the the golf ball as it moves in increasing horizontal distance from the starting point is hat of a parabola
Part B: The graph is a function because each value of the independent variable, distance (ft.) maps to exactly one value of the dependent variable, elevation (ft.)
Part C: The y-intercept represents the starting or initial value of the function, where x = 0. It represents the height from which the golf ball motion path starts
Part D: The solution represents the values of the x-intercept at which the elevation is the y = 0.
Every math class is made up of 18 twelve graders and 4 eleventh graders. The twelve grades averaged a 83, on the midterm exam, and the eleventh graders averaged a 79 on the midterm exam. What was the average grade on the midterm exam for the entire class? Round to the nearest whole number.
Answers
The average midterm exam grade for the entire class is 82.
What is average?The middle value in a set of numbers is the average, which is calculated by dividing the total of all the values by the number of values.
Here given that,
Math class contains 18 twelve graders.
Also contains 4 eleventh graders
Total number of students = 18 + 4 = 22
Total marks of students in the twelve grade = 18 x 83 = 1494
Total marks of students in the eleventh grade = 4 x 79 = 316
Total marks = 1494 + 316 = 1810
Therefore to find the average grade of midterm exam is :
1810 / 22 = 82.2
Therefore the average grade on the midterm exam for the entire class is 82.
To learn more about average refer to :
https://brainly.com/question/29220030
#SPJ1
Divide £144 in the ratio 5:7
Answers
Answer:
60:84
Step-by-step explanation:
We can divide 144 by 12 as 5+7 = 12.
We get 12 and we multiply 12 by both of the sections.
We get 60 and 84.
The cost of 3/4 kg onions is ₹ 21. One kg onions will cost .......
STEP BY STEP EXPLANATION NEEDED
PLS ANSWER I WILL MARK AS BRAINLIST
+10POINTS
Answers
Answer:
t
The cost of 34 kg onions=RS21
then,
the cost of 1kg onions=?
Now,
34kg=RS21
1kg=21÷34
1kg=0.61
hope it helps you!!
stay safe healthy and happy!!
Please help immediately!!

Answers
I desperately need help. PLEASE
*and please actually answer the question instead of lying just for points. seriously

Answers
check images :) and yeah i agree i hate when people just put random letters to get points




help me please number 8
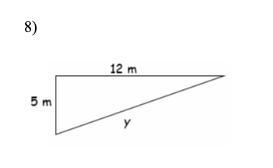
Answers
Answer:
13
Step-by-step explanation:
square root of 12^2 + 5^2
a person in a lighthouse 22m above sea level sights a buoy in the water. if the angle of depression to the buoy is 25o, how far from the base of the lighthouse is the buoy?
Answers
If the angle of depression to the buoy is 250, then the buoy is approximately 47.2 meters from the base of the lighthouse.
What is angle of depression ?
The angle of depression is the angle between a horizontal line of sight and the line of sight from an observer to a point or object that is lower than the observer. It is commonly used in trigonometry and geometry problems that involve the height or depth of an object relative to an observer or the ground.
We can start by drawing a diagram to visualize the situation.
In the diagram, A represents the location of the lighthouse, B represents the location of the buoy, and x represents the distance from the base of the lighthouse to the buoy that we want to find.
Since the angle of depression from the lighthouse to the buoy is 25 degrees, we know that angle ABx is also 25 degrees. We also know that the height of the lighthouse above sea level is 22 meters.
We can use the tangent function to find the value of x:
tan(25°) = opposite / adjacent
tan(25°) = 22 / x
Solving for x, we get:
x = 22 / tan(25°)
x ≈ 47.2 meters
Therefore, the buoy is approximately 47.2 meters from the base of the lighthouse.
Learn more about angle of depression click here:
https://brainly.com/question/17193804
#SPJ1

Can i get some help :

Answers
Answer: so, option 1 and 3 are true
1. True: The left side 6 is equal to the right side 6 , which means that the given statement is always true.
2. False: The left side 39 does not equal to the right side 9 , which means that the given statement is false.
3. True: The left side 16 is equal to the right side 16 , which means that the given statement is always true.
4. False: The left side 21 does not equal to the right side 19 , which means that the given statement is false.
Step-by-step explanation:
What i Limit of StartFraction x quared x minu 12 Over x quared minu 3 x EndFraction a x approache 3?
0
StartFraction 7 Over 3 EndFraction
4
DNE
Answers
The limit of the fraction as x approaches 3 is 4.
We can use algebraic manipulation to simplify the fraction.
StartFraction x squared minus 12 Over x squared minus 3 x EndFraction
= StartFraction x squared minus 12 Over x squared minus 3 x EndFraction x squared
= StartFraction x squared minus 12 x squared Over x squared times x squared minus 3 x EndFraction
= StartFraction x squared times x squared minus 12 x squared Over x squared times x squared minus 3 x EndFraction
= StartFraction x to the fourth minus 12 x squared Over x squared times x squared minus 3 x EndFraction
Now we can plug in x = 3 to get the limit:
= StartFraction 3 to the fourth minus 12 x 3 squared Over 3 squared times 3 squared minus 3 x EndFraction
= StartFraction 81 - 36 Over 27 - 9 EndFraction
= StartFraction 45 Over 18 EndFraction
= 4
Learn more about fraction here
https://brainly.com/question/10354322
#SPJ4
Determine which of the following equations have a graph whose y-coordinate of the y-intercept is positive? Select all that apply.

Answers
The equations that have y-coordinate of the y-intercept as positive is 3. h(x) = (x - 1)² and 5. b(x) = (x + 1)(x + 2).
What is y-intercept?The graph's intersection with the y-axis is known as the y-intercept. Finding the intercepts for any function with the formula y = f(x) is crucial when graphing the function. An intercept can be one of two different forms for a function. The x-intercept and the y-intercept are what they are. A function's intercept is the location on the axis where the function's graph crosses it.
The y-intercept is obtained when the x-coordinate is 0.
Thus, substitute the value of x = 0:
1. f(x) = x² + 3x - 2
f(x) = 0 + 3(0) - 2
f(x) = -2
False
2. g(x) = x² - 10x
g(x) = 0 - 10(0)
g(x) = 0
3. h(x) = (x - 1)²
h(x) = (0 - 1)²
h(x) = 1
True
4. m(x) = 5x² - 3x - 5
m(x) = 5(0) - 3(0) - 5
m(x) = -5
False
5. b(x) = (x + 1)(x + 2)
b(x) = (0 + 1)(0 + 2)
b(x) = 2
True
Hence, the equations that have y-coordinate of the y-intercept as positive is 3. h(x) = (x - 1)² and 5. b(x) = (x + 1)(x + 2).
Learn more about y-intercept here:
https://brainly.com/question/27395007
#SPJ1
What function call will generate a random number in the range of 1 through 6 using the random module
Answers
Both of these approaches will generate a random number in the range of 1 through 6 using the random module in Python.
To generate a random number in the range of 1 through 6 using the random module in Python, you can use the `randrange()` function or the `choice()` function from the random module. Here are examples of both approaches:
Using `randrange()`:
import random
random_number = random.randrange(1, 7)
In this example, `random.randrange(1, 7)` generates a random integer from 1 up to, but not including, 7. The `random_number` variable will store the randomly generated number.
Using `choice()`:
import random
random_number = random.choice(range(1, 7))
In this example, `range(1, 7)` creates a sequence of numbers from 1 to 6, and `random.choice()` randomly selects one element from that sequence. The `random_number` variable will store the randomly chosen number.
Both of these approaches will generate a random number in the range of 1 through 6 using the random module in Python.
To learn more about random numbers refer to:
brainly.com/question/13534392
#SPJ4
find the equation of the line that passes through (-3,5) and is perpendicular to the line passing through (-6,(1)/(2)) and (-4,(2)/(3))
Answers
The equation of the line that passes through (-3, 5) and is perpendicular to the line passing through (-6, 1/2) and (-4, 2/3) is y = -12x - 31.
To find the equation of the line that passes through (-3, 5) and is perpendicular to the line passing through (-6, 1/2) and (-4, 2/3), we need to follow these steps:
1. Find the slope of the given line.
2. Determine the negative reciprocal of the slope to find the slope of the perpendicular line.
3. Use the slope and the point (-3, 5) to find the equation of the perpendicular line using the point-slope form.
Let's begin by finding the slope of the given line:
Slope of the given line = (y2 - y1) / (x2 - x1)
= ((2/3) - (1/2)) / (-4 - (-6))
= ((4/6) - (3/6)) / (-4 + 6)
= (1/6) / 2
= 1/12
The slope of the given line is 1/12.
To find the slope of the perpendicular line, we take the negative reciprocal:
Slope of perpendicular line = -1 / (1/12)
= -12
The slope of the perpendicular line is -12.
Now, using the slope (-12) and the point (-3, 5), we can find the equation of the perpendicular line using the point-slope form:
y - y1 = m(x - x1)
Substituting the values, we get:
y - 5 = -12(x - (-3))
y - 5 = -12(x + 3)
y - 5 = -12x - 36
y = -12x - 36 + 5
y = -12x - 31
Therefore, the equation of the line that passes through (-3, 5) and is perpendicular to the line passing through (-6, 1/2) and (-4, 2/3) is y = -12x - 31.
Learn more about reciprocal:https://brainly.com/question/20896748
#SPJ11
Katalin drove 180 miles on her vacation. She drove an average of 1.5 times faster on the second 90 miles of her trip than she did on the first 90 miles of her trip. Which expression represents the time she spent driving? Let x = her speed on the first half of the trip.
Answers
===================================================
Work Shown:
x = speed on 1st half of the trip
distance = rate*time
90 = x*t
t = 90/x
She spent 90/x hours driving on the 1st half of the trip
1.5x = speed on the 2nd half of the trip
d = r*t
t = d/r
t = 90/(1.5x)
t = 60/x
She spent 60/x hours driving on the 2nd half of the trip
Overall, she spent 90/x+60/x hours driving the entire 180 mile trip.
Edit:
That expression simplifies to 150/x since 90+60 = 150
Social scientists gather data from samples instead of populations because
a. samples are much larger and more complete.
b. samples are more trustworthy.
c. populations are often too large to test.
d. samples are more meaningful and interesting
Answers
Social scientists gather data from samples instead of populations because c. populations are often too large to test.
Social scientists often cannot test an entire population due to its size, so they gather data from a smaller group or sample that is representative of the larger population. This allows them to make inferences about the larger population based on the data collected from the sample. The sample size must be large enough to accurately represent the population, but it is not necessarily larger or more complete than the population itself. Trustworthiness, meaning, and interest are subjective and do not necessarily determine why social scientists choose to gather data from samples.
To know more about Collection visit
https://brainly.com/question/31734526
#SPJ11
find the probability that the coin lands heads exactly 11 times. a. 0.1602 b. 0.5731 c. 0.2941 d. 0.1527 e. 0.6374
Answers
The probability of landing heads exactly 11 times when a coin is tossed 20 times is option a) 0.1602
The repeated tossing of a coin follows a binomial distribution
P(X = x) = ⁿCₓ pˣ (1 - p)⁽ⁿ ⁻ ˣ⁾
where,
n = No. of times the experiment was repeated
x = random variable defining the number of "successes"
p = probability of "success"
Here
"succeess" is the event of landing a head.
n = 20
x = no. of times heads should show, i.e 11
p = probability of landing a head in a single toss
= 1/2
Hence, putting all this in the formula above we get
P(X = 11) = ²⁰C₁₁ 0.5¹¹ (1 - 0.5)⁽²⁰ ⁻ ¹¹⁾
= ²⁰C₁₁ 0.5¹¹ 0.5⁹
= ²⁰C₁₁ 0.5²⁰
= 20!/ 11! (20 - 11)! X 0.5²⁰
= a) 0.1602
Complete Question
An unbiased coin is tossed 20 times.
Find the probability that the coin lands heads exactly 11 times
a. 0.1602
b. 0.5731
c. 0.2941
d. 0.1527
e. 0.6374
To learn more about probability visit
https://brainly.com/question/12844710
#SPJ4
it can be shown that y1=e3x and y2=e−7x are solutions to the differential equation y′′ 4y′−21y=0 on the interval (−[infinity],[infinity]). find the wronskian of y1,y2 (note the order matters)
Answers
The Wronskian of y1 = e^(3x) and y2 = e^(-7x) on the interval (-∞, ∞) is W(y1, y2) = 10.
To find the Wronskian of y1 = e^(3x) and y2 = e^(-7x), we can use the formula for calculating the Wronskian of two functions. Let's denote the Wronskian as W(y1, y2).
The formula for calculating the Wronskian of two functions y1(x) and y2(x) is given by:
W(y1, y2) = y1(x) * y2'(x) - y1'(x) * y2(x)
Let's calculate the derivatives of y1 and y2:
y1(x) = e^(3x)
y1'(x) = 3e^(3x)
y2(x) = e^(-7x)
y2'(x) = -7e^(-7x)
Now, substitute these values into the Wronskian formula:
W(y1, y2) = e^(3x) * (-7e^(-7x)) - (3e^(3x)) * e^(-7x)
= -7e^(3x - 7x) - 3e^(3x - 7x)
= -7e^(-4x) - 3e^(-4x)
= (-7 - 3)e^(-4x)
= -10e^(-4x)
So, the Wronskian of y1 = e^(3x) and y2 = e^(-7x) is W(y1, y2) = -10e^(-4x).
Note that the order of the functions matters in the Wronskian calculation. If we were to reverse the order and calculate W(y2, y1), the result would be the negative of the previous Wronskian:
W(y2, y1) = -W(y1, y2) = 10e^(-4x).
Since the Wronskian is a constant value regardless of the interval (-∞, ∞) in this case, we can evaluate it at any point. For simplicity, let's evaluate it at x = 0:
W(y1, y2) = 10e^(0)
= 10
Therefore, the Wronskian of y1 = e^(3x) and y2 = e^(-7x) on the interval (-∞, ∞) is W(y1, y2) = 10.
Learn more about interval here
https://brainly.com/question/30354015
#SPJ11
plsss help meeeeeeeee

Answers
Answer:
Solution Below.
Step-by-step explanation:
This question tests on the concept of angle properties.
From the question above, we can form up an equation:
x + 2x + (x + 30) = 180 (Sum of angles in a triangle)
Now, we can solve for x to find the angles of each side.
\(x + 2 x + x + 30 = 180 \\ 4x + 30 \\ 4x = 150 \\ x = 37.5\)
Now we can find the angles for each side:
x = 37.5
2x = 2 × 37.5 = 75
x + 30 = 37.5 + 30 = 67.5
Answer:
37.5, 75, and 67.5
Step-by-step explanation:
The angles of a triangle add up to 180 so everything inside is equal to 180.
180=x+2x+x+30, simplify
180=4x+30, subtract 30 on both sides
150=4x, divide 4 on each side
37.5=x
solve now knowing x
x= 37.5
x+30= 67.5
2x= 75
Water is building up in a bathtub, After 3 minutes there are 12 gallons of water and after 5
minutes, there are 24 gallons of water. What is the average rate which water is entering the
bathtub from t=3 to t=5 minutes?
Answers
Answer:
i think its 15 gallons of water if you do the math you can see it
Step-by-step explanation:
Which expression shows the prime factorization of 66? please i need help so bad its a test

Answers
Answer:
B
2 times 3 times 11
Step-by-step explanation:
Mr. Swanson needs new strings for his 19 violin students. Each violin has 4 strings. Strings are $2 each and come in sets of 4. Mr. Swanson decides to buy 2 sets of strings for each student.
Answers
Please help
A cereal box manufacturer changes the size of the box to increase the amount of cereal it contains. The expressions 15 + 7.6n and 11 + 8n, where n is the number of
smaller boxes, are both representative of the amount of cereal that the new larger box contains. How many smaller boxes equal the same amount of cereal in the large
box?
The larger box of cereal has as much cereal as
(Type a whole number.)
smaller boxes
Answers
Answer:
Step-by-step explanation:
A cereal box manufacturer changes the sizeof the box to increase the amount of cereal itcontains. The equations 12 + 7.6n and 6 + 8n,where n is the number of smaller boxes, areboth representative of the amount of cereal thatthe new larger box contains. How many smallerboxes equal the same amount of cereal in thelarger box?
How long will it take for a $3000 investment to grow to $6450 at an annual rate of 10%, compounded quarterly? Assume that no withdrawals are made. Do not round intermediate computations, and round your answer to the nearest hundreth
Answers
It will take approximately 4.1 years for a $3000 investment to grow to $6450 at an annual rate of 10%, compounded quarterly.
What is compound interest?The interest that is accrued on both the principle and any accumulated interest from earlier periods is known as compound interest. In other words, interest is gained on top of interest and is reinvested. With time, compound interest increases enormously.
Simple interest, on the other hand, is interest that is simply paid on the principle. As interest is not reinvested, the investment's growth is linear over time.
The compound interest is given by the formula:
\(A = P(1 + r/n)^{(nt)}\)
Substitute the values given:
\(A = $3000(1 + 0.10/4)^{(4t)}\\$6450 = $3000(1 + 0.10/4)^{(4t)}\\2.15 = (1 + 0.10/4)^{(4t)}\)
Taking log on both sides we have:
\(ln(2.15) = ln[(1 + 0.10/4)^{(4t)]}\)
ln(2.15) = 4t ln(1 + 0.10/4)
t = ln(2.15)/(4 ln(1 + 0.10/4))
t ≈ 4.1
Hence, it will take approximately 4.1 years for a $3000 investment to grow to $6450 at an annual rate of 10%, compounded quarterly.
Learn more about compound interest here:
https://brainly.com/question/29335425
#SPJ1
I taught my daughter to drive and she was a bit heavy on the brakes to start. During drives to and from her school, there are 16 locations requiring braking (e.g., roundabouts, stop signs, slip lanes etc.). Further, a school term has 50 days, meaning 100 total drives back and forth. Assume the wear on the brake pads from each braking instance has a mean of 0.009mm and standard deviation of 0.025mm.
a) If the lining of my brake pads is 16.5mm thick at the start of a term, what is the approximate chance they last out the term (assuming my daughter misses no days of school)? [2 marks]
b) In fact, wear is uneven between front and rear pads. Suppose total wear on the rear pads during a single trip is normal with mean 0.16mm and standard deviation 0.12mm, while total wear on the front pads is normal with mean 0.128mm and standard deviation 0.08mm. Further, assume the correlation between wear on the pads is 0.8. If the rear pad was worn down by 0.192mm during today’s morning drive, what is the probability the front pad wear was less than 0.16mm? [2 marks]
Answers
The chance that the brake pads last out the term can be calculated based on the probability that the total wear is less than or equal to 16.5mm - 0.144mm.
a) The chance that the brake pads last out the term can be approximated using the normal distribution. Since there are 16 locations requiring braking per round trip, the total wear per round trip can be modeled as a normal distribution with a mean of 16 * 0.009mm = 0.144mm and a standard deviation of 16 * 0.025mm = 0.4mm.
Therefore, the chance that the brake pads last out the term can be calculated based on the probability that the total wear is less than or equal to 16.5mm - 0.144mm.
To learn more about probability visit;
https://brainly.com/question/31828911
#SPJ11