Answers
It's an irrational number.
You can cross off terminating and repeating decimal so you're left with a rational or irrational number. A rational number is something that can be put into fraction form and/or have repeating or terminating decimals.
So our answer would be irrational.
Related Questions
suppose a batch of steel rods produced at a steel plant have a mean length of 164 millimeters, and a variance of 121. if 287 rods are sampled at random from the batch, what is the probability that the mean length of the sample rods would differ from the population mean by less than 0.56 millimeters? round your answer to four decimal places.
Answers
The probability that the mean length of the sample rods differs from the population mean by less than 0.56 millimeters is approximately 0.8051.
To solve this problem, we need to calculate the probability that the mean length of the sample rods differs from the population mean by less than 0.56 millimeters.
Given:
Population mean (μ) = 164 millimeters
Variance (σ²) = 121
Sample size (n) = 287
Standard deviation of the sample mean (σₘ) = σ / √n
First, let's calculate the standard deviation of the sample mean:
σₘ = √(σ² / n)
= √(121 / 287)
= √(0.4216)
= 0.6495 (rounded to four decimal places)
Next, we need to calculate the Z-score for the given difference of 0.56 millimeters:
Z = (difference from population mean) / σₘ
= 0.56 / 0.6495
= 0.8624
Using a standard normal distribution table or calculator, we can find the probability corresponding to this Z-score. The probability will be the area under the curve to the left of the Z-score.
Looking up the Z-score of 0.8624 in the standard normal distribution table, we find that the corresponding probability is approximately 0.8051.
Therefore, the probability that the mean length of the sample rods differs from the population mean by less than 0.56 millimeters is approximately 0.8051.
Learn more about probability here
https://brainly.com/question/31828911
#SPJ4
Q.2. Determine the Fourier Transform and Laplace Transform of the signals given below. • x(t) = e-³t u(t) • x(t) = e²t u(-t) • x(t) = e4t u(t) x(t) = e2t u(-t+1)
Answers
Let's determine the Fourier Transform and Laplace Transform for each of the given signals.
1. x(t) = e^(-3t)u(t)
Fourier Transform (X(ω)):
To find the Fourier Transform, we can directly apply the definition of the Fourier Transform:
X(ω) = ∫[from -∞ to +∞] x(t) * e^(-jωt) dt
Plugging in the given signal:
X(ω) = ∫[from 0 to +∞] e^(-3t) * e^(-jωt) dt
Simplifying:
X(ω) = ∫[from 0 to +∞] e^(-t(3+jω)) dt
Using the property of the Laplace Transform for e^(-at), where a = 3 + jω:
X(ω) = 1 / (3 + jω)
Laplace Transform (X(s)):
To find the Laplace Transform, we can use the property that the Laplace Transform of x(t) is equivalent to the Fourier Transform of x(t) multiplied by jω.
X(s) = jωX(ω) = jω / (3 + jω)
2. x(t) = e^(2t)u(-t)
Fourier Transform (X(ω)):
Using the definition of the Fourier Transform:
X(ω) = ∫[from -∞ to +∞] x(t) * e^(-jωt) dt
Plugging in the given signal:
X(ω) = ∫[from -∞ to 0] e^(2t) * e^(-jωt) dt
Simplifying:
X(ω) = ∫[from -∞ to 0] e^((-jω+2)t) dt
Using the property of the Laplace Transform for e^(-at), where a = -jω + 2:
X(ω) = 1 / (-jω + 2)
Laplace Transform (X(s)):
To find the Laplace Transform, we can use the property that the Laplace Transform of x(t) is equivalent to the Fourier Transform of x(t) evaluated at s = jω.
X(s) = X(jω) = 1 / (-s + 2)
3. x(t) = e^(4t)u(t)
Fourier Transform (X(ω)):
Using the definition of the Fourier Transform:
X(ω) = ∫[from -∞ to +∞] x(t) * e^(-jωt) dt
Plugging in the given signal:
X(ω) = ∫[from 0 to +∞] e^(4t) * e^(-jωt) dt
Simplifying:
X(ω) = ∫[from 0 to +∞] e^((4-jω)t) dt
Using the property of the Laplace Transform for e^(-at), where a = 4 - jω:
X(ω) = 1 / (4 - jω)
Laplace Transform (X(s)):
To find the Laplace Transform, we can use the property that the Laplace Transform of x(t) is equivalent to the Fourier Transform of x(t) evaluated at s = jω.
X(s) = X(jω) = 1 / (4 - s)
4. x(t) = e^(2t)u(-t+1)
Fourier Transform (X(ω)):
Using the definition of the Fourier Transform:
X(ω) = ∫[from -∞ to +
Visit here to learn more about Laplace Transform:
brainly.com/question/30759963
#SPJ11
WORTH 24 POINTS PLS HELP
On the blueprints for a new house, a wall measures 3.5 inches. If the map scale is 1.25 inches to 2 feet, how long will the actual wall be?
Answers
Answer:A unit rate is a comparison of two measurements, one of which has a value of ... The unit scale on a map may read \begin{align*}\frac{1}{2}\ inch=100 ... A line 4 inches long would represent an actual line of 800 feet. Unit scales and proportions can be used to calculate actual distances from maps, drawings, ...
Step-by-step explanation:
Which shows 71. 38 in word form? O A seventy-one thirty-eighths O B. Seventy-one and thirty eighths O c. Seventy-one and thirty-eight tenths D. Seventy-one and thirty-eight hundredths E seventy-one and thirty-eight thousands
Answers
The number 71.38 can be written in word form as "seventy-one and thirty-eight hundredths." The correct answer is option D.
In decimal notation, the number 71.38 can be broken down into its whole number and decimal parts. The whole number part is 71, and the decimal part is 0.38.
In a decimal number, the digits to the right of the decimal point represent fractions of a whole. Each digit to the right of the decimal point has a place value that is a power of 10.
In word form, the decimal part 0.38 is read as "thirty-eight hundredths." Therefore, when combined with the whole number 71, the correct word form is "Seventy-one and thirty-eight hundredths."
Therefore option D is the correct answer.
Learn more about the whole number:
https://brainly.com/question/9879870
#SPJ11
Evaluate the expression. -12 divided by 4 - 6
Answers

Answer:
-9
Step-by-step explanation:
Hope this helps.
which number is a factor of 100

Answers
Answer:
20
I hope this helps!
Answer:
20
Step-by-step explanation:
hope this helps I know I'm too late.
katie made a scale drawing of a house. the scale she used was 1 inch : 2 feet. in the drawing, a rug in the hallway is 4 inches long. what is the length of the actual rug?
Answers
The length of the actual rug is 8 feet
In the given statement is ,
Katie made a Scale drawing of a house. The scale she used was 1inch : 2 feet. In the drawing, a rug in the hallway is 4 inches long.
To find the length of the actual rug
Now, According to the question:
and, based on the given condition
We know that,
1 feet = 12 inches
2 feet = 24 inches
By using Multiplication Rule
4 x 24 = 96 inches
and, we convert inches into feet
Thus, 96 inches = 8 feet
Hence, The length of the actual rug is 8 feet
Learn more about Scale Drawing at:
https://brainly.com/question/24271603
#SPJ4
Write the slope intercept form of the equation of the line described:
Through (−1, 2 ), parallel to y= −x−1
Answers
Answer:
\(2 = - ( - 1) + b\)
\(b = 1\)
\(y = - x + 1\)
How long would it take R20000 invested today at a simple interest rate of 9% p.a. to reach an investment goal of R30000.
A Approximately 5.6 years
B Approximately 6.1 years
C Approximately 4.7 years
D Approximately 5.1 years
Answers
\(~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\dotfill & \$ 30000\\ P=\textit{original amount deposited}\dotfill & \$20000\\ r=rate\to 9\%\to \frac{9}{100}\dotfill &0.09\\ t=years \end{cases} \\\\\\ 30000 = 20000[1+(0.09)(t)] \implies \cfrac{30000}{20000}=1+0.09t\implies \cfrac{3}{2}=1+0.09t \\\\\\ \cfrac{3}{2}-1=0.09t\implies \cfrac{1}{2}=0.09t\implies \cfrac{1}{2(0.09)}=t\implies 5.6\approx t\)
Piper invested $4,700 in an account paying an interest rate of 4. 8% compounded continuously. Assuming no deposits or withdrawals are made, how much money, to the nearest cent, would be in the account after 19 years?.
Answers
Assuming no deposits or withdrawals are made, the amount in the account after 19 years is: 11,454. 133.
How to find the amount in the account?Using this formula
A = P(1+r/100)ⁿ
Where:
A = Amount =?
P = Principal = $4700
r = Interest rate =4.8%
n = the number of periods =19 years
Let plug in the formula
A = 4,700 (1 + 4.8/100)¹⁹
A = 4,700 (1 + 0.048)¹⁹
A = 4,700 (1.048)¹⁹
A = $11,454. 133
Therefore the amount is $11,454. 133.
Learn more about amount in the account here:https://brainly.com/question/14541900
#SPJ1
18 i
Use the given information to find the amount A in the account earning compound interest after 6 years when the principal is $3500.
r=1. 83%, compounded daily
Answers
When the principal is $3500 and the annual interest rate is 1.83%, compounded daily, the balance in the account receiving compound interest after 6 years is $4,036.32.
To find the amount A in the account earning compound interest after 6 years when the principal is $3500, we need to use the compound interest formula:
\(A = P(1 + \frac{r}{n})^{nt}\)
Where:
P = principal = $3500
r = annual interest rate = 1.83% = 0.0183 (as a decimal)
n = number of times the interest is compounded per year = 365 (daily compounding)
t = time in years = 6
Substituting these values into the formula, we get:
\(A = 3500(1 + \frac{0.0183}{365})^{(365*6)}\)
\(A = 3500(1.00005)^{2190}\)
A = $4,036.32
Therefore, the amount in the account earning compound interest after 6 years when the principal is $3500, with an annual interest rate of 1.83% compounded daily, is $4,036.32.
To learn more about compound interest refer to:
brainly.com/question/14295570
#SPJ4
The values in the table represent a function.
f(x)
8
X
-6
7
4
3
-5
3
-5
-2
12
Use the drop-down menus to complete the
statements.
The ordered pair given in the first row of the table can
be written using function notation as
f(3) is
◊
f(x) = -5 when x is
Done
Answers
The ordered pair given in the first row of the table can be written as (8, f(8)).
f(3) is equal to 7.
f(x) = -5 when x is -6 or -2.
The table represents a function where the input values (x) correspond to the output values (f(x)). Let's analyze the given information to complete the statements:
The ordered pair given in the first row of the table can be written using function notation as (x, f(x)) = (8, f(8)). This means that when x is equal to 8, the corresponding function value is f(8).
To find f(3), we look for the row in the table where x is equal to 3. From the given table, we can see that when x is 3, the corresponding function value f(x) is 7. Therefore, f(3) is equal to 7.
Similarly, to find when f(x) is equal to -5, we look for the rows in the table where the function value is -5. From the table, we can see that when x is equal to -6 and -2, the function value f(x) is -5. Therefore, we can say that f(x) = -5 when x is -6 or -2.
In summary:
The ordered pair given in the first row of the table can be written as (8, f(8)).
f(3) is equal to 7.
f(x) = -5 when x is -6 or -2.
for such more question on ordered pair
https://brainly.com/question/11661554
#SPJ8
Help plz I have time and I need to show work

Answers
Compare finding the slope using a table and graph
Answers
PLZ HELP I NEED THIS DONE TO PASS
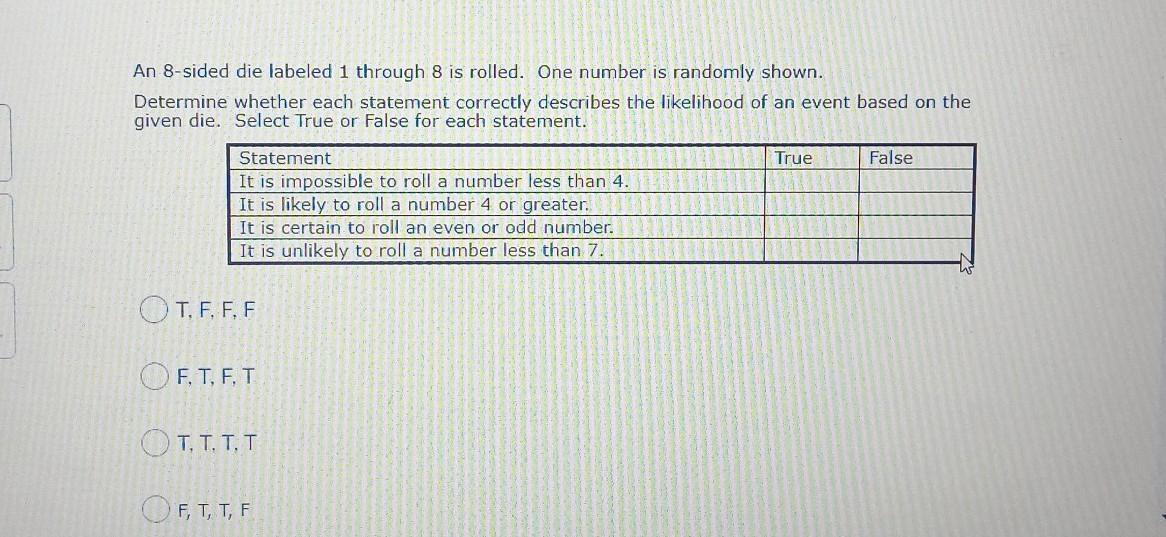
Answers
Answer:
F, T, T, F
Step-by-step explanation:
1) F because the die is labeled 1 through 8. Because 1 through 3 are included within the die, it is possible to roll a number less than 4.
2) T because the die is from 1 to 8, meaning 5 through 8 - number 4 and greater - are able to be rolled. Rolling a 4, 5, 6, 7, or 8, has a probability of 5/8 chance of being rolled, making it a likely roll (as 5/8 is over a 50% chance).
3) T as numbers are always either even or odd, meaning it is impossible not to roll an even or odd number. In other words, it is certain to roll an even or odd number.
4) F as it is extremely likely to roll a number less than 7 with a whopping 6/8 chance of being rolled. What would be unlikely is rolling a number greater than 7.
An infinite geometric series contains consecutive terms 262.4, 209.92, 167.963 and the sum is 1640. What is the first term?
Answers
Answer:
328
Step-by-step explanation:
\(\frac{a}{1-r}\) is the equation for the sum of an infinite geometric series, where \(a\) is the first term of the infinite geometric series, and r is the common ratio between the terms. Here, we can find the common ratio between any consecutive terms. \(\frac{209.92}{262.4} = \frac{4}{5}\)
Therefore, \(\frac{a}{1-\frac{4}{5}} = 1640\).
This simplifies to \(5a = 1640\)
Therefore, \(a = 328\)
there are 349 students at a college who have taken a course in calculus, 216 who have taken a course in discrete mathematics, and 188 who have taken courses in both calculus and discrete mathematics. how many students have taken a course in either calculus or discrete mathematics?
Answers
The students have take a course in either calculus or discrete mathematics are 377 students.
- Based on the condition, identify the variables:
Calculus = C
Discrete Math = D
- After that, formulated one by one:
There are 349 students in a college who have taken a course in calculus,
N(C) = 349
216 who have take a course in discrete mathematics,
N(D) = 216
188 who have taken a course in both of calculus and discrete mathematics.
N(C and D) = 188
- From information above, here the solution:
N(C or D) = N(C) + N(D) - N(C and D)
N(C or D) = 349 + 216 - 188
N(C or D) = 377
The students have take a course in either calculus or discrete mathematics are 377 students.
WORD MATH PROBLEM
Word math problems are written problems that involve solving a mathematical calculation based on a set of instructions that describe a "real-life" situation in only a few phrases.
If you follow these five simple procedures, you'll be able to solve any word math problem, here they are:
- Take your time reading the issue and getting a firm grasp on its nature.
- Use variables to represent data that is not known.
- Make the remaining part of the problem a mathematical expression.
- Put an end to this predicament.
- Verify your answers.
Learn more about word math problem here:
https://brainly.com/question/11240316
#SPJ4
Katerina's phone number has ten digits in total. Now her friend Kylie wants to call her, but Kylie only remembers the first six digits. How many times Kylie has to try at most in order to call Katerina if she does not dial repetitive phone numbers?
Answers
Kylie has to try at most 3,024 different combinations in order to call Katerina if she does not dial repetitive phone numbers.
Kylie only recalls the first six numbers of Katerina's phone number, so she must guess the last four. Because she cannot repeat any of the numbers she has already successfully predicted, the first remaining digit has just nine viable alternatives (all digits from 0 to 9 except the one she already knows). Similarly, the second remaining digit has just eight options, the third has seven, and the fourth has six.
Therefore, the total number of possible combinations is:
9 x 8 x 7 x 6 = 3,024
This implies Kylie will have to try at most 3,024 different combinations to reach Katerina, provided she gets it right on the last try.
Learn more about Combination:
https://brainly.com/question/30450879
#SPJ4
For a fundraiser, a school club is selling raffle tickets for $2 each and healthy snacks for $1.50 each. What is the total cost of y raffle tickets and x healthy snacks?
Answers
Answer:
1.5x+2y=total cost
Step-by-step explanation:
if x+y=10 and x-y=6 what is this value of x cube - y cube
Answers
Answer:
x cubed minus y cubed is equal to 504
Step-by-step explanation:
First we need to know what the values of x and y are. We can do this pretty easily, by just solving both equations for x, and equating them to each other:
With the first:
x + y = 10
x = 10 - y
And with the other
x - y = 6
x = 6 + y
Now that we have two definitions of x, we can say that the expressions are equal, and solve for y:
10 - y = 6 + y
10 - 6 = y + y
4 = 2y
y = 2
And now that we know what y is, we can find x:
x = 10 - y
x = 10 - 2
x = 8
So x is equal to eight. We can check our answer by plugging x into the other equation and seeing if we get the same value for y:
x - y = 6
8 - y = 6
-y = 6 - 8
-y = -2
y = 2
So we know we solved that correctly.
Now if we cube each number, eight cubed is equal to 512, and 2 cubed is equal to 8. If we subtract the latter from the former we get 504.
so x cubed minus y cubed is equal to 504
A circle has a diameter of 20 cm. Find the area of the circle, leaving
π in your answer.
Include units in your answer.
Answers
If circle has a diameter of 20 cm, the area of the circle is 100π square centimeters.
The area of a circle can be calculated using the formula:
A = πr²
where A is the area, π (pi) is a mathematical constant that represents the ratio of the circumference of a circle to its diameter (approximately 3.14), and r is the radius of the circle.
In this case, we are given the diameter of the circle, which is 20 cm. To find the radius, we can divide the diameter by 2:
r = d/2 = 20/2 = 10 cm
Now that we know the radius, we can substitute it into the formula for the area:
A = πr² = π(10)² = 100π
We leave π in the answer since the question specifies to do so.
It's important to include units in our answer to indicate the quantity being measured. In this case, the area is measured in square centimeters (cm²), which is a unit of area.
To learn more about area click on,
https://brainly.com/question/19784529
#SPJ1
How do you solve a system of linear equations using substitution or elimination?
Answers
Answer:
Refer to the step-by-step explanation. If you need any clarification on a part just add a comment under this answer :)
Step-by-step explanation:
Given a system of equations, there are a few methods to calculate solutions of that system. Two ways to do so are by using elimination or substitution.
To solve a set of equations by elimination you will take two equations and either add or subtract them to eliminate one of the variables. Here is a quick example...
\(\left \{ {{3x+y=5} \atop {2x-y=0}} \right.\)
If we were to add these equations together, we could eliminate the variable \(y\\\) to get an equation to solve for \(x\).
After adding these equations we get: \(5x=5\)
We then can solve the equation for \(x\\\), to find the value of \(x\), and use that value to plug back (a.k.a substitute) into the other equations to solve for \(y\)
To solve a set of equations by substitution you will take a system of equations, pick one of the equations and solve one of them for one variable. Here is a quick example...
\(\left \{ {{3x+2y=16} \atop {7x+y=19}} \right.\)
If we take the second equation and solve for the variable, \(y\), we will get an equation in terms of \(x\). We can then take that equation and plug it into the top, substituting \(y\), for the equation in terms of \(x\). Like so....
Solving bottom equation for \(y\), we get: \(y=19-7x\), now substitute this equation for \(y\) into the top equation.
We get: \(3x+2(19-7x)=16\), you now have an equation only in terms of \(x\), so you can solve for \(x\). I won't complete the whole problem but hopefully you get the idea :)
a hat company charges a design fee plus $4 per hat. the total cost of 5 hats is $30. how much will it cost for 3 hats?
Answers
Using Algebraic expression solution ,
The cost of three hats is $18 .
We have given that,
A hat company charge for design fee $4 per hat .
i.e design fee of one hat = $4
total cost of 5 hats = $30
let the cost of one hat without design fee be $x and total cost of one hat is $(x+4) .
using the above statement, we get an algebraic expression,
5( x+ 4)= 30
we solve the above algebra expression,
=> 5x + 20 = 30
=> 5x = 10
=> x = 2
so, cost of a hat without design fee is $2
and total cost of one hat is $6.
we have to calculate cost of 3 hats .
cost of one hat in hat company= $ 6
cost of three hats in hat company= $(6×3)
= $18
Hence, the total cost of 3 hats is $18.
To learn more about Algebraic expression , refer:
https://brainly.com/question/22763064
#SPJ4
use the remainder estimate for the integral test to find an upper bound for s − s100. compare this to the actual value of s − s100 (i.e., which is larger?).
Answers
Let's move to the solution of the problem you've asked about. To use the remainder estimate for the integral test to find an upper bound for s − s100, we need to use the following formula: Rn = sn - S`
Here, `Rn` = Remainder `sn` = The nth partial sum `S` = The actual value
We are required to find the upper bound for s − s100. We can write s − s100 as s - s1000 + s1000 - s100 By the integral test,
we have `s = int(1/(x(ln x)^p))dx ` Integrating it using u-substitution` u = ln x, du = dx/x` Substituting values,
`s = ∫du/(u^p)`= 1/(p-1)(u^(1-p)) + C = 1/(p-1)(ln x)^(1-p) + CAs p > 1, we have: `s < 1/(p-1)(ln x)^(1-p)` Therefore,
`s1000 < 1/(p-1)(ln 1000)^(1-p)`and`s100 < 1/(p-1)(ln 100)^(1-p)` Therefore, the upper bound of
`s - s100` is `R100 < s - s100 < R1000`. The actual value of `s - s100` is equal to `R1000`.Since `R1000 > R100`, the actual value of `s - s100` is larger than the upper bound. Therefore, the actual value is greater than the estimated value.
To find an upper bound for s - s100 using the remainder estimate for the integral test, follow these steps:
1. Determine the function f(x) that represents the given series. In this case, you didn't provide the series, so let's assume it's a general convergent series with a positive, continuous, and decreasing function f(x).
2. Apply the integral test to ensure the series converges. Since the function is positive, continuous, and decreasing, the integral test can be used.
3. Calculate the integral from 100 to infinity for f(x)dx, which will give you an upper bound for the error s - s100.
4. Compare this upper bound to the actual value of s - s100. If the actual value is smaller than the upper bound, the actual value is closer to the sum of the infinite series.
Visit here to learn more about upper bound:
brainly.com/question/1855715
#SPJ11
Which graph represents the function f(x) = -x-2?
Answers
The graph that represents the linear function -x - 2 is given by the image presented at the end of the answer.
How to graph the linear function?The linear function for this problem is defined as follows:
f(x) = -x - 2.
The x-intercept of the line is obtained when f(x) = 0, hence:
-x - 2 = 0
x = -2.
Meaning that the line passes through the point (-2,0).
The y-intercept of the line is obtained when x = 0, hence:
-0 - 2 = y
y = -2.
Meaning that the line passes through the point (0,-2).
Then the graph is made with a line connecting these two points.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1

Help me on this question please

Answers
The measure of angle DAB in the given quadrilateral can be calculated as: 109°.
How to Find the Measure of an Angle in a Quadrilateral?To find the measure of an angle in a quadrilateral, you need to use the fact that the sum of all angles in a quadrilateral is always equal to 360 degrees.
Using the above fact stated, we can add up the three known angles in the given quadrilateral and then subtract it from 360 degrees to find the measure of angle DAB.
Thus, we have:
m<DAB = 360 - (90 + 97 + 64)
m<DAB = 360 - 251
m<DAB = 109°
Learn more about Quadrilateral on:
https://brainly.com/question/30291770
#SPJ1
which expression is equivalent to 354x + 332, If x=0?
Answers
Answer:
10x + 332
when, x=0
Step-by-step explanation:
Please give me brainlist.
What is the solution for the system of linear equations shown in the graph? 3 3 2 2 2 DON 2 -3 a 7 7 3 N 3 4
I'll give brainiest to first answer if its correct pleass

Answers
The solution is given by the point of intersection of the two lines which is (-1/4, 3/4).
To find the point of intersection of two lines, we need to determine the equations of the lines and then solve them simultaneously.
Finding the equation of the first line passing through the points (-1, 3) and (0, 0).
The slope of the line (m1) can be calculated using the formula:
m1 = (y2 - y1) / (x2 - x1)
Substituting the values (-1, 3) and (0, 0):
m1 = (0 - 3) / (0 - (-1))
= -3 / 1
= -3
Using the point-slope form of the line equation:
y - y1 = m1(x - x1)
Substituting the values (-1, 3):
y - 3 = -3(x - (-1))
y - 3 = -3(x + 1)
y - 3 = -3x - 3
y = -3x
So, the equation of the first line is y = -3x.
Similarly, second line,
The slope of the line (m2) is:
m2 = (2 - 0) / (1 - (-1))
= 2 / 2
= 1
Using the point-slope form with the values (-1, 0):
y - 0 = 1(x - (-1))
y = x + 1
So, the equation of the second line is y = x + 1.
Equating the equations of the lines to find the point of intersection and hence the solution,
-3x = x + 1
0 = 4x + 1
-1 = 4x
x = -1/4
Put x = -1/4 in 2nd equation,
y = x + 1
y = (-1/4) + 1
y = 3/4
Therefore, the point of intersection of the two lines is (-1/4, 3/4).
Learn more about equation of a line click;
https://brainly.com/question/21511618
#SPJ1
what is the converse of the conditional statement? if x is even, then x 1 is odd. if x is not even, then x 1 is not odd. if x 1 is odd, then x is even. if x 1 is not odd, then x is not even. if x is even, then x 1 is not odd.
Answers
Conversing the conditional statement we get the answer as, if x is odd, then x+ 1 is even.
What is conversing the conditional statement?Two pieces make up a conditional statement: an assumption in the "if" clause and a conclusion in the "then" clause. Conversing, changes the hypothesis and conclusion to create the conditional statement's opposite.
The converse of the first conditional statement is:
If x is odd, then x + 1 is even.
If x is not odd, then x + 1 is not even.
If x + 1 is even, then x is odd.
If x + 1 is not even, then x is not odd.
Hence, in converse of the conditional statement we switch the hypothesis and the conclusion of the statements.
Learn more about conditional statement here:
https://brainly.com/question/18152035
#SPJ4
20 points! Find the equation of the linear function represented by the table below in slope-intercept form.
y = ___?___

Answers
The equation of the linear function is y =4x + 8
How to determin the equation of the linear functionFrom the question, we have the following parameters that can be used in our computation:
The table of values
A linear equation is represented as
y = mx + c
Where
c = y when x = 0
This means that
y = mx + 8
From the table, we have
A unit increment in x gives an increment of 4 in y
This means that
m = 4
So, we have
y = 4x + 8
Read more about equation at
https://brainly.com/question/2030026
#SPJ1
