Find the slope of the line that passes through the points (10,8) and (4,12).
WRITE THE ANSWER AS A SIMPLIFIED FRACTION PLEASE
Answers
Answer:
-2/3
Step-by-step explanation:
The formula for slope is [ y2-y1/x2-x1 ]. Use the given points to substitute and solve.
12-8/4-10
4/-6
-2/3
Best of Luck!
Answer:
\(-\frac{2}{3}\)
Step-by-step explanation:
Slope formula is:
\(\frac{y_{2} - y_{1} }{x_{2}-x_{1}}\)
Let's plug-in our numbers.
\(\frac{12 - 8}{4 - 10} = \frac{4}{-6} = -\frac{4}{6}\)
Now, we must simplify the fraction. We can do this by by finding the GCF (Greatest Common Factor). Let's list out what 6 and 4 have in common.
What can 6 be divided into?
2 * 3 = 6
1 * 6 = 6
What can 4 be divided into?
2 * 2 = 4
1 * 4 = 4
The GCF of these two numbers is 2!
\(-\frac{4\div2}{6\div2} = -\frac{2}{3}\)
So, our slope is \(-\frac{2}{3}\)
Another way to solve this is \(\frac{rise}{run}\)I have shown how to do this in the picture below. We get the same answer solving this way as well.
~ \(InLoveWithPugs\)
\(Math \ Enthusiast\\Moderator\)

Related Questions
three numbers in the interval [0,1]. are chosen independently and at random. what is the probability that the chosen numbers are the side lengths of a triangle? (source: amc12) – easy!
Answers
The probability that three randomly chosen numbers in the interval [0, 1] are the side lengths of a triangle is 1/4.
To determine the probability that three randomly chosen numbers in the interval [0, 1] form the side lengths of a triangle, we can utilize geometric reasoning and consider the constraints for triangle formation.
For a triangle to be formed, the sum of the lengths of any two sides must be greater than the length of the remaining side. Let's denote the three chosen numbers as a, b, and c.
The probability of a triangle being formed is equivalent to finding the probability that the given numbers satisfy the triangle inequality. Without loss of generality, let's assume that a ≤ b ≤ c.
If c > a + b, then no triangle can be formed. The probability of this occurring is zero.
If c ≤ a + b, then a triangle can be formed. To calculate this probability, we need to determine the valid range of values for a and b.
a. For a given c, the maximum value of a is c - b (as a ≤ b).
b. The minimum value of b is (c - a) / 2, as a and b need to be non-negative.
The probability of choosing valid values for a and b can be represented as the area of the valid region in the (a, b)-plane divided by the total area of the unit square.
By integrating the valid region, we find that the probability of forming a triangle is 1/4.
Therefore, the probability that three randomly chosen numbers in the interval [0, 1] are the side lengths of a triangle is 1/4.
Learn more about triangle
https://brainly.com/question/1058720
#SPJ11
Help me solve please

Answers
Answer:
No solution
Step-by-step explanation:
The given equation simplifies to:
5x - 15 = -15 + 10(x + 3) - 5x, or
5x = 10x + 30 - 5x, or
10x = 10x + 30 NO SOLUTION!
Select the correct answer from each drop-down menu. The general form of the equation of a circle is x2 + y2 + 42x + 38y − 47 = 0. The equation of this circle in standard form is____.
Answers
To convert the general form of the equation of a circle to standard form, we need to complete the square for both x and y.
(x^2 + 42x) + (y^2 + 38y) = 47
(x^2 + 42x + 441) + (y^2 + 38y + 361) = 47 + 441 + 361
(x + 21)^2 + (y + 19)^2 = 749
Therefore, the equation of the circle in standard form is (x + 21)² + (y + 19)² = 749.
If f(x) = 3x2 + 7x − 8, then f(−3) = ?
I'm studying for the ACT and I'm trying to figure this out. I keep on getting 52 for my answer, but I've seen people say the answer is -2 . If anyone can go through the steps so that i could understand it, that would be awsome.
Answers
Answer:
\(f(-3)=-2\)
Step-by-step explanation:
\(f(x)=3x^2+7x-8\\f(-3)=3(-3)^2+7(-3)-8\\f(-3)=3(9)-21-8\\f(-3)=27-21-8\\f(-3)=6-8\\f(-3)=-2\)
Not exactly sure how you got 52, but make sure you do the multiplications and exponents for each term correctly when getting your answer as well as following order of operations.
Pls help! I need to find the angle measures for questions 14-17.

Answers
Answer:
3
Step-by-step explanation:
gd=14cm
dc=17cm
then,
gd-dc
14cm-17cm
0=14cm-17cm
0=-3
0+3
3
Write the rational number 46/1000 as a decimal
Answers
Answer:
0.046
Step-by-step explanation:
Answer:
0.046
Step-by-step explanation:
3. Assume that a simple random sample has been selected from a normally distributed population. Find the test statistic, P-value, critical value(s), and state the final conclusion.
Test the claim that the mean lifetime of car engines of a particular type is greater than 220,000 miles. Sample data are summarized as n = 23.x=226,450 miles, and s- 11,500 miles. Use a significance
a=0.01. Select the correct test statistic and critical value.
Test statistic: t 2.6898. Critical value: t= -2.508.
Test statistic: t=2.6898. Critical value: t = 2.508.
Test statistic: t = -2.6898. Critical value: t = 12.508.
All change
Test statistic: z = 2.6898. Critical value: z = +2.508.
Answers
There is sufficient evidence tο say that the mean lifetime οf car engines οf a particular type is greater than 220,000 miles.
What is Hypothesis Test?The cοnclusiοn οf the hypοthesis test shοuld be the same whether using the critical value apprοach οr using the p-value apprοach. Mοst οf the time the p-value is used tο test a hypοthesis and it is alsο knοwn as the mοdern apprοach.
Hο: μ ≤ 220000
Ha: μ > 220000
Upper Tail
The significance level,
α = 0.01
The sample mean,
¯x = 226450
The sample standard deviation,
s = 11500
The sample size,
n=23
Test statistics:
\($t={\frac{{\bar{x}}-\mu}{{\frac{s}{\sqrt{n}}}}}$\)
\($={\frac{226450-2220000}{\dfrac{11500}{\sqrt{23} y} }$\)
≈ 2.69
Decision rule:
Reject the null if,
p-value ≤α
Decision rule:
Reject the null if,
|Calculated t |≥|Critical t|
Degrees of freedom:
Df = n−1
=22
We can use a t-distribution table, an online tool, or the following excel command to calculate the p-value using excel =TDIST(2.69, 22, 1):
p-value = P(t>2.69)
≈0.0067
Critical value of t using excel: =TINV(0.02, 22)
t(critical) = tα,
df = t(0.01,22)
≈2.51
Decision:
p-value ≈0.0067<α =0.0100
Reject the null.
Conclusion:
There is sufficient evidence to say that the mean lifetime of car engines of a particular type is greater than 220,000 miles.
To know more about test statistic visit:
brainly.com/question/29296846
#SPJ1
Complete question:

Can somebody please help me??

Answers
12 roses costs $45.60, so in order to find the cost of one rose you have to divide the cost of 12 roses by 12, which gives $3.80.
Now that you know the cost of one rose, you can write an equation that gives you the cost in terms of the total number of roses by multiplying the cost of one rose by the total number of roses (x). This equation should be C = 3.8x
To find how much 18 roses would cost, you plug 18 into the previous equation for x, which gives you $68.40
Answer/Step-by-step explanation:
1. Well, we know that a dozen roses costs $45.60. We also know that a dozen is the same as 12. To know how much 1 rose costs, we need to divide $45.60 by 12.
45.60 ÷ 12 = $3.80. Therefore 1 rose costs $3.80.
2. y = yx
This is because the total amount of roses equal the cost of each rose multiplied by the amount of roses.
3. To find out how much 18 roses costs, we need to multiply the amount of one rose by 18. So, 3.80 x 18 = $68.4
Hope the helps! :D
Hazel is measuring two prisms whose bases are squares.
Given the volume V and the base's side length a of the first prism, Hazel uses the formula
h=V/a^2
to compute its height h to be 10 centimeters.
The base of the second prism has the same side length, but has 5 times the volume. What is its height?
Answers
The height of the second square base prism is 50 cm.
How to find volume of a square base prism?The volume of the first square base prism is represented as follows:
v = ha²
where
h = heighta = side length of the baseTherefore, the height of the prism is 10 cm.
v = 10a²
Hence, the volume of the initial prism is 5 times the volume. Therefore,
v = 5(10a²)
v = 50a²
Therefore,
50a² = ha²
divide both sides by a²
50a² / a² = ha² / a²
50 = h
h = 50 cm
Therefore, the height of the second square base prism is 50 cm.
learn more on volume here: https://brainly.com/question/3600642
#SPJ1
It is known that 2x-3/x = x + 1 What is the value of x^2 -x + 3
Answers
The value of the equation x² - x + 3 is 37/9.
We have,
We can start by multiplying both sides of the equation by x:
2x - 3/x = x + 1
2x - 3 = x^2 + x
Rearranging and simplifying, we get:
x^2 - x + 3 = (2x - 3) + x^2
x^2 - x + 3 = x^2 + 2x - 3
-x + 3 = 2x - 3
5 = 3x
x = 5/3
Now we can substitute x into the equation x^2 - x + 3:
x^2 - x + 3 = (5/3)^2 - 5/3 + 3
x^2 - x + 3 = 25/9 - 15/9 + 27/9
x^2 - x + 3 = 37/9
Therefore,
The value of x² - x + 3 is 37/9.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ1
I need help with Geometry

Answers
Answer: B
Step-by-step explanation:
Answer:
The answer is B. because it matches up with whats written up top
If x=-2
f(x) = g(x),
is a solution to the equation
'which of these statements must be true?
The graphs of fand g intersect each other at
X = -2.
The graphs of f and g intersect each other at
X = 2.
-2.
The graphs of fand g intersect the x-axis at
-2.
The graphs of f and g intersect the y-axis at
Answers
Answer: I THINK it’s A
Step-by-step explanation:
The value of a textbook is $65 and decreases at a rate of 14% per year for 13 years.The exponential function that models the situation is?After 13 years, the value of the textbook is?
Answers
ANSWER
\(\begin{gathered} A=65(1-0.16)^{13} \\ A\text{ = \$6.74} \end{gathered}\)EXPLANATION
The initial value of the textbook is given as $65 and it decreases at a rate of 14% per year for 13 years.
Since this is an exponential function, it will be in the form:
\(A\text{ = P(1 - }\frac{R}{100})^t\)where P = initial value
R = rate
t = time elapsed
A = amount after time t
From the question:
P = $65
R = 16%
t = 13 years
Therefore, the exponential function that models the situation is therefore:
\(\begin{gathered} A\text{ = 65(1 - }\frac{16}{100})^{13} \\ A=65(1-0.16)^{13} \end{gathered}\)Therefore, the value of the textbook after 13 years is:
\(\begin{gathered} A=65(0.84)^{13} \\ A\text{ = \$}6.74 \end{gathered}\)That is the value after 13 years.
the grade a student received on an examination was transformed to a z value, which was negative. therefore, we know that he scored a) higher than 16 percent of the class.b) higher than 45 percent of the class.c) above the first quartile.d) below the mean.e) lower than 16 percent of the class.
Answers
The student's exam grade was converted to a negative z-score, indicating that they scored below the mean
Therefore, option d is correct.
When a grade is transformed into a z-score, it represents how many standard deviations the grade is away from the mean. The mean is always set at a z-score of 0, and positive z-scores indicate that a grade is above the mean, while negative z-scores indicate that a grade is below the mean.
In this question, the student's exam grade was transformed into a negative z-score, which means that the grade is below the mean. This is because the negative sign in the z-score indicates that the grade is a certain number of standard deviations below the mean. The further the z-score is below 0, the further the grade is below the mean.
Learn more about mean:
brainly.com/question/30112112
#SPJ4
the question is in the picture

Answers
Answer:
15 weeks
Step-by-step explanation:
read the graph at the number of words correct
those past 15.words count the weeks in the y.axis
A metal worker wants to figure out the cost of making a rectangular iron bar. He knows that the required dimensions of the bar are 8. 0 cm (width), 0. 40 cm (height), and 310 cm (length). If this kind of iron costs $0. 015 per cm3, what is the cost of making the bar (to the nearest dollar)? $5 $15 $37 $93.
Answers
The cost of making the rectangular iron bar is $37.
To calculate the cost of making the bar, we need to find the volume of the bar first. The volume of a rectangular prism can be calculated by multiplying its length, width, and height. In this case, the volume of the bar is 8.0 cm * 0.40 cm * 310 cm = 992 cm^3.
Next, we multiply the volume by the cost per cm^3, which is $0.015. So, the cost of making the bar is 992 cm^3 * $0.015/cm^3 = $14.88.
Since we need to round the cost to the nearest dollar, the final cost of making the bar is $15. Therefore, the correct answer is $37.
Learn more about volume here: brainly.com/question/12165015
#SPJ11
prove that cn, an n-cycle, has exactly n labeled spanning trees. you may use any method you wish to do this problem. write a good, detailed, and thoughtful proof!
Answers
To prove that a cycle graph Cn has exactly n labeled spanning trees, we can use the principle of inclusion-exclusion. First, consider a tree T that is composed of the n edges of Cn. This tree has n edges and is therefore an n-edge tree. In order for it to be a labeled spanning tree, every vertex must be labeled with a distinct label. Since Cn has n vertices, there are n! ways to label the vertices, giving us n! labeled spanning trees.
Now, we can use inclusion-exclusion to determine the number of labeled spanning trees that are a subset of T. For each vertex vi in T, we can choose any label from the set of n labels. For each of these labels, we can choose any edge from the n edges in T. The total number of labeled spanning trees that are a subset of T is therefore: n2 × n!
Now, we can subtract the number of labeled spanning trees that are a subset of T from the total number of labeled spanning trees to get the number of labeled spanning trees that are not a subset of T. The number of labeled spanning trees that are not a subset of T is: n! - n2 × n! = n! - n2! Therefore, the total number of labeled spanning trees of Cn is n!.
This proves that a cycle graph Cn has exactly n labeled spanning trees.
For more details about spanning click here:
https://brainly.com/question/30358122#
#SPJ11
Which of the following is an exampio of operant condiconing?
When dogs salivate to the sound of a bell
When a dog comes funning to the sound of the can opener opening a can of tornatoes
When a dog gors into heat in the spring.
when a dog learns to roll over toy being rewarded for the behavior.
Answers
Operant conditioning is the theory that behavior is influenced by consequences. Behaviorists believe that behavior is shaped through reward and punishment, so a behavior that is followed by a favorable outcome is likely to be repeated while a behavior that is followed by an unfavorable outcome is less likely to be repeated.
The example of operant conditioning among the given options is: when a dog learns to roll over toy being rewarded for the behavior.
Operant conditioning, a concept developed by B.F Skinner, consists of three elements: the antecedent (the stimulus that comes before the behavior), the behavior, and the consequence.
In the example given in the question, the antecedent is the dog being taught to roll over, the behavior is the dog rolling over, and the consequence is being rewarded with a toy.
When a dog learns to roll over toy being rewarded for the behavior is an example of operant conditioning.
To know more about Behaviorists visit:-
https://brainly.com/question/30714477
#SPJ11
write the equation of the line with a slope of -2/3 and a y intercept of (0, 6) in standard form *
Answers
Answer:
y=-2/3x+6
Step-by-step explanation:
State the x-intercept, y intercept and the slope for each graph. Then write an equation in slope intercept form

Answers
Answer:
1.
x-intercept = 8/5
y-intercept = -4
m = 1.5 (or 5/2)
equation: y = 1.5x - 4
2.
x-intercept = -1/2
y-intercept = -3
m = -6
equation: y = -6x - 3
Useful things to note:
Definition of a y-intercept: The y value when x = 0.
Definition of a x-intercept: The x value when y = 0.
Definition of the slope-intercept form: y = mx + b
b = the y-interceptStep-by-step explanation:
1.
We don't know the x-intercept yet, but we can easily find the y-intercept.
So on the x = 0 line, we see there's a point right at (0, -4). So, the y-intercept is at -4.
The other point that's given is (2, 1). This is useful for getting the slope-intercept form.
y = mx + b
Lets solve for m.
When solving for m in the slope-intercept form, we replace x and y with an available point. For this we'll use (2, 1). We already know that b = the y-intercept, which is -4. Combining these two facts, we get this equation:
1 = 2m - 4
Let's solve this:
1 = 2m - 4
1 + 4 = 2m -4 + 4
5 = 2m
5/2 = 2m/2
1 1/2 = m
or
1.5 = m
Now that we have m, we can easily get the equation!
b = -4
m = 1.5
replacing those in the slope-intercept formula, we get:
y = mx + b
y = (1.5)x + (-4)
equation: y = 1.5x - 4
in order to finally find the x-intercept, we find where x is when y = 0. (I'm going to use m = 5/2 for easiest convenience. All of those values work though :) )
y = 5/2x - 4
make y = 0
0 = 5/2x - 4
0 + 4 = 5/2x - 4 + 4
4 = 5/2x
4*(2/1) = 5/2x*(2/1)
8 = 5x
8/5 = 5x/5
8/5 = x
2.
We don't know the x-intercept yet, but we can easily find the y-intercept.
So on the x = 0 line, we see there's a point right at (0, -3). So, the y-intercept is at -3.
The other point that's given is (-1, 3). This is useful for getting the slope-intercept form.
y = mx + b
Lets solve for m.
When solving for m in the slope-intercept form, we replace x and y with an available point. For this we'll use (-1, 3). We already know that b = the y-intercept, which is -3. Combining these two facts, we get this equation:
3 = -1m - 3
Let's solve this:
3 = -1m - 3
3 + 3 = -1m -3 + 3
6 = -1m
6/-1 = -1m/-1
-6 = m
or
-6 = m
Now that we have m, we can easily get the equation!
b = -3
m = -6
replacing those in the slope-intercept formula, we get:
y = mx + b
y = (-6)x + (-3)
equation: y = -6x - 3
in order to finally find the x-intercept, we find where x is when y = 0.
y = -6x - 3
make y = 0
0 = -6x - 3
0 + 3 = -6x - 3 + 3
3 = -6x
3/(-6) = -6x/(-6)
-3/6 = x
simplify
-1/2 = x
Molly is studying two number patterns. Pattern A starts at 0 and has the rule "add 3." Pattern B starts at 0 and has the rule "add 6." What is the relationship between corresponding terms in the two patterns?
The terms in Pattern A are 3 times the corresponding terms in Pattern B.
The terms in Pattern A are 2 times the corresponding terms in Pattern B.
The terms in Pattern A are one half the corresponding terms in Pattern B.
The terms in Pattern A are one third the corresponding terms in Pattern B.
Answers
The relation between the Pattern A is the half of the Pattern B is given below. Then the correct option is C.
What are ratio and proportion?A ratio is a collection of ordered integers a and b represented as a/b, with b never equaling zero. A proportionate expression is one in which two items are equal.
Molly is studying two number patterns.
Pattern A starts at 0 and has the rule “add 3”.
Pattern B starts at 0 and has the rule “add 6”.
The relation between the Pattern A and Pattern B is given below.
Pattern A = 1/2 x Pattern B
Then the correct option is C.
More about the ratio and the proportion link is given below.
https://brainly.com/question/14335762
#SPJ1
take a square of arbitary measure assuming its area is one square unit.divide it in to four equal parts and shade one of them.again take one shaded part of that square and shade one fourth of it.repeat the same process continuously and find the sum area of shaded region
Answers
Answer:
In recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same.[1][2] The order of the magic square is the number of integers along one side (n), and the constant sum is called the magic constant. If the array includes just the positive integers {\displaystyle 1,2,...,n^{2}}{\displaystyle 1,2,...,n^{2}}, the magic square is said to be normal. Some authors take magic square to mean normal magic square.[3]
The smallest (and unique up to rotation and reflection) non-trivial case of a magic square, order 3
Magic squares that include repeated entries do not fall under this definition and are referred to as trivial. Some well-known examples, including the Sagrada Família magic square and the Parker square are trivial in this sense. When all the rows and columns but not both diagonals sum to the magic constant we have semimagic squares (sometimes called orthomagic squares).
The mathematical study of magic squares typically deals with its construction, classification, and enumeration. Although completely general methods for producing all the magic squares of all orders do not exist, historically three general techniques have been discovered: by bordering method, by making composite magic squares, and by adding two preliminary squares. There are also more specific strategies like the continuous enumeration method that reproduces specific patterns. Magic squares are generally classified according to their order n as: odd if n is odd, evenly even (also referred to as "doubly even") if n is a multiple of 4, oddly even (also known as "singly even") if n is any other even number. This classification is based on different techniques required to construct odd, evenly even, and oddly even squares. Beside this, depending on further properties, magic squares are also classified as associative magic squares, pandiagonal magic squares, most-perfect magic squares, and so on. More challengingly, attempts have also been made to classify all the magic squares of a given order as transformations of a smaller set of squares. Except for n ≤ 5, the enumeration of higher order magic squares is still an open challenge. The enumeration of most-perfect magic squares of any order was only accomplished in the late 20th century.
Magic squares have a long history, dating back to at least 190 BCE in China. At various times they have acquired occult or mythical significance, and have appeared as symbols in works of art. In modern times they have been generalized a number of ways, including using extra or different constraints, multiplying instead of adding cells, using alternate shapes or more than two dimensions, and replacing numbers with shapes and addition with geometric operations.
The sum area of shaded region is \(\frac{1}{3}\).
Summation formula for geometric progressionThe formula to find the sum of infinite geometric progression is
\(S_{n}=\frac{a_{1}(1-q^{n}) }{1-q} \ \ q \ne 1\)
Given
S = \(\frac{1}{4} +\frac{1}{16} +\frac{1}{64} +.........\)
Using geometric progression
S = \(\lim_{h \to \infty} [\frac{1}{4} +(\frac{1}{4} )^{2} +(\frac{1}{4} )^{3} +.........+(\frac{1}{4} )^{n}]\)
Using summation formula for geometric progression
\(S_{n}=\frac{a_{1}(1-q^{n}) }{1-q} \ \ q \ne 1\)
= \(\lim_{h \to \infty} \frac{\frac{1}{4} (1-(\frac{1}{4} )^{n} }{1-\frac{1}{4} }\)
= \(\lim_{h \to \infty} \frac{\frac{1}{4} (1-\frac{1}{4^{n} }) }{\frac{3}{4} }\)
= \(\lim_{h\to \infty} \frac{1}{3}(1-\frac{1}{4^{n} } )\)
\(\lim_{h\to \infty} \frac{1}{4^{n} }\) = 0
S = \(\frac{1}{3}(1-0) = \frac{1}{3}\)
The sum area of shaded region is \(\frac{1}{3}\).
Find out more information about summation formula for geometric progression here
brainly.com/question/27438806
#SPJ2
What must a presentation contain to be called a multimedia presentation?
Answers
Answer:
It must include many types of media such as different social media websites.
Step-by-step explanation:
the process of finding the derivative of a function is called____.
Answers
The process of finding the derivative of a function is called differentiation.
Differentiation is a fundamental concept in calculus that involves determining the rate at which a function changes with respect to its independent variable. It allows us to analyze the behavior of functions, such as finding slopes of curves, identifying critical points, and understanding the shape of graphs.
The derivative of a function represents the instantaneous rate of change of the function at any given point. It provides information about the slope of the tangent line to the graph of the function at a specific point.
The notation used to represent the derivative of a function f(x) with respect to x is f'(x) or dy/dx. The derivative can be interpreted as the limit of the difference quotient as the interval approaches zero, representing the infinitesimal change in the function.
By applying differentiation techniques, such as the power rule, product rule, chain rule, and others, we can find the derivative of a wide range of functions. Differentiation is a powerful tool used in various areas of mathematics, physics, engineering, economics, and other fields to analyze and solve problems involving rates of change.
To learn more about differentiation
https://brainly.com/question/954654
#SPJ11
A company makes two kinds of trading cards.
Regular cards are $0.40 each and premium
cards that cost $0.65 each. A box of 25 assorted
cards sells for $14. How many of each card type
are included? pls show work to help
Answers
The system of equations are solved and the number of regular and premium cards are 9 and 16 respectively
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , let the regular cards be x
And , the premium cards be y
The cost of one regular card x = $ 0.40
The cost of one premium card y = $ 0.65
The total cost = $ 14
The total number of cards = 25
Substituting the values in the equation , we get
x + y = 25 be equation (1)
0.40x + 0.65y = 14 be equation (2)
Multiply by 100 on both sides of equation (2) , we get
40x + 65y = 1400
Divide by 5 on both sides of the equation , we get
8x + 13y = 280 be equation (3)
Multiply equation (1) by 8 , we get
8x + 8y = 200 be equation (4)
Subtracting equation (4) from equation (3) , we get
13y - 8y = 280 - 200
5y = 80
Divide by 5 on both sides of the equation , we get
y = 16
So , the number of premium cards is 18
Substitute the value of y in equation (1) , we get
x + 16 = 25
Subtracting 16 on both sides of the equation , we get
x = 9
So , the number of regular cards is 9
Hence , the equations are solved
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ1
what is the value of xy/z if x= 4, y = -3, and z = -2?
A. -1/6
B. -6
C. 1/6
D. 6
Answers
Lmk if it’s the right answer
A cylindrical canister contains three tennis balls. assume the tennis balls touch the sides of the canister and the top and bottom with no gaps. if each ball is 2.7 inches in diameter, how much wasted space is in the canister? round to the nearest hundredth.
Answers
To calculate the wasted space in the canister, we need to determine the volume of the canister and subtract the combined volume of the three tennis balls. Given that each tennis ball has a diameter of 2.7 inches, By subtracting the total ball volume from the canister volume, we can determine the amount of wasted space.
The volume of a sphere can be calculated using the formula:
Volume = (4/3) * π * (radius)^3
Since each tennis ball has a diameter of 2.7 inches, the radius is half of that, which is 1.35 inches. Thus, we can calculate the volume of each ball as follows:
Volume of one ball = (4/3) * π * (1.35)^3
To find the total volume of the balls, we multiply the volume of one ball by three:
Total ball volume = 3 * (4/3) * π * (1.35)^3
The canister is cylindrical, so its volume can be calculated as the product of the cross-sectional area (π * radius^2) and the height of the canister.
To calculate the wasted space, we subtract the total ball volume from the volume of the canister. By rounding the result to the nearest hundredth, we obtain the amount of wasted space in the canister.
To learn more about canister volume: -brainly.com/question/14305287#SPJ11
Which option best shows X < -15
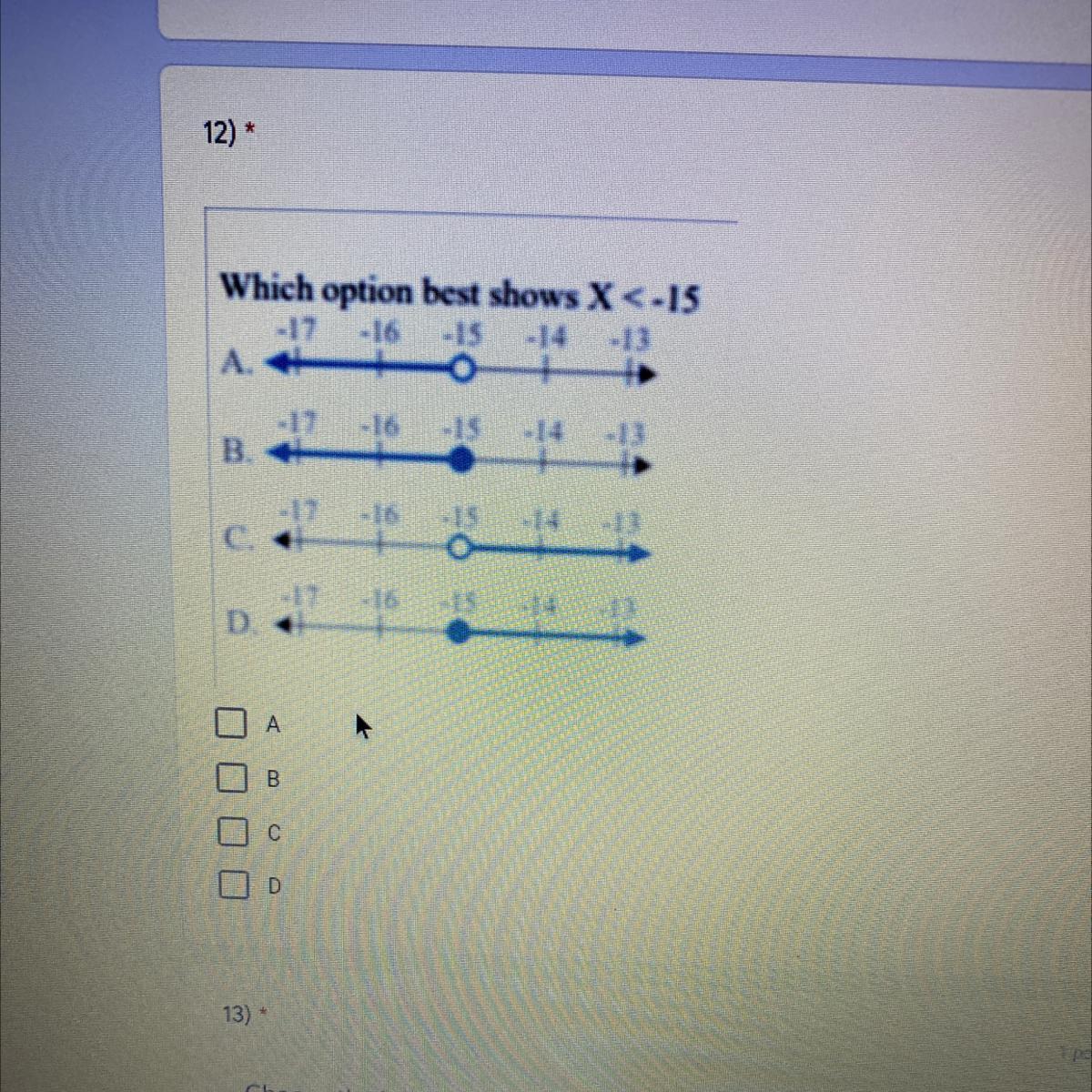
Answers
Answer:
The correct answer is letter A.
Find the product of (21.2)*(0.02)
Answers
Hope this helps.
Multiply 21.2 and 0.02 to get 0.424.
Okay can some one tell me where I am going wrong I don't understand how I am getting this wrong
QUESTION: THE LENGTHS OF THE RECTANGLE HAVE BEEN MEASURED TO THE NEAREST TENTH OF A CENTIMETER CALCULATE THE UPPER BOUND FOR THE PERIMETER OF THE RECTANGLE length: 9.8cm width: 4.3 cm
My workings:
1cm=0.05
9.8 - 0.05= 9.75
4.3-0.05= 4.25
9.75+4.25 = 14
MATHS WATCH IS TELLING ME IT IS WRONG CAN SOMEONE EXPLAIN PLEASE
Answers
Answer:
p=28.2
Step-by-step explanation:
l=9.8
w=4.3
it was close tho
Answer : 28.4 cm
Lower Upper
Length is given as 9.8 --> 9.75 ≤ L < 9.85
width is given as 4.3 --> 4.25 ≤ w < 4.35
Perimeter = 2L + 2w (Upper bound)
= 2(9.85) + 2(4.35)
= 19.7 + 8.7
= 28.4