Find the slope of (11,13), (18,4)
Answers
Answer:
-9or
Step-by-step explanation:
im not sure, i reccomend using a slope calculator
Related Questions
The local bank has a single line for customers waiting for the next available bank teller. There are four bank tellers who work at the same rate. The arrival rate of customers follows a Poisson distribution, while the service time follows an exponential distribution. Customers arrive at the bank at a rate of about twelve every hour. On average, it takes about 15 minutes to serve each customer. Answers to 2 d.p's.
(a) Calculate the probability that the bank is empty.
(b) Calculate the average time the customer spends waiting to be called.
(c) Calculate the average number of customers in in the bank.
(d) The average number of customers waiting to be served
Answers
a) The probability that the bank is empty is approximately 0.0026.
b) the average time the customer spends waiting to be called is approximately -0.25 c) hours the average number of customers in the bank is -1.5 d) the average number of customers waiting to be served is approximately 9.
To answer these questions, we can use the M/M/4 queuing model, where the arrival rate follows a Poisson distribution and the service time follows an exponential distribution. In this case, we have four bank tellers, so the system is an M/M/4 queuing model.
Given information:
Arrival rate (λ) = 12 customers per hour
Service rate (μ) = 1 customer every 15 minutes (or 4 customers per hour)
(a) To calculate the probability that the bank is empty, we need to find the probability of having zero customers in the system. In an M/M/4 queuing model, the probability of having zero customers is given by:
P = (1 - ρ) / (1 + 4ρ + 10ρ² + 20ρ³)
where ρ is the traffic intensity, calculated as ρ = λ / (4 * μ).
ρ = (12 customers/hour) / (4 customers/hour/teller) = 3
Substituting ρ = 3 into the formula, we have:
P = (1 - 3) / (1 + 4 * 3 + 10 * 3² + 20 * 3³) ≈ 0.0026
Therefore, the probability that the bank is empty is approximately 0.0026.
(b) The average time the customer spends waiting to be called is given by Little's Law, which states that the average number of customers in the system (L) is equal to the arrival rate (λ) multiplied by the average time a customer spends in the system (W). In this case, we want to find W.
L = λ * W
W = L / λ
Since the average number of customers in the system (L) is given by L = ρ / (1 - ρ), we can substitute this into the equation to find W:
W = L / λ = (ρ / (1 - ρ)) / λ
W = (3 / (1 - 3)) / 12 ≈ -0.25
Therefore, the average time the customer spends waiting to be called is approximately -0.25 hours, which is not a meaningful result. It seems there might be an error in the given data.
(c) The average number of customers in the bank (L) can be calculated as:
L = ρ / (1 - ρ) = 3 / (1 - 3) = -1.5
Therefore, the average number of customers in the bank is -1.5, which is not a meaningful result. It further suggests an error in the given data.
(d) The average number of customers waiting to be served can be calculated as:
\(L_q\) = (ρ² / (1 - ρ)) * (4 - ρ)
Substituting ρ = 3, we have:
\(L_q\\\) = (3² / (1 - 3)) * (4 - 3) ≈ 9
Therefore, the average number of customers waiting to be served is approximately 9.
For more about probability:
brainly.com/question/31828911
#SPJ4
Solve the following formula for the indicated variable.P = a + b + c; solve for b
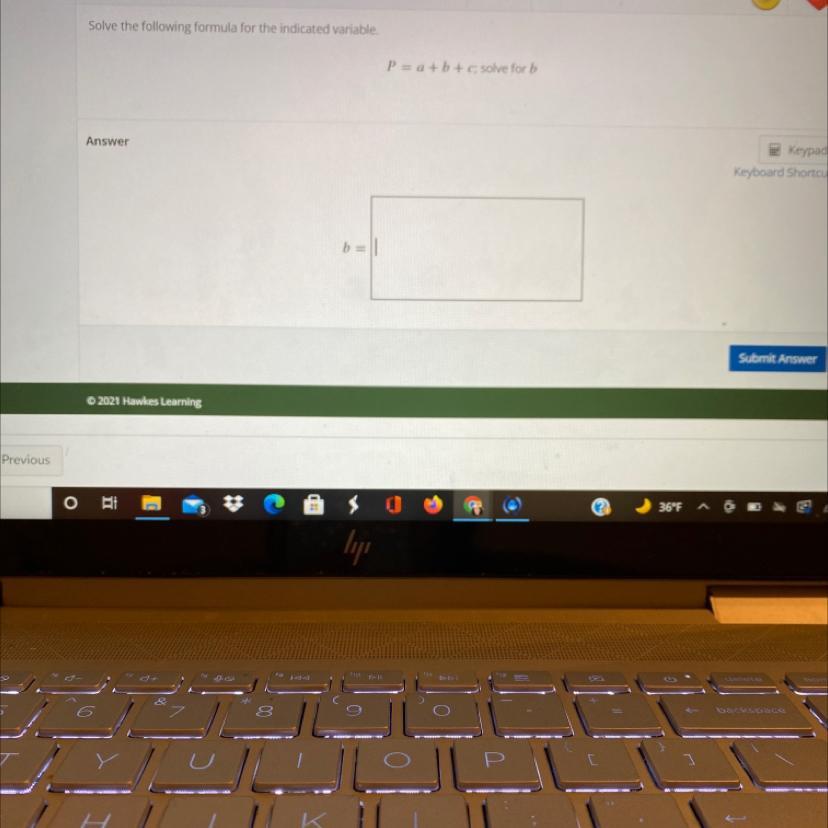
Answers
SOLUTION:
Step 1:
In this question, we are given the following:
Step 2:
Now, we are given the following:
\(\text{P = a+b + c}\)We are to solve for b, which means that we are to make b the subject of the formulae:
Step 3:
Now, solving for b, we have that:
\(b\text{ = P - a - c}\)h

3
Which statement is correct?
A
B
C
Four students each made a solid figure out of unit cubes. The table shows how many unit
cubes each student used.
D
Student
Austin
Maya
Colin
Sienna
Number of Unit
Cubes Used
28
24
36
32
The volume of Maya's figure is less than the volume of Austin's figure.
The volume of Colin's figure is less than the volume of Sienna's figure.
The volume of Austin's figure is greater than the volume of Colin's figure.
The volume of Maya's figure is greater than the volume of Sienna's figure.
Answers
Answer: a b c
Step-by-step explanation: a b c
ay you should help me with this tyty

Answers
Answer:
C. \(m=20\), \(n=10\)
Step-by-step explanation:
Since the triangle is a special 30°-60°-90° triangle, the hypotenuse is twice the size of the shortest leg. The long leg is \(\sqrt{3}\) of the short leg.
Select the correct answer.
An image of a rectangle of twenty-eight feet in length and sixteen feet in width. A rectangle is highlighted at fourteen feet long and eight feet wide. A right-angle triangle is formed below the rectangle. Text reads: reserved section and lawn.
The city mayor wants to use the reserved section of a rectangular park for gardening lessons conducted by the city public school. The rest of the park will be turned into a lawn. What will the area of the lawn be?
A.
168 square feet
B.
224 square feet
C.
280 square feet
D.
448 square feet
Answers
The 280 square foot lawn is in the designated area of a rectangular park that the city mayor wishes to use for gardening.
By area, what do you mean?An object's area is how much space it takes up in two-dimensions. It is the measurement of the quantity of unit squares that completely cover the surface of a closed figure.
The square-unit, which is frequently expressed as square inches, square feet, etc., is the accepted unit of area.
The rectangular park's allocated area is intended to be used by the city's public school for gardening courses.
The remaining area of the park will be developed into a lawn.
What is the lawn's formula?
The lawn's area is equal to the sum of its triangular and rectangle areas.
Lawn Area = 14 × 16 +.5 × 8 × 14
A = 224 + 56
A = 280 Ft²
Therefore, the correct option is 280ft² which is option C.
To know more about area, visit:
brainly.com/question/3948796
#SPJ1
Suppose y varies directly with x and y=76 when x=19 what is the value of x when y = "-32
Answers
The value of y = -32 , x = -8 .
What is the meaning of Direct Variation ?Direct Variation is when a variable is dependent on the other variable such that , on increasing one variable the other also increases.
It is given that
x and y are two variables
and they are in direct variation
y ∝ x
y = k x
where , k is the proportionality constant
From the given data , y = 76 when x = 19
76 = k * 19
k = 4
The value of x , when y = -32
-32 = 4 * x
x = -8
Therefore for y = -32 , x = -8 .
To know more about Direct Variation
https://brainly.com/question/14254277
#SPJ1
Find the reference angle of - 30°.
a) 270°
b) 180°
c) 300
d) 330
Answers
Answer:
Step-by-step explanation:
5ffg
-14/2 is = to what number my brain is saying no to math today.
Answers
Answer:
the answer would have to be -7
|12|____|-12| greater than or less than
Answers
Answer:
Step-by-step explanation:
>
Answer:
none of the above, its equal to
Step-by-step explanation:
|12|=|-12|
the absolute value of 12 is equal to the absolute value of -12
hope it helps have a great time learning!
- 45 × 47 solve using distributive property
Answers
Answer: -2115
Step-by-step explanation:
We can use the distributive property to simplify the calculation of -45 × 47 as follows:
\(\huge \boxed{\begin{minipage}{4 cm}\begin{align*}-45 \times 47 &= -45 \times (40 + 7) \\&= (-45 \times 40) + (-45 \times 7) \\&= -1800 - 315 \\&= -2115\end{align*}\end{minipage}}\)
Refer to the attachment below for explanation
Therefore, -45 × 47 = -2115 when using the distributive property.
________________________________________________________

To solve this problem using the distributive property, we can break down -45 into -40 and -5. Then we can distribute each of these terms to 47 and add the products:
\(\begin{aligned}-45 \times 47 &= (-40 - 5) \times 47 \\ &= (-40 \times 47) + (-5 \times 47) \\ &= -1{,}880 - 235 \\ &= \boxed{-2{,}115}\end{aligned}\)
\(\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}\)
For this experiment you have been randomly assigned to a group consisting of you and one other person. You do not know now, nor will you ever know, who this other person is. For this experiment all you have to do is distribute your 10 points into two accounts. One account called KEEP and one account called GIVE. The GIVE account is a group account between you and your group member. For every point that you (or your group member) put in the GIVE account, I will add to it 50% more points and then redistribute these points evenly to you and your group member. The sum of the points you put in KEEP and GIVE must equal the total 10 points. Any points you put in the KEEP account are kept by you and are part of your score on this experiment. Your score on the experiment is the sum of the points from your KEEP account and any amount you get from the GIVE account. For example, suppose that two people are grouped together. Person A and Person B. If A designates 5 points in KEEP and 5 points in GIVE and person B designates 10 points to KEEP and 0 points to GIVE then each person’s experiment grade is calculated in this manner: Person A’s experiment grade = (A’s KEEP) + 1.5(Sum of the two GIVE accounts)/2 = 5 +(1.5)(0+5)/2= 5 + 3.75 = 8.75. Person A’s score then is 8.75 out of 10. Person B’s experiment grade = (B’s KEEP) + 1.5(Sum of the two GIVE accounts)/2 = 10 +(1.5)(0+5)/2 = 10 + 3.75. Person B’s score then is 13.75 out of 10. (you can think of any points over 10 as extra credit) In this module’s activity you were asked to make a decision about how to invest your resources (points). This activity is a classic strategic game where the good of the individual is at odds with the good for the group. These problems are pervasive in risk management. For example, a physician who is trained to treat diseases may be reluctant to discuss alternative treatments with a patient when the physician is sure that a specific treatment is the only truly viable treatment. Nonetheless, you have learned in this course that physicians (or an agent of the physician) must have this discussion and bow to the will of the patient even if, in the physician’s judgment, the patient chooses an alternative treatment which is likely to be superfluous. In this way, informed consent and patient education are nuisances to the physician but are very important to protect the group (maybe a hospital or surgical group) from liability. In light of recent events another example is warranted. Individuals may choose to not get vaccinated since they do not want to bear the risk of any possible adverse side-effects of a vaccine. This is perfectly reasonable to do so. The problem arises when large groups of people choose to not get vaccinated thus making the impact of the disease relatively larger than need be if everyone would choose to take a vaccine (remember our first cost-benefit experiment). This implies that individual’s rights to choose not to vaccinate are at odds with what is good for the group of individuals. These types of problems are common in risk management. Discussion: (If you post your answers to each of the four questions below before the deadline, you will get the full ten points for the discussion. The questions do not need to be answered mathematically or with a calculation. If you feel the need to use mathematics to make a calculation, then you are free to do so but the questions are merely asking you for a number and how you arrived at that number. If you do not do any calculations to arrive at the number, just say how you arrived at the number. (There are no incorrect answers.) 1. In this activity how did you arrive at your decision on the keep-give split? 2. What is the best outcome of this situation for you? 3. What is the best outcome of this situation for the group? 4. Can you see any parallels with this game and how risk management strategies work? Explain.
Answers
1. I based my decision on allocating points to maximize my own score, while also considering the potential benefits of contributing to the group fund.
2. The best outcome for me would be allocating the minimum points required to the GIVE account, while putting the majority in the KEEP account. This would ensure I receive the most points for myself.
3. The best outcome for the group would be if both participants maximized their contributions to the GIVE account. This would create the largest group fund, resulting in the most redistributed points and highest average score.
4. There are parallels with risk management strategies. Individuals may act in their own self-interest, but a larger group benefit could be achieved if more participants contributed to "group" risk management strategies like vaccination, safety protocols, insurance policies, etc. However, some individuals may free ride on others' contributions while benefiting from the overall results. Incentivizing group participation can help align individual and group interests.
The given planes intersect in a line. Find parametric equations for the line of intersection. [Hint: The line of intersection consists of all points (x, y, z) that satisfy both equations. Solve the system and designate the unconstrained variable as t .]
x + 2y + z = 1, 2x+5y + 32 = 4
Answers
The parametric equations for the line of intersection are:
x = 61 - 5t
y = 2t - 30
z = t
To find the parametric equations for the line of intersection of the given planes, we first need to solve the system of equations:
1. x + 2y + z = 1
2. 2x + 5y + 32 = 4
Step 1: Solve for x from equation 1:
x = 1 - 2y - z
Step 2: Substitute x in equation 2 with the expression found in step 1:
2(1 - 2y - z) + 5y + 32 = 4
Now we can use elimination to solve for one variable. Let's eliminate y by multiplying the first equation by 5 and subtracting it from the second equation:
Step 3: Simplify and solve for y:
2 - 4y - 2z + 5y + 32 = 4
y - 2z = -30
Step 4: Designate z as the parameter t:
z = t
Step 5: Substitute z with t in the expression for y:
y = 2t - 30
Step 6: Substitute z with t in the expression for x:
x = 1 - 2(2t - 30) - t
x = 1 - 4t + 60 - t
x = 61 - 5t
Now we have the parametric equations for the line of intersection:
x = 61 - 5t
y = 2t - 30
z = t
Note that we can choose any value of z for the parameter t, since z is unconstrained.
Learn more about Parametric:
brainly.com/question/15585522
#SPJ11
question show in the photo, don’t mind the answer in the text box

Answers
From the problem, we have the formula :
\(T=2\pi rh+2\pi r^2\)Solving for h in terms of T and r will be :
\(\begin{gathered} T=2\pi rh+2\pi r^2 \\ T-2\pi r^2=2\pi rh \\ \frac{T-2\pi r^2}{2\pi r}=h \\ \frac{T}{2\pi r}-r=h \end{gathered}\)The answer is :
\(h=\frac{T}{2\pi r}-r\)Using p′=0.167, q′=0.833, and n=180, what is the 95% confidence interval for the proportion of the population who prefer brand named items?
Answers
The 95% confidence interval for the proportion of the population who prefer brand named items is:
CI = (0.102, 0.232)
What is confidence interval?
A confidence interval is a statistical tool used to estimate the range of possible values in which a population parameter, such as the mean or proportion, is expected to lie with a certain level of confidence based on the observed sample data.
To find the 95% confidence interval for the population proportion, we use the formula:
CI = p′ ± z*\(\sqrt{(p'q'/n)\)
where:
CI: confidence interval
p′: sample proportion
q′: 1 - p′
z: z-score from the standard normal distribution for the desired confidence level (95% in this case)
n: sample size
Substituting the given values, we get:
CI = 0.167 ± 1.96\(\sqrt{((0.1670.833)/180)\)
Simplifying, we get:
CI = 0.167 ± 0.065
Therefore, the 95% confidence interval for the proportion of the population who prefer brand named items is:
CI = (0.102, 0.232)
This means that we can be 95% confident that the true population proportion of people who prefer brand named items falls within this range.
To learn more about confidence interval visit:
https://brainly.com/question/15712887
#SPJ4
Simplify, Write your answer in exponential notation.
a.) 2³ x 2-5
b.) (602)3
Answers
The simplified expressions are 2^-2 and 60^6
How to simplify the expressions?Expression (a)
We have:
2^3 * 2^-5
Apply the product law of indices
2^3 * 2^-5 = 2^(3 - 5)
Evaluate the difference
2^3 * 2^-5 = 2^-2
Expression (b)
We have:
(60^2)^3
Apply the power law of indices
(60^2)^3 = 60^(2 * 3)
Evaluate the product
(60^2)^3 = 60^6
Hence, the simplified expressions are 2^-2 and 60^6
Read more about expressions at:
https://brainly.com/question/723406
#SPJ1
complete the proof, word bank at bottom
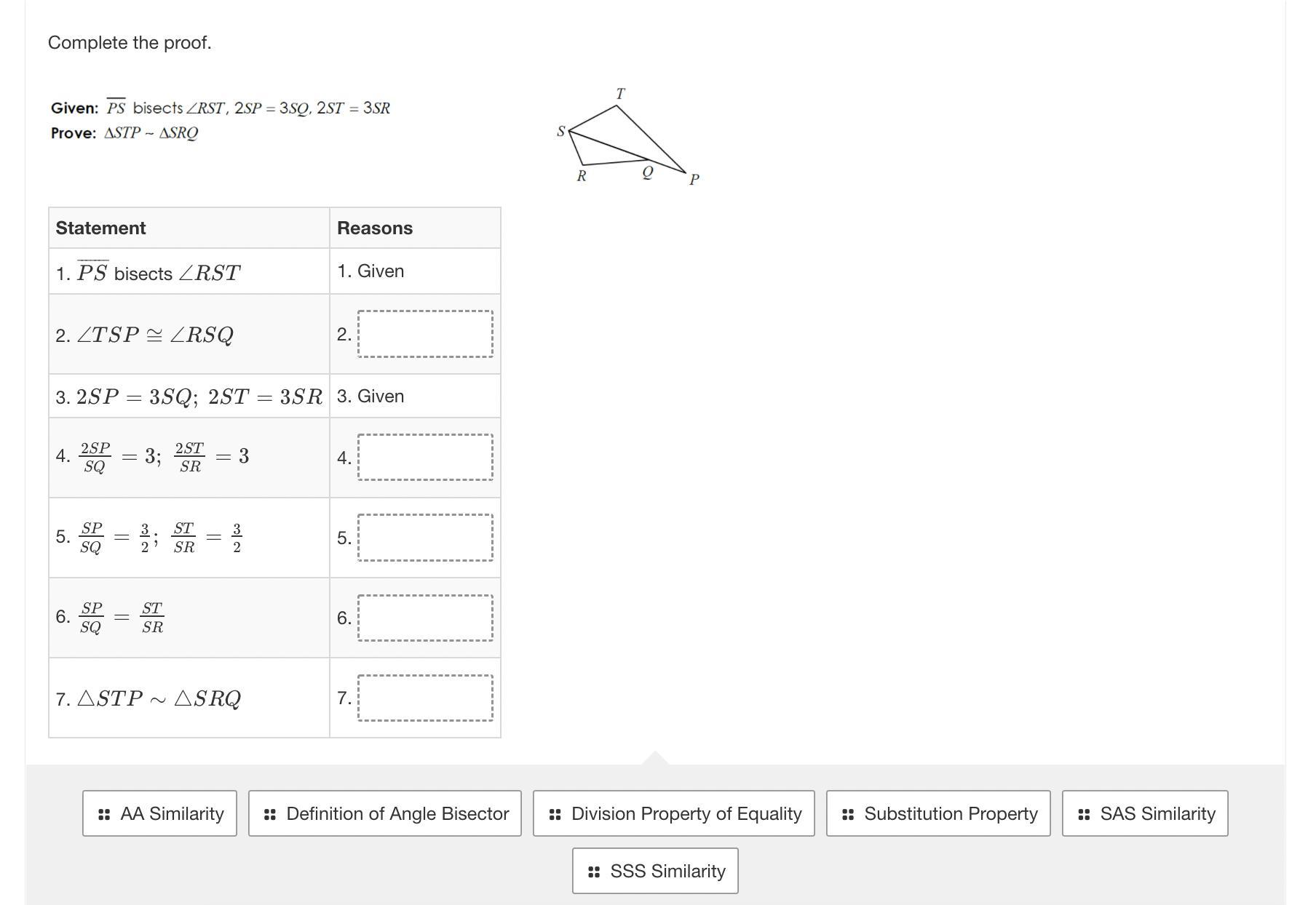
Answers
Answer:
Step-by-step explanation:
2) definition of angle bisector
4) division property of equality
5) division property of equality
6) substitution property
7) SAS similarity
in an figure lines BC||PQ , if angle ABP=150*,Find the angle DCQ

Answers
Answer:
i cant understand bief it plz
Step-by-step explanation:
Marks
2x + 3y = 53
3x - y = 19
Work out the values of x and y.
Answers
Answer:
2x+3y=53eq1
3x-y=19eq2
or,-y=19-3x
or,y=19-3x
keeping value of y in eq 1
2x+3y=53
or,2x+3(3x-19)
or2x+19-57=53
or,11x=53+57
or,11x=110
or,x=110\11
=10
againputting the value of x in eq1
2x+3y=53
or,20+3Y=53
or,3y=53-20
or,y=33\3
or,Y=11
At the p.e. class, pupils help each other measure heights. the average height of jeremy and justin is 147 cm. jeremy is 24 cm taller than justin. what is the height of jeremy?
Answers
The height of Jeremy is 159 cm.
What is average?In layman's terms, an average is a single number chosen to represent a set of numbers, typically the sum of the numbers divided by the number of numbers in the set (the arithmetic mean). The average of the numbers 2, 3, 4, 7, and 9 (summed to 25) is 5, for example. An average could be another statistic, such as the median or mode, depending on the context.To find the height of Jeremy:
The formula of average = sum of terms/number of termsLet, Justin, be x and Jeremy be x + 24So,
147 = x + (x+24) / 22x + 24 = 147 × 22x + 24 = 2942x = 294 - 242x = 270x = 135Then, Jeremy = 135 + 24 = 159 cm.
Therefore, the height of Jeremy is 159 cm.
Know more about average here:
https://brainly.com/question/20118982
#SPJ4
A) These polygons are similar. Determine the values of x° and y°.

Answers
Y= 64
They’re similar which means they’re enlarged so therefore the angles are unaffected
he line y =-x passes through the origin in the xy-plane, what is the measure of the angle that the line makes with the positive x-axis?
Answers
The line y = -x, passing through the origin in the xy-plane, forms a 45-degree angle with the positive x-axis.
The slope-intercept form of a linear equation is y = mx + b, where m represents the slope of the line. In this case, the equation y = -x has a slope of -1. The slope indicates the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line.
To determine the angle between the line and the positive x-axis, we need to find the angle that the line's slope makes with the x-axis. Since the slope is -1, the line rises 1 unit for every 1 unit it runs. This means the line forms a 45-degree angle with the x-axis.
The angle can also be determined using trigonometry. The slope of the line (-1) is equal to the tangent of the angle formed with the x-axis. Therefore, we can take the inverse tangent (arctan) of -1 to find the angle. The arctan(-1) is -45 degrees or -π/4 radians. However, since the line is in the positive x-axis direction, the angle is conventionally expressed as 45 degrees or π/4 radians.
Learn more about angle here:
https://brainly.com/question/31818999
#SPJ11
1
To find the quotient of 8- 3. multiply 8 by
1
8
o
1
3
03.
08.

Answers
to divide by a fraction, you multiply by the reciprocal which just means reversing the fraction. so 8/ 1/3 is the same as 8 x 3.
the conditions that the sum of forces and the sum of the torques both vanish:
Answers
Answer and Explanation: The conditions when the net force and the net torque are zero are called static equilibrium.
Help me…………………..999:7

Answers
You need to first add the 2 fullest containers. These are 4.5 and 4.5. Once we add them, we get 9 liters of milk. Then, we must divide them into 3 equal parts. This means we do 9/3 to get an answer of 3 L per milk container.
It seems the problem was cut off a little so let me know if this doesn't work.
Find the volume of each sphere to the nearest hundredth?
Answers
Answer:
Can i have a diagram please
Step-by-step explanation:
problem 3.7. suppose integer polynomials p and q satisfy that p ( x)/ q ( x ) is an integer for infinitely many integer inputs x. does it follow that q ( x ) divides p ( x ) ?
Answers
Integer polynomials p and q fulfill that for an unlimited number of inputs of integers x, p (x)/q (x) is an integer. q (x) does not necessarily divide p. (x)
Sums of terms of the form k^xn, where k is any number and n is a positive integer, make up polynomials. For instance, the polynomial 3x+2x-5. a description of polynomials.This section covers the ideas of degree, standard form, monomial, binomial, and trinomial.
Learn more about polynomials here
https://brainly.com/question/11536910
#SPJ4
Work out the value of angle x.
X
62°
Answers
Step-by-step explanation:
the question is not clear
(0)
Which equation shows an example of the associative property of addition? (-7+i)+7i=-7+(i+7i) (-7+i)+7i=7i+(-7i+i) 7i*(-7i+i)=(7i-7i)+(7i*i) (-7i+i)+0=(-7i+i)
Answers
The equation that shows an example of the associative property of addition is:
\(\((-7+i)+7i = -7 + (i+7i)\)\)
According to the associative property of addition, the grouping of numbers being added does not affect the result. In this equation, we can see that both sides of the equation represent the addition of three terms:
\(\((-7+i)\), \(7i\),\) and \(\(i\).\) The equation shows that we can group the terms in different ways without changing the sum.
The equation \(\((-7+i)+7i = -7 + (i+7i)\)\) demonstrates the associative property by grouping \(\((-7+i)\)\) and \(\(7i\)\) together on the left side of the equation, and \(\(-7\)\) and \(\((i+7i)\)\) together on the right side of the equation. Both sides yield the same result, emphasizing the associative nature of addition.
To know more about equation visit-
brainly.com/question/9970716
#SPJ11\(\((-7+i)+7i = -7 + (i+7i)\)\)
Aaron tracks the time it takes him to mow lawns by writing coordinate points relating x, the time in hours it takes to mow a lawn, and y, the area of land mowed in acres. Two of his points are (3, 1.5) and (5, 2.5). Which statement describes the slope of the line through these two points?
Answers
Answer:
Aaron;s rate for mowing lawns is 0.5 acres per hour."as1.5 acres / 3 hours = 0.5 acres an hour2.5 acres / 5 hours = 0.5 acres an hour Option (B)
Step-by-step explanation:Aaron;s rate for mowing lawns is 0.5 acres per hour."as1.5 acres / 3 hours = 0.5 acres an hour2.5 acres / 5 hours = 0.5 acres an hour
Find the sum of the interior angles of a polygon that has 9 sides?
Answers
Answer: (9 - 2) ⋅ 180 ° = 7 ⋅ 180 ° = 126 0 °
Step-by-step explanation: