Find the error(s) and solve the problem correctly.
solve for g(f(0) if f(x) =3x-7/4 g(x)= 2x-1
answer: g(f(0) = 3(2x-1)-7/4 = 6x-1-7/4 =6x-8/4 = 6(0)-8/4 = -2
Answers
the composition of functions gives:
g(f(0)) = -6
How to solve the composition of functions?Here we have the two functions:
f(x) = 3(x - 7)/4
g(x) = 2x - 1
The problem in the answer is in the third step, where the distribution is done incorrectly.
g(f(x)) = 3*( (2x - 1) - 7)/4
g(f(x)) = 3*( 2x - 8)/4
g(f(x)) = ( 6x - 24)/4
Evaluating in x = 0 we get:
g(f(0)) = ( 6*0 - 24)/4 = -24/4 = -6
That is the solution of the composition of functions.
If you want to learn more about composition of functions:
https://brainly.com/question/10687170
#SPJ1
Answer:
The mistake is in the third step
Related Questions
On a coordinate plane, a curved line with a minimum value of (negative 2, negative 6) and maximum values of (negative 3.75, 3) and (0.25, 13), crosses the x-axis at (negative 4, 0), (negative 3, 0), (negative 1, 0), and (1, 0), and crosses the y-axis at (0, 12).
Which interval for the graphed function contains the local minimum?
[–1, 1]
[1, 2]
[–3, –1]
[–5, –3]
Answers
Answer:
Its C. (-3,-1) not B.
Step-by-step explanation:
I just took the Unit test so trust me and become my friend plssss
Answer:
yes c on edge 21' is correct
Step-by-step explanation:
a patient is admitted to the hospital because of vomiting that has lasted 3 days despite minimal intake and severe abdominal distention and pain. which intervention should the nurse perform first?
Answers
In this case, the nurse should perform a complete physical exam to determine the cause of the patient’s symptoms. The nurse should also assess the patient's vital signs, including heart rate, blood pressure, and temperature.
Once the assessment is completed, the nurse should immediately initiate fluid resuscitation to prevent dehydration and hypovolemic shock. The nurse should also administer pain medication as ordered and elevate the head of the bed to relieve abdominal distention.In this case, the patient is exhibiting symptoms of dehydration, including vomiting and minimal intake, which may result in hypovolemic shock. The patient is also experiencing severe abdominal distention and pain, which may indicate a gastrointestinal obstruction or perforation. These symptoms can be life-threatening and require immediate intervention by the nurse. Therefore, the nurse should perform a complete physical examination to determine the cause of the patient's symptoms. This examination should include a detailed abdominal assessment, such as auscultation for bowel sounds, palpation for tenderness and rigidity, and percussion for the presence of ascites. The nurse should also assess the patient's vital signs, including heart rate, blood pressure, and temperature. The nurse should also monitor the patient's urine output to ensure adequate fluid replacement and to detect any signs of renal failure. The nurse should administer pain medication as ordered and elevate the head of the bed to relieve abdominal distention.
In conclusion, the nurse should perform a complete physical exam to determine the cause of the patient’s symptoms. The nurse should also assess the patient's vital signs, including heart rate, blood pressure, and temperature. Once the assessment is completed, the nurse should immediately initiate fluid resuscitation to prevent dehydration and hypovolemic shock. The nurse should also administer pain medication as ordered and elevate the head of the bed to relieve abdominal distention.
To know more about abdominal distention visit:
brainly.com/question/31710045
#SPJ11
Can someone help me please with all these pleaseeee

Answers
/
/
/
/
/
/
:
sssss
calculate the taylor polynomials 2 and 3 centered at =0 for the function ()=16tan().
Answers
Taylor polynomials of degree 2 and 3 centered at x = 0 for the function f(x) = 16tan(x) are:
P2(x) = 16x + 8x^2
P3(x) = 16x + 8x^2
To find the Taylor polynomials centered at x = 0 for the function f(x) = 16tan(x), we can use the Taylor series expansion for the tangent function and truncate it to the desired degree.
The Taylor series expansion for tangent function is:
tan(x) = x + (1/3)x^3 + (2/15)x^5 + (17/315)x^7 + ...
Using this expansion, we can find the Taylor polynomials of degree 2 and 3 centered at x = 0:
Degree 2 Taylor polynomial:
P2(x) = f(0) + f'(0)(x - 0) + (1/2!)f''(0)(x - 0)^2
= 16tan(0) + 16sec^2(0)(x - 0) + (1/2!)16sec^2(0)(x - 0)^2
= 0 + 16x + 8x^2
Degree 3 Taylor polynomial:
P3(x) = P2(x) + (1/3!)f'''(0)(x - 0)^3
= 0 + 16x + 8x^2 + (1/3!)(48sec^2(0)tan(0))(x - 0)^3
= 16x + 8x^2
Therefore, the Taylor polynomials of degree 2 and 3 centered at x = 0 for the function f(x) = 16tan(x) are:
P2(x) = 16x + 8x^2
P3(x) = 16x + 8x^2
Learn more about taylor polynomials at https://brainly.com/question/31978863
#SPJ11
if f(1)-3 and f(n)=f(n-1) +4 then find the value of f(5)
Answers
Answer:
f(1) = 3
f(2) = -2 * 3 + 1 = -5
f(3) = -2 * -5 + 1 = 11
f(4) = -2 * 11 + 1 = -21
f(5) = -2 * -21 + 1 = 43
Step-by-step explanation:
Helppppppo meeeeeee plssssssssssssss

Answers
1)
it took
25 min : 35 mile
?? min : 70 mile
cross multiply we get 50 minutes
25 x 70 then divide by 35
2) we used:
4 cups : 90 batches
? cups. : 112.5 batches
cross multiply we get: 5 cups
112.5 x 4 then divide by 90
Solve x+2=1/2x-1 Please hurry!
Answers
Answer:
X = - 6Step-by-step explanation:
x + 2 = 1/2x - 1\(2 + 1 = \frac{1}{2}x - x\)
\(3 = - \frac{1}{2}x\)
\(x = \frac{ - 3}{ \frac{1}{2} } \\ x = \frac{ - 6}{1} \\ x = - 6\)
Hope this helps :)
Evaluate each expression.5. -36.97. 13 +-28. -12-8
Answers
7) 13 + -2 = 13 + (-2) = 13 - 2 = 11
8) -12 - 8 = - (12 + 8) = - (20) = -20
6.
The Solia family has a large garden that is 20 m by 14 m. They want to put in
a circular spa pool in a corner of the garden, as shown in the diagram.
3 m
3 m
Answers
Answer:
Am sorry but I think you forgot to add the photo of the diagram so please edit your question
question 21 options: suppose the american kennel club estimates that 38% of households in u.s. have a pembroke welsh corgi. a random sample of 400 households is taken. round probability answers to 4 decimal places, i.e. .xxxx do not include leading or ending zeros. what is the probability the sample proportion is more than 40%?
Answers
The probability that the sample proportion is more than 40% is approximately .0001.
What is Probability?
Probability is a branch of mathematics in which the chances of experiments occurring are calculated. It is by means of a probability, for example, that we can know from the chance of getting heads or tails in the launch of a coin to the chance of error in research.
To find the probability that the sample proportion is more than 40%, we need to use the normal distribution and the central limit theorem.
The central limit theorem states that the distribution of the sample mean approaches a normal distribution as the sample size increases, regardless of the shape of the population distribution.
To find the probability that the sample proportion is more than 40%, we need to first calculate the mean and standard deviation of the sample proportion. The mean of the sample proportion is equal to the population proportion (38%), and the standard deviation of the sample proportion is equal to:
\(standard\ deviation = sqrt((population\ proportion * (1 - population\ proportion)) / sample\ size)\\\\= \sqrt{((.38 * .62) / 400)}\\\\= .048\)
Next, we need to standardize the sample proportion of 40% by subtracting the mean and dividing by the standard deviation:
z = (40% - 38%) / .048 = 4.17
The probability that it is less than or equal to 40% is approximately .9999.
The probability that the sample proportion is more than 40% is then equal to 1 - .9999 = .0001.
So, The probability that the sample proportion is more than 40% is approximately .0001.
To know more about Probability visit,
https://brainly.com/question/13604758
#SPJ4
Question content area top
Part 1
A company is designing a new cylindrical water bottle. The volume of the bottle will be 155 cm3. The height of the water bottle is 8. 4 cm. What is the radius of the water bottle? Use 3. 14 for pie
Answers
The volume of the water bottle is 155 cm³ and the height is 8.4 cm. The radius of the water bottle is approximately 2.25 cm.
The formula to calculate the volume of a cylinder is V = πr²h, where V is the volume, r is the radius, h is the height, and π is pi (approximately equal to 3.14). In this case, we know that the volume of the water bottle is 155 cm³ and the height is 8.4 cm.
We can rearrange the formula to solve for the radius, r:
V = πr²h
155 = 3.14 × r² × 8.4
155 = 26.376 × r²
r² = 155 ÷ 26.376
r² ≈ 5.87
r ≈ √5.87
r ≈ 2.25
Therefore, the radius of the water bottle is approximately 2.25 cm.
Learn more about volume here
https://brainly.com/question/27710307
#SPJ11
A greengrocer buys 20 cases of oranges at a cost of $15 per case. Each case contains 10 kg of oranges. If he sells the oranges at $4/kg, how many kilograms must he sell before he makes a profit? If he sells all the oranges what will be his profit?
Answers
Answer:greengrocer should Dell 17 kg before profit. 500$ profit
Step-by-step explanation:
If the area of a circle is 36*pi square units, then the radius will be
Answers
We have a circle that has an area of 36π square units.
We have to find the radius.
The area in function of the radius is πr², so we can find the radius r as:
\(\begin{gathered} A=36\pi \\ \pi r^2=36\pi \\ r^2=\frac{36\pi}{\pi} \\ r^2=36 \\ r=\sqrt{36} \\ r=6 \end{gathered}\)Answer: the radius is 6 units.
Plot the vector field F(x,y)=(xy,x+y^2) Calculate divF.
Determine where divF>0 and where divF<0.
Answers
The divergence of the vector field F is positive for y > -1/3 and negative for y < -1/3.
To plot the vector field F(x, y) = (xy, x + y^2), we can first visualize the vectors at various points in the xy-plane. Let's choose a range of values for x and y and calculate the corresponding vectors. We'll use a step size of 1 for simplicity.
Here is a sample grid of points and their corresponding vectors:
(x, y) = (-2, -2) -> F(-2, -2) = (4, 2)
(x, y) = (-1, -2) -> F(-1, -2) = (2, 2)
(x, y) = (0, -2) -> F(0, -2) = (0, 2)
(x, y) = (1, -2) -> F(1, -2) = (0, 2)
(x, y) = (2, -2) -> F(2, -2) = (4, 2)
(x, y) = (-2, -1) -> F(-2, -1) = (2, 1)
(x, y) = (-1, -1) -> F(-1, -1) = (1, 1)
(x, y) = (0, -1) -> F(0, -1) = (0, 1)
(x, y) = (1, -1) -> F(1, -1) = (0, 1)
(x, y) = (2, -1) -> F(2, -1) = (2, 1)
... and so on for other values of y and for positive values of y.
To calculate the divergence (divF) of the vector field, we need to find the partial derivatives of the components of F with respect to x and y. Then we sum these partial derivatives.
F(x, y) = (xy, x + y^2)
∂F/∂x = y
∂F/∂y = 1 + 2y
divF = ∂F/∂x + ∂F/∂y = y + (1 + 2y) = 3y + 1
Now, we can analyze where the divergence is positive (divF > 0) and where it is negative (divF < 0).
For divF > 0:
If y > -1/3, then divF > 0.
For divF < 0:
If y < -1/3, then divF < 0.
Know more about vector field here;
https://brainly.com/question/102477
#SPJ11
true/false: the this pointer is automatically passed to static member functions of a class.
Answers
The given statement "The this pointer is not automatically passed to static member functions of a class." is false as static member functions can be called without creating an object of the class, and the "this" pointer is used to refer to the current instance of the class. Since no instance is required for static member functions, the "this" pointer is not applicable in this case.
In object-oriented programming, a class is a blueprint for creating objects, and member functions are functions defined within a class that can be called on objects of that class.
Static member functions, also known as class methods, are special member functions that are associated with the class itself rather than any specific object or instance of the class. They are declared using the "static" keyword.
Since static member functions do not operate on specific instances of the class, they do not have access to the "this" pointer. The "this" pointer is a hidden pointer that points to the current object instance, allowing non-static member functions to access the data members and other member functions of the object. However, static member functions do not have this pointer because they are not tied to any specific object.
Static member functions can only access static members of the class, which include static variables and other static member functions. They can be called using the class name itself, without creating an instance of the class. This is because they are not associated with any particular object but rather with the class as a whole.
To learn more about static member function: https://brainly.com/question/31563511
#SPJ11
random variables x and y are independent exponential random variables with e[x]=e[y]=16.find the pdf of w=x y.
Answers
The pdf of W is: fw(w) = dFw(w)/dw = (1/16) \(e^{(-w/16)}\) for w>=0 .This is the pdf of a Gamma distribution with shape parameter 2 and scale parameter 16.
Since x and y are independent exponential random variables with E[x] = E[y] = 16, we have the pdf of x and y as:
fX(x) = (1/16) \(e^{(-x/16)}\)for x>=0
fY(y) = (1/16) \(e^{(-y/16)}\)for y>=0
Let W = XY, and we need to find the pdf of W. We can find the cumulative distribution function (CDF) of W and then differentiate it to find the pdf.
The CDF of W is given by:
Fw(w) = P(W<=w) = P(XY<=w) = ∫∫[xy<=w] fX(x) fY(y) dx dy
where [xy<=w] is the indicator function, which takes the value 1 if xy<=w and 0 otherwise.
Since x and y are non-negative, we can write:
Fw(w) = ∫∫[xy<=w] (1/256) \(e^{(-x/16)}\) \(e^{(-y/16)}\) dx dy
= (1/256) ∫∫[xy<=w] \(e^{(-x/16-y/16)}\) dx dy
Let's make a change of variables and define u = x+y and v = x. Then we have:
x = v
y = u-v
The Jacobian of this transformation is 1, so we have:
Fw(w) = (1/256) ∫∫[uv<=w] \(e^{(-u/16)}\) du dv
We can split the integral as:
Fw(w) = (1/256) ∫[0,w] ∫[v,∞] \(e^{(-u/16)}\) du dv
= (1/256) ∫[0,w] 16\(e^{(-v/16)}\) dv
= 1 - \(e^{(-w/16)}\)
Therefore, the pdf of W is: fw(w) = dFw(w)/dw = (1/16) \(e^{(-w/16)}\) for w>=0
This is the pdf of a Gamma distribution with shape parameter 2 and scale parameter 16.
Learn more about “ cumulative distribution function (CDF) “ visit here;
https://brainly.com/question/31479018
#SPJ4
The last digit in 7 to the power of 5 to the power of 3
(AKA 15)

Answers
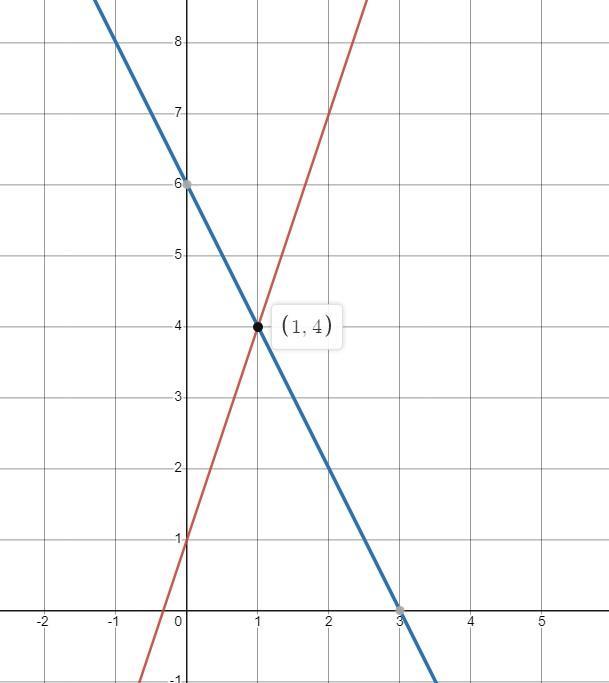
Graph the equation y=-2x+6
PLS HELP!!

Answers
first, graph the y intercept (red). This is the value of y when x is 0.
next, see if the slope is positive or negative. Positive means it goes upwards as x gets bigger, negative means it goes down. Since the slope is -2, it goes down.
Then, because it's negative 2, go down 2 and over 1 (blue). do this as many times as you like (you need only 2 points but more is a good way to double check)
Last thing is make a line that connects your points (yellow).

Answer:
The solution is (1,4)
Step-by-step explanation:
Find the Volume if the height is 10 cm and radius 3 cm? Round to the nearest
whole number
Answers
\(282.8cm pa brainlest po\)
Mike can drive his car 66km on petrol worth Rs.384. How much money does he need to reach his hometown from Delhi by car distance between his hometown from Delhi=6006km
Answers
Answer:
Rs.34,944
Step-by-step explanation:
(6006 km)/(66 km) = 91
The distance from his hometown to Delhi is 91 times 66 km.
He will need 91 times the amount of petrol.
91 * Rs.384 = Rs.34,944
Find the vector v with the given magnitude and the same direction as u.Magnitude: ||v|| = 8Direction: u = -2i
Answers
Given the following:
||v|| = 8u = -2i
We are asked to find the vector v with the given magnitude and the same direction as u. The direction of a vector is given by a unit vector. A unit vector is defined as the magnitude of the vector divided by the magnitude of the vector. Therefore, we need to find a unit vector in the same direction as u.
Using the given direction of u, we can find the magnitude of u:
|u| = √((2i)^2) = √4 = 2
Now we can find the unit vector: u/|u| = (-2i)/2 = -i
Thus, the vector v with the same direction as u is: v = (8)(-i) = -8i
Therefore, the answer is:
Vector v with the given magnitude and the same direction as u is v = -8i
Finding vector v with given magnitude and same direction as u : https://brainly.com/question/31053420
#SPJ11
Consider the function f(x,y)=2x2−4x+y2−2xy subject to the constraints x+y≥1xy≤3x,y≥0 (a) Write down the Kuhn-Tucker conditions for the minimal value of f. (b) Show that the minimal point does not have x=0.
Answers
The minimal point does not have x = 0.
(a) Kuhn-Tucker conditions for the minimal value of fThe Kuhn-Tucker conditions are a set of necessary conditions for a point x* to be a minimum of a constrained optimization problem subject to inequality constraints. These conditions provide a way to find the optimal values of x1, x2, ..., xn that maximize or minimize a function f subject to a set of constraints. Let's first write down the Lagrangian: L(x, y, λ1, λ2, λ3) = f(x, y) - λ1(x+y-1) - λ2(xy-3) - λ3x - λ4y Where λ1, λ2, λ3, and λ4 are the Kuhn-Tucker multipliers associated with the constraints. Taking partial derivatives of L with respect to x, y, λ1, λ2, λ3, and λ4 and setting them equal to 0, we get the following set of equations: 4x - 2y - λ1 - λ2y - λ3 = 0 2y - 2x - λ1 - λ2x - λ4 = 0 x + y - 1 ≤ 0 xy - 3 ≤ 0 λ1 ≥ 0 λ2 ≥ 0 λ3 ≥ 0 λ4 ≥ 0 λ1(x + y - 1) = 0 λ2(xy - 3) = 0 From the complementary slackness condition, λ1(x + y - 1) = 0 and λ2(xy - 3) = 0. This implies that either λ1 = 0 or x + y - 1 = 0, and either λ2 = 0 or xy - 3 = 0. If λ1 > 0 and λ2 > 0, then x + y - 1 = 0 and xy - 3 = 0. If λ1 > 0 and λ2 = 0, then x + y - 1 = 0. If λ1 = 0 and λ2 > 0, then xy - 3 = 0. We now consider each case separately. Case 1: λ1 > 0 and λ2 > 0From λ1(x + y - 1) = 0 and λ2(xy - 3) = 0, we have the following possibilities: x + y - 1 = 0, xy - 3 ≤ 0 (i.e., xy = 3), λ1 > 0, λ2 > 0 x + y - 1 ≤ 0, xy - 3 = 0 (i.e., x = 3/y), λ1 > 0, λ2 > 0 x + y - 1 = 0, xy - 3 = 0 (i.e., x = y = √3), λ1 > 0, λ2 > 0 We can exclude the second case because it violates the constraint x, y ≥ 0. The first and third cases satisfy all the Kuhn-Tucker conditions, and we can check that they correspond to local minima of f subject to the constraints. For the first case, we have x = y = √3/2 and f(x, y) = -1/2. For the third case, we have x = y = √3 and f(x, y) = -2. Case 2: λ1 > 0 and λ2 = 0From λ1(x + y - 1) = 0, we have x + y - 1 = 0 (because λ1 > 0). From the first Kuhn-Tucker condition, we have 4x - 2y - λ1 = λ1y. Since λ1 > 0, we can solve for y to get y = (4x - λ1)/(2 + λ1). Substituting this into the constraint x + y - 1 = 0, we get x + (4x - λ1)/(2 + λ1) - 1 = 0. Solving for x, we get x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4. We can check that this satisfies all the Kuhn-Tucker conditions for λ1 > 0, and we can also check that it corresponds to a local minimum of f subject to the constraints. For this value of x, we have y = (4x - λ1)/(2 + λ1), and we can compute f(x, y) = -3/4 + (5λ1^2 + 4λ1 + 1)/(2(2 + λ1)^2). Case 3: λ1 = 0 and λ2 > 0From λ2(xy - 3) = 0, we have xy - 3 = 0 (because λ2 > 0). Substituting this into the constraint x + y - 1 ≥ 0, we get x + (3/x) - 1 ≥ 0. This implies that x^2 + (3 - x) - x ≥ 0, or equivalently, x^2 - x + 3 ≥ 0. The discriminant of this quadratic is negative, so it has no real roots. Therefore, there are no feasible solutions in this case. Case 4: λ1 = 0 and λ2 = 0From λ1(x + y - 1) = 0 and λ2(xy - 3) = 0, we have x + y - 1 ≤ 0 and xy - 3 ≤ 0. This implies that x, y > 0, and we can use the first and second Kuhn-Tucker conditions to get 4x - 2y = 0 2y - 2x = 0 x + y - 1 = 0 xy - 3 = 0 Solving these equations, we get x = y = √3 and f(x, y) = -2. (b) Show that the minimal point does not have x=0.To show that the minimal point does not have x=0, we need to find the optimal value of x that minimizes f subject to the constraints and show that x > 0. From the Kuhn-Tucker conditions, we know that the optimal value of x satisfies one of the following conditions: x = y = √3/2 (λ1 > 0, λ2 > 0) x = √3 (λ1 > 0, λ2 > 0) x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4 (λ1 > 0, λ2 = 0) If x = y = √3/2, then x > 0. If x = √3, then x > 0. If x = (1 + λ1 + √(λ1^2 + 10λ1 + 1))/4, then x > 0 because λ1 ≥ 0.
To know more about constraints, visit:
https://brainly.com/question/17156848
#SPJ11
solve the following system of equations using the substitution method. –6x 2y = 8 y = 3x 4 question 9 options: a) no solution b) (0, 4) c) infinitely many solutions d) (8, 8)
Answers
The correct answer is option c) infinitely many solutions..
To solve the system of equations using the substitution method, we'll substitute the value of y from the second equation into the first equation and solve for x.
Given:
-6x + 2y = 8 ---(1)
y = 3x + 4 ---(2)
Substitute equation (2) into equation (1):
-6x + 2(3x + 4) = 8
Simplify:
-6x + 6x + 8 = 8
8 = 8
We obtained a true statement (8 = 8), which means the two equations are equivalent. This solution shows that the system has infinitely many solutions.
Therefore, the correct answer is option c) infinitely many solutions..
know more about substitution method
https://brainly.com/question/22340165
#SPJ11
What is the least integer? explain.
Answers
Answer:
The function whose value at any number x is the smallest integer greater than of equal to x is called the least integer function.
Step-by-step explanation:
It is denoted by ⌈x⌉ It is also known as ceiling of x. For example ⌈3.578⌉ = 4 , ⌈0.78⌉ = 1 , ⌈-4.64⌉ = - 4.
A shop advertises 10% off its prices in a sale.
A book is £6.30 in the sale
How much was it before the price reduction?
Answers
Answer:
£7
Step-by-step explanation:
Since the sale is 10% the original price, every item is being sold for 90% of its original price. Now the problem is: £6.30 is 90% of what number?
Let x = original price before sale
6.30 = 0.9x
0.9x = 6.3
Divide both sides by 0.9
x = 6.3/0.9
x = 7
Answer: £7
The Presidential election was quite tight, with Obama winning with 51 % of the votes. There were 126 million voters in the 2012 US Presidential election. What percentage of the final voters was targeted with unique profiles with this big data project
Answers
The percentage would be 7.94%.
In the 2012 US Presidential election, there were 126 million voters, and Barack Obama won with 51% of the votes. To determine the percentage of the final voters targeted with unique profiles through the big data project, we need more information about the project's objectives and scope.
The given information about the election outcome (Obama winning with 51% of the votes) is not directly related to the big data project's details. The big data project might have involved collecting and analyzing data from various sources to understand voter behavior, demographics, preferences, or other factors that could influence the election outcome. It could have targeted specific groups of voters with tailored messages, ads, or outreach campaigns based on the insights gained from the data analysis.
Without additional information about the big data project, such as the specific voter segments targeted or the goals of the project, we cannot calculate the percentage of final voters targeted with unique profiles. The percentage would depend on the project's goals and how many voters fell into the targeted segments. For example, if the project targeted 10 million voters out of the 126 million, the percentage would be 10 million / 126 million = 7.94%.
To determine the percentage accurately, we would need a comprehensive understanding of the big data project's methodology, data sources, and the specific criteria used to target voters with unique profiles. Only with this detailed information could we calculate the percentage of voters targeted by the big data project.
Learn more about percentage here:
brainly.com/question/32197511
#SPJ11
Draw a flow diagram to indicate the different phases in reproduction.
Answers
Answer:
ovulation fertilization cell division implantation conception delivery
Find the perimeter in simplest from

Answers
Answer: 4x(cubed) + 6x(squared)+11x+3
Step-by-step explanation:
3/5 (-20 Divied by 1/3 ) (-2/3)
Answers
The fraction 3/5 (-20 Divied by 1/3 ) (-2/3) is simplified is -6
What is a fraction?A fraction can simply be defined as the part of a whole number or element.
The different types of fractions are;
Simple fractionsProper fractionsImproper fractionsComplex fractionsFrom the information given, we have the fractions;
3/5 (-20/ 1/3 ) (-2/3)
expand the bracket
3/ 5 × 20 × 3/1 × -2/3
Divide the common factors
3/ 1 × 4 × 3/1 × -2/3
Multiply the values
-72/12
Divide the values
-6
Hence, the value is -6
Learn more about fractions here:
https://brainly.com/question/11562149
#SP1
find the equation of the line tangent to f(x)=−2sin(x) at x=34π.
Answers
the equation of the line tangent to f(x) = -2sin(x) at x = 34π is y = -2x + 68π + 2sin(34π).
To find the equation of the line tangent to the function f(x) = -2sin(x) at x = 34π, we need to find the slope of the tangent line at that point, and then use the point-slope form of the equation of a line.
The slope of the tangent line is equal to the derivative of the function at x = 34π. We can find the derivative of f(x) using the chain rule:
f'(x) = -2cos(x)
Therefore, f'(34π) = -2cos(34π) = -2.
This means that the slope of the tangent line is -2 at x = 34π.
To find the equation of the tangent line, we also need a point on the line. Since the tangent line passes through the point (34π, f(34π)), we can use this point as the point-slope form of the equation of the line:
y - f(34π) = m(x - 34π)
Substituting the values we have found, we get:
y - (-2sin(34π)) = -2(x - 34π)
Simplifying, we get:
y = -2x + 68π + 2sin(34π)
To know more about equation visit:
brainly.com/question/10413253
#SPJ11