Find the distance from the point P
(5, 3) to the line x = 7
Answers
Answer:
\(d = \sqrt{13} \: units\)
Step-by-step explanation:
distance from the point P
(5, 3) to the line x = 7 = (7, 0)
\(d = \sqrt{ {(7 - 5)}^{2} + {(0 - 3)}^{2} } \\ \\ d = \sqrt{ {(2)}^{2} + {( - 3)}^{2} } \\ \\ d = \sqrt{4 + 9} \\ \\ d = \sqrt{13} \: units\)
Related Questions
Help me i really need help please

Answers
Answer:
16.4%
Step-by-step explanation:
$1665=100%
$53.40=?
53.40×100÷1665
=16.4%
Solve the initial-value problem of the 2nd order homogeneous differential equation I y" + 16 y = 0, y(0) = y'(0) = -2.
Answers
The particular solution of the given differential equation is : y(x) = -2cos(4x) - (1/2)sin(4x).
Given the differential equation is: I y" + 16 y =0 with initial values y(0) = -2, and y'(0) = -2.
We have to find the solution of the differential equation. We know that the standard form of a second-order homogeneous differential equation is:
y"+p(x)y'+q(x)y=0
The characteristic equation is obtained by substituting y=e^(mx) in the above equation. The characteristic equation is:
m²+p(x)m+q(x)=0
Comparing the above equation with
y" + 16 y = 0, we have,
p(x) = 0 and q(x) = 16
Therefore, the characteristic equation becomes:
m² + 16 = 0
m = ±4i
Hence, the general solution of the given differential equation is:
y(x) = c1cos(4x) + c2sin(4x). Now, let us apply the initial conditions:
y(0) = c1 = -2
Also, y'(x) = -4c1sin(4x) + 4c2cos(4x)Therefore,
y'(0) = 4= c2 = -2
c2 = -1/2
Therefore, the particular solution of the given differential equation is y(x) = -2cos(4x) - (1/2)sin(4x).
To know more about the differential equation, visit:
brainly.com/question/32524608
#SPJ11
HELP ASAP PLSSSSS
(picture of graph is below)
Below are the data collected from two random samples of 500 American adults on the number of hours they spend doing leisure and sports activities per day (rounded to the nearest hour):
Number of hours spent doing leisure and sports activities per day 1 2 3 4 5
Sample A: Number of adults 70 90 135 140 65
Sample B: Number of adults 80 80 130 135 75
Dan concludes that adults spend a mean of 3 hours each day doing leisure and sports activities. Bret thinks the mean is 4 hours. Who is correct—Dan or Bret? Explain your answer in two or three sentences. Make sure to use facts to support your answer.

Answers
Answer:
Dan is correct
Step-by-step explanation:
Mean = the sum of all data values divided by the total number of data values
Number of adults in Sample A:
= 70 + 90 + 135 + 140 + 65 = 500
Mean of Sample A:
= [ (1 × 70) + (2 × 90) + (3 × 135) + (4 × 140) + (5 × 65) ] ÷ 500
= 1540 ÷ 500
= 3.08
Number of adults in Sample B:
= 80 + 80 + 130 + 135 + 75 = 500
Mean of Sample A:
= [ (1 × 80) + (2 × 80) + (3 × 130) + (4 × 135) + (5 × 75) ] ÷ 500
= 1545 ÷ 500
= 3.09
Mean of the two samples:
= (3.08 + 3.09) ÷ 2
= 3.085 hours
= 3 hours (nearest hour)
The mean of Sample A is 3.08 hours and the mean of Sample B is 3.09 hours, so the mean of the entire sample is 3.085 hours. If we round this to the nearest hour, then the mean is 3 hours. Therefore, Dan is correct in concluding that the adults spend a mean of 3 hours each day doing leisure and sports activities.
Jen can write 200 words in 6 minutes.
What expression represents the unit rate, in words per minute?
A ) 6/200
B ) 6/1
C ) 200/6
D ) 200/1
Answers
Answer:
im pretty sure its c 200/6
Step-by-step explanation:
What is the value of y?
65°
36°

Answers
Answer:
y = 79
Step-by-step explanation:
65 + 36 + y = 180
101 + y = 180
y = 79
What’s 5x + 5 factored?
Answers
Answer:
5(x+1)
Step-by-step explanation:
So factor is to make it simplified like x(y+c) {I made up random variable for an example but almost all factored problems look like this}
So first find the Greatest Common Factor or GCF for short
The GCF between 5x and 5 is 5
So you divide the whole thing by 5
5x+5/5
you’d get x+1
Now for the 5 just put it around X+1 but with parenthesis
5(x+1)
Write an equation of the line in point-slope form passing through the point and parallel to the given line.3-X + 52(1,-1) y = 2
Answers
Answer:
Explanation:
The slope of the given line is 3/2
A line parallel to this has the same line but different y-intercept.
IIn point-slope form, it is:
\(y-y_1=m(x-x_1)_{}\)Where
\(\begin{gathered} x_1=1 \\ y_1=-1 \\ m=\frac{3}{2} \end{gathered}\)Using these, we have:
\(\begin{gathered} y-(-1)=\frac{3}{2}(x-1) \\ \\ y+1=\frac{3}{2}(x-1) \end{gathered}\)a) estimate the area under the graph of f(x)=7x from x=1 to x=5 using 4 approximating rectangles and right endpoints. estimate = (b) repeat part (a) using left endpoints. estimate =
Answers
The estimate for the area under the graph of f(x) = 7x from x = 1 to x = 5 using 4 approximating rectangles and right endpoints is 84. The estimate using left endpoints is 70.
To estimate the area under the graph using rectangles, we divide the interval [1, 5] into smaller subintervals. In this case, we have 4 rectangles, each with a width of 1. The right endpoint of each subinterval is used as the height of the rectangle. We can also use the right Riemann sum approach.
For the first rectangle, the height is f(2) = 7(2) = 14. For the second rectangle, the height is f(3) = 7(3) = 21. For the third rectangle, the height is f(4) = 7(4) = 28.And for the fourth rectangle, the height is f(5) = 7(5) = 35.Adding up the areas of the rectangles, we get 14 + 21 + 28 + 35 = 98.
However, since the rectangles extend beyond the actual area, we need to subtract the excess.
The excess is equal to the area of the rightmost rectangle that extends beyond the graph, which has a width of 1 and a height of f(6) = 7(6) = 42.
Subtracting this excess, we get an estimate of 98 - 42 = 56.
Dividing this estimate by 4, we obtain 14, which is the area of each rectangle.
Hence, the estimate for the area under the graph using right endpoints is 4 * 14 = 56.
Similarly, we can calculate the estimate using left endpoints by using the left endpoint of each subinterval as the height of the rectangle.
In this case, the estimate is 4 * 14 = 56.
Therefore, the estimate using left endpoints is 56.
To learn more about Riemann sum visit:
brainly.com/question/30766300
#SPJ11
Drag the labels to the correct locations on the image. Not all lables will be used. Consider function h. What is the range of function h?
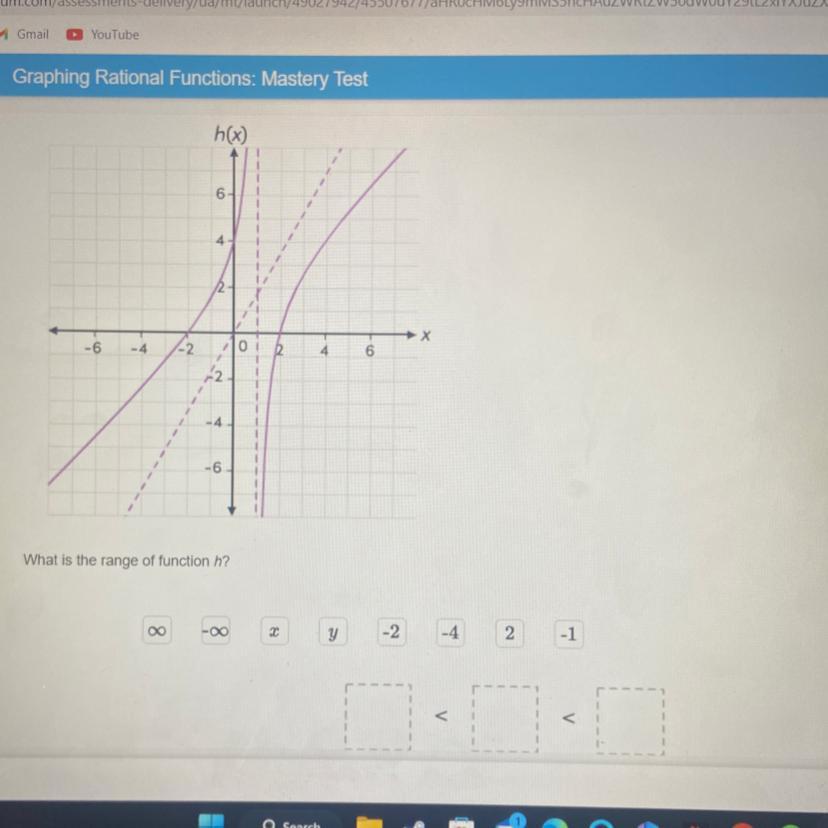
Answers
The range of the graphed function is expressed as: -∞ < y < ∞
How to find the range of the graph Function?Range corresponds to the values on the y-axis while the Domain corresponds to values on the x-axis.
From the graph of a function h(x), we want to find the range of the function in inequality notation.
The range is all possible y-values of the function. Thus, let's find all possible y-values from the graph.
If we look at the graph closely, we see that it has a vertical asymptote at x = 1 and a slant asymptote.
But it includes all y values from -infinity to infinity.
Thus, we can write range as -∞< y < ∞ because both sides of the function go and so on below the x-axis and go and so on above the x-axis.
The range is -∞< y < ∞ .
Read more about Range of Graph Function at: https://brainly.com/question/7954282
#SPJ1
Simplifying algebraic expression
-8w-b/9 use b=36 & w=2
The b/9 is b over 9
Answers
Answer:
-20
Step-by-step explanation:
-8*2-36/9
-16-4
-20
express as a single simplified fraction. 3m^2-3n^2/m^2+mp divided by 6m-6n/p+m
Answers
The single simplified fraction is (m + n)(p + m) / 2m.
To simplify the expression
\((3m^2 - 3n^2) / (m^2 + mp)÷ (6m - 6n) / (p + m)\)
we need to invert the second fraction and multiply by the first.
\((3m^2 - 3n^2) / (m^2 + mp) \times (p + m) / (6m - 6n)\)
We can then factor out a 3 from the numerator and the denominator, and cancel out the (m - n) terms. 3(m + n)(m - n) / 3m(m - n) x (p + m) / 6(m - n)
Simplifying further, we can cancel out the 3's and the (m - n) terms. (m + n) / m x (p + m) / 2
The simplified expression is (m + n)(p + m) / 2m.
To simplify the given expression, we invert the second fraction and multiply it by the first. Then we factor out common terms and cancel out like terms. We simplify the expression to obtain the single fraction (m + n)(p + m) / 2m.
Learn more about fraction here:
https://brainly.com/question/10354322
#SPJ1
Automata and formal languages
short statements
Which of the following statements about automata and formal languages are true? Briefly justify your answers. For false statements, it is sufficient to give a counterexample. Answers without any subst
Answers
The statements that are true about automata and formal languages are b, c and d
The term empty does not exist in any language. There are dialects that do not use the empty word in their lexicon. The empty word, for instance, would not exist in a language where all words have lengths higher than zero. There exist Irregular finite languages. A language with all possible combinations of a limited number of symbols is one example.
While this language is finite, a conventional grammar cannot adequately define it. Additionally, contextless languages are a subset of regular languages. Because of this, there are irregular context-free languages. A regular grammar can be used to describe L1 if L1 is a subset of L2 and L2 is regular.
Read more about automata on:
https://brainly.com/question/33003625
#SPJ4
Complete Question:
Which of the following statements about automata and formal languages are true? Briefly justify your answers. Answers without any substantiation will not achieve points!
(a) Every language contains the empty word.
(b) There exist finite languages which are not regular.
(c) Not every context free language is regular.
(d) For two arbitrary languages L1 and L2 the following always holds: If L1 <L2, L2 is regular than L1 is also regular.
(e) Let L = (ba) be a language which contains only one word. There exists only one (unique) regular expression which generates L, and this expression is a = ba.
Consider the differential equation dydt=y−tdydt=y−t.
Determine whether the following functions are solutions to the given differential equation.
1) y(t)=t+1+2ety(t)=t+1+2et.
2) y(t)=t+1y(t)=t+1.
3) y(t)=t+2y(t)=t+2.
Answers
Based on the analysis of the given functions and the given differential equation, the following conclusions can be drawn:
The function y(t) = t + 1 + 2e^t is a solution to the differential equation dy/dt = y - t.
The function y(t) = t + 1 is also a solution to the differential equation dy/dt = y - t.
The function y(t) = t + 2 is not a solution to the differential equation dy/dt = y - t.
Step-by-Step Explanation:
To determine if a given function is a solution to a differential equation, we need to perform the following steps:
Find the derivative of the given function with respect to t. This gives us the value of dy/dt.
Substitute the given function and the value of dy/dt into the differential equation and simplify the expression.
Check if the simplified expression is equal to the value of dy/dt. If they are equal, then the given function is a solution to the differential equation.
Applying this process to the three given functions, we obtain the following:
For y(t) = t + 1 + 2e^t:
Step 1: Find the derivative of y(t) with respect to t:
dy/dt = 1 + 2e^t
Step 2: Plug the function y(t) into the given equation and compare it to the found dy/dt:
y - t = (t + 1 + 2e^t) - t = 1 + 2e^t
Since dy/dt = y - t, y(t) = t + 1 + 2e^t is a solution to the differential equation.
For y(t) = t + 1:
Step 1: Find the derivative of y(t) with respect to t:
dy/dt = 1
Step 2: Plug the function y(t) into the given equation and compare it to the found dy/dt:
y - t = (t + 1) - t = 1
Since dy/dt = y - t, y(t) = t + 1 is also a solution to the differential equation.
For y(t) = t + 2:
Step 1: Find the derivative of y(t) with respect to t:
dy/dt = 1
Step 2: Plug the function y(t) into the given equation and compare it to the found dy/dt:
y - t = (t + 2) - t = 2
In this case, dy/dt ≠ y - t, so y(t) = t + 2 is not a solution to the differential equation.
Therefore, we can conclude that the first two functions are solutions to the given differential equation, while the third function is not.
Learn more about the differential equation:
https://brainly.com/question/8328980
#SPJ11
4X=80 question in assignment
Answers
Help aspp please thank you

Answers
The equation of the line would be y = (-3/4)x + 5.
What is the slope-point form of the line?
For the line having slope "m" and the point (x1, y1) the equation of the line passing through the point (x1, y1) having slope 'm' would be
y - y1 = m(x - x1)
The given equation is \(y=-\frac{3}{4}x-17\)
The required line is parallel to the given line.
and we know that the slopes of the parallel lines are equal so the slope of the required line would be m = -3/4
And the required line passes through (8, -1)
so by using slope - point form of the line,
y - (-1) = (-3/4)(x - 8)
y + 1 = (-3/4)x - (-3/4)8
y + 1 = (-3/4)x + 24/4
y = (-3/4)x + (12/2 - 1)
y = (-3/4)x + 5
Hence, the equation of the line would be y = (-3/4)x + 5.
To learn more about slope - point form of the line, visit:
https://brainly.com/question/24907633
#SPJ1
a. A Ferris wheel has a radius of 38 feet and completes one revolution (or full rotation) every 8 minutes. At what constant angular speed does the Ferris wheel rotate at (in radians per minute)? radians per minute Preview b. A Ferris wheel hast radius of 32 feet and travels
Answers
The Ferris wheel spins steadily at an angle of 4 radians per minute. 2v/80.24 radians per minute is the constant angular speed at which the Ferris wheel turns.
Using the formula: one can determine the Ferris wheel's diameter.
C = 2πr
where r denotes the Ferris wheel's diameter. If we substitute r = 38 feet, we obtain:
C = 2π(38) ≈ 238.76 feet
The Ferris wheel completes one rotation every eight minutes, so the calculation for angular speed is:
ω = θ/t
where t is the time it takes for one rotation to be completed and is the angle in radians at which the Ferris wheel rotates. The angle is equivalent to two radians, or one full rotation, so we have:
Radians per minute Equals 2/8 = 4
As a result, the Ferris wheel spins at a steady rate of /4 radians per minute.
b. The Ferris wheel's circumference can be calculated using the same method as C = 2πr
C = 2π(32) ≈ 201.06 feet
t = sqrt(2πr^2)/v = sqrt(2π(32)^2)/v ≈ 80.24/v
ω = θ/t = 2π/(80.24/v) = 2πv/80.24 radians per minute.
Because of this, the Ferris wheel spins at a constant rate of 2 v/80.24 radians per minute.
Learn more about speed here:
https://brainly.com/question/28224010
#SPJ4
please help this is due and i only got the second part done

Answers
Answer:2n+13=75 n=31
Can someone help me please?

Answers
B is the answer
Complete the table of values. Please help!

Answers
Answer:
Step-by-step explanation:
Where we have "x" must replace for the number shown on table
We have for "x" tha numbers: 0; 1; 2; 3; 4 and 5
Equation:
1.y = x+4
y = x + 4
For x = 0
y = x + 4
y = 0 + 4
y = 4
For x = 1
y = x + 4
y = 1 + 4
y = 5
For x = 2
y = x + 4
y = 2 + 4
y = 6
For x = 3
y = x + 4
y = 3 + 4
y = 7
For x = 4
y = x + 4
y = 4 + 4
y = 8
For x = 5
y = x + 4
y = 5 + 4
y = 9
So:
x y
0 4
1 5
2 6
3 7
4 8
5 9
I hope help you.
PLS HELP ME ANSWER THIS QUESTION I DONT UNDERSTAND IT I WILL GIVE BRAINLIST AND A THANK YOU!!!!

Answers
Answer:
x=150°
Step-by-step explanation:
Using the vertical angle theorem, you can infer that AEC and DEB are in fact the same angle, 20°, and the same goes for FED and CEG, both 130°.
So, x spans AEC and CEG so is 20° + 130° = 150°
A sign says that the price marked on all music equipment is 40% off the original price. You buy a drum set for the sale price of $870.What percent of the original price is the sale price?
Answers
Answer:
870 X 40% = $338.00
The original price was $1208.00
The price was marked with the discount already
40%
Step-by-step explanation:
There is a line through the origin that divides the region bounded by the parabola y=5x−3x^2 and the x-axis into two regions with equal area. What is the slope of that line?
Answers
The slope of the line that divides the region bounded by the parabola \(y=5x-3x^2\)and the x-axis into two regions with equal area is 5.
To find the slope of the line that divides the region into two equal areas, we need to determine the point of intersection between the parabola and the x-axis. Since the line passes through the origin, its equation will be y = mx, where m represents the slope.
Setting the equation of the parabola equal to zero, we find the x-values where the parabola intersects the x-axis. By solving the equation\(5x - 3x^2 = 0\), we get x = 0 and x = 5/3.
To divide the region into two equal areas, the line must pass through the midpoint between these x-values, which is x = 5/6. Plugging this value into the equation of the line, we have y = (5/6)m.
Since the areas on both sides of the line need to be equal, we can set up an equation using definite integrals. By integrating the equation of the parabola from 0 to 5/6 and setting it equal to the integral of the line from 0 to 5/6, we can solve for m. After performing the integration, we find that m = 5.
Therefore, the slope of the line that divides the region into two equal areas is 5.
Learn more about: Parabola
brainly.com/question/11911877
#SPJ11
la quema de gasolina en un automóvil libera aproximadamente 3x104 kcal/gal. si un automóvil promedia 38 km/gal cuando se conduce a 95 km/h, lo que req
Answers
The approximate energy requirement for the car when driven at 95 km/h is 789.47 kcal/km.
We have,
If a car averages 38 km/gal when driven at 95 km/h, we can calculate the fuel consumption in gallons per kilometer (gal/km).
Fuel consumption (gal/km) = 1 / (average fuel efficiency in km/gal)
Fuel consumption (gal/km) = 1 / 38
Now, to determine the energy requirement in kcal per kilometer (kcal/km), we multiply the fuel consumption by the energy released per gallon of gasoline:
Energy requirement (kcal/km) = Fuel consumption (gal/km) * Energy released per gallon (kcal/gal)
Energy requirement (kcal/km) = (1 / 38) * (3 x 10^4 kcal/gal)
Now,
Fuel consumption (gal/km) = 1 / 38
Energy requirement (kcal/km) = (1 / 38) * (3 x 10^4 kcal/gal)
Energy requirement (kcal/km) = (1 / 38) * (3 x 10^4 kcal/gal)
≈ 789.47 kcal/km
Therefore,
The approximate energy requirement for the car when driven at 95 km/h is 789.47 kcal/km.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ12
The complete question:
"Burning gasoline in a car releases approximately 3 x 10^4 kcal/gal. If a car averages 38 km/gal when driven at 95 km/h, what is the energy requirement in kcal per kilometer (kcal/km) for the car?"
which two rational numbers does the square root of 14 lies between?
Answers
The value of √14 lies between 3.70 and 3.75.
What is Radical?The √ symbol that is used to denote square root or nth roots. Radical Expression - A radical expression is an expression containing a square root.
Given:
We have to √14.
So, the value of √14 ≈ 3.74
Now, we can solve for all the answer .
A) 19/6 = 3.1666...
22/7 = 3.1428...
So, It cannot be the answer.
B) Doesn't need to be solved.
3.17
3.71
So, It cannot be the answer.
C)√4 = 2
√9 = 3
So, It cannot be the answer.
D) Doesn't need to be solved.
3.70
3.75
So, It can be the answer.
Hence, √14 lies between 3.70 and 3.75
Learn more about Radical here:
https://brainly.com/question/13941375
#SPJ1
Find the value of x.
Round to the nearest tenth.
x = [?]°
37
20
23
Law of Cosines: c² = a² + b² - 2ab cos C
![Find the value of x.Round to the nearest tenth.x = [?]372023Law of Cosines: c = a + b - 2ab cos C](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/KTLPNYxaFtg8tYgmZ7XNzBRwxVkvkRhK.png)
Answers
Answer:118.6
Step-by-step explanation:
Answer:
118.6°
Step-by-step explanation:
You want the value of the obtuse angle marked x in the triangle with sides 20, 23, and 37.
Law of CosinesIn the given triangle, the relevant formulation of the law of cosines is ...
b² = a² +c² -2ac·cos(B)
Solving for angle B, we get ...
B = arccos((a² +c² -b²)/(2ac))
B = arccos((20² +23² -37²)/(2·20·23)) ≈ 118.6°
The value of x is about 118.6°.
![Find the value of x.Round to the nearest tenth.x = [?]372023Law of Cosines: c = a + b - 2ab cos C](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/tK75tz7NmiB3shSK52OrN05rePj18EAF.png)
![Find the value of x.Round to the nearest tenth.x = [?]372023Law of Cosines: c = a + b - 2ab cos C](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/wa7TjdKrk5WJTeHQHYojPWFxpHj76v66.png)
f 75 grams of ice cream contains 10 grams of fat how many grams of fat would be in 150 grams of ice cream? Answer:
Answers
If 75 grams of ice cream contains 10 grams of fat, then 150 grams of ice cream would contain 20 grams of fat. The amount of fat is directly proportional to the weight of the ice cream.
We can set up a proportion to solve the problem. Let x represent the unknown amount of fat in 150 grams of ice cream. According to the given information, we have the proportion:
10 grams of fat / 75 grams of ice cream = x grams of fat / 150 grams of ice cream
To solve for x, we can cross-multiply and then divide:
10 * 150 = 75 * x
1500 = 75x
X = 1500 / 75 = 20
Therefore, 150 grams of ice cream would contain 20 grams of fat. This is because the ratio of fat to ice cream remains constant, so we can use this proportion to find the missing value.
Learn more about Ratio here: brainly.com/question/13419413
#SPJ11
A school's fall fundraiser raised money for new laptops and tablets for the school. The totals for the 7th-grade homerooms are shown in the table below. The mean of the data is $685.42 and the median is $635.00. Which measure, the mean or the median, is a better measure of the central tendency of the data, and why?
Answers
Answer:
It is The median, because there is an outlier that is significantly higher than the rest of the data, and it raises the mean above the center of the data, making the mean a poor choice, and the median a better choice
Step-by-step explanation:
1575 is the outlier causing the median to be the best
A party rental company has chairs and tables for rent. The total cost to rent 5 chairs and 2 tables is $22. The total cost to rent 3 chairs and 8 tables is $71. What is the cost to rent each chair and each table?
Answers
Answer:
The cost to rent each chair is $1.25 and the cost to rent each table is $8.50
Step by step:
A party rental company has chairs and tables for rent. The total cost to rent
A party rental company has chairs and tables for rent. The total cost to rent 4
chairs and 8
tables is $73
. The total cost to rent 2
chairs and 3
tables is $28
. What is the cost to rent each chair and each table?
Follow3
Add comment
More
1 Expert Answer
By:
Best
Edward C. answered • 02/10/15
TUTOR 5.0 (377)
Caltech Grad for math tutoring: Algebra through Calculus
ABOUT THIS TUTOR ›
Let C = cost to rent each chair
Let T = cost to rent each table
4C + 8T = 73
2C + 3T = 28
Multiply the 2nd equation by (-2) and then add the equations together
4C + 8T = 73
-4C - 6T = -56
2T = 17
T = 17/2 = 8.5
Plug this in to the 1st equation to solve for C
4C + 8(17/2) = 73
4C + 68 = 73
4C = 5
C = 5/4 = 1.25
So the cost to rent each chair is $1.25 and the cost to rent each table is $8.50
The cost to rent each chair and each table are $1 and $8.5 respectively.
Suppose the price of one chair =x
The price of one table =y
What is a linear equation?Any equation of the form ax+by+c=0 is called a linear equation where a, b, c∈ R.
According to the question, the total cost to rent 5 chairs and 2 tables is $22.
5x+2y=22
Multiplying it by 4 on both sides
20x+8y=88.......(1)
The total cost to rent 3 chairs and 8 tables is $71.
3x+8y=71.........(2)
Subtracting (2) from (1)
17x=17
x=1
So, y=8.5
So, the price of 1 chair =$1
the price of 1 table =$8.5
Hence, the cost to rent each chair and each table are $1 and $8.5 respectively.
To get more about linear equations visit:
https://brainly.com/question/14323743
How do you divide fractions with a whole number for dummies?
Answers
Even though dividing a fraction by a whole number might be challenging, it is simple to achieve with a few steps. By placing the full number above 1, you must first divide it into a fraction. After that, multiply the fraction you are dividing by the inverted version of the fraction. Lastly, simplify the response as much as possible.
For instance, to multiply 3/4 by 2:
Put 2 over 1, making it 2/1, to make it a fraction.
To get 1/2, invert 2/1.
To get 3/8, multiply 3/4 by 1/2.
Divide the numerator and denominator by 3 to get 1/4, which is the simplest representation of the fraction 3/8.
Hence, 1/4 is equivalent to 3/4 when divided by 2.
Learn more about fractions at
https://brainly.com/question/10354322
#SPJ4
Proportional Relationships
Solve for X

Answers
Answer:
x=9/6
Step-by-step explanation:
\( \frac{20}{16 } = \frac{12}{x} \)
12×16=192
192÷20=9.6