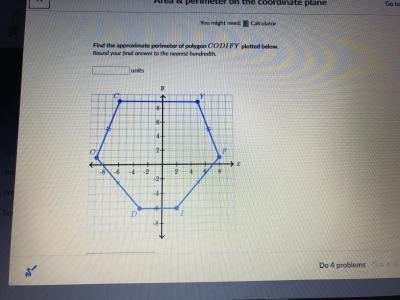
Find the approximate perimeter of polygon CODIFYCODIFYC, O, D, I, F, Y plotted below.

Round your final answer to the nearest hundredth.

please helppp

Answer:

C and E

Step-by-step explanation:

Answer:

a triangle is a closed polygon that consists of three sides and three angles,and it's one of the basic shape that we basic shape that we knowing geometry.

The magnitude of the vector difference is approximately 20.88, and the angles α and β can be calculated using the law of sines.

The magnitude of the vector difference |ã - b| can be found using the law of cosines. According to the law of cosines, the magnitude of the vector difference is given by:

|ã - b| = √(|ã|² + |b|² - 2|ã||b|cos(θ))

Substituting the given magnitudes and angle, we have:

|ã - b| = √(10² + 14² - 2(10)(14)cos(120°))

Simplifying this expression gives:

|ã - b| = √(100 + 196 - 280(-0.5))

|ã - b| = √(100 + 196 + 140)

|ã - b| = √(436)

|ã - b| ≈ 20.88

The magnitude of the vector difference |ã - b| is approximately 20.88.

To find the angles between the vector difference and each vector, we can use the law of sines. Let's denote the angle between |ã - b| and |ã| as α, and the angle between |ã - b| and |b| as β. The law of sines states:

|ã - b| / sin(α) = |ã| / sin(β)

Rearranging the equation, we get:

sin(α) = (|ã - b| / |ã|) * sin(β)

sin(α) = (20.88 / 10) * sin(β)

Using the inverse sine function, we can find α:

α ≈ arcsin((20.88 / 10) * sin(β))

Similarly, we can find β using the equation:

β ≈ arcsin((20.88 / 14) * sin(α))

Thus, the magnitude of the vector difference is approximately 20.88, and the angles α and β can be calculated using the law of sines.

Learn more about sines here: https://brainly.com/question/16669688

#SPJ11

Answer:

you would have $160

Step-by-step explanation:

13+10+30+100+7= 160

The total amount $160 he have.

Given that,

He had amount already = $13

His mom gave him = $10

His dad give him = $30

His aunt and uncle give him = $100

He had another amount = $7

We have to determine,

How much amount he have..

According to the question,

To obtain the amount he had add all the amounts.

Therefore,

Total amount he had = He had amount already + Her mom gave him + His dad gave him + His aunt and uncle give him + He had another amount.

Total amount he had = $13+ $10+ $30+ $100 + $7

Total amount he had = $160

Hence, The required amount he had is $160.

To know more about Addition click the link given below.

https://brainly.com/question/20709440

The horizontal asymptote of function f(x) is y=6.5, which is a straight line, which means that even if time is infinite, the pH of the mouth will not rise above 6.5, which is the normal pH of the mouth.

A function's horizontal asymptote is a horizontal line with which the function's graph appears to coincide but does not actually coincide. The horizontal asymptote is used to determine the behavior of the function.

When either lim x f(x) = k or lim x - f(x) = k, the horizontal asymptote of a function y = f(x) is a line y = k. . It is commonly abbreviated as HA. In this case, k is a real number that the function approaches when x is extremely large or extremely small.However, the maximum number of asymptotes that a function can have is 2.

Given,

\(f(x)=\frac{6.5x^2-89.4x+3734}{x^2+576}\)

The horizontal asymptote of the function f(x) can be determined by

\(y=\lim_{x \to \infty} f(x)\\\\=\lim_{x \to \infty}\frac{6.5x^2-89.4x+3734}{x^2+576}\\\\=\lim_{x \to \infty}\frac{x^2(6.5-\frac{89.4}{x}+\frac{3734}{x^2})}{x^2(1+\frac{576}{x^2})}\\\\=\lim_{x \to \infty}\frac{(6.5-\frac{89.4}{x}+\frac{3734}{x^2})}{(1+\frac{576}{x^2})}\\\\=\frac{(6.5-\frac{89.4}{ \infty}+\frac{3734}{ \infty})}{(1+\frac{576}{ \infty})}\\\\=\frac{6.5-0+0}{1+0}\\\\=\frac{6.5}{1}=6.5\)

Thus, the horizontal asymptote of function f(x) is y=6.5 which is straight line which means even the time reaches infinity the pH of mouth will not increase more than 6.5, which is the normal pH of mouth.

To learn more about horizontal asymptote refer here

https://brainly.com/question/4084552

#SPJ4

Your question is incomplete, here is the complete question.

The function \(f(x)=\frac{6.5x^2-89.4x+3734}{x^2+576}\) models the pH level f(x) of a mouth x minutes after eating food containing sugar. The graph of this function is shown.

What is the equation is the horizontal asymptote associated with is function? Describe what this means in terms of mouth's pH level over time.

The gross profit made by the storekeeper is $559.872.

To calculate the gross profit, we need to determine the selling price of the merchandise and subtract the cost price.

Given:

Cost price = $672

Selling price = 83 1/3% above cost price

First, we need to find 83 1/3% of the cost price:

83 1/3% = 83.33% = 83.33/100 = 0.8333

Selling price = Cost price + (0.8333 * Cost price)

Selling price = $672 + (0.8333 * $672)

Selling price = $672 + $559.872

Selling price = $1231.872

Now we can calculate the gross profit:

Gross profit = Selling price - Cost price

Gross profit = $1231.872 - $672

Gross profit = $559.872

Therefore, the gross profit made by the storekeeper is $559.872.

To know more about cost price, visit:

https://brainly.com/question/30175345

#SPJ11

a) The amount of water in the pool after 2 hours can be calculated using the equation.

Water in pool = 10L/hour × 2 hours = 20L.

b) The pool will be 80L when the equation is satisfied: 80L = 10L/hour × Time.

Solving for Time, we find Time = 8 hours.

c) Part b) is linear.

a) To calculate the amount of water in the pool after 2 hours, we can use the equation:

Water in pool = Water filling rate × Time

Since the pool gets filled up with 10L of water per hour, we can substitute the values:

Water in pool = 10 L/hour × 2 hours = 20L

Therefore, after 2 hours, there will be 20 liters of water in the pool.

b) To determine the number of hours it takes for the pool to reach 80 liters, we can set up the equation:

Water in pool = Water filling rate × Time

We want the water in the pool to be 80 liters, so the equation becomes:

80L = 10 L/hour × Time

Dividing both sides by 10 L/hour, we get:

Time = 80L / 10 L/hour = 8 hours

Therefore, it will take 8 hours for the pool to contain 80 liters of water.

c) Part b) is linear.

The equation Water in pool = Water filling rate × Time represents a linear relationship because the amount of water in the pool increases linearly with respect to time.

Each hour, the pool fills up with a constant rate of 10 liters, leading to a proportional increase in the total volume of water in the pool.

For similar question on amount.

https://brainly.com/question/25720319  

#SPJ8

Answer:

x=5

f(x)= -5x-2

f(5)= -5(5)-2

f(5)= -25-2

f(5) = -27

Answer:

See below:

Step-by-step explanation:

So we know that \(f(x)=-5x-2\) therefore to find out what \(f(5)\) is we can insert/replace \(x\) with 5 due to it being a function, after we do that, we get this:

\(f(5)=-5(5)-2\)

Using algebra, we an find out that \(f(5)=-27\)

Cheers!

The correct answer is: Line Integral of a scalar function and Line Integral of a vector field. It  is used to integrate the derivatives in a particular plane.

According to Green's Theorem, the double integral of the vector field's curl over the area covered by the curve corresponds to the line integral of a vector field around a simple closed curve. It is mostly employed for the integration of a line and curved plane combinations. The link between a line integral and a surface integral is demonstrated by this theorem. Numerous theorems, including the Stokes and Gauss theorems, are connected to it.  This theorem may be used to change a given line integral into a surface integral, double integral, or vice versa.

In mathematical notation, Green's Theorem states:

∮C F · dr = ∬R curl(F) · dA

Where:

∮C denotes the line integral around the closed curve C,

F is a vector field,

dr is an infinitesimal vector tangent to the curve,

∬R represents the double integral over the region R enclosed by the curve C,

curl(F) is the curl of the vector field F,

dA is an infinitesimal vector element in the plane of R.

So, Green's Theorem relates the line integral of a scalar function (F · dr) and the line integral of a vector field (curl(F) · dA).

To know more about integrals:

https://brainly.com/question/29632155

#SPJ4

Answer:

(15,-14)

Step-by-step explanation:

Given that,

The midpoint of FG is (6-4) and the corrdinates of F are (-3,6).

Let (x,y) be the coordinates of point G. Using mid point formula,

\(\dfrac{x+(-3)}{2}=6\ \text{and}\ \dfrac{y+6}{2}=-4\\\\x-3=12\ \text{and}\ y+6=-8\\\\x=15,\ \text{and}\ y=-14\)

So, the coordinates of G are (15,-14).

The smallest positive integer that the intermediate value theorem guarantees a zero exists between 0 and a is 3.

What is the intermediate value theorem?

Intermediate value theorem is theorem about all possible y-value in between two known y-value.

x-intercepts

-x^2 + x + 2 = 0

x^2 - x - 2 = 0

(x + 1)(x - 2) = 0

x = -1, x = 2

y intercepts

f(0) = -x^2 + x + 2

f(0) = -0^2 + 0 + 2

f(0) = 2

(Graph attached)

From the graph we know the smallest positive integer value that the intermediate value theorem guarantees a zero exists between 0 and a is 3

For proof, the zero exists when x = 2 and f(3) = -4 < 0 and f(0) = 2 > 0.

Your question is not complete, but most probably your full questions was

Given the polynomial f(x)=− x 2 +x+2 , what is the smallest positive integer a such that the Intermediate Value Theorem guarantees a zero exists between 0 and a ?

Thus, the smallest positive integer that the intermediate value theorem guarantees a zero exists between 0 and a is 3.

Learn more about intermediate value theorem here:

brainly.com/question/28048895

#SPJ4

Adjust the parameters as needed, such as the step size (h) and the final x-value (xn), and run the code to obtain the solution for y(x).

The resulting plot will show the solution curve.

To solve the given set of differential equations using the Runge-Kutta method in MATLAB, we need to convert the second-order differential equations into a system of first-order differential equations.

Let's define new variables:

y = y(x)

z = dz/dx

Now, we have the following system of first-order differential equations:

dy/dx = z (1)

dz/dx = -k/(2y) (2)

To apply the Runge-Kutta method, we need to discretize the domain of x. Let's assume a step size h for the discretization. We'll start at x = 0 and proceed until x = infinite.

The general formula for the fourth-order Runge-Kutta method is as follows:

k₁ = h f(xn, yn, zn)

k₂ = h f(xn + h/2, yn + k₁/2, zn + l₁/2)

k₃ = h f(xn + h/2, yn + k₂/2, zn + l₂/2)

k₄ = h f(xn + h, yn + k₃, zn + l₃)

yn+1 = yn + (k₁ + 2k₂ + 2k₃ + k₄)/6

zn+1 = zn + (l₁ + 2l₂ + 2l₃ + l₄)/6

where f(x, y, z) represents the right-hand side of equations (1) and (2).

We can now write the MATLAB code to solve the differential equations using the Runge-Kutta method:

function [x, y, z] = rungeKuttaMethod()

   % Parameters

   k = 1;              % Constant k

   h = 0.01;           % Step size

   x0 = 0;             % Initial x

   xn = 10;            % Final x (adjust as needed)

   n = (xn - x0) / h;  % Number of steps

   % Initialize arrays

   x = zeros(1, n+1);

   y = zeros(1, n+1);

   z = zeros(1, n+1);

   % Initial conditions

   x(1) = x0;

   y(1) = 0;

   z(1) = 0;

   % Runge-Kutta method

   for i = 1:n

       k1 = h * f(x(i), y(i), z(i));

       l1 = h * g(x(i), y(i));

       k2 = h * f(x(i) + h/2, y(i) + k1/2, z(i) + l1/2);

       l2 = h * g(x(i) + h/2, y(i) + k1/2);

       k3 = h * f(x(i) + h/2, y(i) + k2/2, z(i) + l2/2);

       l3 = h * g(x(i) + h/2, y(i) + k2/2);

       k4 = h * f(x(i) + h, y(i) + k3, z(i) + l3);

       l4 = h * g(x(i) + h, y(i) + k3);

       y(i+1) = y(i) + (k1 + 2*k2 + 2*k3 + k4) / 6;

       z(i+1) = z(i) + (l1 + 2*l2 + 2*l3 + l4) / 6;

       x(i+1) = x(i) + h;

   end

   % Plotting

   plot(x, y);

   xlabel('x');

   ylabel('y');

   title('Solution y(x)');

end

function dydx = f(x, y, z)

   dydx = z;

end

function dzdx = g(x, y)

   dzdx = -k / (2*y);

end

% Call the function to solve the differential equations

[x, y, z] = rungeKuttaMethod();

Learn more about differential equations click;

https://brainly.com/question/32645495

#SPJ4

Answer:

5/9

Step-by-step explanation:

brainliest when possible.

Answer:

Then get 4 shorts and 5 t-shirts.

Step-by-step explanation:

^

Answer:

2

Step-by-step explanation:

1250/5 = 250/5 = 50/ 5 = 10/5 = 2

So we pulled sqrt 5, sqrt 5, sqrt 5, sqrt 5

sqrt 5 * sqrt 5 = 5 (do twice)

25 sqrt 2

The area to the right of z = -1 for the standard normal distribution is approximately 0.8413.

a. To find the area to the right of z = -1 for the standard normal distribution, we need to calculate the cumulative probability using the standard normal distribution table or a statistical calculator.

From the standard normal distribution table, the area to the left of z = -1 is 0.1587. Since we want the area to the right of z = -1, we subtract the left area from 1:

Area to the right of z = -1 = 1 - 0.1587 = 0.8413

Therefore, the area to the right of z = -1 for the standard normal distribution is approximately 0.8413.

b. To answer this question, we would need additional information about the mean and standard deviation of the annual salaries for first-year college graduates. Without this information, we cannot calculate specific probabilities or make any statistical inferences.

If we are provided with the mean (μ) and standard deviation (σ) of the annual salaries for first-year college graduates, we could use the properties of the normal distribution to calculate probabilities or make statistical conclusions. Please provide the necessary information, and I would be happy to assist you further.

Learn more about area here

https://brainly.com/question/25292087

#SPJ11

Answer:

Vertical

Step-by-step explanation:

Answer:

it is correct you are right

Answer:

whats the question?

Step-by-step explanation:

Answer:

4(9a-4)

Step-by-step explanation:

36a - 16

We can factor 4 from each expression.

4*9a - 4*4

4(9a-4)

The Egyptian mummy was buried 3023.3 years ago.

Isotopes are two or more different atom types that share the same atomic number and place in the periodic table but have different quantities of neutrons in their nuclei, resulting in various nucleon numbers.

An Egyptian mummy's burial fabric is thought to still have 59% of its original carbon-14 content.

\(t_{1/2}\)  = 5730 years

The carbon-14 time constant is:

\(t_{1/2}\) = τ × ㏑ 2

τ = \(t_{1/2}\)  ÷ ㏑ 2

τ = 5730 ÷ ㏑ 2

τ = 8266.642 years

The following is the equation for isotope mass decay:

m(t) / mₐ = \(e^{-t/\tau }\)

0.59 = \(e^{\frac{-t}{5730}\)

㏑ ( 0.59 ) = - t / 5730

t = - 5730 × ㏑ ( 0.59 )

t = - 5730 × -0.52763274208

t = 3023.3 years

Learn more about isotopes here:

brainly.com/question/14220416

#SPJ4

Answer:

-8

Step-by-step explanation:

3/4x=-18+12

x=-6×4/3

x=-8

Answer:

x = -8

Step-by-step explanation:

\( \frac{3}{4} x - 12 = - 18\)

i) multiply both sides of equation with 4

\( 4(\frac{3}{4} x - 12) = 4( - 18)\)

\((4 \times \frac{3}{4} x) + (4 \times ( - 12)) = - 72\)

\(3x - 48 = - 72\)

ii) move -48 to the right-hand side and change its sign

\(3x = - 72 + 48\)

iii) calculate the sum

\(3x = - 24\)

iv) divide both sides of equation with 3

\( \frac{3x}{3} = \frac{ - 24}{3} \)

\(x = - 8\)

The probability that a randomly selected group of 16 individuals from the campus will be selected is 0.8023 or 80.23%

Based on the sign in the elevator of the college library, the limit of 16 persons and weight limit of 2,500 pounds need to be adhered to. To ensure compliance with both limits, we need to consider both the number of people and their weight.

Assuming that the distribution of weights of individuals on campus is approximately normal with an average weight of 155 pounds and a standard deviation of 29 pounds, we can use this information to estimate the total weight of a group of 16 randomly selected individuals.

The total weight of a group of 16 individuals can be estimated as follows:

Total weight = 16 x average weight = 16 x 155 = 2480 pounds

To determine if this total weight is within the weight limit of 2,500 pounds, we need to consider the variability in the weights of the individuals. We can do this by calculating the standard deviation of the total weight using the following formula:

Standard deviation of total weight = square root of (n x variance)

where n is the sample size (16) and variance is the square of the standard deviation (29 squared).

Standard deviation of total weight = square root of (16 x 29^2) = 232.74

Using this standard deviation, we can calculate the probability that the total weight of the group of 16 individuals is less than or equal to the weight limit of 2,500 pounds:

Z-score = (2,500 - 2,480) / 232.74 = 0.86

Using a standard normal distribution table or calculator, we can find that the probability of a Z-score less than or equal to 0.86 is approximately 0.8023.

Therefore, the probability that a randomly selected group of 16 individuals from the campus will comply with both the number and weight limits in the elevator of the college library is approximately 0.8023 or 80.23%.

To know more about probability  click on below link :

https://brainly.com/question/14210034#

#SPJ11

1. In the context of spacetime, the locus of points equidistant from the origin of a spacetime plane is a hyperbola.

In Euclidean space, the distance between two points is given by the Pythagorean theorem, which only considers spatial dimensions. However, in spacetime, the concept of distance is extended to include both spatial and temporal components. The spacetime distance, also known as the interval, is given by the Minkowski metric:

ds^2 = -c^2*dt^2 + dx^2 + dy^2 + dz^2,

where c is the speed of light, dt represents the temporal component, and dx, dy, dz represent the spatial components.

To determine the locus of points equidistant from the origin, we need to find the set of points where the spacetime interval from the origin is constant. Setting ds^2 equal to a constant value, say k^2, we have:

-c^2*dt^2 + dx^2 + dy^2 + dz^2 = k^2.

If we focus on a spacetime plane where dy = dz = 0, the equation simplifies to:

-c^2*dt^2 + dx^2 = k^2.

This equation represents a hyperbola in the spacetime plane. It differs from a circle in Euclidean space due to the presence of the negative sign in front of the temporal component, which introduces a difference in the geometry.

Therefore, the locus of points equidistant from the origin in a spacetime plane is a hyperbola.

(Note: The explanation provided assumes a flat spacetime geometry described by the Minkowski metric. In the case of a curved spacetime, such as that described by general relativity, the shape of the locus of equidistant points would be more complex and depend on the specific curvature of spacetime.)

To know more about equidistant, refer here:

https://brainly.com/question/29886221#

#SPJ11

Answer:

(x-3)(x+2)

Step-by-step explanation:

¹ you open brackets.

² you put the "x" in both brackets

³ you then check for factors, that will give you a "6" when you multiply them and give you the "x" when you add or subtract them.

The statement that is the recursive definition of f is f(1) = -2 f(n) = f(n - 1) + 2  for n > 2

The function definition is given as

f(n) = -4 +2n for n > 1

Start by calculating f(2), f(3) and f(4)

So, we have

f(2) = -4 +2(2)

f(2) = 0

f(3) = -4 +2(3)

f(3) = 2

f(4) = -4 +2(4)

f(4) = 4

In the above computation, we can see that the sequence is an arithmetic sequence with a common difference of 2

So, we have

f(n) = f(n - 1) + 2

Also, we have

f(1) = -4 +2(1)

f(1) = -2

Hence, the statement that is the recursive definition of f is f(1) = -2 f(n) = f(n - 1) + 2  for n > 2

Read more about arithmetic sequence at

https://brainly.com/question/6561461

#SPJ1

Answer:

2,750+170d

Step-by-step explanation:

Calculation to Enter and simplify an expression for the amount in dollars that the company is paid

First step

Let d represent numbers of day

15(100+3d)

Second step is the Expression for the food booths

25(50+5d)

Third step is Expression for the game booths

15(100+3d)+25(50+5d)

Fourth step is the Expression for both game and food booths

15*100+15*3d+25*50+25*5d

=1,500+45d+1,250+125d

Fifth step is to make use of distributive Property

1,500+1,250+45d+125d

Last step is to make use of cumulative property

(1,500+1,250)+(45d+125d)

=2,750+170d (combine like terms)

Therefore expression for the amount in dollars that the company is paid is 2,750+170d